不等跨RC 框架的抗连续倒塌理论分析及鲁棒性评判指标研究

2022-08-01甘艺平申家旭

工程力学 2022年8期

甘艺平，喻君，陈隽，申家旭

(1. 同济大学土木工程学院，上海 200092；2. 河海大学土木与交通学院，南京 210098)

自1968 年Ronan Point 公寓倒塌以来，结构在偶然荷载(如爆炸、冲击、火灾和人为失误等)下的连续倒塌已经引起了科研学者与工程人员的广泛关注。虽然结构连续倒塌事件是小概率事件，但一旦发生后果极其严重，人员巨大伤亡以及财产重大损失均不可避免。为此，许多国家陆续出台了相关结构设计规范、规程和指南[1-3]，要求在设计过程中考虑结构的抗连续倒塌能力。

研究结构抗连续倒塌主要采用拆除构件法，即直接假设特定柱子发生失效，考察剩余结构能否跨越局部破坏却不发生倒塌的能力。近年来，众多学者采用该方法结合试验[4-9]、数值[10-13]和理论[14-19]等手段对等跨钢筋混凝土(RC)框架结构的抗连续倒塌性能进行了系统研究。揭示了结构倒塌过程可能出现的弯曲机制、压拱效应、悬梁线效应、薄膜效应以及空腹作用等荷载传递机制。随着对这些机制研究的不断深入，不同的结构抗力理论模型，如双折线模型[16]、三折线模型[17 - 18]和四折线模型[19]等也被陆续提出。

然而，上述研究主要针对等跨结构，现实中不等跨结构也十分常见，例如存在内走廊的办公楼等。最近，不等跨结构的抗连续倒塌性能开始引起了更多的关注。Du 等[20]进行了三个1/3 缩尺不等跨RC 框架的拟静力加载试验，发现板能够显著改善结构抗倒塌性能，但不等跨设计会造成短跨梁内部钢筋受力更大，从而间接弱化了结构抗连续倒塌能力。Zhong 等[21]测试了三个1/3 缩尺不等跨组合结构的抗连续倒塌性能，结果表明在大变形阶段等跨结构比不等跨结构具有更大的抗力，且不等跨结构的悬链线效应主要由短跨梁贡献。两组试验均表明了不等跨结构在倒塌过程中短跨起着主要控制作用，但该结论是在采用拟静力集中加载的前提下所得到的，而动力倒塌过程中不等跨结构是否遵循同样的破坏机制尚未明确。且适用于不等跨结构的理论分析模型也尚未有人提出。

此外，当结构存在不等跨现象时，结构的最危险工况难以直接确定。为了能快速判断出最薄弱工况，He 等[22]基于拟静力集中加载下的结构最大抗力提出了一个评判指标。然而，倒塌是一个动力过程，结构抗连续倒塌性能不仅仅依赖于抗力最大值，还受抗力形式影响。

为了解决上述不足，本文将现有等跨结构的双折线和三折线理论分析模型推广至不等跨结构，并提出了一个新的三折线模型。该模型能够同时考虑结构的抗弯、压拱、悬梁线和拉膜效应机制。基于结构最大动荷载因子提出了一个鲁棒性评判指标，用于快速确定出结构抗连续倒塌的最危险工况。

1 不等跨RC 框架结构的抗连续倒塌承载力理论分析

结构承载力理论研究一直是连续倒塌领域研究的一个重点。Dat 等[16]根据试验结果结合屈服线理论提出了结构抗倒塌承载力的双折线模型(见图1 的模型1)，但该模型忽略了结构的拉膜和悬链线效应，因此较为保守。Zhang 等[17-18]则在考虑结构在大变形下的内部能量消耗、边界水平位移等因素，利用虚功率原理求解出了结构的极限抗力，进而提出了三折线模型(见图1 的模型2)。然而，上述结构抗连续倒塌的理论分析主要还是针对等跨结构。为此，本节将进一步把等跨结构的抗连续倒塌理论拓展至不等跨结构，并提出一个新的修正三折线模型(见图1 的模型3)。

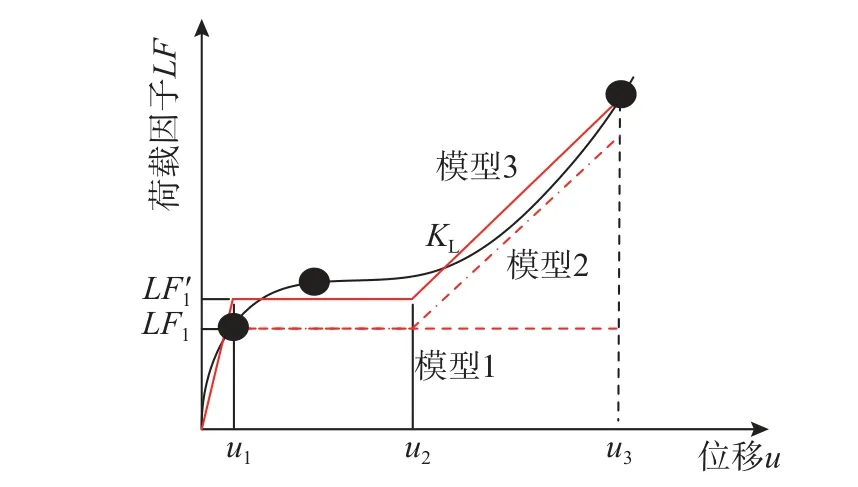
图1 结构抗连续倒塌承载力理论分析模型Fig. 1 Analytical models of progressive collapse resistance of structure

首先引入三个主要假定：1)不考虑框架整体的空腹效应，这意味着在底层和顶层失效下各单层结构的抗连续倒塌性能是一致的，类似于文献[23]，本节保守地忽略该整体效应；2)不等跨结构的最大变形位于跨中(角柱工况除外)，这是因为结构一旦发生倒塌，失效柱轴力会瞬间消失，这时失效跨内主要荷载作用为均布荷载[24]，因此假定结构最大变形发生在跨中是合理的；3)忽略梁板协同效应，即将梁和板单独计算，再进行叠加，事实上在已有的等跨结构理论中梁板协同效应中的T 型梁效应也没有被考虑，这会导致结构偏保守，但在工程领域是可接受的。

1.1 抗弯承载力

鉴于柱子位置和边界条件的差异，等跨RC 框架结构被划分成6 种典型失效工况，分别包括角柱(CC)、边邻角柱(PEC)、边中柱(SC)、对邻角柱(PIC)、邻边中柱(PSC)和内柱(IC)工况，如图2所示。

图2 RC 框架结构的6 种典型失效工况Fig. 2 Six typical column removal scenarios of RC frame structure

不等跨框架结构同样可以划分成6 种，根据前文的假定，结构在不同工况下的板屈服线和梁塑性铰分布如图3 所示。需要注意的是，在CC 工况中，除了对角正屈服线外板还会形成额外的正屈服线(OA和OB)[25]。各个工况下结构沿x向和y向的总跨长分别为Lx和Ly；dx和dy则分别代表梁沿x轴和y轴偏离跨中心的距离。板沿x向和y向的单位宽度极限抵抗负(/正)弯矩分别为和(/msx和msy)；类似地，梁沿x向和y向的极限抵抗负(/正)弯矩分别为和(/Mbx和Mby)。板和梁的极限抵抗弯矩由式(1)和式(2)求解[24]：

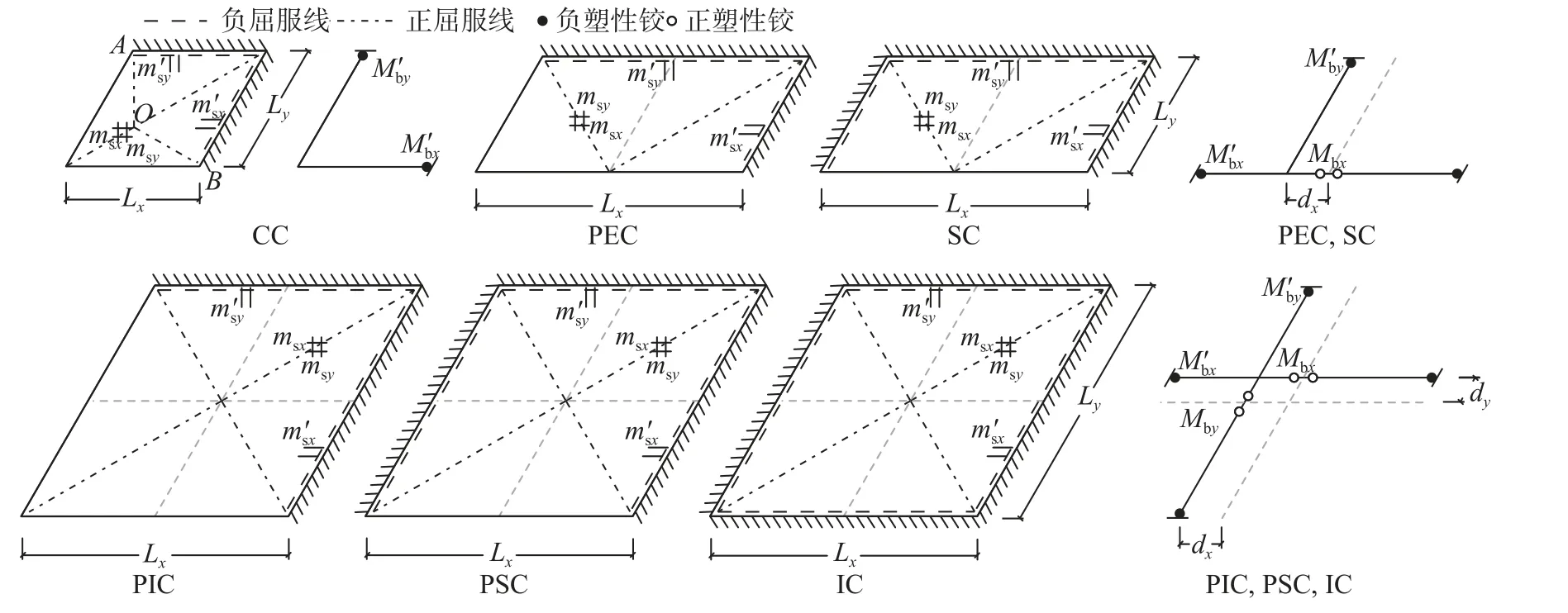
图3 不等跨结构的假定板屈服线和梁塑性铰分布Fig. 3 Assumed plastic hinges and yield-line patterns of structure with unequal spans

式中：As和Ab分别为板单位宽度和梁截面的受拉钢筋面积；hs0和hb0分别为板和梁截面有效高度；hs1和hb1分别为板和梁截面的受拉钢筋合力点到受压区混凝土中心的高度；fy和分别为钢筋屈服强度和混凝土抗压强度。

根据虚功原理，在变形最大处施加一个虚位移u，可以得到结构在外荷载下的虚功为：

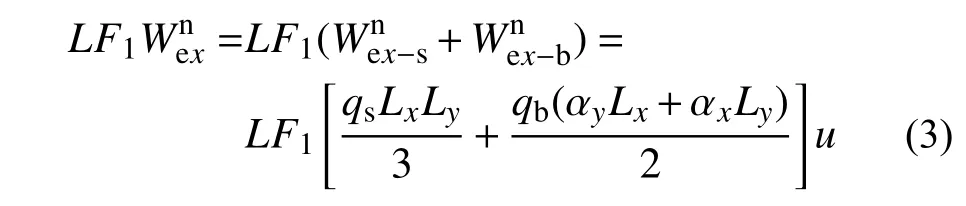
同样地，在给定的虚位移u下，通过板屈服线弯矩和梁塑性铰弯矩与相应的转角乘积，得到CC、SC 和IC 工况的内力功的表达式：

同理可得PEC、PIC 和PSC 工况下的表达式，鉴于篇幅不再列出。再根据虚功方程Win=LF1，便可解得各个工况下屈服点对应的荷载因子LF1(抗弯承载力)。

1.2 板拉伸薄膜与梁悬链线效应

结构大变形阶段主要由板的拉伸薄膜和梁的悬链线效应提供抗力。以IC 工况为例，图4 展示了结构大变形下的变形模式和受力状态。Tx和Ty分别代表x和y向板单位宽度的轴拉力；Fy和Fx则分别代表x向和y向梁的轴拉力。假设该阶段下板和梁的顶部钢筋均已屈服，结构抗力仅由钢筋贡献，但忽略底部钢筋的贡献。结构的外荷载表示成P'，该阶段下的结构抗力刚度为：

图4 板拉伸薄膜和梁悬链线效应Fig. 4 Tensile membrane and catenary action

根据力的平衡关系，荷载增量等于内力竖向分量的增量，而后者可由沿板负屈服线每个微段内的内力增量表示，因此有：

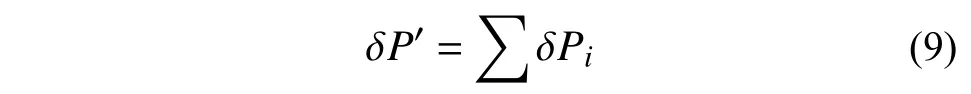
假设结构的变形曲线在负屈服线处的切线斜率近似为割线的两倍[22]，如图4 所示，从而每个微段内的内力增量可表示成：

因此，得到结构的抗力刚度表达式：

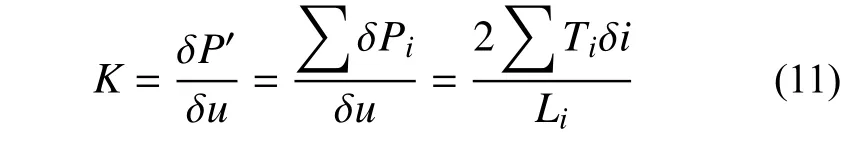
结合式(8)和式(11)则可得到结构在荷载因子坐标系下的刚度：

从而得到IC、PSC 和PC 工况的具体刚度计算公式为：

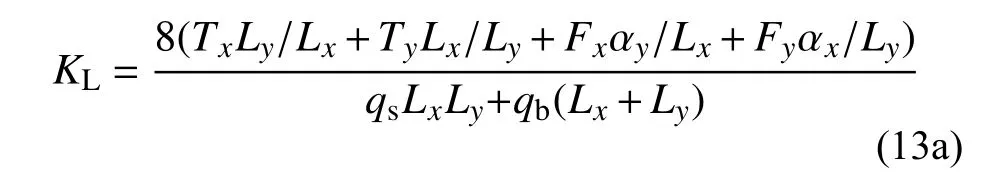
同理，可得PEC 和SC 工况计算公式：

需要注意的是，在CC 工况中，结构的变形曲线在负屈服线处的切线斜率与割线是近似相等的，故该工况下的计算公式为：

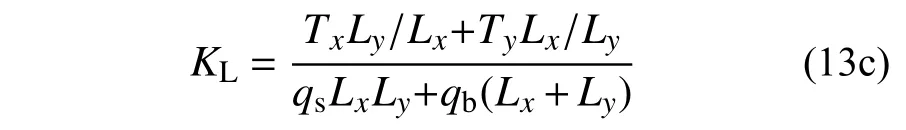
1.3 压拱效应

文献[15]表明梁的压拱效应可以提高梁承载力30%。为此，本节进一步在1.2 节所建立的三折线模型上考虑梁压拱效应的贡献。在Park 压拱模型[26]中，需要先考虑梁轴压力对截面弯矩的提高，再在宏观受力上考虑轴压力对结构抗力的不利影响。而周育泷等[15]则直接通过对梁柱构件进行实际微观受力分析，如图5 所示，提出了弯矩和轴力解耦的承载力公式。

图5 梁压拱机制下的受力模型[15]Fig. 5 Force model of beam specimen

式中，具体参数含义可参照文献[15]。α1β1fcbxc·(hb-δ-β1xc)代表梁压拱效应的贡献，将其表示成Mc。

在已有的文献[19]中，通常需要新建立一个峰值点来考虑压拱机制，即建立四折线模型。但该方法显然会导致理论公式变得更为复杂。为此，本文基于能量等效原则(即保证四折线模型和三折线模型所求得的最大荷载因子相等)对LF1进行近似修正。由式(5)～式(7)可知，LF1由梁抗弯贡献的LF1-BM和板抗弯贡献的LF1-SM组成，因此修正后的可表示成κLF1-BM加上LF1-SM。四折线模型中压拱机制峰值对应的荷载因子LF2=LF1+LF1-BC，其中梁压拱效应所贡献的LF1-BC可取0.3LF1-BM。从而根据两种模型能量相等的关系可推导出与Mc相关的修正因子表达式：

修正后结构在屈服点对应的荷载因子则可表示成：

式中，κ可取经验值1.15。修正后的三折线模型如图1 中的模型3 所示。对应的屈服点位移u1、过渡段位移u2以及失效位移u3计算公式[17-18]如下：

式中，L为失效工况下结构的等效最短梁跨长：

1.4 理论分析模型计算步骤

综上，结构在不同工况下的抗连续倒塌承载力计算步骤为：1)由式(16)和式(13)计算出屈服点荷载因子和KL；2)由式(17)和式(18)得到关键位移点u1、u2和u3；3)结合、KL、u1、u2和u3构建出修正三折线模型；4)基于Izzuddin 等[23]提出的能量平衡方法，将修正三折线模型转换成动荷载因子曲线，由式(19)求出结构最大动荷载因子。

若要保守地忽略梁的压拱效应时，可将式(16)中的κ取0，修正三折线模型(模型3)便转换成三折线模型(模型2)。当结构缺少轴向和转动约束导致无法发挥拉伸薄膜与悬链线效应时，KL取0，三折线模型则退化成双折线模型(模型1)。

2 有限元模型

有限元法是结构抗连续倒塌研究较为主流的数值方法。已有研究中RC 框架的倒塌模拟主要采用实体单元[12,27-28]和梁、壳单元[10-11,29-31]模型。实体单元虽然能全面地描述结构在倒塌下的破坏细节，但计算效率远不及梁、壳单元。为此，本文基于LS-DYNA 采用已被广泛接受的纤维梁和分层壳单元进行整体结构的倒塌分析。

2.1 不等跨RC 框架结构有限元模型

本节所建立的不等跨RC 框架结构是由一栋实际建筑简化而来，共7 层，层高均为3.6 m。x轴方向有6 跨，其中，第4 跨和第5 跨长分别为5 m和9.4 m，其余跨长7.2 m；y轴方向有3 跨，分别为7.4 m、2.6 m、7.4 m，如图6 所示。梁截面为700 mm×300 mm，配筋为上、下各4 根直径25 mm钢筋；柱梁截面为700 mm×820 mm，配筋为14 根直径25 mm 钢筋；板厚110 mm，板底和板顶均采用直径12 mm 间距200 mm 双向布筋。钢筋材料等级为HRB335，屈服强度和极限强度分别取值355 MPa 和455 MPa；混凝土材料等级为C35，抗压强度取值32.1 MPa。根据中国荷载规范[32]，结构荷载除自重外，恒载DL和活载LL分别取2.5 kN/m2和2 kN/m2，梁上施加4 kN/m 的恒载考虑墙的重量。

图6 不等跨RC 框架几何特性 /mFig. 6 Detailing of RC frame with unequal spans

在数值模型中，梁和柱采用Hughes-Liu 梁单元模拟，板采用全积分壳单元模拟，纤维梁和分层壳分别通过关键字*INTEGRATION_BEAM 和SHELL 实现，具体的纤维和层数划分如图7 所示。分层壳与纤维梁采用共节点连接，通过设置纤维梁的偏移以考虑梁板截面中心实际相对位置。梁柱的材料特性采用*MAT_PLASTICITY_COMPRESSION_TENSION 本构模型模拟，而板则选用能更好地表征双向钢筋单独受力的*MAT_CONCRETE_EC2 本构模型。结构的非线性动力倒塌分析分两步：1)在柱子移除前先通过关键字*LOAD_BODY_Z 施加荷载；2)利用关键字*MAT_ADD_EROSION 设置待移除柱的材料失效时间瞬间删除待移除柱。

图7 单元类型 /mmFig. 7 Details of elements

2.2 不等跨RC 框架结构抗连续倒塌分析

根据边界条件和梁跨度的差异，每层选取12 种分析工况(A1～A6 和B1～B6)进行分析。为考虑楼层对结构抗连续倒塌性能的影响，本文分别对1 层柱和7 层柱失效进行了探究。荷载组合采用中国倒塌规范规定[3]的1.0DL+0.5LL。结构发生连续倒塌的判断标准定义为结构最大竖向位移超过短梁跨长L的15%。

2.2.1 不同工况下的结构抗连续倒塌性能

对结构进行增量动力分析(IDA)可得到不同荷载因子(LF)下的位移时程曲线，如图8 所示。鉴于篇幅所限，只展示了A1_1、A1_7、A4_1、A4_7、B2_1 和B2_7 失效下的结构动力响应，其中Aa_b代表位于b层平面位置在Aa处的柱子。由图可知，在设计荷载(LF=1)下，无论哪种单柱失效工况均没有发生倒塌现象。A1_1、A1_7、A4_1、A4_7、B2_1 和B2_7 工况对应的破坏荷载分别为LF=1.9、2.0、2.5、2.8、3.5 和3.6，表明结构在单柱失效工况下的抗倒塌性能较好。需要得注意的是，部分工况(例如B2_7 工况)在破坏荷载下并没有发生真实的连续倒塌破坏，但其最大竖向位移已超过规定限制，即濒临倒塌的状态，因此保守地认为在该荷载下结构已发生破坏。结构能承受的极限荷载(LF=3.52)则采用通过采用破坏荷载(LF=3.5)和上一级荷载(LF=3.6)关于位移的线性插值确定。

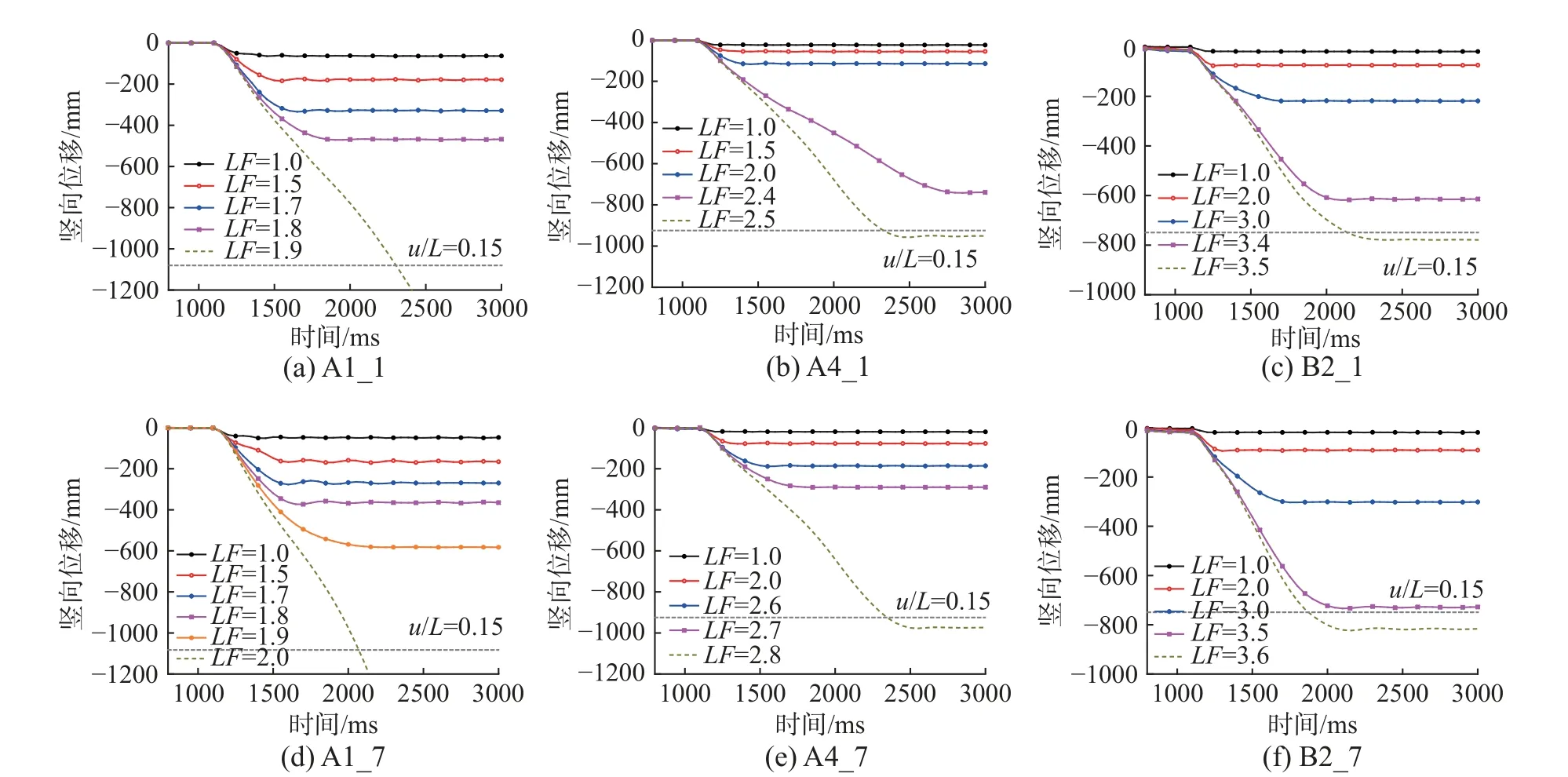
图8 不同失效工况下的结构竖向位移时程响应Fig. 8 Time history of vertical displacement of different column loss

图9 展示了1 层柱各个工况下结构的LF曲线。由图可知，结构最薄弱的工况是A6_1 工况(LFmax=1.46)，而不是角柱A1_1 工况(LFmax=1.81)。这表明并非所有结构都是角柱工况最为薄弱，还与所考虑工况的梁跨度等因素相关。对比A3_1和A5_1 工况可以发现，两者的边界条件(均为边中柱工况)和梁总跨度(14.4 m)相同，相邻跨度比为1∶1.9 的A5_1 工况LFmax比跨度比为1∶1 的A3_1 工况大了7.7%。但A4_1 工况的跨度比(1∶1.4)虽然比A5_1 小，LFmax却比A5_1 大了25.1%。这主要是因为A4_1 工况总跨度(12.2 m)比A5_1小，总跨度的减小直接引起了抗弯和压拱机制的加强。这也反映了梁总跨度的影响会比梁跨度比大。A2_1 和A3_1 工况的对比，则体现了边界条件对结构承载力的影响。A2_1 工况由于一边没有约束，导致结构的承载力与刚度均比A3_1 工况小。

图9 不同失效工况下的结构荷载因子曲线Fig. 9 Load factor from different scenarios

在内柱工况B2_1～B6_1 中，B2_1 和B3_1 是y向不等跨，B4_1～B6_1 则是x向和y向均为不等跨。由图9(b)可知，所有工况中结构承载力最大的为B4_1 工况(LFmax=4.2)，这主要是其沿x向的梁总跨度最小，这与边柱工况中的A4_1 工况一致。而梁总跨度和边界条件对其他内柱工况下结构抗倒塌性能的影响规律则与边柱工况类似。

2.2.2 不同楼层失效的结构抗连续倒塌性能

结构柱子失效不仅仅只发生于底层，如Ronan Point 建筑倒塌事件，该事件的承重构件失效便是发生于18 层。为此，本节分别对比了B4、B6、A1、B1、A4 和A6 柱在1 层和7 层失效的结构LF曲线，如图10 所示。6 种工况在1 层和7 层失效结构的初始刚度和承载力都比较接近，说明柱子失效层数对结构的抗连续倒塌性能影响较小，这也表明了本文在第一节所提的第一个假定是合理的。

图10 1 层和7 层柱失效下的荷载因子对比Fig. 10 Comprisions of load factor of 1st and 7th story column loss

边柱B1、A4 和A6 工况则是沿x均存在不等跨，且不等跨比不同。在7 层柱失效时，三种工况结构的最大响应都发生在靠近跨中位置，如图11(c)所示。但在1 层柱失效下，结构的最大变形则相对靠近失效柱。考虑到结构在1 层和7 层柱失效下的承载力比较接近，因此，作者认为本文在第一节所提的第二个假定也是成立的。

图11 不同工况下的结构竖向位移云图Fig. 11 Vertical displacement contours of structure under different scenarios

3 理论分析模型检验

本文所提出的理论分析模型采用可靠的数值模型进行检验，分别对结构最大动荷载因子和荷载因子曲线进行比较。引入相对误差的定义：

式中：LFN-i和LFA-i分别为结构抗倒塌最大动荷载因子的数值和理论结果；i为柱子失效工况。

表1 展示了不同理论模型与数值模型的结果对比。由表可知，模型1 相对误差最小和最大的分别为23.9%(A2 工况)和44.6%(B5 工况)，显然该模型预测值太过保守。而且内柱B2-B6 工况的误差率均超过了40%，远大于其他工况，这也表明了若仅考虑结构抗弯承载力将对内柱工况的真实承载力造成严重的低估。模型2 在考虑了板拉膜和梁悬梁线效应后，内柱工况的相对误差均降到了20%以内。但该模型的整体误差率还是相对较大，其中B1 工况相对误差也达到了24.7%。而在模型2 基础上考虑了压拱效应的模型3，除了A1 和B1 工况相对误差达到18%，其余工况都在13%以内，预测精度最高。因此，本文建议采用模型3 进行不等跨框架结构的最大动荷载因子计算。

表1 结构最大荷载因子的理论与数值结果对比Table 1 Comparisons of analytical and numerical maximum load factor

此外，图12 展示了采用模型3 所计算的理论结构荷载因子曲线与数值结果对比。由图可知，12 种工况结构荷载因子曲线整体趋势都符合较好，理论值略微保守，主要是因为在理论模型中保守地忽略了板压膜效应的贡献，从工程应用角度是可接受的。

4 鲁棒性评判指标

快速判断出最薄弱工况对结构的倒塌预防十分关键，但考虑到实际结构中可能存在大量的失效工况，若对每种工况均进行计算，效率十分低下。为此，本节将基于结构的最大动承载力提出一个鲁棒性评判指标，用于快速确定出结构的最危险工况。

4.1 指标提出

以IC 柱工况为例，由式(19)可知，结构的最大动荷载因子为：

支架搭设方案为系梁支架采用满堂插扣式支架，支架布置根据系梁截面位置受力情况的不同分区域进行设计。我桥采用钢管支架满布式搭设，左右幅系梁分别搭设，宽度与系梁每侧加宽1m，纵向间距0.4m，横向间距0.6m。中横梁处搭设宽度每侧加宽1m，纵向间距0.8m，横向间距0.9m。为保证稳定性，立杆沿竖向每1.35m布设横向拉杆。

式中，LF0代表双向跨度均为L0的平板结构在IC 工况下的抗弯承载力。同理可以得到各个工况下最大动荷载因子：

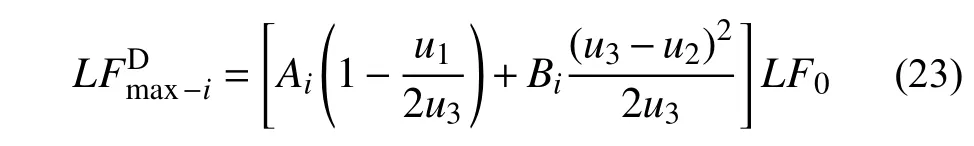
鉴于u1远小于2 倍的u3，故1-u1/(2u3)可近似等于1。将(u3-u1)2/(2u3)表示成U，根据式(17)，得到U在CC 工况下的值为0.02L，在SC 和PEC 工况下的值为0.03L，在IC、PSC 和PIC 工况下的值为0.05L。再利用LF0对各个工况下的最大荷载因子进行标准化，从而可将鲁棒性快速评判指标定义成：

考虑到A和B的表达式还太过繁琐，不便于工程应用。进一步将部分参数的建议值(κ=1.15，hs1=0.15 m，λ=hb1/hs1=4，γR=15)代入，得到A和B的简洁表达式，如表2 所示。

表2 结构鲁棒性评判指标的参数表达式Table 2 Expression of parameters for structural robustness evaluation index

4.2 指标验证

图13 展示了不同工况下结构鲁棒性快速评判指标Π 与LF的散点图。由图可知，Π 与LF呈现出非常明显的线性关系，这表明本文所提出的指标Π 可以用于对结构在不同工况下的鲁棒性进行排序，进而快速判断出结构潜在的危险工况。例如，在7 层柱失效时，Π 最小值为0.55，对应的是最危险的A6 工况(LF=1.53)。Π 相对较小的0.6和0.67 则对应了潜在的危险工况A1 和A2。

图13 结构鲁棒性快速评判指标验证Fig. 13 Load factor against the robustness index Π

4.3 敏感性分析

考虑到4.1 节为了简化公式，直接给定了参数γR、hs1和λ 的建议值，本节进一步探究这三个参数对指标Π 的敏感性。假设参数γR、hs1和λ 的取值范围分别为[10,25]、[0.12,0.18]和[3,5]，通过式(24)和表2 可计算出每个参数变化后结构的指标Π。其中，当γR变化时，hs1和λ 固定不变；hs1变化时，γR和λ 固定不变；而λ 变化时，hs1固定不变，γR则随之改变。采用Pearson 相关系数ρ 判断参数对指标Π 的敏感性。

表3 展示了γR、hs1和λ 在取上界和下界时相关系数ρ 的大小。由表可知，在建议取值下结构LF与指标Π 的相关系数高达0.99，而其他取值下相关系数ρ 也都大于0.97，展现出了极好的线性关系。这也表明了本文所提出的指标Π 十分可靠，可用于快速评判结构在不同失效工况下的鲁棒性。