轨下胶垫频变黏弹性对轨道交通箱型梁动力响应影响分析
2022-08-01左志远刘林芽秦佳良刘全民牛振宇
左志远,刘林芽,秦佳良,刘全民,牛振宇
(华东交通大学铁路环境振动与噪声教育部工程研究中心,江西南昌,330013)
轨道交通高架线路具有节约土地资源、保护环境的优势,同时可有效控制地基长期沉降,使线路具有良好的平顺性和稳定性,在已运营的高速铁路线路形式中高架桥梁占有很大比例[1-3]。当列车在高架桥梁上高速行驶时,由于轮轨不平顺激励使轮轨系统产生剧烈振动并传至轨下基础,进而引起车-轨-桥系统的振动,影响车辆、轨道、桥梁各子系统的运行质量与使用寿命,以及会给沿线居民的生活带来困扰[4-6],因此,针对轨道交通高架桥梁动力响应的精确预测及控制研究尤为必要。
目前,国内外研究人员十分重视高速铁路车-轨-桥系统振动控制,穿越敏感区域的高速铁路高架线都采取了控制措施以降低结构振动,扣件是轨道结构中重要的组成部分,兼具固定钢轨和减振的作用,其中提供减振性能的主要部件是扣件中的轨下胶垫[7]。国内外在以往车辆-轨道-桥梁系统的振动研究中,轨下胶垫的动态力学参数(刚度、阻尼)往往采用固定值[8-10]。实际上,由于轨下胶垫组分中包含橡胶高分子材料,其动态力学参数随环境条件及加载工况的变化而改变,FENANDER 等[11-16]的研究表明,橡胶高分子材料的动态力学特性具有频变黏弹性(指橡胶材料在激振频率因素影响下表现出的力学性能)。目前已有学者针对扣件的动态力学性能进行了研究,THOMPSON等[12]采用宽频试验机分析加载频率对扣件胶垫动力性能的影响,发现扣件胶垫刚度对加载频率具有明显的依赖性。MAES等[13]对扣件弹性垫板进行1~3 000 Hz 宽频激振试验,发现扣件胶垫的刚度和阻尼随频率增大而增大。刘林芽等[16]通过试验表明扣件的动态力学性能参数对频率和温度具有明显的依赖性,采用高阶分数阶导数模型能准确表征其动态力学行为。王绍华等[17]通过试验与仿真结合得出考虑钢轨扣件胶垫刚度频变特性可以更准确地预测钢轨1 阶垂向共振频率。轨下胶垫频变黏弹性会改变轨下胶垫的动态力学参数,从而影响车辆-轨道-桥梁系统的振动响应,目前,针对轨下胶垫频变黏弹性对轨道交通箱型梁动力响应影响的探讨较少。
为揭示轨下胶垫黏弹性对轨道交通箱型梁动力响应的影响规律,准确预测箱型梁的振动响应,进而为轨道交通箱型梁振动控制提供参考,本文作者提出一种考虑轨下胶垫频变黏弹性的轨道交通箱型梁动力响应联合仿真预测模型。模型以WJ-7B 型常阻力扣件的轨下胶垫为研究对象,采用FVMP 参数模型表征轨下胶垫频变黏弹性,建立考虑轨下胶垫频变黏弹性的车-轨-桥垂向耦合频域分析模型,与箱型梁三维有限元模型结合,进一步对胶垫黏弹性对轨道交通箱型梁不同输出点结构动力响应的影响进行分析。
1 基于扣件胶垫频变黏弹性车-轨-桥动力耦合理论计算方法
1.1 轨下胶垫频变黏弹性理论表征模型
轨下胶垫中参与车-轨-桥动力耦合计算的力学性能参数主要是刚度与损耗因子,为了更加清晰地描述黏弹性阻尼材料动态力学性能参数,通常需要用数学模型来近似拟合,本文选择适用于黏弹性材料宽频域拟合的高阶分数阶导数FVMP(fractional voigt and maxwell model in paralle)模型[15]来表征轨下胶垫黏弹性动态特性。
FVMP模型时域本构方程表示为
式中:Dα,Dβ和Dγ为分数阶微分算子;σ(t)为应力;ε(t)为应变;μ1和μ2为FVMP模型的弹性系数;η1和η2为FVMP模型的黏性系数;α,β和γ为分数导数阶数。
将式(1)经过变换、分离得到储能模量Es、耗能模量El与损耗因子tanδ的参数模型:
式中:ω为固有角频率。
建立的轨下胶垫的本构模型(FVMP 模型)示意图如图1所示。图中,F为施加的荷载,X为在F作用下产生的位移。
1.2 基于动柔度法车-轨-桥耦合动力分析模型
采用的车-轨-桥耦合动力学模型如图2所示。车辆系统以CRH380A动车为原型,采用单节车辆的10 自由度纵向半车模型[18],其中,Zc和θc分别为车体的沉浮、点头自由度;Zt1和θt1分别为前转向架的沉浮、点头自由度;Zt2和θt2分别为后转向架的沉浮、点头自由度;Zw1,Zw2,Zw3和Zw4分别为4个轮对的沉浮自由度。钢轨简化为Timoshenko梁,轨道板、底座板均简化为两端自由Euler-Bernoulli梁,桥梁简化为两端简支Euler梁,扣件、CA砂浆层、滑动层和桥梁支座均考虑为离散的黏弹性支承单元。
1.2.1 车辆垂向振动模型
单节车辆振动方程如下:
式中:[Mv]为车辆系统质量矩阵;[Cv]为车辆阻尼矩阵;[Kv]为车辆刚度矩阵;分别为车辆系统的位移、速度和加速度矩阵;{P}为轮轨力。
对式(5)进行变量分离可得
式中:[βw] 为车轮在轨道的轮轨接触点处动柔度矩阵,[βw]=(-ω2[Mv]+iω[Cv]+[Kv])-1;i 为虚部单位;[Zw]为轮对的垂向位移矩阵。
1.2.2 轨道-桥梁垂向耦合振动模型
轨-桥耦合系统主要包括钢轨、轨道板、底座板、箱型梁,钢轨和轨道板通过扣件连接,轨道板和底座板通过CA砂浆连接,底座板和箱型梁通过滑动层连接,箱型梁由安装在桥墩上的支座支撑。
轨-桥系统各结构层的动柔度函数表达式[19]为
式中:k1和k2分别为沿钢轨正、负方向传播的振动波;β为动柔度;φn为第n阶的振型;ωn为第n阶固有角频率;η为损耗因子;i为第i个车轮;Nc为计算模态数;下标r,s,d 和b 分别代表钢轨、轨道板、底座板、桥梁。
轨-桥系统各结构层的振动位移表达式为
式中:Z为结构位移;P为轮轨力;Nw为轮对的数量;Ff,Fj,Fz和Fq分别为扣件力、CA 砂浆离散弹簧力、滑动层离散弹簧力、桥梁支座反力;N,M和H分别为扣件、CA砂浆离散弹簧和滑动层离散弹簧的数目;n,m,h,l和w分别为扣件、CA砂浆离散弹簧、滑动层离散弹簧、桥梁支座和轮对的编号。
扣件力、CA砂浆层离散支撑力、滑动层离散支撑力、支座力可以表示为
式中:Kf为扣件复刚度;Kj为CA砂浆离散弹簧复刚度;Kz为滑动层离散弹簧复刚度;Kq为箱型梁支座弹簧复刚度,其表达式为
式中:kf和ηf分别为扣件的刚度和损耗因子;kj和ηj分别为CA 砂浆层的刚度和损耗因子;kz和ηz分别为滑动层刚度和损耗因子;kq和ηq分别为桥梁支座的刚度和损耗因子。
将式(9)代入式(8),整理可得
式中:[βK]为轨-桥系统各结构层的动柔度和复刚度相乘[20];{Z}为轨道桥梁各结构层的位移矩阵;{P}为轮轨力。
由式(11)求解轨-桥耦合系统动柔度为
式中:ZTB为轮轨力作用下轨-桥耦合系统位移;轨-桥系统动柔度,即为单位简谐荷载作用下轨-桥耦合系统位移。
1.2.3 轮轨接触模型
本文假设轮轨线性Hertz 接触。kc为接触弹簧刚度系数,则其动柔度表示为
式中:βc为轮轨接触弹簧动柔度。
1.2.4 轨道不平顺
结合德国低干扰谱(波长为1~100 m)及Sato 谱(波长为0.01~1 m)作为轨道不平顺激励[21],图3所示为高低不平顺谱。
1.2.5 求解车-轨-桥垂向耦合系统随机动力响应
基于虚拟激励法计算车-轨-桥随机动力响应,车辆与轨道的相对位置不变,轨道不平顺以车速沿钢轨移动,进而在轮轨之间产生位移激励。轮轨力的计算公式为
式中:R(ω)为轮对的虚拟激励向量。将式(14)结合式(9),(10)和(11),即可求出滑动层离散弹簧力。
2 轨下胶垫频变黏弹性对车-轨-桥系统随机动力响应的影响分析
2.1 轨下胶垫动态特性模型表征
本文选用轨下胶垫在20 ℃时的模量及损耗因子如图5所示。
为保证拟合精度,将频域离散数据采用高阶分数导数FVMP 模型的参数模型来分别进行拟合,结合遗传算法对FVMP 参数模型的参数进行识别,各模型参数见表1。为验证该模型的拟合效果,本文将轨下胶垫的频域离散动参数数据与FVMP 模型的参数模型曲线进行对比,见图4。
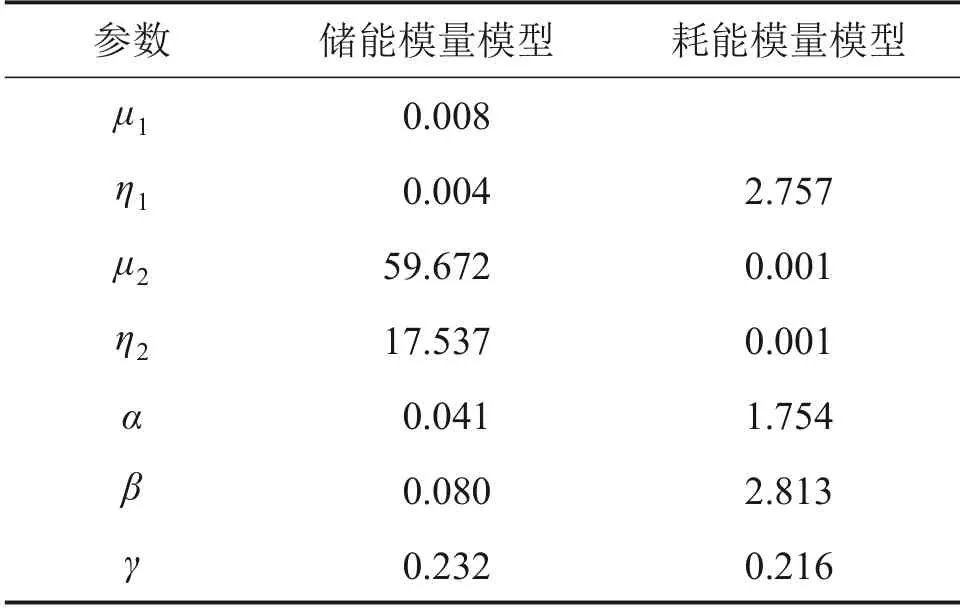
表1 轨下胶垫各模型参数Table 1 Parameter of each model of rubber pad under rail
由图4可知:轨下胶垫模量与损耗因子均随频率增大而增大,且增大幅度逐渐变缓;FVMP参数模型能够较好地描述其模量和损耗因子的频变趋势,表明FVMP 模型能够准确地反映轨下胶垫的频变黏弹性。
由于轨下胶垫中参与车辆-轨道耦合振动计算的参数是刚度、损耗因子,因此,需要将模量按照材料的结构尺寸转化为刚度,计算方法见下式[22]:
式中:kf为轨下胶垫刚度;A和h分别为扣轨下胶垫的底面积、厚度;Es为轨下胶垫储能模量。
2.2 轨下胶垫频变黏弹性对车-轨-桥耦合系统动力响应的影响分析
选用CRH380A高速列车,轨道选用CRTSⅡ型板式无砟轨道,桥梁选用32 m 简支箱型梁;为分析轨下胶垫参数(刚度和损耗因子)的频变黏弹性对车-轨-桥垂向耦合振动的影响,分4种工况进行讨论,计算工况见表2(工况中刚度与损耗因子所取定值均为20 ℃、4 Hz条件下轨下胶垫的参数[23])。

表2 计算工况Table 2 Calculated working condition
2.2.1 轨下胶垫频变黏弹性对车-轨-桥系统动柔度的影响分析
选用第一位轮轨接触点处的车-轨-桥系统动柔度为研究对象,4种工况下计算得到的车-轨-桥系统的动柔度幅值及相位分别如图5~9所示。
由图5~8可知:在4种工况下,车轮动柔度在1 Hz有峰值,该频率是车辆系统的二系悬挂频率;车轮的动柔度幅值曲线整体上随频率增大而减小;接触弹簧的动柔度取定值;轨道-桥梁动柔度在5 Hz处有峰值,该频率对应桥梁-支座系统的一阶固有频率;工况1和工况2在54 Hz处出现极小值,工况3 和工况4 在58 Hz 处出现极小值,由于车轮和轨-桥系统动柔度在对应频率点幅值相等,相位相反,导致车轮和轨-桥系统动柔度对系统总动柔度贡献量在此处部分抵消,该频率点对应车-轨-桥系统的固有频率;在[0,20)Hz频段,车轮动柔度对耦合系统的总动柔度起主导作用;对于工况1和工况2,在[20,110)Hz 频段,系统总动柔度主要由车轮、轨-桥动柔度决定,在[110,200) Hz 频段,系统总动柔度主要由轨-桥动柔度决定;对于工况3 和工况4,在[20,130) Hz 频段,系统总动柔度主要由车轮、轨-桥动柔度共同决定,在[130,200)Hz频段,轨-桥动柔度对系统总动柔度起主导作用;本文动柔度及相位的计算结果与文献[22]中结果吻合良好,验证了模型的正确性。
由图9可知:在全频段内,工况1 和工况2 的总动柔度曲线走势一致,工况3和工况4的总动柔度曲线走势一致;在[0,20)Hz 以内,4种工况下总动柔度曲线基本重合;[20,200)Hz频段,工况1~4 的动柔度幅值曲线极小值分别为1.599×10-9,1.616×10-9,1.345×10-9和1.363×10-9m/N,其极小值对应的频率分别为54,54,58和58 Hz;工况1~4 的动柔度幅值曲线极大值分别为5.580×10-8,5.281×10-8,4.300×10-8和4.052×10-8m/N,其极大值对应的频率分别为141,141,162和162 Hz,由此可知,工况3相对于工况1(或工况4相对于工况2),主要变量为轨下胶垫刚度频变,动柔度幅值曲线整体向高频移动,这是因为轨下胶垫的刚度随频率升高而升高,导致轨道结构整体刚度增大;针对较高频段内4 种工况的总动柔度幅值差异,工况2相对于工况1(或工况4相对于工况3),其主要变量为轨下胶垫损耗因子频变,由于损耗因子随频率增大而升高,导致工况2相对于工况1(或工况4相对于工况3)而言,其总动柔度曲线幅值在较高频段固有频率附近耗能明显;轨下胶垫频变对总动柔度相位的影响规律与总动柔度类似。
2.2.2 轨下胶垫参数频变特性对车-轨-桥系统随机动力响应的影响分析
采用虚拟激励法计算车速350 km/h 下车-轨-桥系统的随机动力响应。
1)垂向轮轨力。图10所示为4 种工况下计算出的动态轮轨力。
为准确分析轨下胶垫参数频变特性下的轮轨力频谱图,提取图10中曲线主峰值及对应的峰值频率,如表3所示。
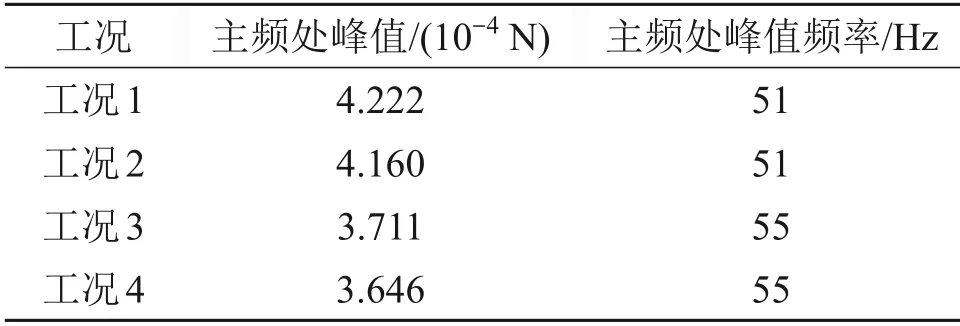
表3 轮轨力峰值及对应频率Table 3 Peak value and corresponding frequency of wheel-rail force
从图10和表3可以看出:在[0,20)Hz以下频段,4 种工况下计算的轮轨力频谱图曲线基本重合,而在[20,200) Hz 频段内的差异比较明显;工况1和工况2的轮轨力曲线基本重合,其峰值分别为4.222×104N 和4.160×104N,对应频率均为51 Hz;工况3和工况4的轮轨力曲线基本重合,其峰值分别为3.711×104N 和3.646×104N,对应频率均为55 Hz;由工况3 相对于工况1(或工况4 相对于工况2)的轮轨力频谱数据可知,在刚度频变条件下,轨下胶垫刚度随频率增大而增大,因此,轮轨力主峰值对应的峰值频率向高频偏移,进而表现出较高频段轮轨力的幅值增大;由工况2相对于工况1(或工况4相对于工况3)的轮轨力频谱数据可知,由于考虑损耗因子频变,轨下胶垫损耗因子随频率增大而增大,因此,在较高频段固有频率附近表现出轮轨力幅值曲线小幅降低。
2)滑动层等效离散弹簧力。图11所示为滑动层等效离散弹簧力。
由图11可知:轨下胶垫参数频变对滑动层等效离散弹簧力的影响规律与轮轨力的相似;4种工况下的滑动层离散弹簧力曲线在[0,20)Hz内基本重合,轨下胶垫参数频变主要影响[20,200)Hz频段范围内的滑动层等效离散弹簧力。由于刚度频变导致工况3相对于工况1(或工况4相对于工况2)的滑动层等效离散弹簧力主频向高频迁移,损耗因子频变导致在较高频段固有频率附近表现出滑动层等效离散弹簧力小幅降低。
3)桥梁振动加速度。为分析箱型梁跨中各输出点的动力响应,将滑动层离散弹簧力加载至箱型梁有限元模型顶板,如图12所示。
引入加速度振级与插入损失Ls来评价工况2,工况3 和工况4 相对于工况1 的箱型梁各输出点动力响应的影响效果,其表达式为
式中:ai为4 种工况下桥梁各输出点振动加速度;a1为工况1桥梁输出点振动加速度。
箱型梁在4种工况下不同输出点的加速度振级及插入损失,如图13~17所示。
由图13~17可知:轨下胶垫的参数频变黏弹性对箱型梁动力响应有明显影响,且箱型梁各输出点在不同工况下的动力响应规律一致,以1号输出点的动力响应为例进行分析。1号输出点4种工况的加速度振级峰值分别为117.9,117.8,116.5 和116.4 dB,对应的峰值频率分别为51,51,55 和55 Hz,工况3相对于工况1(或工况4相对于工况2)由于刚度频变导致加速度振级主频向高频迁移,工况2 相对于工况1(或工况4 相对于工况3),由于损耗因子频变导致加速度振级在峰值处有所降低。工况1与工况2、工况3与工况4的插入损失曲线在低频段内基本重合,且工况1 与工况2 仅在大于140 Hz频段两曲线出现最大0.44 dB的偏离,工况3与工况4 仅在大于140 Hz 频段两曲线出现最大0.45 dB的偏离;工况3相对于工况1(或工况4相对于工况2)在51 Hz 与57 Hz 处的插入损失绝对差值最大,最大值约为6 dB;与轨下胶垫力学性能参数(刚度、损耗因子)取定值相比,在[20,54) Hz 和[177,200)Hz 频段考虑轨下胶垫频变黏弹性会导致箱型梁动力响应偏低,在[54,137)Hz频段考虑轨下胶垫频变黏弹性会导致箱型梁动力响应偏高。
3 结论
1)轨下胶垫的频变黏弹性表现为其模量值与损耗因子均是随频率增大而增大,且增大幅度逐渐变缓;FVMP模型能够准确反映轨下胶垫的频变黏弹性。
2)轨下胶垫的参数频变特性对总动柔度及其相位有明显影响。刚度频变,总动柔度的极小值就越小,总动柔度极小值频率会向高频方向偏移,总动柔度相位在较高频段向高频迁移,这使刚度频变导致轨下胶垫储能刚度增大,轨道-桥梁系统的整体刚度也会随之变大;损耗因子频变仅会降低较高频段的固有频率附近动柔度和相位角幅值。
3)轨下胶垫参数(刚度、损耗因子)频变对接触力(轮轨力、滑动层等效离散弹簧力)的影响规律相似;轨下胶垫参数频变对在[0,20)Hz频段的接触力影响较小,轨下胶垫参数频变主要影响[20,200)Hz 频段范围内的接触力。由于刚度频变导致接触力主频向高频迁移,损耗因子频变导致在较高频段固有频率附近表现出接触力小幅降低。
4)轨下胶垫的参数频变特性对箱型梁动力响应有明显影响,且箱型梁各输出点在不同工况下的动力响应规律一致,轨下胶垫损耗因子频变导致加速度振级主频向高频迁移,轨下胶垫损耗因子频变导致加速度振级在固有频段附近有所降低;与轨下胶垫力学性能参数(刚度、损耗因子)取定值相比,考虑轨下胶垫频变黏弹性会导致箱型梁动力响应在[20,54) Hz 和[177,200) Hz 频段偏低,在[54,137)Hz频段偏高。
