循环荷载作用下扣件钢轨纵向累积位移试验研究

曾志平，胡籍，王卫东，黄相东，李平，田春雨

(1.中南大学 土木工程学院，湖南 长沙410075；2.中南大学 重载铁路工程结构教育部重点试验室，湖南 长沙410075；3.广州地铁设计研究院股份有限公司，广东 广州510010)

在铁路车站列车进站区域，列车将会进行频繁的制动作用[1-6]。在列车制动力的累积作用下，扣件与钢轨之间将会产生不可恢复的累积位移。钢轨累积位移的存在不仅使得钢轨内部产生了无法释放与恢复的应力，使得轨道结构安全性降低，同时当累积位移达到一定程度时，钢轨与轨下垫板的巨大摩擦力还会导致扣件垫板的滑移[7]，如图1所示，并对列车运营的安全性造成重大影响。在传统铁路设计中，为了简化计算，往往忽略钢轨与钢轨纵向累积位移的影响[8-10]。在传统扣件纵向阻力双线性本构中，当荷载不超过扣件滑移阻力时，卸载后钢轨会回到平衡位置，且钢轨位移与荷载曲线的加载路径与卸载路径斜率一致[11-12]。然而事实证明，在荷载反复加卸载之后，扣件会逐渐无法完全约束钢轨位移，进而产生钢轨的累积位移。因此，需要对钢轨位移的累积效应进行试验研究，探究其在不同荷载单向循环加载下，钢轨纵向位移与加载循环次数的关系，用于预测多次加卸载之后钢轨累积位移值，为相关线路设计与养护维修提供借鉴，同时也可为扣件本构关系的改进提供试验依据。

图1 循环荷载作用下扣件垫板滑移现象Fig.1 Slip phenomenon of fastener pad under cyclic load

1 试验原理

根据规范《高速铁路扣件系统试验方法第1部分：钢轨纵向阻力的测定》(TB∕T 3396.1—2015)[13]，进行扣件纵向阻力与钢轨累积位移测试。

试验采用DH3822便携式动态信号测试分析系统采集数据，采样频率为50 Hz。测试时，计算机通过以太网接口和4 G网络(WiFi可选)与仪器通讯，对采集器进行参数设置(量程、传感器灵敏度等)、清零、采样、停止等操作，并实时传送采样数据。采用轮辐式力传感器测量加载设备(千斤顶)作用在钢轨上的拉力大小，其型号为NOS-F301，量程30 kN。同时采用位移传感器测量钢轨与轨枕间的相对位移，其型号为YWC-10，量程0～10 mm，灵敏度0.340 mV/mm。

1.1 扣件纵向阻力的测定

在进行扣件纵向阻力测试时，按标准组装状态用扣件将钢轨固定在轨枕上，对钢轨轨底的中心线施加荷载，在钢轨断面中心位置布置一个位移传感器测定钢轨的纵向位移(位移传感器固定在轨枕上)，试验工装示意图如图2所示。试验加载时，以10 kN/min的恒定加载速率向钢轨施加拉力，同时测量荷载及钢轨相对扣件的纵向位移。当钢轨出现滑移，迅速将荷载卸载到0并连续测定钢轨位移2 min。每次施加的间隔时间为3 s。

图2 试验工装示意图Fig.2 Schematic diagram of test tooling

1.2 钢轨累积位移的测定

在进行钢轨累积位移加载时，采用千斤顶通过信号传输线与继电器装置连接，通过继电器装置上的控制器调整继电装置的加载时间，每隔38 s进行一次加载，每次加载持续时间为2 s，目的在于模拟列车每隔38 s经过一次，每次持续时间为2 s。在一次模拟受力后，千斤顶卸力并等待38 s，然后再次施加力度，时间为2 s，以此重复。

2 钢轨纵向累积位移

2.1 钢轨纵向位移−荷载关系分析

对弹条Ⅲ型分开式扣件进行纵向阻力测试，试验重复进行4次，将第1次加载的值弃用，后3次加载的试验结果取平均值作为钢轨纵向阻力值。试验得到的扣件纵向阻力−位移曲线如图3所示。

由图3知，弹条Ⅲ型分开式扣件纵向极限阻力为8.8 kN，弹塑性界限为0.339 mm。按照传统双线性扣件本构，当扣件节点处的钢轨与轨枕纵向位移小于0.339 mm时，荷载与位移应呈线性关系，当位移大于0.339 mm时，随位移增大荷载应一直保持在极限阻力8.8 kN，当荷载卸载时，卸载路径斜率应与加载时相同[14-15]。但是事实证明，传统本构模型与实际情况明显不符。

通过试验可见，在荷载未达到极限阻力前，扣件的纵向刚度(荷载−位移曲线的斜率)并不是保持不变的，而是逐渐变缓，在卸载过程中，曲线也并没有按照原来的路径返回，因此对扣件施加小于极限阻力的单向循环荷载，并进行钢轨残余位移的试验验证，具有深远的研究意义。

2.2 残余位移-加载次数关系分析

为研究钢轨在大量列车荷载作用下的纵向位移能否满足限值要求，特以配套2组扣件的钢轨系统为对象，扣件类型为弹条Ⅲ型弹性扣件，进行作用次数超过1万次的重复加卸载试验，获取扣件在大量重复纵向荷载下的纵向累积位移，并在重复加载前后分别测试并对比分析扣件的纵向阻力-位移特性，探明大量纵向重复荷载作用下扣件纵向阻力性能变化规律，得出钢轨累积位移与加载次数的关系，最终用于预测大量列车循环加载后钢轨累积位移值。

根据试验结果绘制扣件在第1次、第57次、第345次、第403次、第461次、第518次、第576次、第633次、第691次、第806次、第1 209次、第1 267次、第1 382次、第2 764次、第4 147次、第5 529次、第6 912次、第8 294次、第9 676次、第11 059次以及第12 441次加载时的荷载位移曲线(图4)，并提取对应加载次数下钢轨的纵向残余位移，绘制扣件残余位移-加载次数曲线图(图5)。

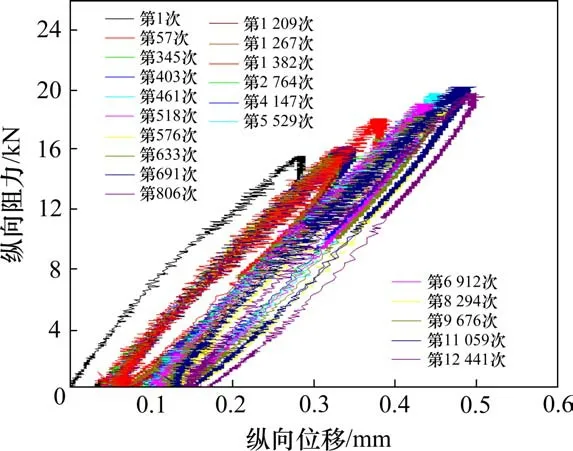
图4 重复加载下扣件纵向位移Fig.4 Longitudinal displacement of the fastener under repeated loading

图5 残余位移随荷载作用次数变化关系Fig.5 Relationship between cumulative displacement and the number of load actions

由于本次重复加载试验施加最大荷载值为20 kN，小于扣件最大纵向阻力，加载时扣件始终处于弹性变形阶段，故扣件残余位移和纵向最大累积位移数值均较小。

由图4可知，在同一次循环加载下，扣件纵向位移随荷载值的增大而增大，且两者近似为线性变化关系；随着循环荷载次数的增加，相同大小的纵向加载力下扣件纵向位移最大值逐渐增大。钢轨位移的增长速率(位移-荷载曲线的斜率)在循环次数较小时增长较快，循环次数增大后位移增长速度逐渐变缓。

由图5可知，在未达到扣件极限阻力前，钢轨的累积效应仍旧存在，在经过大量重复加载后钢轨纵向残余位移的增长速率有所减小，但钢轨残余位移将会进一步增大。

2.3 钢轨纵向残余位移拟合分析

不同循环次数下钢轨纵向残余位移值如表1所示，可见：钢轨位移随荷载循环加载次数的增大而增大，其中第1次加载时，钢轨纵向残余位移值为0.030 8 mm；第57次加载时，钢轨纵向残余位移值为0.061 9 mm；直至第12 441次加载时，钢轨纵向残余位移值达到0.162 0 mm，最大纵向位移值为0.497 mm(荷载作用值为20 kN)。

表1 不同循环次数下钢轨纵向残余位移Table 1 Longitudinal cumulative displacement of fastener under different cycles

在整个试验期间扣件加载时最大纵向位移值和残余位移值均较小，在现有的加载次数下钢轨位移值并不会超限。而在实际工程中，荷载作用次数将随着运营时间的增加而不断累积，为了获得长期作用下扣件纵向位移的变化规律，特对试验数据进行拟合，得到钢轨纵向残余位移f(x)和循环次数x间的函数关系如式(1)所示：

f(x)=0.017 58x0.2332(1)

进而获得较大重复次数下钢轨纵向位移值。该公式拟合系数为0.935 1，拟合度较高，具有一定的可信度。拟合曲线如图6所示。

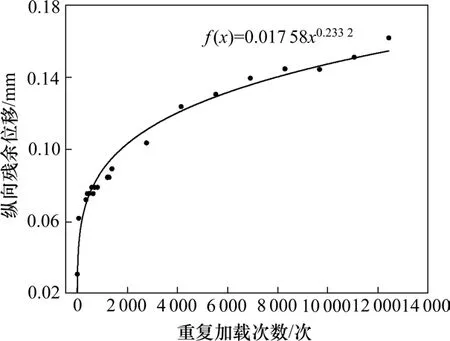
图6 钢轨纵向残余位移-循环次数拟合曲线Fig.6 Fitting curve of the longitudinal cumulative displacement of the rail-the number of cycles

由拟合曲线可知，在经过大量重复加载后钢轨纵向残余位移的增长速率虽有所减小，但钢轨残余位移值仍会进一步增大。

2.4 基于拟合公式的钢轨累积位移值推算

根据该拟合公式推算出钢轨在经历2万次、2.5万次、5万次、10万次、20万次、40万次和80万次纵向荷载重复作用后的纵向残余位移值(如表2)，并联合试验数据绘制钢轨残余位移-加载次数曲线图(如图7)，用于预测大量列车循环加载后钢轨累积位移值。

由表2和图7可知：荷载循环加载次数为2万次时，钢轨纵向残余位移为0.177 0 mm，纵向位移随循环次数的增加而缓慢增大，当循环次数增至80万次时，扣件残余位移达到0.418 4 mm，在经过大量重复加载后钢轨残余位移值仍旧有进一步增大的趋势。

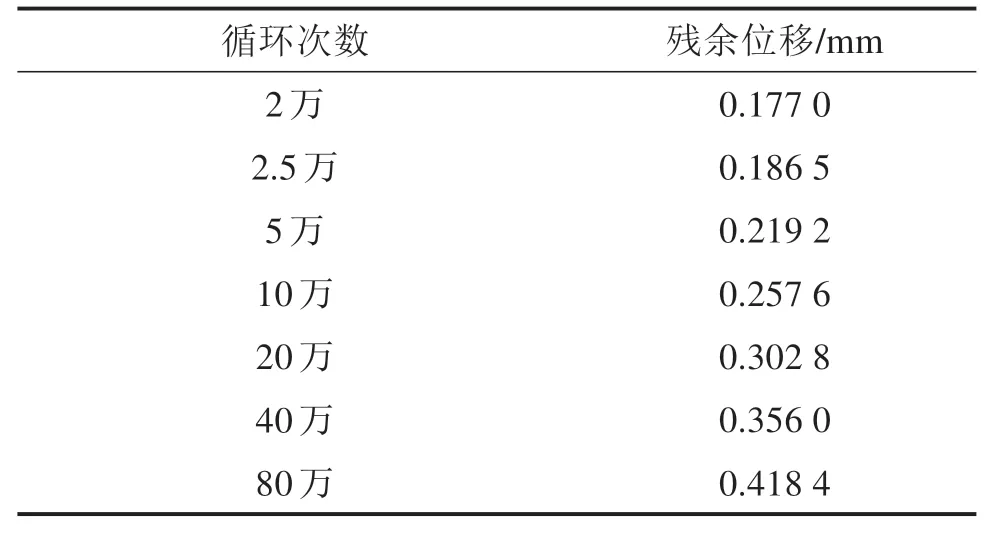
表2 不同循环次数下钢轨残余位移Table 2 Cumulative displacement of the rail under different cycles

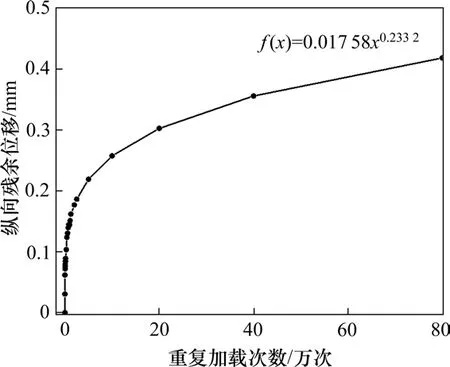
图7 重复加载下钢轨纵向残余位移−循环次数曲线Fig.7 Curve of longitudinal cumulative displacement of rail at fastener under repeated loading vs.cycle number

3 重复荷载后钢轨加载分析

3.1 重复荷载对扣件纵向阻力的影响

由图4可知，在多次重复加载后，扣件最大纵向阻力等参数已经发生了变化。因此，为更全面地研究多次重复荷载加载后再对扣件进行加载时的钢轨位移情况，需要考虑大量重复加载作用后对扣件纵向阻力-钢轨位移特性曲线的影响，获得扣件纵向刚度等参数已经发生变化情况下，纵向荷载作用瞬间钢轨的最大纵向位移。

为研究荷载重复作用对扣件纵向刚度与纵向阻力等参数的影响，特在扣件重复加载试验开始和结束时测试扣件纵向阻力，分别测试4次，舍去第1次试验结果，将后3次取均值后得扣件纵向阻力，并将2组试验数据绘制成图，如图8。

由图8可知，在经过12 441次重复加载后，扣件刚度、扣件最大纵向阻力和滑移阻力均有所增大，弹性位移有所减小。

图8 重复荷载前后扣件纵向阻力−位移特性Fig.8 Longitudinal resistance-displacement characteristics of fastener before and after repeated loading

试验加载前，扣件最大纵向阻力为23.11 kN，扣件滑移阻力为21.99 kN，弹塑性界限位移为0.493 3 mm；试验加载后，扣件最大纵向阻力为24.30 kN，扣件滑移阻力为23.22 kN，弹塑性界限位移为0.469 6 mm。扣件最大纵向阻力相比增大了5.15%，扣件滑移阻力相比增大了5.59%，弹塑性界限位移相比减少了4.80%。

从上述分析可知，纵向荷载重复作用后扣件纵向刚度(加载时曲线的斜率)、扣件最大纵向阻力和扣件滑移阻力同样会有所增大，扣件弹塑性界限位移将会有所减小，但最大弹性阻力却有所上升。

3.2 重复荷载后钢轨纵向位移加载分析

由于试验加载时纵向荷载最大值为20 kN，小于试验加载前扣件最大纵向阻力和滑移阻力，可知扣件在整个试验期间以及80万次重复加载中将始终处于弹性阶段，为简化计算，假设扣件刚度不变，根据2.3节的拟合公式结合扣件刚度算出纵向荷载为20 kN时，2万次、2.5万次、5万次、10万次、20万次、40万次和80万次循环次数下扣件的最大纵向位移(表3)，可见扣件在经过80万次循环加卸载后，加载时钢轨纵向位移最大值为0.753 4 mm，通过对比不同地段钢轨最大纵向位移的限值，可以判断多次重复荷载后加载瞬间钢轨纵向位移是否超限。

表3 重复荷载后钢轨加载时纵向位移值Table 3 Longitudinal displacement values of rails after repeated loading

4 结论

1)在未达到扣件极限阻力前，钢轨的累积效应仍旧存在，且钢轨累积位移随着荷载作用次数的增大有进一步增大的趋势。

2)对于弹条Ⅲ型分开式扣件，钢轨纵向残余位移f(x)和循环次数x间的函数关系近似满足幂函数形式：f(x)=0.017 58x0.2332，且拟合度较高(R2=0.935 1)，具有一定的可信度，可以用于预测获得不同重复荷载作用后钢轨纵向累积位移值。

3)经过大量纵向荷载重复作用后，扣件纵向刚度、扣件最大纵向阻力和扣件滑移阻力会有所增大，扣件弹塑性界限位移将会有所减小。

4)通过拟合公式可以计算出不同循环次数下钢轨残余位移，同时结合扣件纵向刚度可以计算出加载时钢轨最大纵向位移，通过对比不同地段钢轨最大纵向位移的限值，可以判断多次重复荷载后加载瞬间钢轨纵向位移是否超限。

5)该研究成果可以用于预测多次加卸载之后钢轨累积位移值，为相关线路设计与养护维修提供借鉴，同时也可为扣件本构关系的改进提供试验依据。