地铁轨道扣件和减振垫参数的减振性能最优匹配

张皓迪，何远鹏，王星欢，姜晓文，圣小珍

(1.西南交通大学牵引动力国家重点实验室，四川成都，610036；2.深圳市城市交通规划设计研究中心股份有限公司，广东深圳，518057；3.上海工程技术大学城市轨道交通学院，上海，201620)

截至2019年底，我国已有6 736 km 城市轨道交通线路投入运行，其中地铁5 181 km，占比77%。地铁作为一种高效而主要的交通方式，近年来一直发展迅猛。当地铁穿行于密集的市中心区域时，其引起的振动通过隧道、土壤传递，进而诱发上层结构的环境振动及二次噪声问题，给沿线居民的生活带来了极大的困扰[1]。

为降低环境振动带来的损害，可采用分级减振的方法进行减振，常用的分级减振方法可分为对振源、传播路径及受振结构上进行的减振[2]。目前，最为常用的振源减振措施为减振扣件与轨道板下减振垫[3]。减振扣件主要通过改善轮轨相互作用力，降低P2 轮轨共振力的幅值和频率来降低环境振动。同时，由于减振扣件成本低，便于维护，工程中应用广泛。而减振垫主要是与轨道板及其上部结构形成隔振系统对环境振动进行控制。与减振扣件相比，减振垫减振效果明显，但施工难度大，常常作为中-高级减振措施，在工程中也得到较为广泛的应用[4]。

为达到最佳的减振效果，工程中常常需要同时使用多级减振措施，而相互间的匹配问题就变得尤为重要。为此，韦凯等[5]研究了扣件胶垫对隧道环境振动的影响，冯青松等[6]研究了扣件刚度对隧道结构振动的影响，蒋吉清等[7]研究了剪力铰的引入对浮置板轨道结构振动的影响。针对多级减振措施，吴天行[8]研究了单一参数的扣件和浮置板的组合减振效果；陈代秀等[9]研究了轨下减振垫与枕下减振垫的组合对轨道振动的影响；和振兴等[10]研究了扣件与减振垫分别对轨道结构振动的影响。目前，国内学者对于减振措施的匹配的研究主要局限于针对单一轨道结构、隔振措施、轮轨力、轨道振动等，并没有基于环境振动评价指标对常规的减振垫与扣件进行耦合匹配，难以给工程中减振垫和扣件的选型提供参考。

基于以上原因，本文作者主要针对工程中最为常用的2种措施(减振扣件和减振垫)的最优匹配进行研究。该研究结果可为减振垫及减振扣件的工程运用提供参考。

1 环境振动模型的建立

对于地铁环境振动预测模型，可分解为车辆-轨道系统和隧道-大地系统2 个子系统，采用垂向轮轨相互作用模型[11]模拟车辆-轨道系统，采用2.5维有限元-边界元法[12]对隧道-大地系统进行模拟，并考虑2个子系统之间的相互耦合[13]。

1.1 车辆模型

采用瞿婉明[14]提出的多刚体半车模型，每节车包含半个车体、2 个1/2 转向架、4 个1/2 轮对以及一二系悬挂。列车的振动微分方程为

式中：Mvh为列车质量矩阵；Cvh为列车阻尼矩阵；Kvh为列车刚度矩阵；Qvh(t)为列车等效载荷向量；uvh(t)为列车位移向量；(t)为列车速度向量；(t)为列车加速度向量。

1.2 轨道模型

轨道系统从上至下依次为钢轨、轨道扣件、轨道板、减振垫和底座板。钢轨与轨道板模拟为连续支撑的欧拉梁模型，扣件与减振垫考虑为阻尼弹簧，底座板考虑为刚性。在模型中，单个扣件的刚度除以枕跨0.625 m，得到每延米的刚度作为计算值。

轨道方程在波数域有如下形式：

式中：kf为扣件刚度；kp为减振垫刚度；ErIr为钢轨的弯曲刚度；EsIs为轨道板的弯曲刚度；mr为钢轨的质量；ms为轨道板的质量；wr为钢轨的垂向位移；ws为轨道板的垂向位移；β为波数；ω为角频率；Fr为轮轨力。

1.3 轮轨相互作用模型

轮轨之间的动态相互作用力是系统的激励源，对于200 Hz 以内的轮轨系统的振动，轨道垂向长波不平顺引起的振动占主导地位[11]。采用SHENG等[11]提出的基于轨道垂向不平顺的垂向激励模型，通过该模型进行计算得到轮轨系统对应于不同波长的单位粗糙度下的轮轨力响应，再结合轨道不平顺功率谱，即可得到系统的输入激励。

轮轨耦合模型如图1所示。轮对与钢轨之间为赫兹接触，假设轮对与钢轨不发生分离，可得轮轨之间位移匹配方程[11]为

式中：为钢轨上第l和k个轮轨接触点之间的位移频率响应函数，可通过对式(2)进行傅里叶逆变换进行计算；为车辆中第l和k个轮对之间的位移频率响应函数，可通过列车系统的柔度矩阵进行计算；N为轮轨总数；kHi为轮轨接触刚度；(Ω)为粗糙度幅值；(Ω)为轮轨力幅值。已知粗糙度幅值(Ω)可计算得到轮轨力幅值(Ω)。

1.4 隧道-大地2.5维边界元-有限元模型

由于隧道-大地结构在轨道方向无限长，且横截面大，如果用三维数值模型对其进行计算会消耗大量的算力。2.5维有限元-边界元法充分考虑了无限长结构的特点，通过傅里叶变换对长度方向的坐标进行波数离散，只需要在截面上进行网格划分，并计算每一个波数对应的响应，再通过傅里叶逆变换就可以得到实际的响应。相较于三维模型，大大提高了计算效率。

根据2.5维有限元法的理论，系统的有限元方程有如下形式[12]：

式中：K0，K1和K2为系统的相关刚度矩阵；i为虚部单位；M为系统的质量矩阵；(β)为位移向量；(β)为荷载向量。

根据2.5维边界元法的理论，系统的边界元方程有如下形式[12]：

式中：H和G为弹性体的系统矩阵；(β) 为位移向量；(β)为面力向量；(β)为作用在弹性体上的体力的贡献值。2.5 维边界元与2.5 维有限元，2.5 维边界元与2.5 维边界元的耦合结果已由SHENG等[12]推导得到。

2 模型验证

2.1 实验介绍

深圳地铁一号线建成早，工作强度大，运营时间长，扣件老化明显。测试选取的线路段为盾构普通隧道，在该区间内列车运行速度为70 km/h。为得到线路的不平顺状态并与仿真进行对比，需要测试该线路的轨道不平顺性，以及列车运行情况下的隧道壁加速度振级。

源强的测试按照GB/T 19846—2005 进行，测试点选取在隧道壁上，距轨面高1.2 m处。测试采用B&K 振动测试数据采集系统，型号为3560D，隧道壁上安装B&K 公司加速度传感器，量程为7g。测试隧道的断面以及隧道壁上加速度计的布设如图2所示。

轨道不平顺性通过CAT 轨道不平顺测试仪进行测量。由于测试仪器的限制，测量的长波不平顺的波长只能达到2 m，对应70 km/h 的车速只能覆盖到9.7 Hz以上的轮轨激励频率，能较好地覆盖环境振动的主要频率[11]。但本文研究的频率范围为80 Hz以下，因此，需要补充长波段的不平顺功率谱。图3(a)所示为本文实测粗糙度与美国5 级谱、美国6级谱、德国高干扰谱与德国低干扰谱[14]的对比。由图3(a)可以看出：该线路的不平顺水平与美国5级谱相似。因此，在联合粗糙度谱时，为保证谱线随频率变化是连续的，在实测谱与美国5级谱的交点处进行拼接，短波段选取实测粗糙度，长波段用美国5级谱进行补充，得到的联合不平顺功率谱如图3(b)所示。

2.2 预测与测试的对比

根据当地地勘报告及设计图纸，可得土层以及隧道结构的参数如表1所示。其中隧道内外直径分别为5.4 m和6.0 m，埋深为17 m。

表1 隧道-土体模型参数Table 1 Parameters of tunnel-ground model

隧道-大地模型如图4所示。层状大地结构采用2.5维边界元进行模拟，单元长度为0.5 m，土层的截断宽度为30 m(边际距隧道中心线的距离)，并在大地的截断处按指数衰减[12]。

该隧道结构为普通整体道床结构，轨道模型参数如表2所示。列车模型为A型地铁列车，运行时速为70 km/h，其他参数如表3所示。

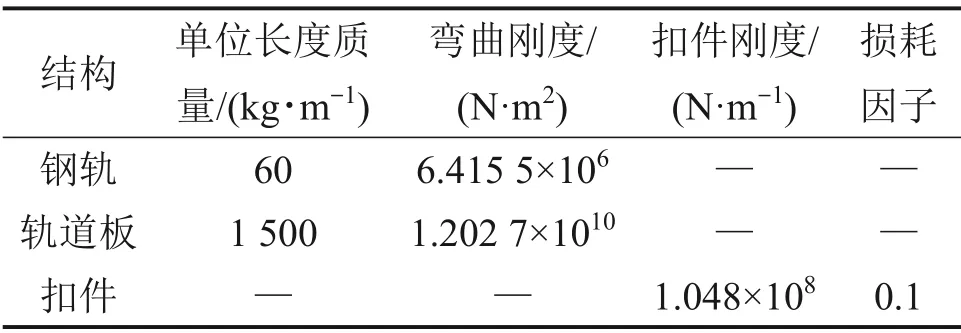
表2 轨道模型参数Table 2 Parameters of track model

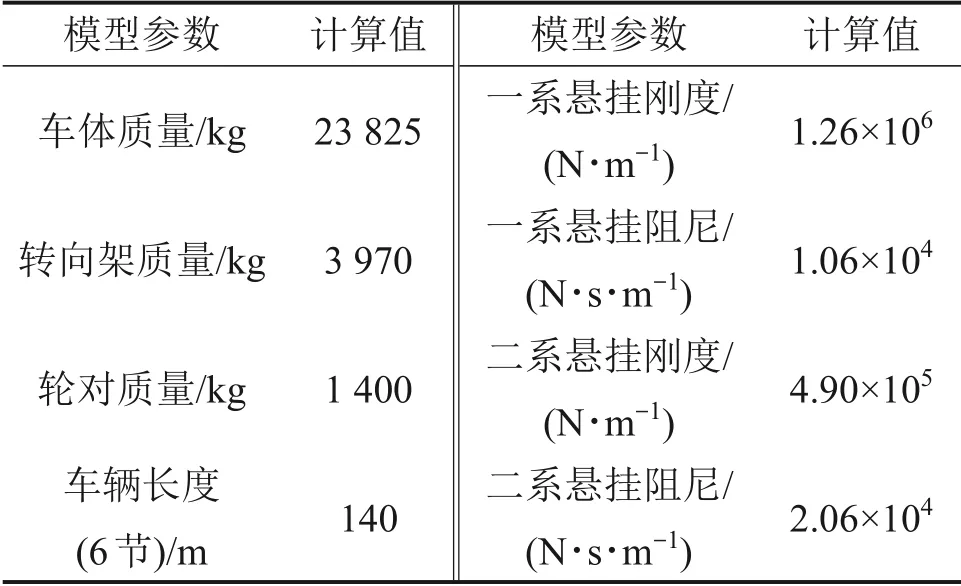
表3 A型车模型参数Table 3 Parameters of A-type vehicle model

将上述参数代入环境振动预测模型中计算，得到1/3倍频程的振动加速度级与实验测得的振动频谱对比如图5所示。

由图5可知：隧道壁的振动加速度级在8～80 Hz 内随频率增大而增加，在80 Hz 处取得极大值。当频率高于80 Hz时，振动加速度级随频率增加而降低。根据文献[15]，80 Hz 处的振动峰值频率与本文轮轨耦合共振频率吻合。通过数值模拟与实验对比，可以看出在8～200 Hz 内与测试值的趋势及幅值吻合较好，即该模型能很好地反映实际情况。

由于实际结构很复杂，例如模型未考虑轨道扣件、轨道板的周期性，实际隧道壁是管片结构而不是连续结构，材料参数也存在一定不确定性，导致80 Hz 以上的高频段预测与测试值有较大差别。但总体来说，预测结果是令人满意的。

由于该地铁区段运营时间长，扣件老化明显，环境振动及二次噪声严重超标，故需要考虑多级减振措施对该区段的振动与噪声进行控制。

3 参数调查

3.1 工况介绍

减振垫的隔振频率定义为单位长度上，轨道上部结构质量在减振垫上振动的固有频率，可由下式计算得到：

式中：k为减振垫每延米的刚度；m为上部结构(轨道板与钢轨)每延米的质量。

根据文献[16-18]可知，扣件垂向刚度为20～60 kN/mm，减振垫隔振频率为8～30 Hz。故本文扣件刚度选取10，20，30，40，50 和60 kN/mm 共6种；考虑扣件的损耗因子为0.1 和0.3 这2 种情况。减振垫以隔振频率为参数，选取隔振频率为8，14，20，30，35，50，70 和85 Hz 与无隔振(刚性连接)，共9 种，减振垫的损耗因子考虑为0.4。组合得到108组工况。

3.2 结果分析

为了研究扣件刚度和减振垫隔振频率相互耦合对减振效果的影响规律和影响机理，主要从轮轨力、隧道壁的1/3倍频程中心频率上的振级和隧道壁Z振级展开研究。

3.2.1 参数匹配对轮轨力频谱的影响

图6所示为扣件刚度对轮轨力频谱的影响(无隔振措施，扣件损耗因子为0.1)。

由图6可知：轮轨力的主要频率成分集中在P2轮轨共振力处，P2力的频率主要由扣件刚度决定，且随扣件刚度变大而增高：10，20，30，40，50和60 kN/mm 的扣件对应的P2 力频率依次为36，44，50，56，60 和66 Hz。

图7所示为减振垫隔振频率对轮轨力频谱的影响(扣件刚度为40 kN/mm，扣件损耗因子为0.1)。

由图7可知：减振垫的隔振频率对轮轨力峰值频率的影响较小。

图8所示为扣件损耗因子对轮轨力频谱的影响(扣件刚度为40 kN/mm，无隔振措施)。

由图8可知：增加阻尼会有效降低轮轨共振峰值附近的轮轨力，而对峰值频率影响较小。

3.2.2 扣件、减振垫参数对隧道壁分频振级的影响

扣件、减振垫参数的改变会引起轮轨力峰值频率与峰值大小的改变，接着影响隧道壁振动的各频率成分。图9所示为减振垫与扣件刚度对隧道壁的分频加速度振级的影响。

由图9可知：隧道壁的振动随频率增加整体呈增大的趋势，在25～80 Hz 频率范围内，存在局部最大值；随扣件刚度增加，隧道壁振动的局部峰值往高频移动，结合图7可知，该峰值频率与轮轨耦合共振频率一致；减振垫的工作频率为隔振频率的倍。高于工作频率的振动级会被缩小，而低于工作频率的振动级则会被放大。隔振频率越低，减振效果越明显。

图10所示为扣件损耗因子对隧道壁分频振级的影响。扣件刚度选取10 kN/mm与30 kN/mm这2种情况，减振垫选取隔振频率为8 Hz 与无隔振措施2种情况。

由图10可知：在环境振动评价的频率范围内(80 Hz 以下)，扣件阻尼增大只影响轮轨共振力频率附近的隧道壁振动峰值，而对其他频率成分影响较小。

为进一步说明扣件、减振垫参数对隧道壁Z振级的作用机理，图11在图9的基础上对隧道壁分频振级按Z振级的权重进行计权，反映不同频率对于Z振级的贡献，其中扣件损耗因子为0.1。

由图11可以看出：对于不同的扣件刚度，计权后对Z 振级起主要贡献的振动级频率仍然在P2力峰值频率附近；由于Z计权在低频权重高而高频权重低，因此，采用刚度较大的轨道扣件能使振动级峰值频率升高，而导致振动级峰值处的权重降低或振动级峰值移出计权频率范围，从而降低Z振级。采用隔振频率较低的减振垫，虽然能使低频振动级增大，但能显著降低峰值频率的振动级，进而降低Z振级。

3.2.3 参数匹配对隧道壁Z振级的影响

图12所示为扣件损耗因子为0.1 和0.3 的情况下，隧道壁Z振级随扣件、减振垫刚度变化的等高线图。该图利用本文调查的耦合工况计算结果，并对其采用双调和样条插值获得。

黑色等高线的值为在无隔振情况下，扣件为地铁中常用扣件(DT-III扣件，垂向刚度为40 kN/mm)的隧道壁Z振级，基于此，红色与绿色的等高线分别代表对应于DT-III扣件插入损失为5 dB与10 dB的分界线，根据GB 50157—2013[19]，减振措施根据插入损失大小可分为一般减振措施(0，5]dB、中等减振措施(5，10]dB、高等减振措施(10，15]dB。

从图12(a)可知：在扣件与减振垫匹配中，Z振级存在局部最大值和最小值，最大值出现在20 kN/mm 的扣件与85 Hz 隔振频率的减振垫匹配处，最小值出现在60 kN/mm的扣件与8 Hz隔振频率的减振垫匹配处。减振垫的隔振频率存在一个30 Hz 左右的临界值。当隔振频率大于该临界值时，如果不增大扣件阻尼，减振垫很难取得减振效果。当隔振频率小于临界值时，减振垫与扣件的组合能取得较好的减振效果。当隔振频率大于临界值或无隔振措施时，仅减小扣件刚度并不一定能达到减振效果，甚至会放大振动。在选择减振扣件时，扣件阻尼需比普通扣件的阻尼大才有减振效果，而若扣件阻尼较小，则应选择垂向刚度较大的扣件。当隔振频率小于临界值时，配合不同的扣件可以取得较好的减振效果。也可根据插入损失，得到图12(a)中所示不同减振等级对应的扣件与减振垫的参数区域。

从图12(b)可知：在损耗因子为0.3 的情况下，Z 振级的最大值变化到20 kN/mm 的扣件与55 Hz隔振频率的减振垫匹配处。增大损耗因子，可使隧道壁有整体的减振作用。随损耗因子增大，隔振频率的临界值会降低，扣件与减振垫的综合减振效果(即插入损失)有所降低。换言之：若采用损耗因子较大的扣件，想取得同等级的减振效果，则需要选取更低隔振频率的减振垫或垂向刚度更大的扣件，或两者合理匹配使用。

为了量化研究隧道壁Z振级随扣件与减振垫的变化，图13所示为在扣件损耗因子为0.1 的情况下，减振垫与扣件刚度对隧道壁Z振级的影响，根据是否低于临界频率分为2类工况。

由图13(a)可知：在损耗因子为0.1 的情况下，减振垫的临界频率约为35 Hz，相比无隔振的情况，减振垫频率低于临界频率才能达到减振的效果。当隔振频率低于临界频率时，总体上是扣件刚度越大，减振效果越好。例如图13(a)中，量化地看，当扣件刚度从10 kN/m增加到60 kN/mm时，隧道壁Z 振级降低3.0～4.5 dB。当隔振频率小于临界频率时，减振垫的隔振频率越低，减振效果越好。例如图13(a)中，对比无隔振的情况，隔振频率为8 Hz的减振垫与扣件的组合能取得8～14 dB的减振效果。

由图13(b)可知：当隔振频率大于临界值时，减振垫与扣件的组合效果主要取决于扣件刚度。整体上看，隧道壁Z 振级在扣件刚度为20 kN/mm 时取得极大值，在扣件刚度为50 kN/mm时取得极小值。

图14所示为在扣件损耗因子为0.3 的情况下，减振垫与扣件刚度对隧道壁Z振级的影响。

由图14可知：当损耗因子增大时，临界频率会降低：损耗因子为0.3 的情况下临界频率为30 Hz。随损耗因子增大，至高于临界频率时，对比无隔振的情况，减振垫反倒会使Z振级增大。并且在隔振频率为50 Hz时取得极值。对比图13，损耗因子增大能整体降低隧道壁Z振级。

3.2.4 参数匹配对钢轨分频振级的影响

根据上述分析，为降低隧道壁Z振级，可选取隔振频率较低的减振垫与垂向刚度较大的扣件，而文献表明，较高级的减振措施往往会对轮轨关系、列车动力学性能(安全性、舒适性、平稳性及脱轨系数等)产生不利影响[20]。为探究减振措施对列车动力学性能的影响，在低频段，轮轨状态良好的情况下，轮轨是不分离的，因此钢轨振动与车轮振动是相对应的，与粗糙度和轮轨接触刚度等有关，即可以使用钢轨振动间接表征减振措施对列车动力学性能的影响[21]。图15和图16所示分别为扣件刚度和减振垫隔振频率对钢轨分频振级的影响规律。

由图15可知：

1)与隧道壁振级的规律相似，扣件刚度主要影响钢轨的振动级峰值频率分布，与轮轨耦合共振频率一致。

2)GB/T 5599—2019中指出车体动力学的分析频率为40 Hz以下，在该分析频率范围内，降低扣件刚度会增大钢轨振动，进而增大列车的振动，从而降低列车运行的动力学性能。

由图16可知：随隔振频率降低，钢轨的振动级整体地增大，在8～80 Hz 的频率范围内尤其明显。在40 Hz的分析频率范围内，降低减振垫隔振频率会增大钢轨振动，进而增大列车的振动，从而降低列车运行的动力学性能。因此，在降低环境振动的同时，也需要注意轨道结构以及列车的稳定和舒适性等问题。降低减振垫隔振频率对100 Hz 以上的钢轨振动影响较小，因此，对轮轨噪声也不会产生较大影响。

4 结论

1)隧道壁的振动级随频率增加整体呈增大趋势，在25～80 Hz 频率范围内，存在局部最大值，该局部峰值频率与轮轨耦合共振频率一致。

2)隧道壁Z 振级在参数匹配过程中，存在最大值与最小值，最小值出现在60 kN/mm的扣件与8 Hz 隔振频率的减振垫组合处，最大值与扣件阻尼有关。

3)减振垫的隔振频率存在一个30 Hz附近的临界值。当隔振频率大于该临界值时，对隧道壁的减振效果有限，甚至会放大振动。当隔振频率小于临界值时，减振垫与扣件的组合能取得较好的减振效果。扣件刚度、阻尼应与减振垫隔振频率匹配使用，以取得最优匹配效果。

4)当隔振频率小于临界频率时，扣件刚度越大，减振效果越好，即当采用隔振频率小于30 Hz的减振垫或橡胶浮置板时，应尽可能选择刚度较大的扣件。对于无隔振的情况，在扣件刚度取50 kN/mm时，隧道壁Z振级取得极小值。

5)减振垫的隔振频率越小，对隧道壁的减振效果越好，但同时也会使列车动力学性能变差，而对轮轨噪声的影响不大。因此，在使用减振措施降低列车运行引起的环境振动时，也需要兼顾减振措施对列车的动力学性能的影响。

6)本文验证了模型的正确性，并针对隧道壁振动研究了轨道结构的最优匹配设计。在此基础上，下一步将针对地表振动、上部建筑物的振动开展研究，考虑土层的影响与房屋耦合振动，研究减振轨道结构的最优匹配设计。