高温季节轨道板温度模型的热流时延效应分析

方若望，何越磊，李再帏，路宏遥，赵彦旭

（1. 上海工程技术大学城市轨道交通学院，上海 201620；2. 中铁二十一局集团有限公司，甘肃 兰州 730070）

CRTSⅡ型板式无砟轨道作为我国高速铁路重要组成结构，其混凝土结构破坏与温度效应有重要关系[1]。 温度作用力的剧烈变化会使轨道板产生诸多病害，常见的有裂缝、挤压掉块和翘曲变形[2-3]。 轨道结构在长期的温度荷载变化下会产生不可逆转的损伤，其中由于纵向的伸缩变形将导致宽窄接缝区域破损掉块[4]，轨道结构整体升温对轨道板与砂浆层界面开裂影响较大[5]，竖向温度梯度是引起砂浆层界面离缝的主要原因。 诸多研究探讨了温度梯度对无砟轨道的结构特性影响。 钟垚等[6]研究高温条件及最高设计正温度梯度下，轨道板与砂浆层之间仍会产生层间离缝且靠近板角位置更为严重。Song 等[7]提出了CRTSⅡ板式无砟轨道结构热变形和界面分离的分析方法， 揭示了CRTSⅡ板式无砟轨道结构在自然环境条件下的温度场、 热变形、界面损伤和界面分离的特点。 刘钰等[8]指出考虑热效应引起的应力是正确设计结构的必要环节，提出了一种基于有限元方法的混凝土结构在时、空变温度荷载作用下应力应变分析的数值方法。 现有的大部分研究[9-10]默认热传播速度无限大，系统时刻处于平衡状态。 但在实际问题中，从状态发生改变到建立平衡存在时间差，即由于温度差异导致的热传递具有延迟效应。本文以华东某线路CRTSⅡ型板式无砟轨道为例，研究环境温度、太阳辐射等外界因素与轨道板自身内因对轨道板内部温度分布的影响。 建立基于热流时延的轨道板系统温度模型，为后续在不破坏轨道结构的前提下评估轨道结构受力变形和维护提供理论依据。 包括指导施工作业，防止因破坏轨道结构产生巨大的温度梯度及应力。

1 无砟轨道板内温度分析

白天，轨道板表面由于外界环境因素升温，并通过分子热传导向深处传递热量；夜间，轨道板表面因与自然环境热交换而首先冷却， 热量从板深处向上输送。 轨道板温度的变化首先从表面开始，逐渐影响深层板温度的变化， 其变化幅度随深度的增加而减少。 轨道板中热量传递的大小与快慢还与板自身特性有关。 在自然科学土壤研究中[11]，若土壤是均质的， 其深处的传热仅通过分子的热传导， 而且土壤表面温度随时间有周期性变化，则土壤内温度的变化遵循傅里叶定律：热量转递愈深，则温度周期变化的振幅衰减的越多；由温度梯度引起的热流之间的延迟时间与传播距离成正比。

上述理念用公式展现，将其应用到轨道板温度变化中，假设轨道板中混凝土是均质的，初步得到轨道板板内温度简易关系，即轨道板内部温度由表层温度曲线经过幅值变化和平移所得，结果如下

式中：T 为某一深度轨道板的温度，K；τ 为轨道板不同深度温度变化与轨道板表层的时间差，h；d 为深度，m； γ 为不同深度温度幅值与轨道板表层的比值；T表为轨道板表层温度，K；为表层平均温度，K；为不同深度的平均温度，K。

2 热力学板温求解模型

式（1）可大致反映出轨道板内温度与板表的对应关系。 但是作为轨道板结构与外界环境的交界部位， 轨道板表层温度受外界环境因素变化更为敏感，且存在突变的情形。 为了减少由于仪器自身原因或者记录到的环境因素偶发变化带来的影响，本文进一步考虑热力学因素加入修正项来减少误差。

2.1 太阳辐射

对监测的太阳辐射数据进行如下处理：先通过3 次样条插值运算丰富数据量， 然后采用复化Simpson 公式对时间段求积分。 对前2 h 吸收的太阳辐射求均值， 作为该时间段影响轨道板温度变化的太阳辐射量。 将区间 ［a，b］ 分成n 个子区间[xj，xj＋1]（j=0，1，…，n-1），第j 个子区间的中点为xj＋0.5，子区间长度为h。

应用复化Simpson 公式的太阳辐射求解公式如下

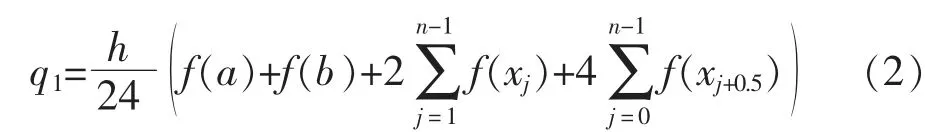
式中：f（a）为2 h 前的时刻测得的太阳辐射值，W/m2；f（b）为该时刻测得的太阳辐射值，W/m2。

2.2 热对流

热对流指的是在温差的作用下，由流体的运动所引起的热量传递。 通常为了方便起见，工程上采用牛顿冷却定律[12]来计算混凝土表面与空气的对流换热密度，计算式为

式中：hc为对流传热系数，W/（m2·K），它取决于流体和固体表面的固有特性以及流体的速度分布，固体的温度分布；Ts，Tu分别为轨道板表面温度和空气温度，K。本文计算混凝土结构表面的对流换热系数采用Saetta 等[13]给出的对流换热公式，计算式为

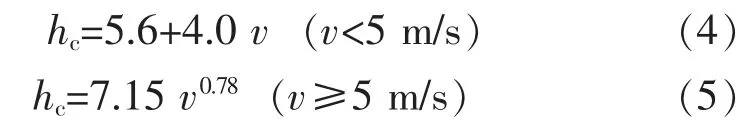
式中：v 为风速，m/s。

2.3 热辐射

任何具有温度的物体，其热能将通过电磁波的形式向外发射能量，这种现象称之为热辐射。 本文采用式（6）对轨道板混凝土表面热辐射能量密度进行计算

式中：ε 为表面黑度， 对于混凝土可取0.94；σ 是黑体辐射常数，为5.67×10-8W/(m2·K4)。

2.4 热流板温模型

轨道板表层净吸收的热流密度如下

式中：q 为净热流密度，表示单位时间单位面积通过的热量，W/m2；q1是太阳辐射密度，W/m2；q2是热对流密度，W/m2；q3是热辐射密度，W/m2。

以轨道板表层吸收的净能量所能转化的温度量减去实际轨道板表层温度的变化量，剩余部分作为修正项来减小误差。

将轨道板温度场计算假设为一维热传导问题，则轨道板内部温度可大致看成是轨道板表层温度曲线经过幅值放缩，相位延后所得。 由式（1）结合热传递理论下的修正项，可得出轨道板板内不同深度温度计算公式如下

式中：β 为能量转化为温度的转化系数， 取0.004；ΔT表为表层温度实测变化值，K。

以式（8）为核心计算公式，构成最终轨道板内不同深度温度计算模型。区别于温度拟合预测[14]，考虑了实时环境因素对轨道板内温度带来的影响，更有理论依据。 对于不同地区的轨道板内温度变化规律，其幅值衰减γ 与延迟时间τ 有所不同。

3 热流时延模型计算

以华东地区某高速铁路2018 年7 月26 日到8月25 日期间测得的数据作为试验计算验证依据，数据内容包括风速、太阳辐射、环境温度、轨道板表层及不同深度温度等，数据收集间隔为0.5 h。 监测的板温数据为路基轨道板板中位置， 具体位置如图1 所示。

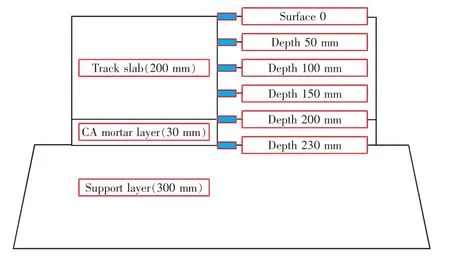
图1 轨道板温度监测位置示意图Fig.1 Schematic diagram of track plate temperature monitoring position

3.1 实测轨道板温度曲线

实测轨道板温度曲线验证了热流存在时延，并且幅值衰减的理论（图2）。

图2 轨道板内不同深度温度曲线Fig.2 Temperature curves of different depths in track slab

3.2 轨道板不同深度温度频域曲线

为了得出轨道板表层与不同深度温度曲线关系的参数，采用频谱分析的方法[15]，求出相应的τ，γ与深度d 的关系。 将测得的温度数据傅里叶变换后，得到如图3（a）所示频域特性。 轨道板表层与不同深度温度频域特性相似，仅在频率为1.158×10-5Hz时，温度峰值有较大区别，对应的周期为23.99 h。其余频率峰值相较于前者可忽略不计，本文仅考虑最大处峰值所蕴含的信息。若记表层温度峰值为1，得到各深度峰值的拟合函数为

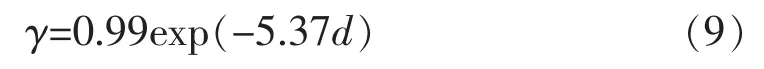
式中：γ 为轨道板各深度处温度峰值相对表层的比值；d 为深度，m。 由式（9）可得出轨道板内各处温度幅值随深度呈指数衰减。

若记表层温度峰值初始相位为0， 得到各深度温度相位的拟合函数为

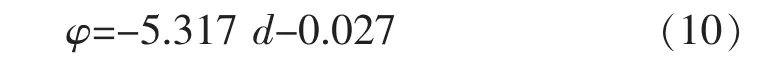
式中：φ 为轨道板各深度处温度相对表层的滞后相位。 由式（10）可得出轨道板内各处温度相位随深度呈线性滞后。由图3（c）相位差推时间差，得

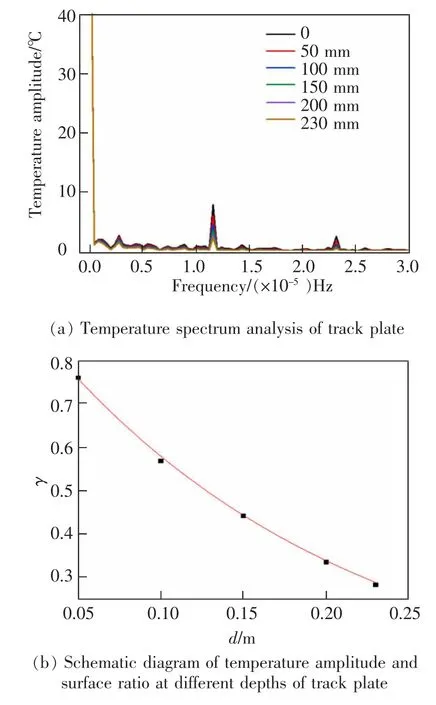
图3 轨道板不同深度温度频域特征Fig.3 Frequency domain characteristics of temperature at different depths of track slab

式中：τ 为轨道板不同深度温度变化相较于轨道板表面的时间差，h，负号代表延迟。

表1 不同深度温度变化时间延迟Tab.1 Time delay of temperature change at different depths

上述频域分析表明，轨道板不同深度温度相对表层温度序列，振幅以指数函数衰减，相位存在线性滞后。 同时也证明了无砟轨道板板内温度热流时延模型的可靠性。

4 热流时延模型验证

由本文热流时延模型计算所得的不同深度温度曲线与实测温度对照展示如图4。 由图4 可以看出，最终求得的不同深度温度曲线与实测温度曲线吻合得较好，进而求出其平均相对误差并进行可靠度分析（表2）。

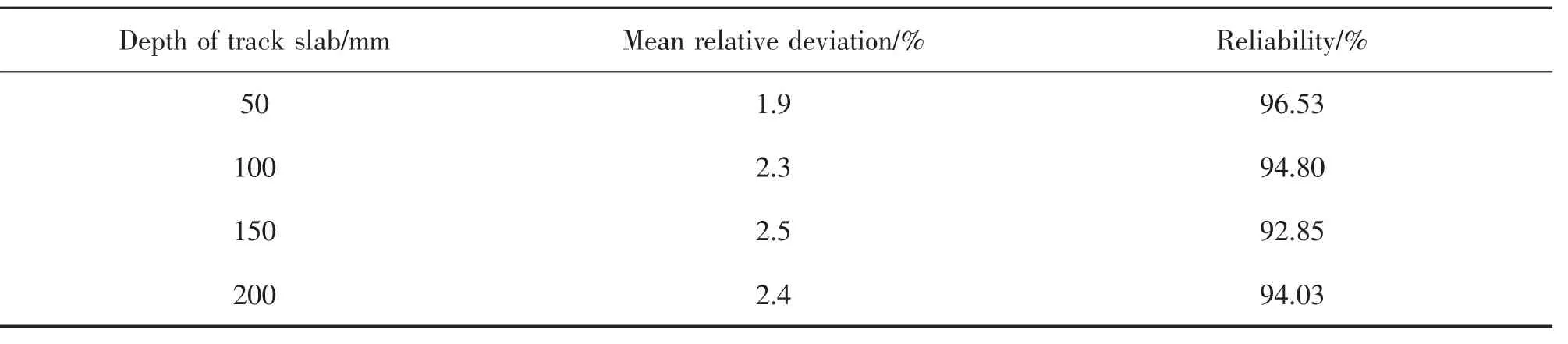
表2 计算所得温度的平均相对误差与可靠度Tab.2 Average relative error and reliability of calculated temperature

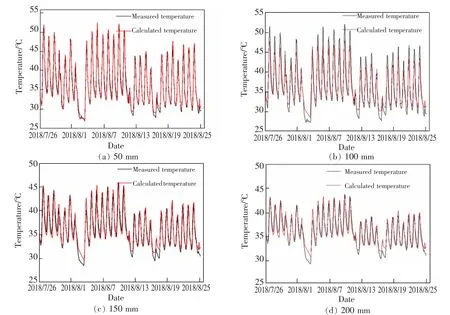
图4 轨道板不同深度计算温度对照Fig.4 Comparison of calculated temperature at different depths of track slab

计算求得的轨道板各深度温度相对于实际温度数据的平均相对误差在1.9%～2.5%。 统计绝对误差大于2 ℃的点占总监测点数的比例为D。 定义可靠度为1-D，结果显示在92.85%～96.53%，满足实验要求。

5 结论

本文考虑输入状态发生改变到建立平衡存在时间差，把时间延迟引入到轨道板混凝土热力学分析。 从温度场作用于轨道板混凝土结构将改变其性能的点出发，分析了热力学中不同的温度传递方式以及热流密度对轨道板内温度变化的影响。 得出以下结论。

1） 对轨道板温度进行频谱分析得出轨道板内各处温度幅值随深度呈指数衰减， 温度相位随深度呈线性滞后。 热量在轨道板中传递时， 每深入50 mm，轨道板温度变化延迟时间约1.02 h。

2） 轨道板表面吸收的净热量除去部分转化为内能，剩余量作为修正项避免了由于仪器自身原因或者记录到的环境瞬态变化带来的影响。 与对温度拟合预测相比，考虑了实时环境因素对轨道板内温度带来的影响，更有理论依据。

3） 考虑了热力学理论的温度计算模型平均相对误差在1.9%～2.5%， 可靠度在92.85%～96.53%，为后续在不破坏轨道结构的前提下分析轨道板应力及维护提供参考。

4） 为简化模型，未考虑长期阴雨天温度的复杂变化，期间会有较大误差。