基于HJC 模型的车辆-桥墩碰撞响应分析

任 亮，万 超，喻贤明

（1. 华东交通大学土木建筑学院，江西 南昌 330013; 2. 华东交通大学土木工程国家实验教学示范中心，江西 南昌 330013）

近年来，随着我国经济的高速发展，对交通的需求日益增大，道路立交桥等跨线结构物的大量修建成为缓解城市地面交通压力的重要途径。 但受车辆超载超限、路政管理不健全、驾驶失误等因素的影响，车辆撞击桥梁事故屡屡发生，造成巨大的经济损失和社会影响。

为适应桥梁结构抗撞击的需求，已有学者通过实车撞击试验和缩尺撞击试验对车辆-桥墩碰撞过程开展了受力机理和变形性能等方面的研究[1]。 但考虑到试验费用昂贵、试验过程复杂及撞击影响参数过多，大多数学者通过数值分析[2-3]对车辆撞击桥墩事故进行重现，以获得桥墩在车辆碰撞作用下的损伤劣化过程， 其中大型有限元程序LS-DYNA 因其为用户提供了许多能够反映材料力学性能的损伤模型如CSC 模型、HJC 模型等[4-5]，而被广泛应用于车辆-桥墩碰撞有限元数值模拟中。 依托CSC 模型，通过建立车辆-桥墩碰撞有限元模型，国内外学者相继探讨了车重和车速对车辆-桥墩碰撞受力性能和破坏模式的影响[6-7]，评估了不同边界条件和箍筋直径的桥墩在车辆撞击作用下的动力响应及损伤特征[8-9]，分析了车辆类型对桥墩撞击力和位移的影响[10-11]。而对于HJC 模型，虽然也有学者应用其开展了车桥碰撞数值研究[12]，但对模型的有效性并未进行相关验证， 其适用性和可靠性仍有待深入研究。

针对上述问题， 为探讨HJC 模型在车辆-桥墩碰撞数值分析中的适用性，本文应用大型有限元程序LS-DYNA， 首先明确HJC 模型中关键参数的取值， 建立落锤冲击试验数值模型并开展试验验证；在此基础上进一步构建车辆-桥墩碰撞有限元模型，探讨车重、车速和撞击位置对钢筋混凝土桥墩撞击力与墩顶位移的影响。

1 HJC 模型

HJC 模型是一种与应变率相关的损伤模型，它通过确定损伤函数和静水压力-体积应变关系来建立屈服面方程[13]，如图1 所示（图中σ*为等效应力σ 与单轴抗压强度fc′的比值；P*为静水压力P 与单轴抗压强度fc′的比值；T*为最大拉伸强度；D 为取值范围在0 与1 之间的损伤参数；ε*为真实应变率）。 其中屈服面方程控制参数包括：归一化内聚强度系数A，归一化压力系数B，应变硬化指数N，应变率系数C 和最大归一化强度SMAX；损伤函数控制参数包括： 损伤参数D1和D2以及破坏时最小塑性应变EFMIN；静水压力-体积应变方程控制参数包括：弹性极限静水压力Pcrush，弹性极限体积应变μcrush，压实静水压力Plock和压实体积应变μlock。

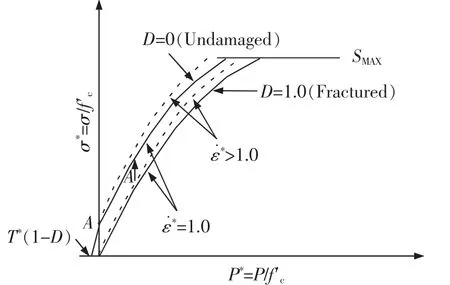
图1 屈服面方程Fig.1 Equation of yield surface

上述参数中A、B、N、SMAX、C、D2、EFMIN取值与混凝土强度无关，一般参考Homquist[14]推荐的普通混凝土初始取值，D1根据混凝土最大拉伸强度计算求得[15]，Pcrush、 μcrush、Plock、 μlock则基于混凝土单轴抗压强度进行取值[16]。

以C30 混凝土为例， 应用上述参数确定方法，得到HJC 模型中关键参数取值如表1 所示。

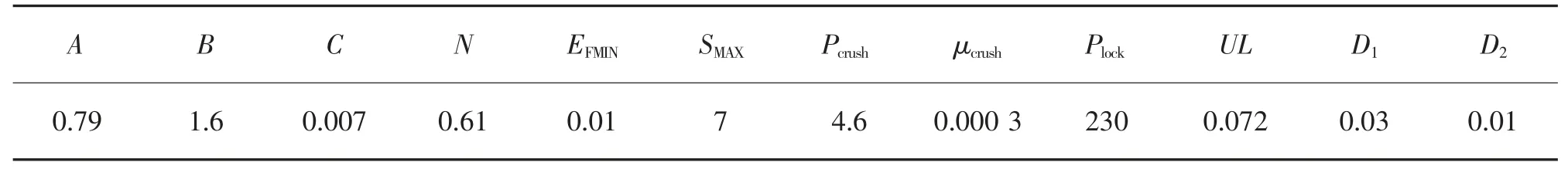
表1 HJC 模型参数（C30 混凝土）Tab.1 Parameters of HJC model （C30 concrete）

2 基于落锤试验的HJC 模型验证

2.1 落锤冲击试验有限元模型

受试验条件限制， 很难开展实车-桥墩碰撞试验评估上述HJC 模型参数取值的适用性。 为此，本文选用文献[17]中开展的落锤冲击试验，通过建立基于HJC 模型的有限元模型， 结合试验数据，对HJC 模型参数取值的可靠性进行验证，图2 为相应的试验装置。

图2 落锤试验装置（单位：mm）Fig.2 Drop-weight test device（Unit：mm）

在图2 中钢筋混凝土梁长4 000 mm，截面尺寸为300 mm×300 mm，材料为C30 混凝土，相应的单轴抗压强度为34.9 MPa。 试件纵筋采用4 根直径为25 mm 的HRB400 钢筋， 箍筋采用直径为12 mm、间距150 mm 的HRB400 钢筋， 混凝土保护层厚度为35 mm。

依据试验参数建立的落锤冲击有限元模型如图3 所示。 其中钢筋采用梁单元模拟，通过随动硬化模型考虑其损伤行为； 混凝土采用实体单元模拟，通过HJC 模型考虑其损伤劣化行为；落锤采用实体单元进行模拟，落锤与钢筋混凝土梁之间设置为面面接触，梁两端分别以滑动支座和固定支座进行约束。

图3 落锤冲击有限元模型Fig.3 Finite element model of drop-weight test

2.2 试验结果与数值结果对比

图4 给出了文献[17]中试件在落锤作用下跨中位移和冲击力时程曲线与计算曲线对比。 从图中可以看出计算的位移时程曲线和冲击力时程曲线与实测曲线大致吻合。 其中计算的跨中位移峰值为31.37 mm，试验值为30.9 mm，两者偏差仅为1.52%；计算的冲击力峰值为586 kN，试验值为572 kN，两者偏差仅为2.45%，表明本文选取的HJC 模型关键参数具有较好的适用性。

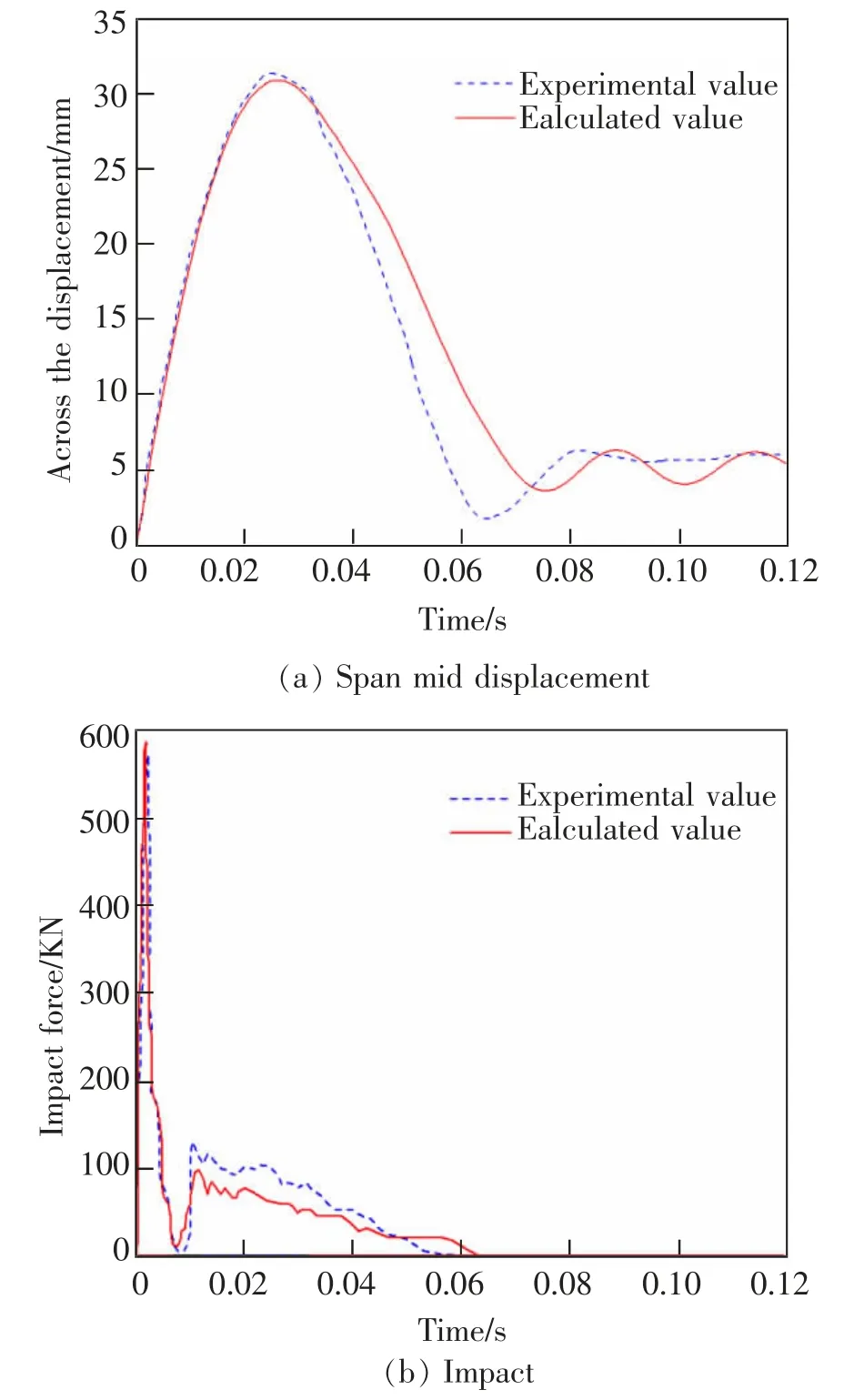
图4 落锤冲击响应计算曲线与试验曲线对比Fig.4 Comparison between calculation curve and test curve of impact response of drop-weight test

3 车辆-桥墩碰撞有限元模型

3.1 车辆模型

车辆模型选用美国国家碰撞中心（National Crash Analysis Center, NCAC）[18]公布的Ford800 车辆有限元模型（如图5 所示）。 该车为两轴卡车，车轮轴距5.29 m，车宽2.44 m，车身总长8.54 m，总质量为8 t，其中压载货物为2.9 t。 整车模型主要由6个部件构成，其中车轮、发动机和货物皆采用实体单元进行模拟，车架采用梁单元进行模拟，车头和底盘建模则采用壳单元进行模拟，车辆重量可通过调整货物重量来进行控制。

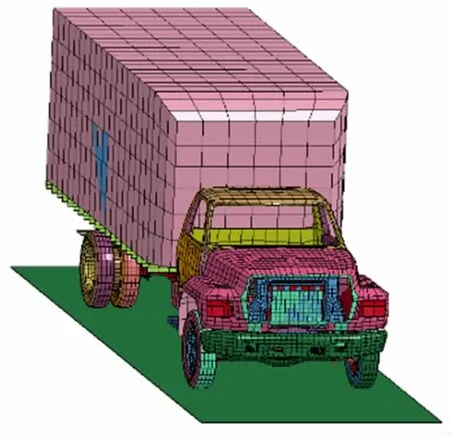
图5 Ford800 有限元模型Fig.5 Finite element model of Ford800

3.2 桥墩模型

桥墩选用城市桥梁中常用的直径为0.8 m、混凝土强度为C30 的钢筋混凝土桥墩，其中纵筋和箍筋直径分别为13 mm 和11 mm，均采用HRB400 钢筋。 分析时墩身和钢筋分别采用实体单元和梁单元进行模拟，以上述验证后的HJC 模型模拟混凝土材料的损伤行为，以随动硬化模型模拟纵筋和箍筋的受力性能， 如图6 所示。 考虑桩-土相互作用对车辆-桥墩撞击影响不大[19]，边界处理时选用固定约束对桥墩底部边界进行简化； 车辆-桥墩之间采用面面接触， 不考虑钢筋与混凝土之间的相对滑动；通过在墩顶添加一个向下的轴向均布荷载来模拟上部结构对桥墩的荷载作用[20]。

图6 钢筋混凝土桥墩模型Fig.6 Model of reinforced concrete pier

4 车辆-桥墩碰撞有限元模型验证

可靠的车辆-桥墩碰撞有限元模型能合理反映出碰撞过程中的系统能量转换[21]，可通过对计算过程产生的沙漏能和滑移能进行严格监控来验证车辆-桥墩碰撞有限元模型的有效性。 当碰撞过程中的沙漏能以及滑移能占比小于总能量的10%时，则说明碰撞过程中能量损失控制良好，数值模拟较为可靠。 图7 为质量8 t 的卡车以80 km/h 的速度撞击桥墩时的能量转换时程曲线。

图7 能量转换-时程曲线Fig.7 Energy conversion-time history curve

从图7 中可以看出，车辆-桥墩碰撞初始阶段，系统的总能量仅为车辆动能。 随着碰撞的持续进行，系统动能逐渐减小，内能、沙漏能和滑移能逐渐增加，总能量有轻微浮动但基本保持不变。 当碰撞趋于平稳时，各项能量变化接近水平，取能量曲线的水平值作为最终能量值，计算的沙漏能和滑移能占比如下：

从上述计算结果可以看出：平稳后的总能量为1.97 MJ， 沙漏能、 滑移能各占总能量的1.27%和1.52%，皆小于总能量的10%，表明建立的车辆-桥墩碰撞计算模型具有较好的精准性。

5 参数分析

为进一步探讨车辆-桥墩碰撞参数改变对撞击性能产生的影响，对不同撞击速度、撞击质量和撞击位置下的桥墩撞击响应进行分析。 其中车辆原型为前述的Ford800，基本车重为8 t，当开展不同撞击速度和撞击质量分析时， 车辆-桥墩碰撞位置为偏心距为零的正面碰撞。

5.1 撞击速度

图8 和图9 分别为质量8 t 的卡车在不同撞击速度下的撞击力时程曲线和墩顶位移时程曲线对比。

从图8 中可以看出，撞击力峰值随撞击速度的增大呈线性递增且撞击力峰值发生时间逐渐提前，这是由于撞击速度的提升有效增大了撞击能量，从而增大了撞击力峰值并加速了发生时间。 当时速大于100 km/h，撞击力时程曲线明显出现了两个峰值，这是由于高速撞击时车厢将产生二次碰撞所致。

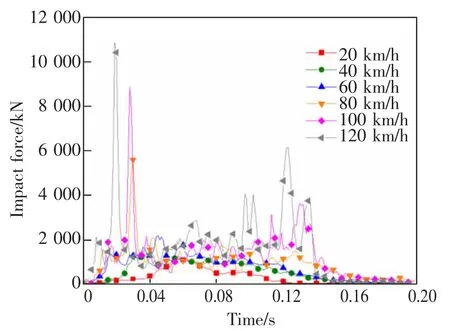
图8 不同撞击速度下撞击力-时程曲线

从图9 中可以看出，在不同撞击速度下，墩顶位移时程曲线均存在两个碰撞峰值，且两个位移峰值均随撞击速度的增加而逐渐增大，当撞击速度超过100 km/h 时，第2 个墩顶位移碰撞峰值急剧增大并超过第1 个墩顶位移峰值，这是由于第2 次车厢撞击效应叠加在第1 次车头撞击效应之上所致，表明车辆-桥墩碰撞达到一定的撞击能量后应考虑二次碰撞效应的影响。

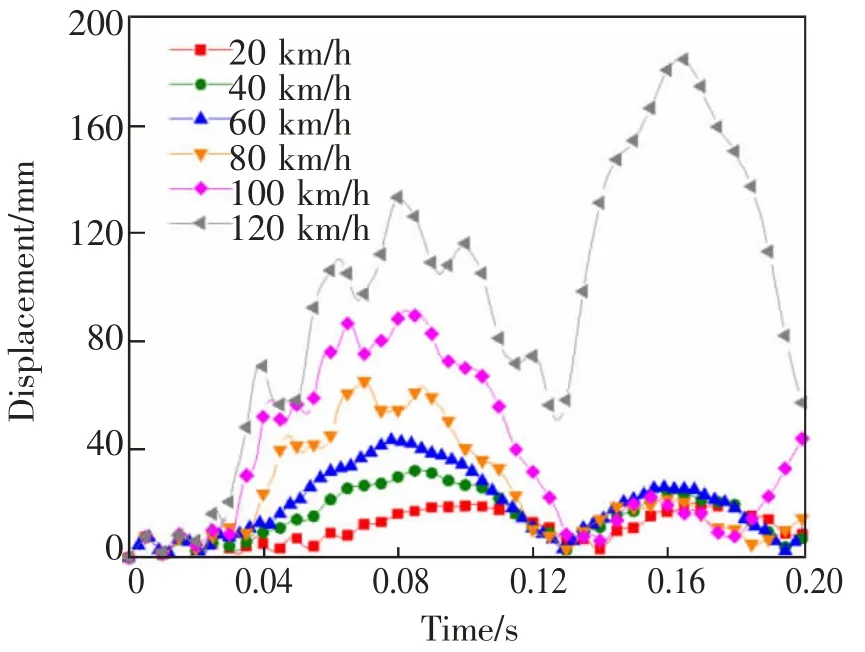
图9 不同撞击速度下墩顶位移-时程曲线Fig.9 Displacement-time history curves under different impact velocities at the pier top

5.2 撞击质量

图10 和图11 分别为撞击速度80 km/h 的卡车在不同撞击质量下的撞击力时程曲线和墩顶位移时程曲线对比。

从图10 和图11 中可以看出， 撞击力和墩顶位移峰值随着撞击质量的增大呈线性递增，但撞击力峰值发生的时间逐渐后移，这是由于撞击质量的增大会加剧车辆-桥墩碰撞碰撞后的变形形态，从而提高撞击力峰值；与此同时，车辆的形变在一定程度对碰撞过程起到类似阻尼效应，进而在一定程度上延缓了撞击力峰值和墩顶位移峰值的出现。

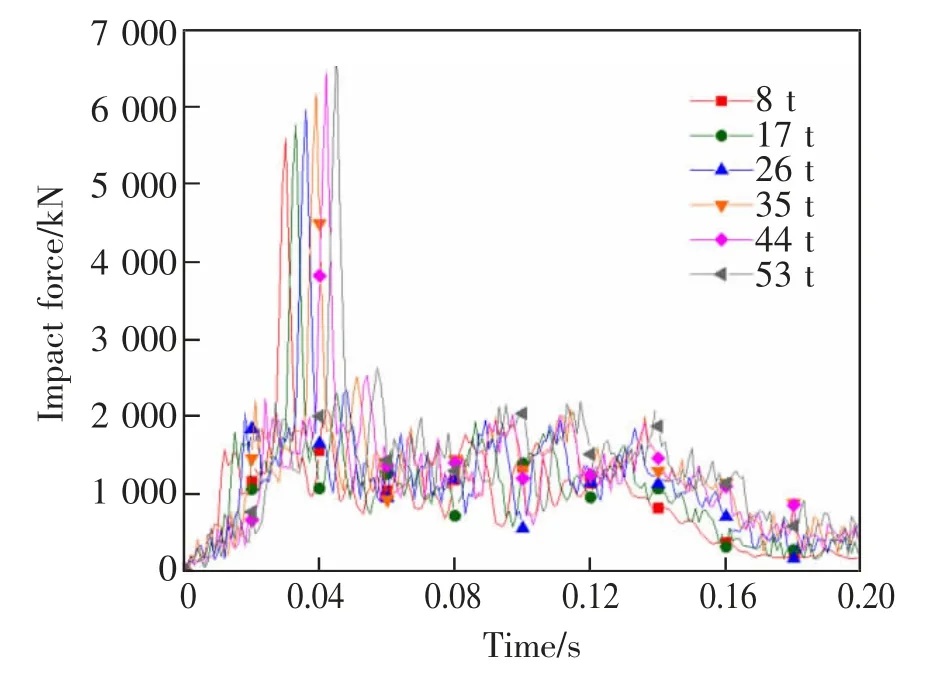
图10 不同撞击质量下撞击力-时程曲线Fig.10 Impact force time history curves under different impact masses

图11 不同撞击质量下墩顶位移-时程曲线Fig.11 Displacement-time history curves under different impact masses at the pier top

5.3 撞击位置

图12 和图13 分别为撞击速度80 km/h、 撞击质量8 t 的卡车在不同撞击位置时桥墩的撞击力时程曲线和墩顶位移时程曲线对比，其中撞击位置由车辆-桥墩撞击偏心距衡量， 相应的偏心距为车辆与桥墩中心轴偏离的距离， 偏心距为0 表示车辆-桥墩正面相撞。

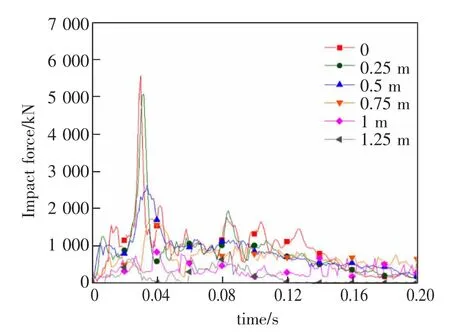
图12 不同撞击位置下撞击力-时程曲线Fig.12 Impact force-time history curves under different impact positions

图13 不同撞击位置下墩顶位移-时程曲线Fig.13 Displacement-time history curves under different impact positions at the pier top

从图12 和图13 中可以看出，在相同的撞击速度和撞击质量下，撞击力和墩顶位移峰值会随着撞击偏心距的增大而逐渐减小， 车辆-桥墩正面相撞时撞击力和墩顶位移峰值最大。 这是由于撞击偏心距的增大会影响撞击荷载的作用位置并减少撞击过程中车辆和桥墩的接触面积， 从而对车辆-桥墩的撞击效应起到一定的削弱作用所致。

6 结论

本文应用大型有限元程序LS-DYNA， 明确了HJC 模型中关键参数取值，建立了落锤冲击试验数值模型并开展试验验证；在此基础上进一步构建了车辆-桥墩碰撞有限元模型，探讨了车重、车速和撞击位置对钢筋混凝土桥墩撞击力与墩顶位移的影响，得出结论如下：

1）综合考虑落锤试验和数值模型的差异性，结合合适的参数选取，应用HJC 模型能较好的模拟落锤冲击作用下的冲击力-时程曲线和跨中位移-时程曲线。

2）基于HJC 模型建立的车辆-桥墩碰撞分析模型在碰撞过程中总能量基本保持不变，沙漏能和滑移能占比仅为1.27%和1.52%，具有较好的精准性。

3） 撞击力和墩顶位移峰值随撞击速度和撞击质量的增加而增大，但撞击速度的提升将加快峰值响应的出现，而撞击质量的增大将延缓峰值响应的出现。 当车速超过100 km/h 时，撞击力和墩顶位移时程曲线将出现两个显著的峰值，应考虑车厢的二次撞击响应。

4）车辆-桥墩碰撞效应随撞击偏心距的增大逐渐削弱， 车辆-桥墩正面相撞时撞击力峰值和墩顶位移峰值最大。