复合地层微型盾构机刀盘受力性状及布置优化

蒲亚平

（中铁十八局集团第一工程有限公司，河北 涿州 072750）

行业内通常把直径小于3 m 的盾构机称为微型盾构机[1]。 近年来，微型盾构已广泛应用于广东、福建等滨海省份城市的给排水隧道、 电力隧道、综合管廊等市政工程领域中[2]，在城市建设中发挥着越来越重要的作用[3]。 而刀盘作为盾构机的关键部件[4]，刀盘的结构类型、刀具的数目及其布置会对刀具的使用寿命产生直接影响，进而影响整个盾构工程的安全性、经济性和效率[5]。 为了确保微型盾构机在滨海复合地层条件下的正常掘进，对微型盾构机的刀盘设计和刀具的布置方法进行研究具有重要的工程意义。

目前国内外众多学者对盾构机刀盘的设计进行了大量的研究。 Dahl 等[6]通过对Sievers 的J 微型钻探测试方法的改进， 得到了直接估计刀具寿命的新方法，为刀具布局奠定了基础。 蒲毅等[7]结合阿基米德螺旋线布刀法以及刀具磨损等寿命布刀原则，提出切刀应该对称布置以适应刀盘正、反转的实际使用需求， 为土压平衡式盾构机刀盘面板上的刀具布置奠定了理论基础。 学者利用改良的渣土具有“塑性流变状态”的特性，采用CFD 流体软件实现了刀盘结构动态切削仿真模型， 并通过研究刀盘的开口分布特性得到刀盘拓扑优化结构[8-9]。 Nilsen[10]通过有限元软件采用静力学板块进行盾构刀盘结构强度验算， 考虑在土体材料非线性的基础上进行了刀盘动态仿真以及优化分析。田继涛等[11]等人经过研究确定盾构刀盘的牛腿和法兰盘的牛腿边缘部位最为薄弱， 采用多目标遗传算法优化了刀盘的几何参数以及开口率， 为盾构刀盘结构优化提供了一定思路。 韩伟峰等[12]通过有限元软件对盾构刀盘进行强度验算以及模态分析， 采用蒙特卡罗抽样技术对刀盘的设计缺陷之处进行优化设计， 从而提高了刀盘整体使用性能，而且还能够达到减重降本的效果。 他们的研究主要针对实际施工中大型盾构机的刀盘、 刀具布置及仿真优化， 尚未对微型盾构机刀盘的结构参数进行系统性的优化设计。 而且，国内厂家在生产微型刀盘过程中往往是将大中型刀盘等比例缩小，这样设计出的刀盘其选择的刀具类型、数量及布置方法并不合理，并缺乏对地质状况的分析，不利于整个盾构工程的安全性、 经济性和工作效率[1]。如何解决微型盾构机的刀具布置单按比例缩小大型盾构机的刀盘结构这一问题成了微型盾构刀盘结构设计的一项关键技术。

除此之外， 微型盾构机在穿越滨海地层时盾构机刀盘与地层相适应性的研究尚未探明， 学者在利用盾构模型机探究盾构刀盘与地层相适应性时， 往往是量身定做并且只适用研究在单一的卵石、砂土、软土、黏土层掘进过程中存在的问题[13-19]，对于软硬不均、全～微风化花岗岩等滨海复杂地层需要多种模式的微型盾构机则显得难以适用，并且盾构模型机对于刀盘、 刀具也只是简单进行设计、布置，采用模型试验得到的数据与理论值精度存在一定的差距。

本文以滨海复合地层为工程背景， 基于双滚刀协同破岩原理确定最优滚刀间距， 对比分析3种整体式切刀布刀法的优劣， 通过动态仿真有限元模型确定最优刀盘结构， 并核验了不同工况下的刀盘结构受力性状， 有效解决微型盾构机的刀具布置单按比例缩小大型盾构机的刀盘结构这一问题，可实现小直径盾构机对土体的全面切削，对滨海复杂地层中微型盾构机刀盘优化设计具有参考意义。

1 刀盘结构选型

刀盘作为机械化盾构的掘削机构，在盾构掘进过程中不仅承担着开挖土体的作用，同时刀盘面板还可稳定掌子面，并且刀盘旋转过程中会对渣土进行搅拌，改良渣土的塑性状态，有利于排渣运土。 市场上刀盘结构的主流型式有3 种，即面板式、辐条式以及辐板式。 其中，辐板式刀盘不仅兼有面板式和辐条式的优点，整个刀盘面板上不仅可以看到较宽的辐条结构， 而且还能看到小块的面板结构，其开口率通常为35%～50%[18]，切削类刀具对称布置在辐条的两侧， 而滚刀直接安装在辐条内部的刀座上，主要适用于复合地层。

滨海复杂地质条件可按复合地层来考虑，刀盘结构采用辐板式，开口率的取值范围为25%～45%。为确定小直径盾构机刀盘最佳结构型式，针对常用的三辐条三面板和四辐条四面板辐板式结构，分别建立四辐条四面板和三辐条三面板式刀盘结构的三维模型。刀盘直径取600 mm，厚度选取40 mm，开口率40%， 整体刀盘结构不考虑刀具的精细化布置，可通过一定的刀刃代替切削刀具，并对刀盘施加一定的推力以及扭矩，通过分析刀盘结构的应力应变来进行优选。刀盘结构材料选择Q345 钢，采用四面体模型。 最终，依据静力分析结果，四辐条四面板式刀盘结构的最大应力为21.92 MPa， 三辐条三面板式刀盘结构的最大应力达到了30.84 MPa，且四辐条式的刀盘面板比三辐条式的刀盘面板受力更均匀；因此，选用四辐条四面板式刀盘结构作为掘削刀盘。 同时，滨海地层岩性复杂，为了后续适应不同地层的掘进试验，刀盘开口率进行了可变式设计，通过对辐板进行可拆卸式设计，从而达到调整开口率的目的。

2 刀盘布置设计有限元模拟

2.1 双滚刀作用下协同破岩过程模拟

合适的刀间距可使滚刀在破岩过程中各自产生的裂纹相交从而加大岩石破碎量，提高滚刀破岩效率， 通过进行不同刀间距的双滚刀破岩数值仿真，可为滚刀在盾构模型机的刀盘面板上进行布置时找到最优刀间距[19]。

岩石材料选取滨海地层的花岗岩，刀具选用已进行参数优选的滚刀刀圈， 分别建立圆心为参考点并与滚刀刀圈耦合成刚体约束， 滚压速度为20 mm/s，滚刀转速1 rad/s，切入深度2 mm，两刀圈都同时以相同滚压速度以及转速进行破岩仿真，同时对模型底部采用全约束， 两侧采用进行对称约束约束，以减少反射波的影响，并对中心区域的岩石单元进行网格加密，提高计算精度。

根据剪切破坏理论，岩石在滚刀破岩过程中形成破裂宽度a=P/tanα，如图1 所示。其中在刀盘面板上相邻滚刀的刀刃贯入度是一样的，在刀盘面板上布置滚刀时， 相邻滚刀之间的刀间距不能太大，以免形成岩脊未能完全切割整个开挖面，滚刀之间的刀间距应满足

图1 盘形滚刀破岩过程示意图Fig.1 Schematic diagram of rock breaking process with disc cutters

式中：S 为刀间距；P 为贯入度；α 为岩石的压裂角，通常为18°～30°，这里取29°；a 为岩石破裂宽度；b 为滚刀刀圈宽度，与刀圈直径、结构有关，这里取5 mm。

代入相关数据，计算可得刀间距。 为了确定最优刀间距， 分别取刀间距6，8，10 mm 以及12 mm进行滚刀协同破岩仿真，滚刀破岩形成的轨迹如图2所示。 由图1 可以看出，不同刀间距下的滚刀协同破岩效果存在明显的区别，在给定的滚刀、岩石参数以及切深2 mm 的情况下，刀间距8 mm 时的破岩仿真效果较好， 相邻滚刀之间的破坏区域会相互重合，满足滚刀协同破岩要求。 同样地，刀间距6 mm 也可达到了较好的破岩仿真效果，但是刀间距太小会使破坏区域过度重合， 造成破岩能量的浪费。 刀间距10 mm 和12 mm 的破岩效果相对不太理想，随着刀间距增大，其滚刀之间的岩脊就会越明显。

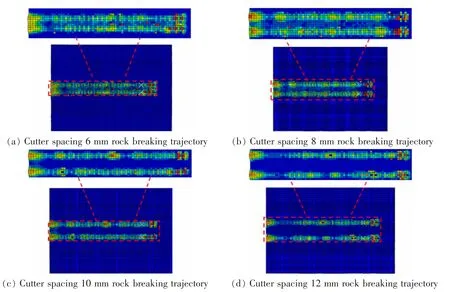
图2 不同刀间距下滚刀协同破岩轨迹Fig.2 Collaborative rock breaking trajectory of disc cutters under different cutter spacing

图3 为不同刀间距下的滚刀协同破岩的滚动力变化曲线，可以看出，滚刀1 和滚刀2 所受滚动力在整个切削过程中呈现出阶段式波动，并且两滚刀所受滚动力的变化曲线大致上完全相等，但是难以对比在不同刀间距下的滚刀进行协同破岩时所受的滚动力大小以及变化情况。

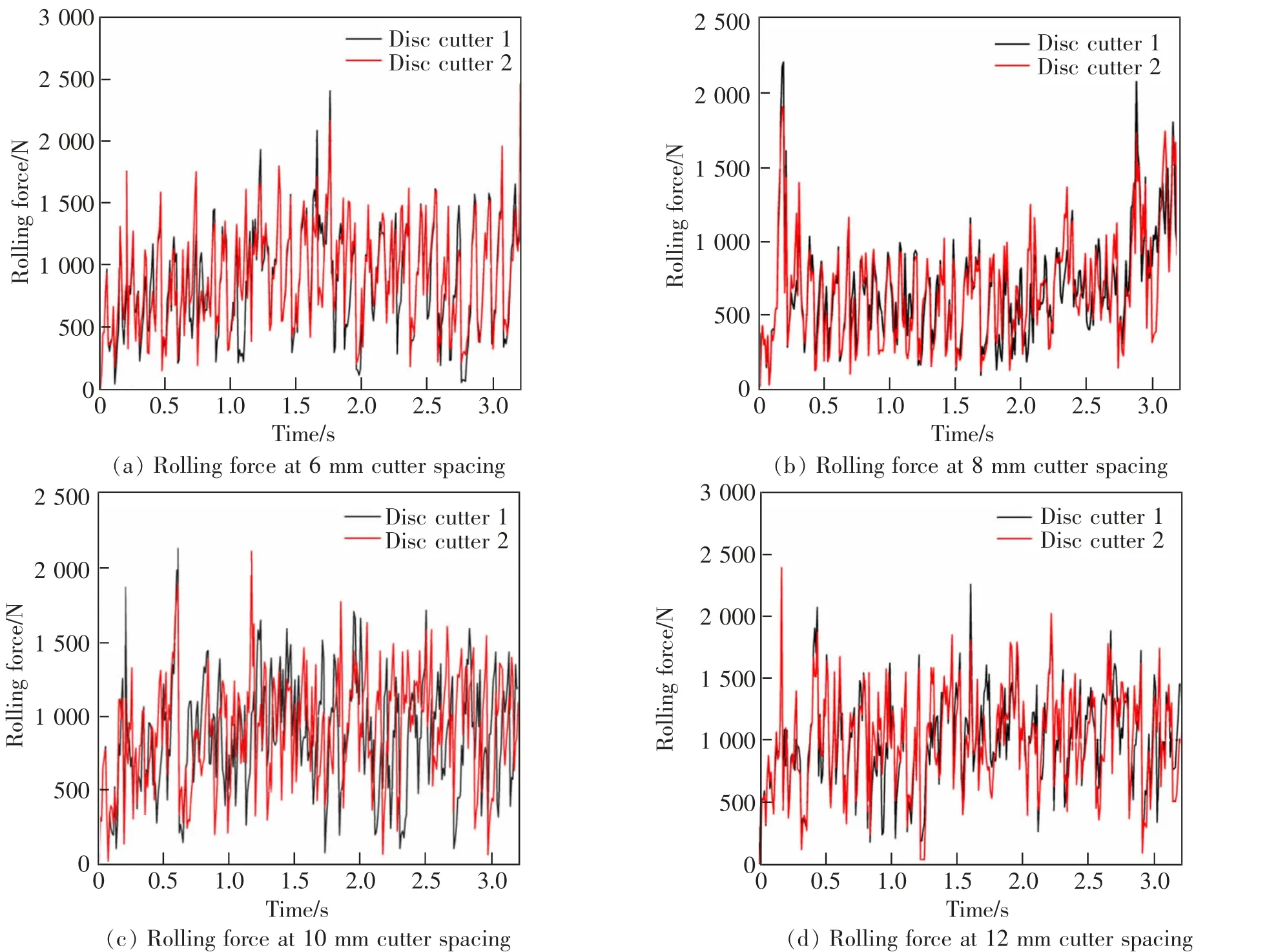
图3 不同刀间距下滚刀协同破岩的破岩力变化曲线Fig.3 Variation curves of collaborative rock breaking force of disc cutters for rock breaking under different cutter spacing

为了解不同刀间距的滚刀进行协同破岩时其滚动力变化情况，取滚刀滚动力在不同刀间距下的平均值进行对比，如表1 所示，可以看出不同刀间距下的平均滚动力会有明显差异，其滚动力并不是随着刀间距增大而不断增加，而是在刀间距8 mm 时出现了最低值。 这是因为在合适的刀间距下，滚刀之间协同破岩能使岩石内部产生更多裂纹，从而更容易破碎，那么岩石体对滚刀的反作用力也就减小，而过密的刀间距会导致滚刀之间作用区域重复，对于岩石的岩渣未能有效清除而导致再次作用， 致使刀间距6 mm 比8 mm的滚动力要大，在刀间距超过8 mm 时，其平均滚动力随刀间距的增大而逐渐增加，说明两滚刀之间作用区域的裂纹未连接或者连接的裂纹不足以让两刀之间岩石破碎形成岩渣，相邻滚刀之间只能各自形成切割凹槽，从而两条破岩轨迹之间出现岩脊现象。

表1 不同刀间距下的破岩力平均值Tab.1 Average value of breaking force under different disc cutter spacing

对于滚刀的布置一般呈现螺旋线排列， 考虑到刀盘中心区域需布置中心刀具以及刀盘驱动轴承，刀盘的中心区域直径定为150 mm，滚刀初始半径定为80 mm，刀间距为8 mm，相邻滚刀之间距离是相同的，但是不同辐条的第1 个滚刀距离刀盘中心的距离是不同的，滚刀螺旋线按逆时针布置，则按逆时针第1 个滚刀距离刀盘中心分别为80，88，96，104 mm，每个辐条滚刀相距32 mm，则可知上、下以及左辐条布置5 个滚刀，而右边辐条布置6 个滚刀。

2.2 整体刀盘结构的切刀设计

切刀作为盾构模型机以及后续模型试验最重要的刀具之一，也是数量最多的切削刀具，其布置是否合理将直接影响到刀盘的切削效率，对后续模型盾构机的模型试验精确性起决定性作用。 布置切刀的核心要求在于中心刀与切刀相互配合，其切削轨迹需布满整个刀盘面，对于本次切刀的安装主要分布在刀盘开口的两侧，对称布置，可直接对土体进行切削。 目前来说，布置切刀主要有同心圆布刀法、阿基米德螺旋线布刀方法以及单罗马螺旋线布刀方法等3 种主流方法[19]。

2.2.1 基于同心圆布刀法设计

采用同心圆布刀方法时， 考虑到刀盘中心区域需布置中心刀具以及刀盘驱动轴承等影响以及考虑到后续拆卸安装问题， 中心区域直径定为150 mm，设切刀初始半径为70 mm， 刀间距为15 mm，切刀刀宽为30 mm，周边刮刀刀宽25 mm，则通过计算可知，切刀在各辐条的布刀位置距刀盘中心点分别为70，115，160，205，250 mm，其中每个辐条两侧对称布置，则可知左右的辐条两侧分别布置3 把，位置为70，160，250 mm，而上下的辐条两侧分别布置2 把，位置为115，205 mm，如图4（a）所示。

2.2.2 基于阿基米德螺旋线布刀法设计

由于刀盘整个空间的有限性，阿基米德螺旋线只采用单螺旋线。 基于阿基米德螺旋线布刀法的计算，则可以得到刀盘正右方辐条的布刀位置距离刀盘中心分别为90，210 mm；正上方辐条的布刀位置距离刀盘中心分别为120，240 mm； 正左方辐条的布刀位置距离刀盘中心分别为150，270 mm； 正下方辐条的布刀位置距离刀盘中心为180 mm， 共7把切刀，本着切刀正反对称布置原则，即刀盘面板上的切刀数为14 把， 左右分别4 把， 上下分别3把，如图4（b）所示。

2.2.3 基于单费马螺旋线布刀法设计

根据单费马螺旋线在刀盘面板上布置切刀时首先要确定刀盘直径以及周边刮刀的布置位置，从而确定切刀数量、刀宽以及布置位置。 基于单费马螺旋线布刀法的计算，则可以得到刀盘正右方辐条的布刀位置距离刀盘中心分别为100，224 mm；刀盘正上方辐条的布刀位置距离刀盘中心分别为142，245 mm； 正左方辐条的布刀位置距离刀盘中心分别为174，265 mm；正下方辐条的布刀位置距离刀盘中心为200 mm，共7 把切刀，本着切刀正反对称布置原则， 即刀盘面板上的切刀总数为14 把，其中左右分别4 把，上下分别3 把，如图4（c）所示。

图4 基于不同布刀方法的刀盘模型Fig.4 Cutterhead model based on different methods of arranging cutters

3 刀盘模型动态仿真分析

3.1 刀盘数值模型建立

为对比上述3 种切刀布置方法的刀盘结构优劣，进行掘削动态仿真分析。 主要比较3 种切刀布置方法的优劣，判断是否合理；因此在刀盘上暂不布置滚刀，仅考虑布置切刀、周边刮刀以及中心刀。 通过SolidWorks 软件对盾构模型机的刀盘进行三维建模，在不影响刀盘整体结构强度的前提下， 可做以下简化处理：

1） 删除刀盘面板上所有的螺栓式结构，假定直接连接在刀盘面板上；

2） 删除滚刀及刀座， 并且仅保留一边切刀、周边刮刀以及中心刀；

3） 删除刀盘的倒角、圆角等复杂部位，便于后续网格划分。

刀盘的材料采用Q345 钢，并采用线弹性模型，其中刀盘模型采用C3D8R 单元，单元总数为64 222，土层选用滨海地层的粉质粘土，采用扩展的D-P 模型，其中土体模型同样采用C3D8R 单元，单元总数为108 425 个。 在刀盘旋转切削掌子面土体这一动态仿真过程中，引用单元失效准则模拟土体的切削分离过程，从而分别检验基于同心圆布刀法、阿基米德螺旋线布刀法和单费马螺线布刀法的切刀切削轨迹以及结合中心刀、周边刮刀的切削轨迹能否满足切削整个掌子面的设计要求。

3.2 基于动态仿真结果的刀具布置优选

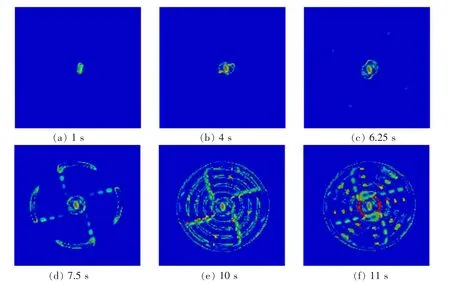
图6 阿基米德螺旋线不同时刻刀盘切削土体动态图Fig.6 Dynamic diagram of soil cutting by cutterhead at different time with Archimedean spiral

图5～图7 分别为基于同心圆布刀法，阿基米德螺旋线布刀法，单费马螺旋线布刀法的切刀组合中心刀，周边刮刀在不同时刻的土体切削动态图。 其中在0～6.25 s 这一时间段内，都是中心刀具先与土体直接接触，对中心区域土体进行旋转切削并产生塑性变形，随后与待开挖土体分离形成渣土，退出后续模型计算；在6.25～7.5 s 这一时间段内，周边刮刀开始切削土体并逐渐确定整个待切削面的范围，由于中心刀具、周边刮刀布置位置均相同，在0～7.5 s 这一时间段内，3 种布置方法的切削效果表现完全一致；在T=7.5 s 时切刀开始与土体接触，随着刀盘继续推进、旋转，此时待切削面的土体被分成四部分先后切削，切削后的土体会逐渐重合；在T=10 s 时，刀盘旋转切削一圈，此时开挖面土体已被全面切削， 而当T=11 s 时已进入下一个循环周期。 从土体的切削分离状态来看，可以发现阿基米德螺线和单费马螺线的刀具布置方法均能实现土体的全面切削，同心圆布置法存在切刀之间不完全切削现象，不满足使用要求。

图5 同心圆布置法不同时刻刀盘切削土体动态图Fig.5 Dynamic diagram of soil cutting by cutterhead at different time with concentric circle arrangement method

图7 单费马螺线不同时刻刀盘切削土体动态图Fig.7 Dynamic diagram of soil cutting by cutterhead at different time with single Fermat spiral

在整个刀盘旋转切削的数值仿真中，可知只对比待开挖面土体的切削分离状态是无法甄别最优布刀方法的， 而对于在整个切削过程中刀盘荷载随着时间的变化规律也是一个重要考量因素。3 种布刀方法的刀盘结构在整个动态仿真过程中所受荷载随时间的变化曲线如图8， 图9 所示。

图8 不同结构刀盘随时间对应刀盘推力曲线图Fig.8 Curves of cutterhead thrusts of different structure cutterheads over time

从图8，图9 中均可以看出，在0～6.25 s 的这一时间段内，只有中心刀具在对中心区域的土体进行旋转切削，刀盘的推力、扭矩随着中心刀具不断深入而缓慢增加；在6.25～7.5 s 这一时间段内，周边刮刀开始进行切削工作，逐渐形成整个刀盘的掌子面切削范围，此阶段内的中心刀具以及周边刮刀进行旋转切削，刀盘的推力、扭矩会有一定的明显上升趋势；在7.5～10 s 这一时间段内，这时刀盘面板上数量最多的切刀开始与土体接触，此阶段刀盘上切刀、中心刀以及周边刮刀都对整个待切削面进行旋转切削，在这一时间段内的刀盘推力、扭矩开始陡然上升；在10 s 后，刀盘完成旋转切削一圈，刀盘的推力、扭矩均已达到最大值，此时所有的刀具都全部进入切削工作，由于采用了土体损伤失效分离准则，随着刀盘的推进、旋转，不断有已失效的土体退出计算以及切削新的待切削土体，从而使得刀盘的推力、扭矩开始处于上下波动的稳定状态，其变化趋势符合实际要求。

图9 不同结构刀盘随时间对应刀盘扭矩曲线图Fig.9 Curves of cutterhead torques of different structure cutterheads over time

将同心圆布刀法、阿基米德螺旋线布刀法以及单费马螺旋线布刀法得到的刀盘结构所受推力和扭矩进行汇总，如表2 所示。 根据理论计算得到的刀盘推力、扭矩值以及对比表2 可知，因为在动态切削仿真过程中未考虑到土层地应力以及埋深的影响，其仿真结果都比理论计算值要小。 其中单费马式的刀盘得到的最大以及平均推力、扭矩相对阿基米德式、同心圆式的刀盘均要小，说明单费马螺旋线布刀方法要优于另两种，能有效减少刀盘所受荷载。 本着刀盘整体受力情况最好的设计原则，选用单费马螺旋线布刀法在刀盘面板上布置相应的切刀。

表2 不同布刀类型的刀盘荷载情况Tab.2 Load situation of cutterheads of different layout types

4 刀盘结构受力性状分析

由图10（a）～图10（c）可以看出，正常推进工况下的刀盘最大应力为61.03 MPa， 最大推力工况下的刀盘最大应力为118.7 MPa， 以及最大扭矩工况下的刀盘最大应力为18.53 MPa，都小于Q345 材料的许用应力；由图10（d）～图10（f）可以看出，正常推进工况、最大推力工况以及最大扭矩工况下的刀盘最大位移量分别为0.36，0.228 mm 和0.617 mm，位移量都比较小，刀盘结构几乎没有变形。 综合考虑盾构模型机的刀盘在动载荷下的载荷分析和静载荷下的应力应变分析，基于单费马螺旋线布刀法的刀盘满足全面开挖掌子面土体的要求，以及其整体强度、刚度均能够满足一般机械使用要求，刀盘大部分区域应力均相对较小，只有极小部分区域应力相对较大，但都小于材料的许用应力，并且各个工况下刀盘变形均相对较小，几乎可忽略不计，可直接进行生产加工制作实物。

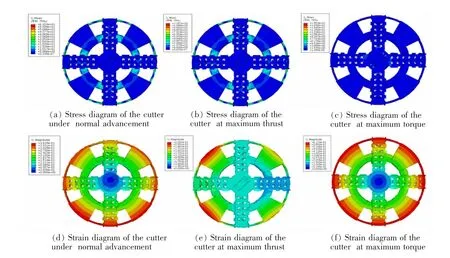
图10 3 种工况下刀盘应力应变图Fig.10 Stress and strain diagram of cutterhead under three working conditions

5 结论

本文针对滨海复合地层的地质特征，对微型盾构机刀盘进行了优化设计。 主要结论如下：

1） 双滚刀协同破岩仿真过程中，滚动力并不是随着刀间距增大而不断增加， 在刀间距8 mm 时出现最低值，表明在合适的刀间距情况下，滚刀协同破岩会导致岩石内部产生更多裂纹，从而更容易破碎，可提高破岩效率。

2） 基于阿基米德螺线和单费马螺线布刀法的刀盘均能满足掌子面全开挖的要求，同心圆布刀法刀盘切刀之间存在不完全切削现象；3 种刀盘结构的动态仿真过程中，0～7.25 s 阶段主要由中心刀和周边刮刀切削土体，推力、扭矩变化曲线基本一致，7.25 s 以后切刀开始和土体接触， 土体被分成四部分先后切削，切削后的土体会逐渐重合并形成同心圆，推力、扭矩均急剧上升，10 s 以后刀盘完成旋转一圈，推力、扭矩均达到最大值；最终根据刀盘整体切削效果以及推力、扭矩大小，确定单费马螺旋线布刀法为最优布刀方案。

3） 考虑微型盾构机掘进的正常工况、最大推力工况以及最大扭矩脱困工况，针对单费马螺旋线布刀法的刀盘结构强度与刚度进行验算，结果表明其应力强度均满足要求，变形位移分别为0.36，0.228，0.617 mm，满足一般工程机械使用要求。