折流角变化下的旋流式竖井溢洪道涡室脉动压强试验研究

苟 超，杨红宣，沈春颖，赵国安，马江霞

（昆明理工大学电力工程学院，昆明 650000）

0 引 言

旋流式竖井作为一种新型高效的泄流消能工，主要是利用水流在竖井段的螺旋运动和底部消力井段的强烈紊动以达到消能的目的。与传统泄流消能工相比，旋流式竖井因具有适应性强、布置方便、施工简单及消能率高等特点而被水利工程广泛应用，如溪洛渡、双沟、小湾及沙牌水电站［1，2］等均采用旋流式竖井消能，高水头、大泄量是这些水利工程具有的共同特点之一。高水头泄水建筑物泄流时容易受高速水流作用使其结构遭到破坏的问题，这不仅与时均压强有关，而且很大程度上与脉动压强的特性有关，当水流脉动频率与泄水建筑物自振频率相近时，容易引发建筑物共振从而造成结构破坏。因此不少学者对旋流式竖井的压强特性做了许多研究工作并取得了一些成果。李庆生［3］通过水工模型试验对旋流式竖井涡室、侧壁及底板的压力变化规律进行了研究，提出了以冲击压力作为消力井底板失稳的标准。陈小威［4］通过改变消力井井深分析其对消能井底板压强、脉动压强参数、压坡段压强的影响，得出了各部位时均压强和脉动压强的变化规律。何军龄等［5］通过物理模型试验对不同衔接段体型下竖井底板脉动压强的影响进行了研究，试验结果表明：消能井底板最大脉动压强与压坡出口面积呈正相关，加深消能井深度及延长压坡长度等措施均不能降低竖井底板的最大脉动压强。综上所述，前人对旋流式竖井在竖井结构尺寸变化对消能井底板及侧壁压强的影响方面研究较多，但对旋流式竖井涡室压强特性方面的研究还不够完善，实际上，水流进入涡室后流线连续急剧转向，流态十分复杂；另外，水流在涡室螺旋下泄时携入大量气体加剧了水流的紊动，其压强特性又区别于其他部位。鉴此，本文借助水工模型试验方法研究不同折流角及下泄流量下的旋流式竖井涡室脉动压强幅值特性、脉压强度及频谱特性，研究成果旨在进一步为旋流式竖井体型设计防护提供参考。

1 模型试验布置

由于本文重点研究涡室压强的变化规律，故仅给出竖井上段的试验模型图见图1。引水道为明渠矩形段，断面尺寸由18 cm×22 cm（宽×高）渐变为15 cm×22 cm，长度（指进水口至涡室进口处）为230 cm，底坡坡度为i=5%。引水道末端左侧通过由长轴为38 cm 短轴为22 cm 的1/4 椭圆曲线（ab 段）与涡室消能竖井相接，右侧为折流坎（cd 段），已有资料［6］表明折流坎与引水道边墙的夹角在10°以内，故试验中分别采用折流角θ=0°（即无折流坎）、3°、4.5°共3 种折流坎。涡室直径为D1=20 cm，高度为50 cm，竖井直径为D=15 cm，竖井高度为194 cm，在涡室边壁设B1～B10 共10 个测压孔，其位置在图示xyz坐标系（坐标单位cm）中为B1（10，0，9）、B2（10，0，14）、B3（10，0，20）、B4（0，10，9）、B5（0，10，14）、B6（0，10，20）、B7（-10，0，3）、B8（-10，0，6）、B9（-10，0，10）、B10（-10，0，18）；为便于试验观测，模型从引水道至竖井后的出水段全部均采用8 mm的有机玻璃制作。

试验中，下泄流量供给采用三角形薄壁堰控制，水位采用精度为0.1 mm 的测针测量，测点脉动压力利用CY200系智能数字压力传感器进行数据采集和处理，采样间隔为0.02 s，采样容量N=1 500，用时30 s。测点时均压强利用玻璃测压管及精度为1 mm的钢板尺测量。

2 试验结果及分析

2.1 折流坎折角对脉压强度的影响

水流经过引水道流入涡室后由于边界条件发生改变，流线连续急剧转向，加剧了水流与涡室壁面的碰撞，水流十分紊乱，常规的分析方法已不能准确详细地描述该部分水流的紊动特性，脉动压强均方根σ能较好地反映各测点部位所受水流脉动荷载的瞬时性［7］。本文引入无量纲化参数—表征水流紊动强弱特性的脉压强度β、反映折流坎折角大小的过流断面收缩系数ξ，计算公式分别如下：

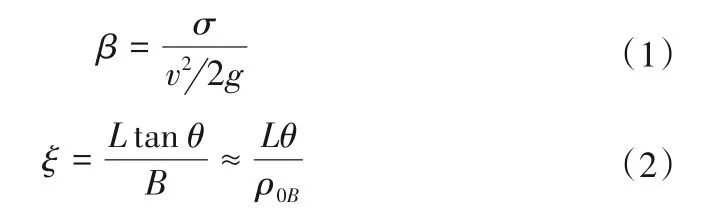
式中：tanθ≈θ、ρ0≈57.3°；σ为脉动压强均方根，kPa；v为涡室进口断面平均流速，m/s；g为重力加速度；L为折流坎至引水道与涡室连接处的距离（m）见图1；θ为折流坎折角，°；B为引水道末断面底宽，m。

为了研究折流坎折角变化对涡室脉压强度的影响，将下泄流量进行无量纲化处理得到下泄流量参数Q2/gD5（Q为下泄流量，m3/s；D为竖井直径，m），试验实测了3 种折流坎折角在4 种不同流量参数Q2/gD5=0.09、0.19、0.26 和0.34 下的脉动压强，由试验结果计算出脉压强度在不同折流坎折角下的变化规律，见图2示。从图2可以看出：在不同折流坎折角下，涡室脉压强度在4 种泄流量下的分布规律基本一致，脉压强度随测点位置的不同而不同且最大值均出现在B7 测点位置处。另外，在不同泄流量下，脉压强度随折流坎折角的增大而增大。这主要因折流坎折角增大导致涡室进口处过流面积减小，从而间接导致进口流速增大，使得水流与边壁的相互作用增强，加剧了水流的紊动，这一点也可以从脉动压力时间过程线中看出，见图3示。说明增大折流坎折角可以有效提高旋流式竖井的消能效果。

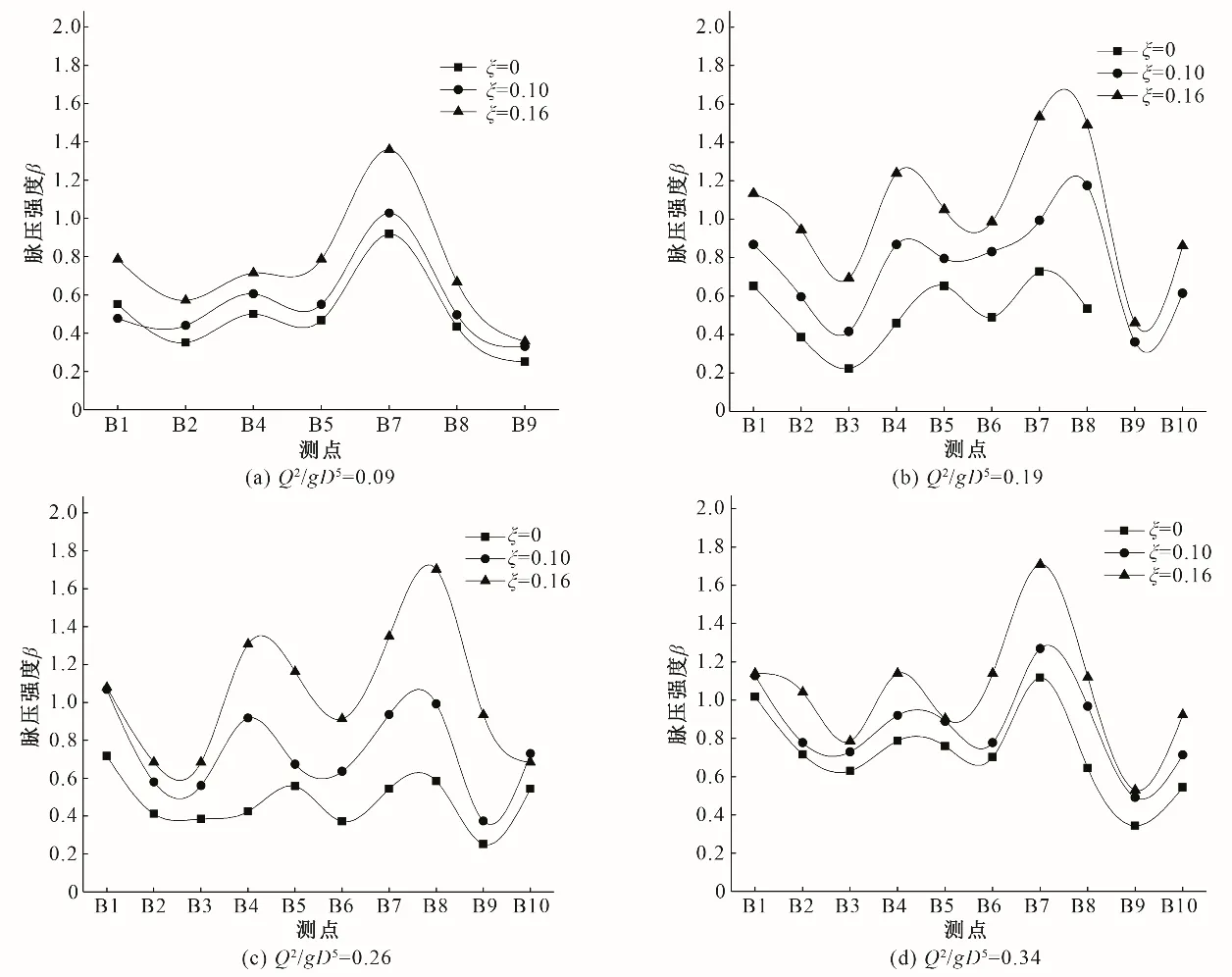
图2 不同流量下涡室脉压强度βFig.2 Flow fluctuating pressure β in vortex chamber at different flow rates

图3 不同流量下脉动压力时间过程线图Fig.3 Time process diagram of fluctuating pressure under different flow rates

2.2 折流坎折角对概率密度的影响

脉动是一个随机的过程，脉动序列的正态性是研究脉动压强比较关注的问题［8，9］，概率密度函数可以直观反映出脉动压强振幅的分布特性，目前一致认为：水流脉动压强振幅的概率密度符合正态分布［9］。而概率密度函数是否服从正态分布可以通过计算脉动压强的偏态系数CS和峰态系数CE来判别。

偏态系数：

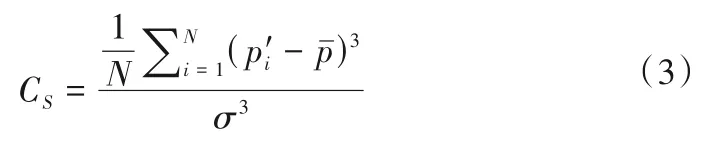
峰态系数：

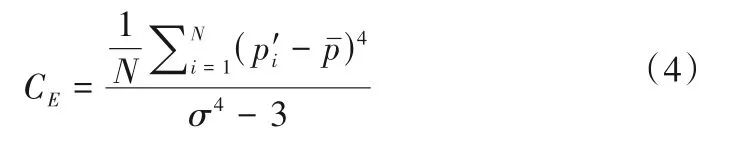
偏态系数CS是随机变量相对于平均值不对称程度的度量，能够反映随机变量的偏离程度及方向，若偏态值等于0，概率密度为正态分布，偏态值大于0，分布曲线较正态分布偏左，概率密度为正偏分布，偏态值小于0，分布曲线较正态分布偏右，概率密度为负偏分布。而峰态系数CE是概率密度分布曲线相对于正态分布平峭程度的度量，若峰态值大于0，分布形态陡峭（瘦高型），峰态值小于0，分布形态平缓（矮胖型）。

试验实测了不同折流坎折角和不同流量下的脉动压强，并将脉动压强进行标准化处理，经标准化后的脉动压强概率密度如图4所示，从图4可以看出；在不同折流坎折角下，概率密度在各泄流量下的分布规律基本一致且接近正态分布，脉动压强的偏态系数主要集中在0 附近上下波动，概率密度出现正偏和负偏的机率大致相等，峰态系数随折流坎折角的增大有所减小，说明概率密度分布较对称且属于低峰态分布。另外，在不同泄流量下，概率密度随折流坎折角的增大而变得更加平缓，概率密度分布曲线较标准正态分布曲线更加矮胖，脉动压强振幅较大。说明增大折流坎折角可以有效增加脉动幅值范围，水流的脉动程度明显加剧，较大的紊动运动可消耗大量的能量，这也是旋流式竖井消能的关键所在，进一步说明适当增加折流坎折角可以提高旋流式竖井的消能效果。

图4 典型测点（B7）在不同流量下的概率密度及偏态、峰态系数Fig.4 Probability density，skewness and kurtosis coefficients at a typical measurement point（B7）under different flow rates

本实验还计算了在流量参数Q2/gD5=0.19、0.34 条件下由折流坎折角变化引起的压强偏态系数和峰态系数变化值，见表1、2 所示。由计算结果可知，在不同流量和不同折流坎折角下涡室各测点脉动压强偏态系数CS值集中在-0.2～0.2之间，峰态系数CE值分布在-0.3～0.3 之间。为了能够清晰地展现出偏态系数和峰态系数与折流坎折角之间的关系，把表1、2 中数据绘制成图5所示。

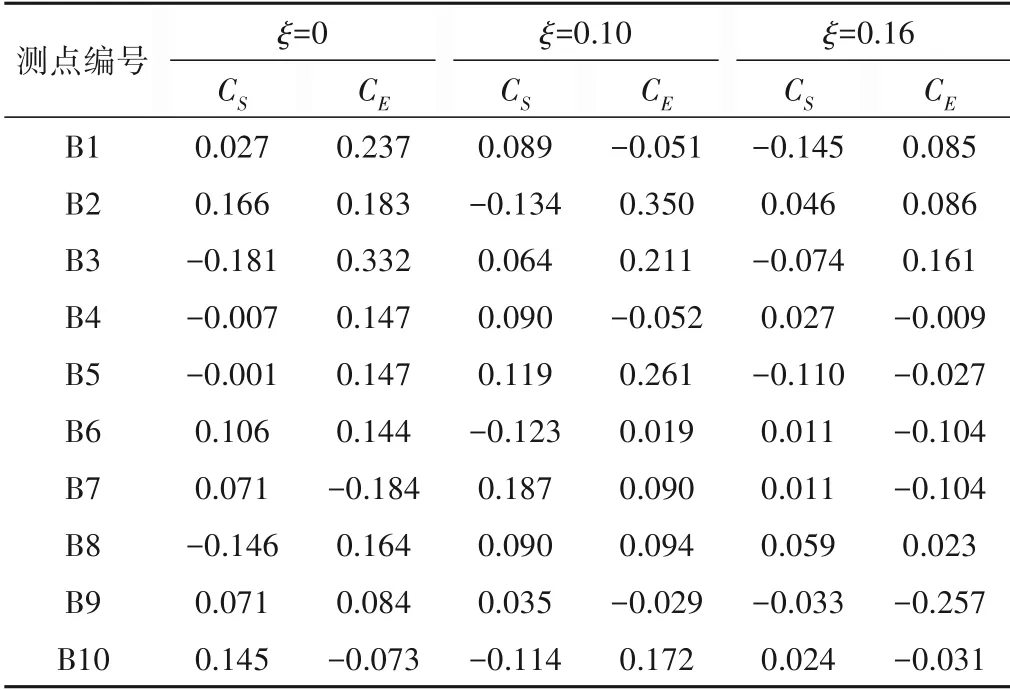
表1 Q2/gD5=0.19下脉动压强的偏态系数和峰态系数Tab.1 Skewness coefficient and kurtoshi coefficient of fluctuating pressure at Q2/gD5=0.19

从图5可以看出，不同流量下，涡室各测点的脉动压强偏态系数主要围绕在零附近上下浮动，偏态值接近于零，与折流坎折角的相关性较弱，峰态系数总体上随折流坎折角的增大而有所减小，概率密度分布从瘦高型逐渐向矮胖型发展，涡室各测点脉动压强的概率密度分布基本符合正态分布，但又都不服从标准正态分布。

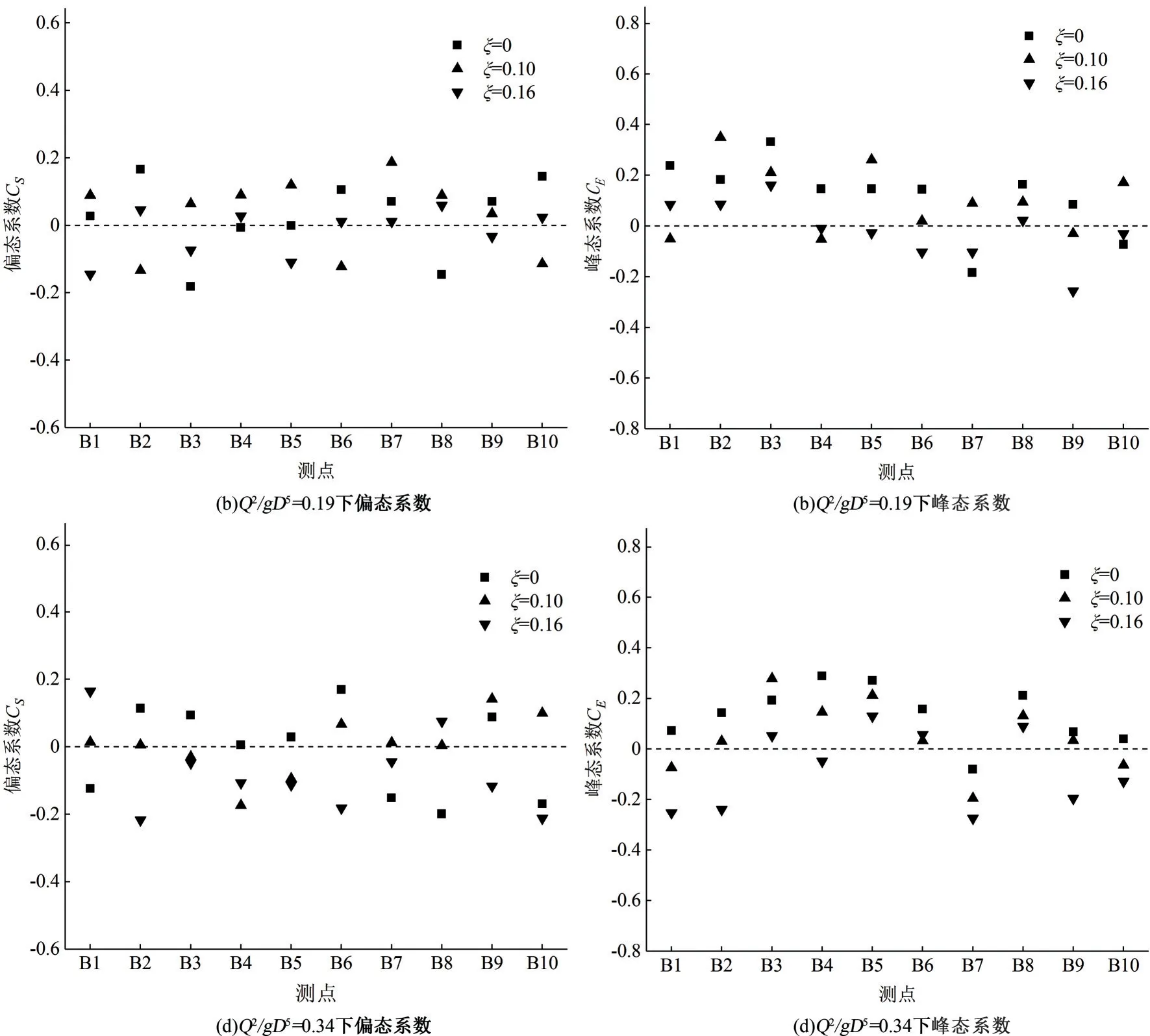
图5 不同流量下的偏态系数和峰态系数Fig.5 Skewness coefficient and kurtosis coefficient at different flow rates

2.3 折流坎折角对脉动压强频谱特性的影响

水流的脉动是由许多不同尺度、不同强度、旋转各异的涡旋相互混掺、碰撞作用导致的结果，壁面压强的脉动也是涡旋与边界相互作用的反映［10］。本文通过对采集后的涡室脉动压强进行归一化处理，并将归一化后的值进行快速傅里叶（FFT）变换，将时域信号转换成频域信号，从而可以获得用于反映脉动压强能量分布情况的归一化功率谱密度。

表2 Q2/gD5=0.34下脉动压强的偏态系数和峰态系数Tab.2 Skewness coefficient and kurtosis coefficient of fluctuating pressure at Q2/gD5=0.34

脉动压强归一化可以表示为：

连续时间信号f(t)的傅里叶变换可以表示为［11］：

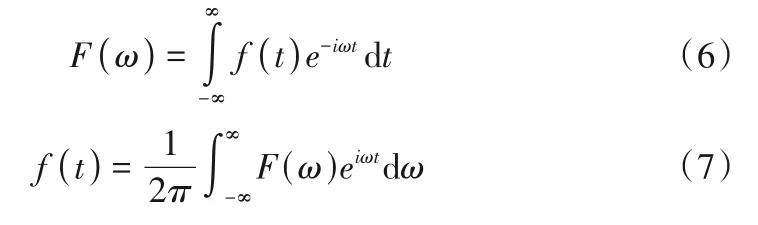
式中：ω为脉动压强系数；p为脉动压强，kPa；pˉ为脉动平均压强，kPa；ρ为水的密度，kg/m3；v0为出口流速，m/s。

水流的脉动压强是由一系列具有能量的频率分量组成的，功率谱密度则反映了频率分量的平均值［11］。已有的研究表明：水流的紊动能量主要集中分布在0～20 Hz 范围内，一般将0～2 Hz称为低频范围，2～20 Hz称为主频范围，而将大于20 Hz称为高频范围［11，12］。图6为不同流量下涡室典型测点的脉动压强归一化功率谱密度图，从图6可以看出，在不同流量下，脉动压强的能量主要集中分布在0～40 Hz 范围内且随泄流量的增大脉动能量分量在其范围内明显增多。在相同水力条件下，脉动压强主频率随折流坎折角的增大其频率范围有所拓宽并逐渐向高频转移，脉动能量主要由高频大尺度涡旋决定，水流紊动加剧，壁面脉动压力增大，高频率脉动相对泄水建筑物自振频率发生同步的可能性较大，应引起足够重视。

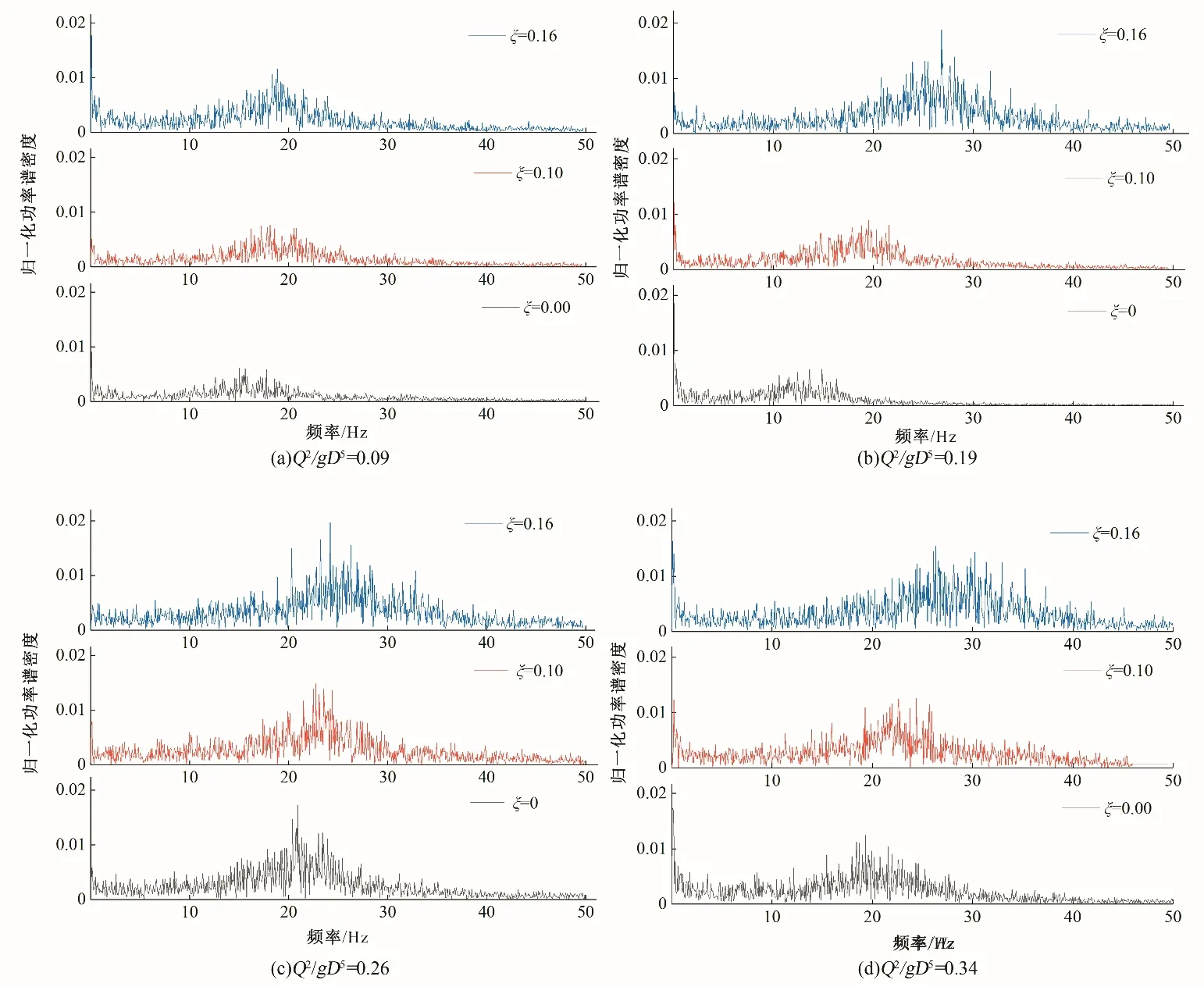
图6 不同流量下典型测点（B7）的功率谱密度图Fig.6 Power spectral density of typical measuring point（B7）at different flow rates

3 结 论

基于水工模型试验，研究了折流坎折角和下泄流量对涡室脉动压强分布规律的影响，得到以下结论：①相同流量下的脉压强度随折流坎折角增大而增大且分布规律基本一致，同一折流坎折角下的脉压强度随流量同步增减，脉压强度与能量耗散密切相关，脉压强度越大能量耗散越快。②不同流量下的脉动压强概率密度符合正态分布，偏态系数主要集中分布在-0.2～0.2 之间，与折流坎折角的相关性较弱，峰态系数集中在-0.3～0.3 之间，出现正偏和负偏的几率大致相等。此外，相同水力条件下，随着折流坎折角增大，概率密度分布较标准正态分布更加矮胖，脉动幅值范围增大，水流紊动程度加剧。③脉动压强振幅随流量增大而增大，脉动能量主要集中分布在0～40 Hz以内，脉动优势频率随折流坎折角增大其主频率带有所拓宽并向高频转移，脉动能量主要由高频大尺度涡旋决定，脉动能量对建筑物的荷载作用引应起足够重视，在不产生共振的条件下，适当增加折流坎折角对提高旋流式竖井的消能效果是有利的。