基于均匀试验和PSO-RBF的均质库岸边坡可靠度预测模型
2022-07-27俞社鑫潘建平
俞社鑫,潘建平,2
(1.江西理工大学土木与测绘工程学院,江西 赣州 341000;2.江西省环境岩土与工程灾害控制重点实验室,江西 赣州 341000)
0 引 言
库岸边坡在运行周期内可能经历各种环境变化,受外界因素扰动会产生失稳,诱发滑坡灾害[1]。特别是三峡地区的库岸边坡在地震作用下产生较大变形发生失稳或者出现一些“震裂山体”,会降低岩土体的物理力学性质,另外随着水库水位的上升,地下水位会有所抬高,而水的软化作用同样也会降低岩土体的物理力学性质[2,3]。胡孝洪等[4]指出库水位下降导致坡体内水压力变化是边坡失稳的主要诱因;陈纪昌[5]通过某红岩泥质岸坡发现地震动荷载是其发生破坏的直接驱动力;王立纬[6]指出在库水位骤降与地震组合工况下,两岸堆积体易发生失稳。可见地震作用下或库水位变化会增加库岸边坡失稳几率,且两者同时存在,其稳定性会进一步显著降低,但目前研究大多是定性或定量分析,在不确定分析如可靠度研究领域较少。
岩土体土性参数是边坡失稳的主要内部因素,在分析中通常把土性参数如黏聚力、内摩擦角等看作确定性因素,而工程中这些因素是趋向于服从某种概率分布的随机变量[7]。鉴于此,边坡安全问题逐渐采用概率分析理论,使分析结果更符合客观实际,但相关方法均存在一些不足,如中心点法精度较低[8],尽管蒙特卡罗模拟法(Monte Carlo Simulation,MCS)精度较高但其计算量很大[9]。近年来,基于替代模型的可靠度分析方法越来越受到人们的重视,将复杂的隐式功能函数显式化,大大提高边坡稳定可靠度的计算效率[10]。人工神经网络因其强大的并行分布式处理、非线性映射、自适应和自组织学习能力,在工程领域得到了广泛的应用[9,10]。如王小兵等[7]采用正交试验得到样本点及试验值,基于反向传播(Back Propagation,BP)神经网络建立了堤防边坡失稳预测模型;何永波等[11]提出一种基于ABAQUS 和粒子群优化径向基函数(Radial Basis Function,RBF)神经网络的可靠度分析方法,建立了边坡可靠度指标和失效概率的预测模型;高傑等[12]基于RBF 神经网络,建立了红黏土锚固体界面的蠕变模型;舒苏荀等[13]选用拉丁超立方抽样法(Latin Hypercube Sampling,LHS)和有限元强度折减法产生样本点,基于RBF 神经网络建立了边坡安全系数和失效概率的预测模型。
本文在选取RBF 神经网络时为防止因参数选取不当对其预测精度产生过大影响,用有全局搜索能力的粒子群算法(Particle Swarm Optimization,PSO)对该网络参数进行优化。由于单靠稳定性系数不能准确反映库岸边坡所处状态,在考虑土性参数不确定性、几何参数以及地震作用和库水位变化等影响下,通过均匀试验设计法产生实验样本,通过PSO-RBF 神经网络建立了均质库岸边坡可靠度预测模型,在提高库岸边坡可靠度分析的效率的同时对相关工程稳定性的预警和灾害防治有一定参考价值。
1 均匀试验设计与PSO-RBF神经网络理论
1.1 均匀试验设计
在多因素、多水平的试验组合时,我国数学家方开泰和王元[14]将数论与多元统计相结合,在正交设计基础上提出一种适用于多因素、多水平的试验设计方法。
均匀设计表用Ua(bc)或U*a(bc)表示,其中U表示均匀设计;a表示均匀设计的行数,即本次试验的次数;b表示因素的水平数;c为因素个数。U右上角有没有“*”代表两种不同类型的均匀设计表,且有“*”代表更好的均匀性。另外均匀设计也可采用拟水平法安排试验,如表1为因素A 和B 有3 个水平,因素C有2 个水平下得到的混合水平的均匀设计表U*6(64),表2为其使用表。
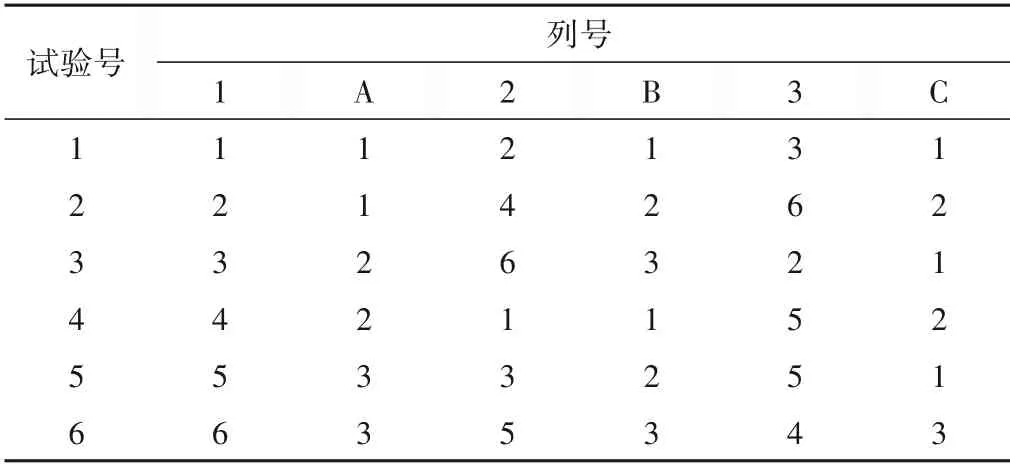
表1 混合水平的均匀设计表U*6(64)Tab.1 Uniform design table U*6(64)with mixed level
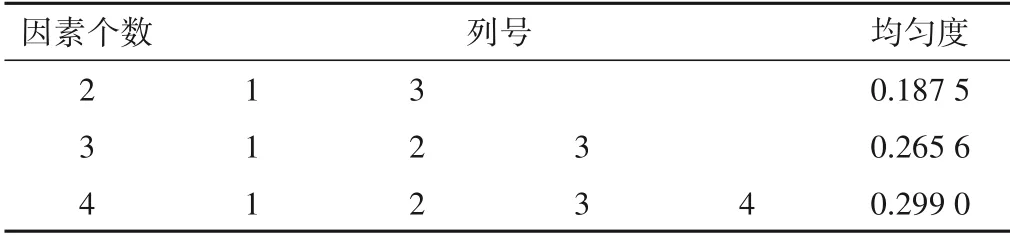
表2 U*6(64)的使用表Tab.2 The usage table of the U*6(64)
1.2 PSO-RBF神经网络理论
1.2.1 RBF神经网络
RBF 神经网络是一种性能优良的前馈型神经网络,能够以任意精度逼近非线性函数,具有全局逼近能力,收敛速度较快,根本上解决了BP网络的局部最优问题[9,15,16]。图1为一种典型RBF三层神经网络结构。
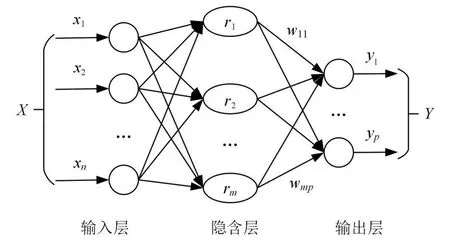
图1 RBF神经网络结构Fig.1 RBF neural network structure
设输入层神经元为X=[x1,x2,…,xn]T,隐含层神经元为R=[r1,r2,…,rm]T,输出层神经元为Y=[y1,y2,…,yp]T。当采用高斯函数时,隐含层中第i个神经元的作用函数Ri(X)表示为

式中:X为输入向量;Ci第i个基函数的中心,与X有相同维数的向量;σi为第i个基函数的宽度,m为隐含层节点数;‖X-Ci‖为向量X-Ci的范数,表示X与Ci间的距离。
输出层第k个神经元网络输出表示为:
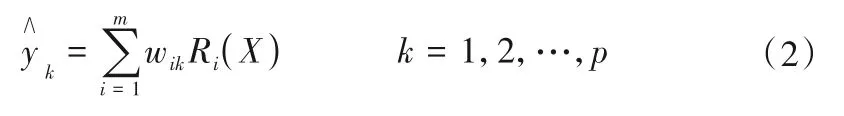
式中:n为输入层节点数;m为隐含层节点数;p为输出层节点数;wik为隐含层第m个神经元与输出层第k个神经元的连接权值。
由于网络预测效果十分依赖聚类中心Ci、权值wik及宽度σi三个参数,本文选用PSO 算法对以上参数进行寻优,以达到提高精度。
1.2.2 PSO算法
PSO算法是一种从群鸟觅食行为特征中得到启发而提出的搜索算法,既兼顾个体性和全局性,又能以更快的、更大的概率收敛于最优解[17]。假设在一个D维空间中有n个粒子的粒子群,算法会先初始化一群粒子,然后在每一次迭代过程中,粒子通过跟踪2 个极值(个体极值pi和全局极值pg)来更新自己的速度v和位置x,按下式(3)迭代,终止条件为设置的最大迭代次数。
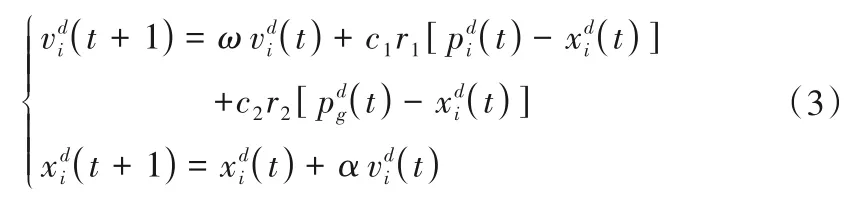
当前粒子的速度和位置;pdi==(p1i,p2i,…,)为当前粒子的个体极值;pdg=(p1g,p2g,…,pDg)为当前整个粒子种群的全局极值;c1和c2为非负加速常数;r1和r2是两个处于0与1范围内的随机数;α称为约束因子。具体步骤如下:
(1)初始化粒子群,赋予每个粒子随机的初始位置和速度;
(2)根据适应度函数,计算粒子的适应度值;
(3)分别计算每一个粒子当前位置和其个体极值、全局极值及与之对应的适应度值,并比较结果,若当前位置的适应度值更优,则使用当前位置更新个体极值pi和全局极值pg;
(4)根据公式(3)更新每个粒子的速度与位置;
(5)重复步骤(2)和(3),跟踪粒子的两个极值;
(6)若未满足结束条件,则重回步骤(4),若满足则算法结束。
2 均质库岸边坡可靠度分析
本文边坡可靠度分析主要包含边坡实验样本的参数生成、边坡整体可靠度分析以及PSO-RBF 神经网络对实验样本的训练与测试,具体分析过程见流程图2。
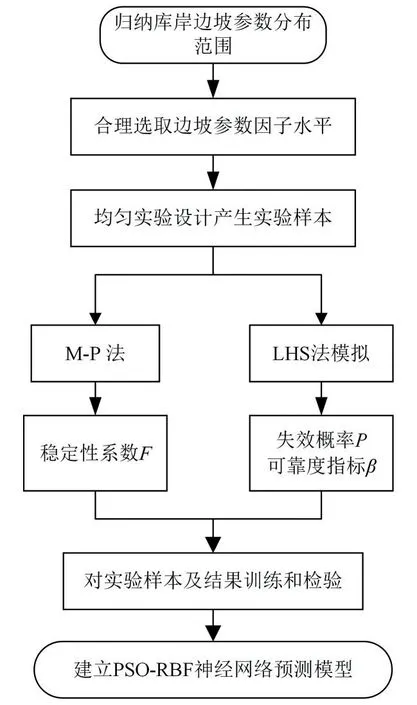
图2 库岸边坡可靠度分析流程图Fig.2 Flow chart of bank slope reliability analysis
2.1 实验样本的参数生成
为使建立的边坡模型具有一定的适用性,本文归纳库岸边坡土性参数、几何参数与外部因素的分布范围[18-20]见表3,表中参数C、φ和γ均服从正态分布,且不考虑相关性,在边坡可靠度计算时,各自均值和标准差可分别作为独立的输入变量。

表3 库岸边坡影响因素分布范围Tab.3 Distribution range of influencing factors of bank slope
2.2 边坡整体可靠度分析
建立均质岸边坡可靠度预测模型步骤:
(1)确定影响库岸边坡稳定的因素,根据实际情况及经验确定每一种影响因子的水平数,选用对应均匀试验设计表确定实验样本。
(2)依据表3边坡参数分布范围,利用Morgenstern-Price(M-P)法与LHS 法逐组求解实验样本的稳定性系数F、失效概率P及可靠度指标β。
(3)由均匀设计试验得到的实验样本及通过计算得到的结果分别对神经网络进行训练与检验,达到精度之后,将其作为均质库岸边坡可靠度的网络预测模型。
2.2.1 稳定性系数计算
当边坡体为相对均质体,可能发生圆弧滑动时,《水利水电工程边坡设计规范》(SL/386-2007)中推荐选用简化Bishop 和M-P 法计算都是可以的,另外M-P 法在确定边坡稳定性系数的同时还能较好地反映条块相互作用力以及最危险滑面的情况[21]。对于本文适宜选用M-P法,其过程详见规范。
2.2.2 可靠度指标计算
LHS 法有较好的一维投影和均匀分层分布特性,可均匀地覆盖到概率分布的上下限值,进行边坡可靠度分析时收敛速度要优于MCS法,其分析步骤相似[22,23]。
基本原理:在已知状态变量的概率分布类型前提下,依据边坡稳定的极限状态条件G(X1,X2,X3,…,XN)=1,产生符合变量分布的一组随机数x1,x2,…,xn,将其代入下列功能函数式(4),即可经过n次重复计算出N个相互独立的状态函数随机数。如假设n个状态函数随机数中有m个数小于等于1,那失效概率为Pf≈M N。

由这n个随机数得出稳定性系数F的分布特征(μF与σF);同时本文假设其为对数正态分布,可得边坡可靠度指标β即式(6)。
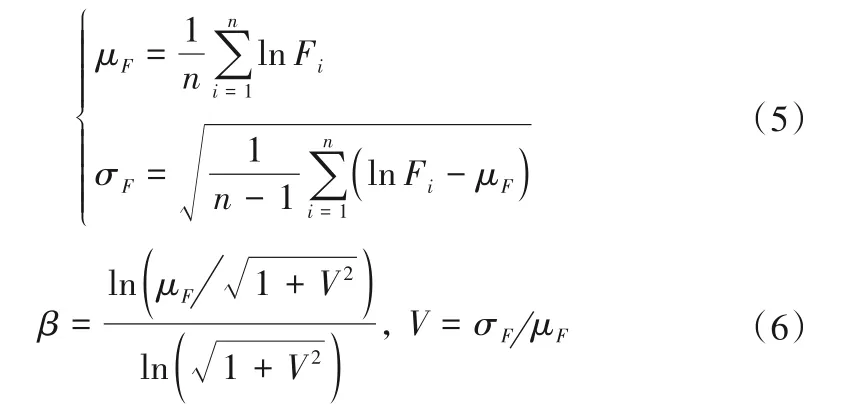
3 算例分析
3.1 边坡计算模型
结合表3中库岸边坡影响因素分布范围,采用图3中的二维边坡模型进行研究,其中Hmin=10 m,h为边坡库水位高度,a为水平地震加速度。
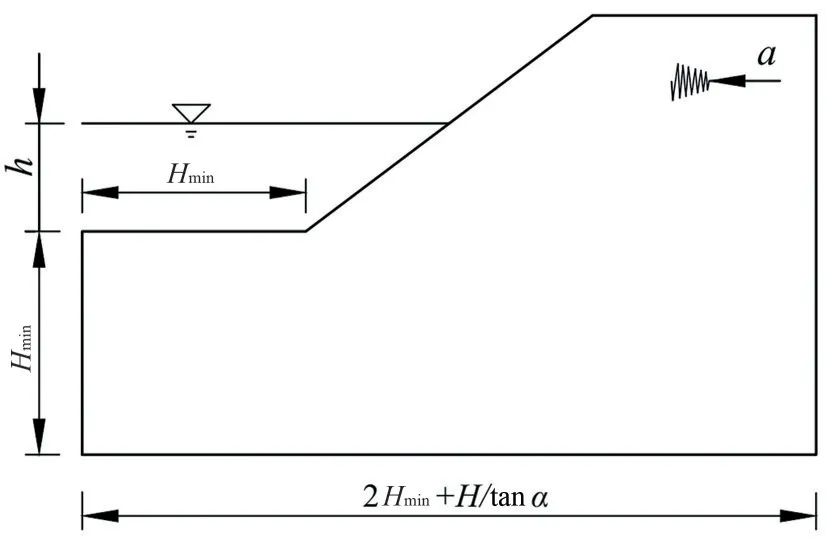
图3 二维边坡计算模型Fig.3 The calculation model of two-dimensional slope
3.2 实验设计
本文均匀设计表采用U27(2710),部分实验样本见表4。选取库岸边坡土性参数中黏聚力C、内摩擦角φ和重度γ的均值μ9 个水平,标准差σ3 个水平;边坡几何参数中坡角α和坡高H9 个水平;外部因素库水位h和水平地震加速度a9 个水平进行混合水平的均匀试验设计。
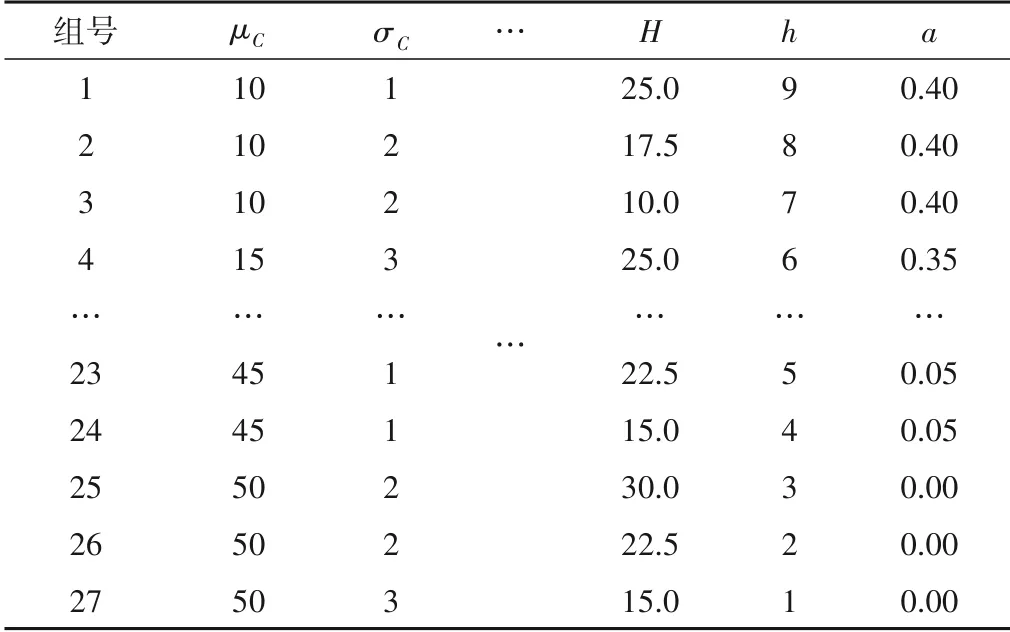
表4 实验样本Tab.4 Experimental samples
3.3 结果分析
在slide 程序中进行均质库岸边坡可靠度分析,求出27 组样本的计算结果即稳定性系数、失效概率和可靠度指标。基于MATLABR2018a 平台,在对表4试验样本中1~22 组与计算结果进行训练时,在PSO 算法初始参数中选定粒子群个数为50,网络隐含层数为20,加速常数c1=c2=2,初始惯性因子为0.9,终止条件为最大迭代次数为50,后将23~27 组进行测试。为分析PSO-RBF神经网络的预测效果,将其与本文算例边坡计算结果以及单纯的RBF 神经网络模型预测结果对比,网络预测结果见图4。
由图4可知,与相应的计算结果相比,在23~27 组预测结果中单纯的RBF 神经网络模型基本与其相一致,但个别结果有所欠佳,存在着较大偏差,如23、27 组的可靠度指标;23、25 和26组的失效概率P。相反在PSO-RBF 神经网络模型中则与计算结果十分接近,预测效果有很大提高。
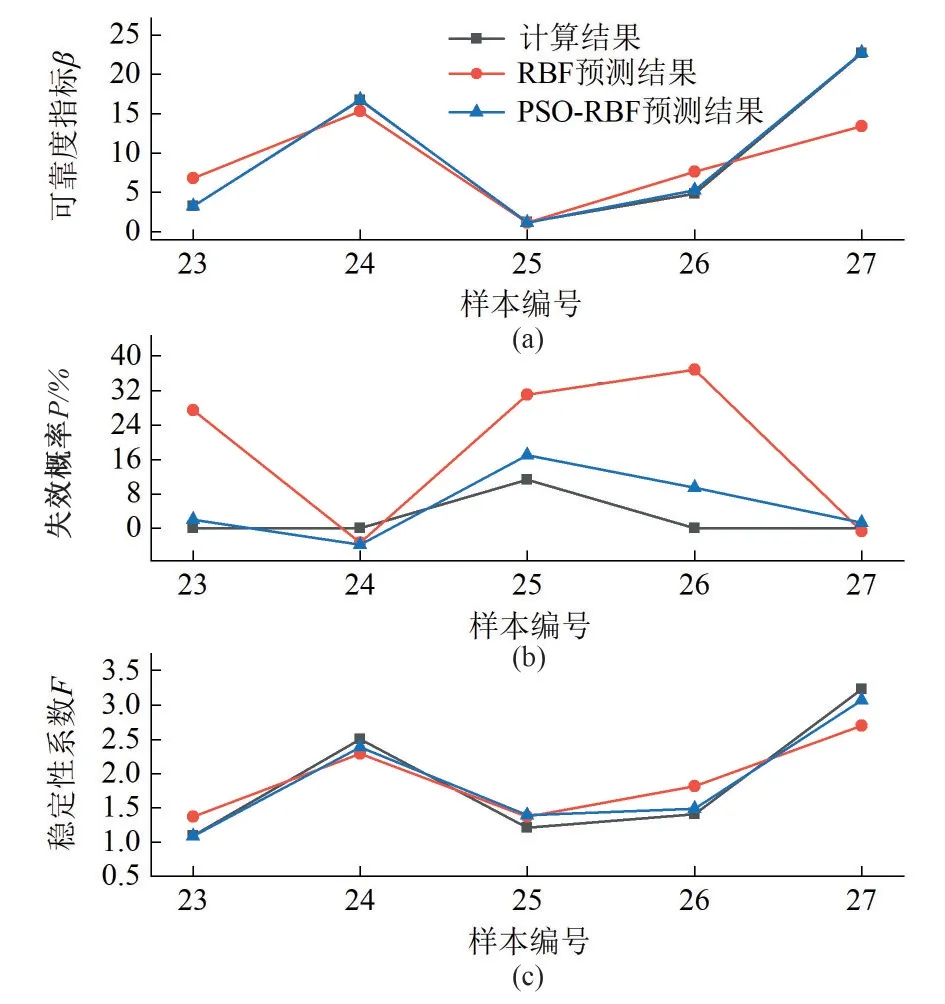
图4 计算结果与网络预测结果对比Fig.4 Compared with the calculated results and network prediction results
另外,由图4可以看出,对于算例中均质库岸边坡的计算结果的预测,PSO-RBF神经网络模型整体对计算结果的拟合效果相对会更好;此外在图4中(b)内可以看出对于失效概率P该网络预测结果也有一定偏差,但综合考虑可靠度指标β和稳定性系数F,该误差可接受,出现的原因是样本数量较少,网络训练不充分或是PSO 算法陷入局部最小点,为此可考虑增加实验样本数量或提高算法搜索能力。
为再进一步分析,通过网络预测结果可得平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)和均方误差(Mean Square Error,MSE),如表5所示,进一步可以得到在PSO-RBF神经网络中MAPE和MSE均小于前者,预测结果精度相较提高、离散性更低。由上述可知,PSO-RBF 神经网络对边坡计算结果的预测效果较好,且预测能力要明显RBF 神经网络,在预测精度方面有明显提高,实用性会更强。
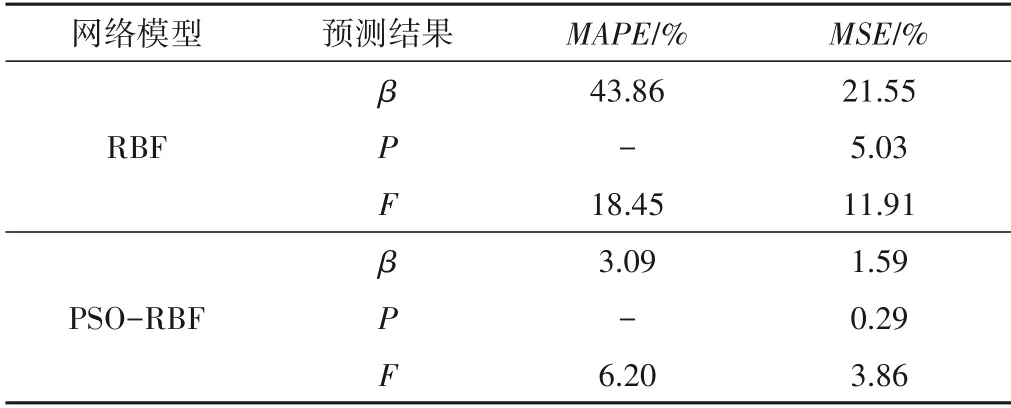
表5 网络预测结果误差对比Tab.5 Error comparison of network prediction results
另外从时间效率来看,虽然直接用slide程序计算库岸边坡的稳定性系数F较为快捷,但从建立模型、参数输入再到边坡的可靠度计算其中通常需要耗费较长时间。而PSO-RBF 神经网络预测模型一旦建成,预测耗时均不到1 min 即可完成,更可对多组边坡同时进行分析,显著提高了分析效率。
4 结 论
本文首先归纳库岸边坡土性参数以及几何参数与外部因素的分布范围,然后通过均匀试验设计建立并利用边坡实验样本及计算结果训练和检验PSO-RBF神经网络预测模型,完成了均质库岸边坡可靠度分析,通过预测结果得到以下结论。
(1)以边坡发生失稳破坏为依据,选择相应的影响因素及水平,建立了PSO-RBF 神经网络预测模型,并表明在本文因素考虑范围内进行的库岸边坡可靠度分析有较好的适用性。
(2)PSO算法原理简单,易于编程,收敛速度快,具有强大的全局搜索能力。通过与单纯的RBF 神经网络边坡预测模型对比,PSO-RBF 神经网络的平均绝对百分比误差在6.2%以下,均方误差最大为3.86%,可知选用PSO 优化能使RBF 神经网络预测精度能进一步提高,增强其实用性。
(3)通过PSO-RBF神经网络建立均质库岸边坡可靠度预测模型,省略了建模过程,减少了求解时间,可直接由边坡影响因素得到稳定性系数F、失效概率P和可靠指标β,显著提高了库岸边坡可靠度分析效率。
