钝角区腰线折角为零的月牙肋岔管研究
2022-01-24汪碧飞熊绍钧王启行李月伟
汪碧飞,熊绍钧,王启行,李月伟
(长江勘测规划设计研究有限责任公司,武汉 430010)
0 引 言
月牙肋岔管是由三梁式岔管不断演变、改进而来的一种岔管型式,因其结构受力好,管内水流平顺,水头损失小等优点,是目前国内外水利水电工程中应用较多的一种岔管型式[1-6]。月牙肋岔管一般由主管、主锥管、支锥管、支管及过渡管等组成,主锥管与支锥管的组合体称为基本锥。主锥管与支锥管之间存在夹角α0(图1 左),通常称为基本锥的钝角区腰线折角,《水利水电工程压力钢管设计规范》(SL∕T 281-2020)[7]规定钝角区腰线折角α0宜用10°~15°。国内许多文献[8-10]对岔管的体型进行了优化与设计研究,主要分析了公切球半径、分岔角及月牙肋的形状等因素对岔管的影响。文献[11]研究了钝角区腰线折角变化对岔管腰部、顶部等部位的应力影响的规律,得到了很多有意义的研究成果,但其没有分析钝角区腰线折角为零的方案。钝角区腰线折角为零是一种比较特殊的情况,钝角区腰线折角为零时(图1 右),主锥管与支锥管的腰线共线。拼装钝角区腰线折角为零的岔管时,调整主锥管与支锥管,使其腰线共线,相比存在折角的腰线,容易对齐,可适当降低加工难度与误差,利于岔管的制造与加工[12];此外,腰线折角为零的岔管其基本锥外形紧凑,轮廓尺寸较小,对岔管的布置、制造、运输及安装等较为有利。若腰线折角为零的岔管同时能满足受力要求,则腰线折角为零的岔管具有了工程应用价值。因此,本文采用有限元对钝角区腰线折角为零的岔管进行受力分析,研究其可行性,为今后的岔管设计提供依据与参考。
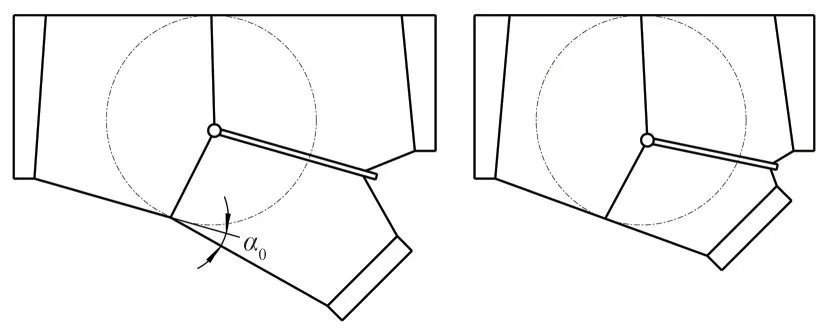
图1 月牙肋岔管简图Fig.1 Crescent-rib bifurcation
1 计算模型
1.1 基本资料
某地下电站引水管道采用一洞两机的布置形式,设置一个对称月牙肋岔管,主管直径3.0 m,两条支管直径2.2 m,分岔角70°。管道最大设计水头780 m,最大HD(H 为水头,D 为钢管内直径)值为2 340 m2。由于围岩条件较差,按明岔管设计。岔管管壁与月牙肋材料采用07MnMoVR 调质钢板,钢材弹性模量E = 206 GPa,泊松比v = 0.3,抗拉强度σb= 610 MPa,钢材允许应力按《水利水电工程压力钢管设计规范》(SL∕T 281-2020)[7]进行取值。
1.2 计算模型
为探讨腰线折角对岔管受力的影响,分别对钝角区腰线折角为9.9°、6.7°、3.2°及0°的4 种方案进行研究,对应地建立4 种计算模型。便于分析比较腰线折角对岔管受力的影响,4 种计算模型均保持岔管基本参数(如主管直径、支管直径、分叉角、公切球直径、岔管管壁厚度及肋板尺寸等)不变,仅调整钝角区腰线折角的大小。4种计算模型中基本锥(主锥管与支锥管)壁厚60 mm,主管壁厚46 mm,支管壁厚34 mm,公切球直径3.6 m,主管、支管与基本锥之间分别采用壁厚为54、48 mm 的过渡管连接,月牙肋板厚120 mm,月牙肋宽度900 mm,选取具有代表性的部位作为关键点进行对比分析,关键点位于过渡管与主锥管、过渡管与支锥管、主锥管与支锥管及岔管管壁与月牙肋的相交处,管壁上的关键点编号为A-L,月牙肋上的关键点编号为1-16,腰线折角为零的岔管体型及关键点分布见图2。
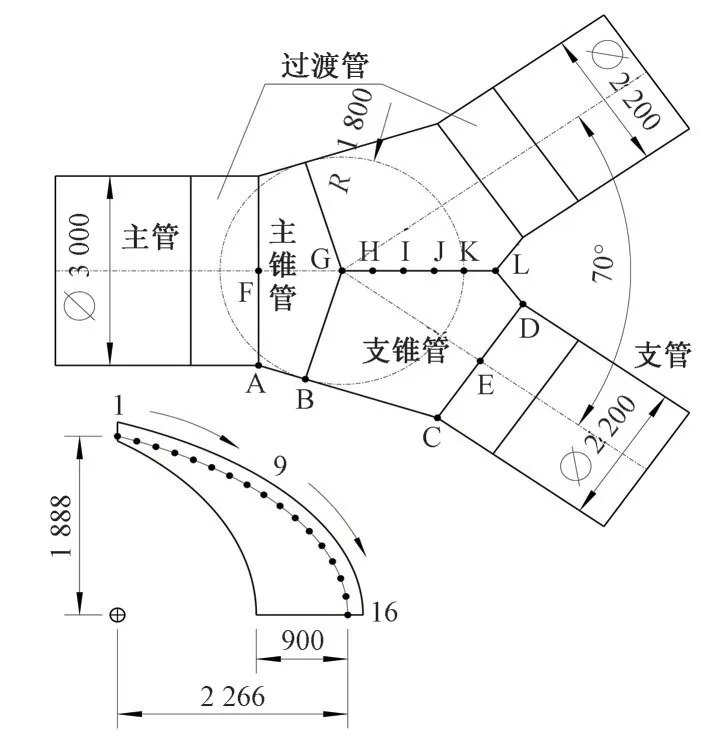
图2 腰线折角为0°的岔管体型及关键点分布图(单位:mm)Fig.2 Size and key points of bifurcation with waistline turning angle of 0°
采用ANSYS 计算程序进行有限元分析,钢岔管为线弹性,岔管管壁选用4 节点壳单元SHELL181 模拟,月牙肋较厚,选用8 节点实体单元SOLID185 模拟[13],主管与支管端部取固端约束,主、支管段轴线长度从公切球球心向上下游取公切球直径的1.5倍以上,岔管有限元模型见图3。
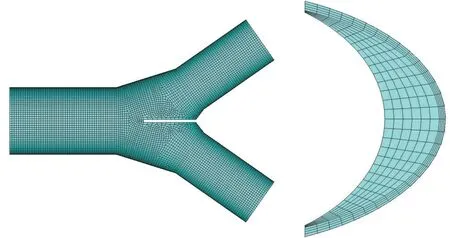
图3 腰线折角为0°的岔管有限元模型图Fig.3 Finite element model of bifurcation with waistline turning angle of 0°
2 计算结果
月牙肋岔管应力分布复杂,根据其受力特点,对岔管管壁的内表面、中面及外表面的Mises 应力进行了比较分析,月牙肋除了轴向应力较大外,在水压力的循环作用下,Z向应力可能会引起肋板的层状撕裂[14],因此对肋板的Z 向应力与Mises 应力进行了比较分析。
2.1 岔管管壁应力
腰线折角为9.9°与0°的管壁内表面Mises 应力云图分别见图4 与图5,腰线折角为9.9°、6.7°、3.2°及0°的管壁关键点的外表面、中面及内表面Mises 应力见图6,关键点A、B、C 及D 的Mises应力与腰线折角关系见图7~图10。由计算结果得知:①管壁内表面的应力相对较大,岔管壁厚一般由内表面应力控制,关键点A、B 及岔管顶部局部应力较大,其他部位的关键点应力水平相比较低。②不同腰线折角下,关键点A、B、C、D应力变化较大(图6),尤其A、B 两点变化明显,B 点应力随腰线折角的减小而降低,A 点应力则随腰线折角的减小而增加。③腰线折角为9.9°时,管壁最大Mises 应力为291.1 MPa,发生在B 点内表面,A 点内表面Mises 应力为278.3 MPa;腰线折角为0°时,管壁最大Mises 应力为300.2 MPa,发生在A 点内表面,B 点内表面Mises 应力为218.3 MPa;腰线折角0°与9.9°相比,A 点应力增加了7.9%,B 点应力减小了25.2%。④钝角区腰线折角的减少大大降低了岔管钝角区腰线折角处的应力水平(B 点周围,图5),同时,主锥管与过渡管的腰线折角处(A 点周围,图5)、支锥管与过渡管的腰线折角处(C点周围)的Mises应力增加了,主锥管与过渡管的腰线连接处的应力变为控制应力。⑤几种腰线折角的岔管承受内压能力基本一致,由于过渡管的壁厚小于岔管管壁厚度,可通过适当增加过渡管的壁厚降低主锥管与过渡管的腰线连接处的应力,进而提高岔管的抗内压的能力。
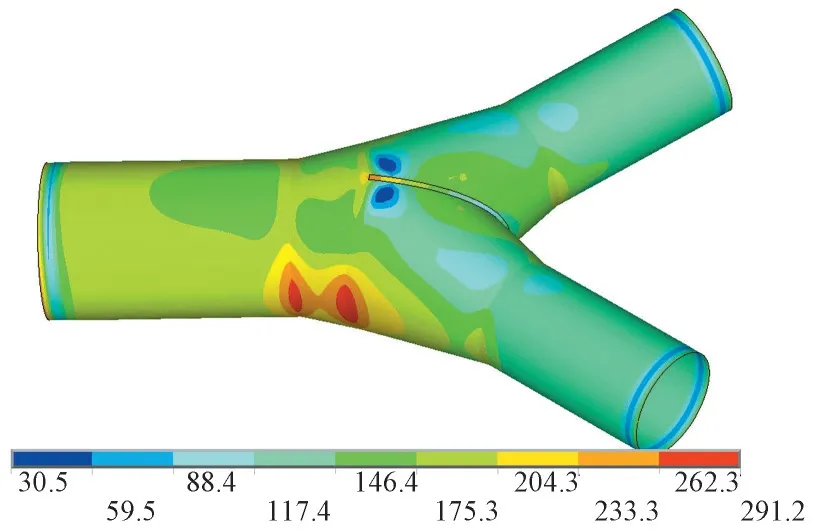
图4 腰线折角为9.9°的管壁Mises应力云图(单位:MPa)Fig.4 Mises stress of bifurcation with waistline turning angle of 9.9°

图5 腰线折角为0°的管壁Mises应力云图(单位:MPa)Fig.5 Mises stress of bifurcation with waistline turning angle of 0°
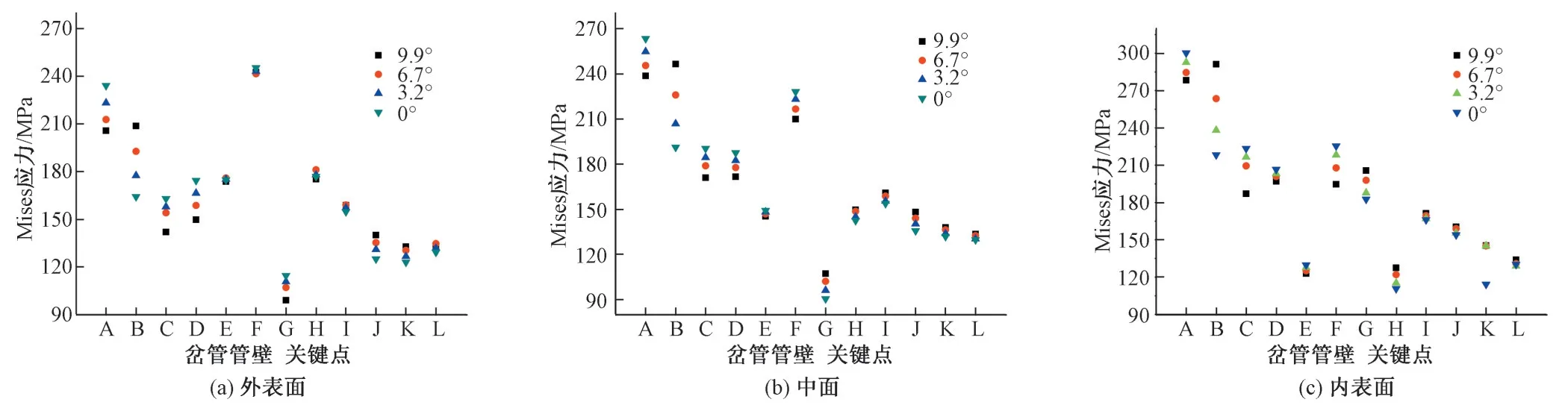
图6 岔管管壁关键点Mises应力Fig.6 Mises stress of key points of wall of bifurcation
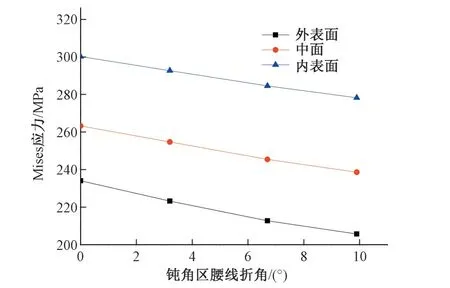
图7 岔管管壁关键点A的Mises应力与腰线折角关系曲线Fig.7 Relationship curve of Mises stress of Point A and waistline turning angle
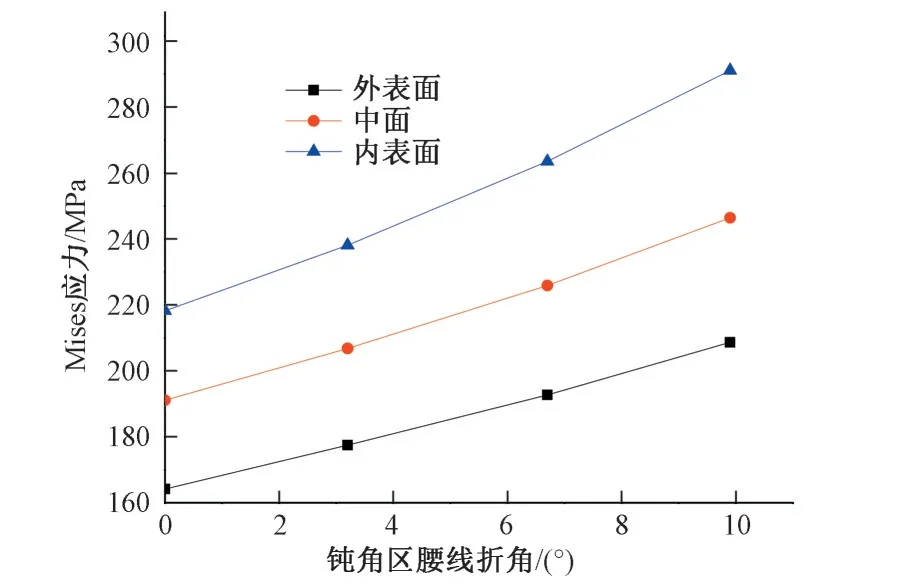
图8 岔管管壁关键点B的Mises应力与腰线折角关系曲线Fig.8 Relationship curve of Mises stress of Point B and waistline turning angle
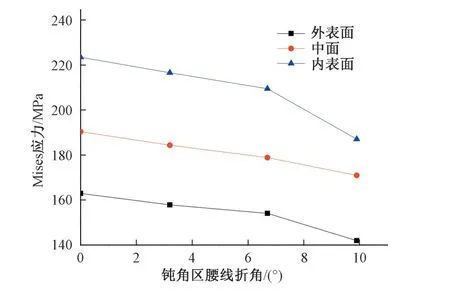
图9 岔管管壁关键点C的Mises应力与腰线折角关系曲线Fig.9 Relationship curve of Mises stress of Point C and waistline turning angle
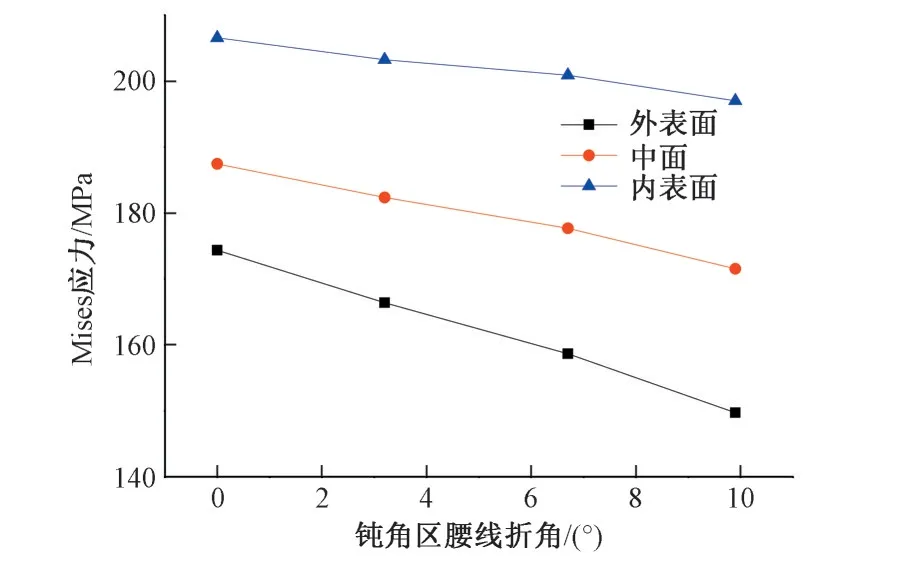
图10 岔管管壁关键点D的Mise应力与腰线折角关系曲线Fig.10 Relationship curve of Mises stress of Point D and waistline turning angle
3 结 论
2.2 月牙肋应力
腰线折角为0°的月牙肋Z 向(垂直于板面方向)应力与Mises 应力分别见图11 与图12,月牙肋关键点Mises 应力见图13。由计算结果得知:①月牙肋与左、右两侧支锥管相交处的Z向应力与Mises 应力较大,出现了应力集中现象,最大拉应力发生在月牙肋外表面的靠近上下两端处,腰线折角为0°时,最大拉应力为243.7 MPa(图11)。由于Z向应力很大,肋板Z向性能应符合《厚度方向性能钢板》(GB∕T 5313-2010)[15]相关规定。②月牙肋与左、右两侧支锥管相交处的Z 向应力沿板厚方向发生变化,外表面的Z 向应力大于内部的Z 向应力,其余部位Z 向应力较小,且沿厚度方向较为均匀。③腰线折角为9.9°与0°时,最大Mises 应力分别为271.1 MPa 与268.7 MPa,腰线折角对月牙肋受力影响很小,随着腰线折角的减小,应力有所降低(图13)。
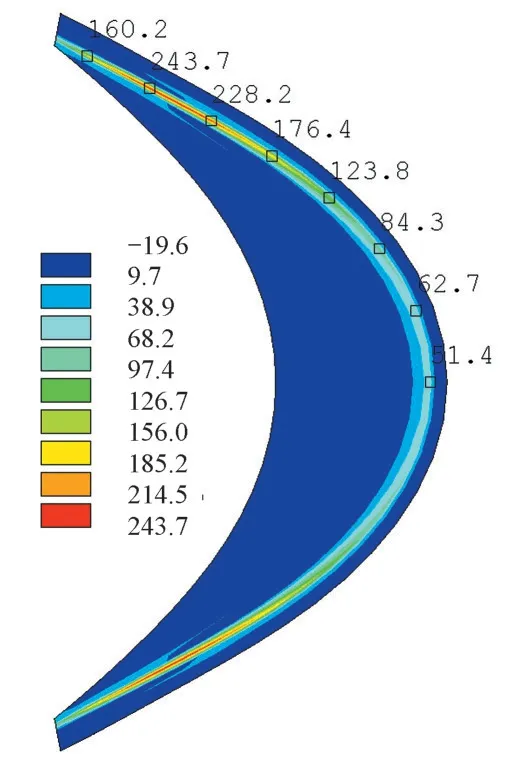
图11 腰线折角为0°的月牙肋Z向应力云图(单位:MPa)Fig.11 Stress of Z direction of crescent-rib with waistline turning angle of 0°
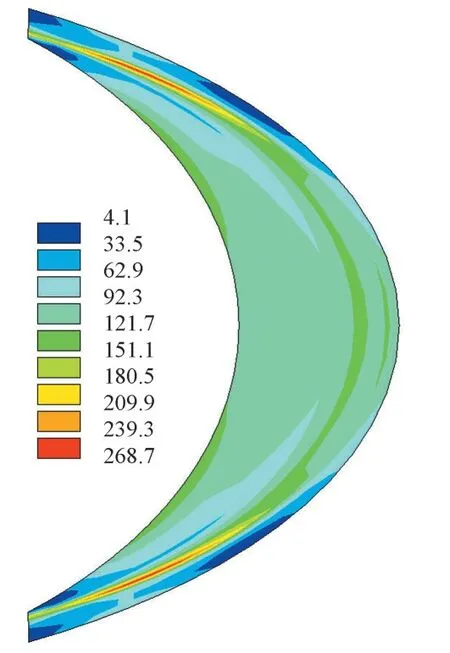
图12 腰线折角为0°的月牙肋Mises应力云图(单位:MPa)Fig.12 Mises stress of crescent-rib with waistline turning angle of 0°

图13 月牙肋关键点Mises应力与腰线折角关系曲线Fig.13 Relationship curve of external Mises stress of crescent-rib and waistline turning angle
(1)腰线折角为0°的岔管与其他几种折角的岔管管壁应力相当,前者最大应力发生在主锥管与过渡管的腰线连接处,后者发生在主锥管与支锥管连接处(钝角区腰线折角处),相同壁厚条件下,几种腰线折角的岔管能承受的内压值基本一致。由于过渡管的壁厚小于岔管基本锥管壁厚度,在保持基本锥壁厚不变的情况下,可通过适当增加过渡管的壁厚降低主锥管与过渡管的腰线连接处的应力,进而提高岔管承受内压的能力。
(2)腰线折角对月牙肋的应力影响较小,随着腰线折角的减小,应力有所降低。内水压力作用下,月牙肋与左、右两侧支锥管管壁相交处出现了较大的应力集中现象,Z向应力较大,同时,月牙肋与支锥管的焊缝收缩对肋板也会产生拉应力,因此必须保证月牙肋的Z向性能。
(3)当腰线折角为零时,锥管之间对齐、组装方便,降低了制造难度。
(4)腰线折角为零的Y 型对称岔管受力满足要求,可采用此设计方案,经计算分析,腰线折角为零的非对称Y 型岔管受力也具有上述特征。
(5)岔管腰线折角设置为零,则其他部位转折角增大,必然引起水流条件的变化。对于水流条件与水头损失要求高的岔管,还应进行水力学方面的论证。 □
