双参数层状地基中大直径单桩水平振动解析解与分析

辛 宇，崔春义，许成顺，梁志孟，王本龙，裴华富

（1.大连海事大学土木工程系，辽宁大连 116026；2.北京工业大学城市与工程安全减灾省部共建教育部重点实验室，北京 100124；3.大连理工大学海岸和近海工程国家重点实验室，辽宁大连 116024）

引言

桩-土动力相互作用作为岩土工程中的热点问题，一直受到学术界和工程界的关注［1-2］。近年来，随着交通基础设施及近海工程建设的大力发展，国内外学者对水平荷载作用下桩基动力响应问题进行了诸多层面的研究，并取得了丰富的研究成果［3-7］。

首先，因物理概念清晰和计算简单，Winkler地基模型在桩基水平动力分析中得到了广泛应用［8-10］。相比较而言，Pasternak双参数地基模型进一步考虑了地基土体剪切效应，更加符合实际［11-15］。因此，许多学者围绕双参数地基模型中桩基水平动力响应方面开展了系列研究工作。Dogan等［12］在均质双参数地基上将桩等效为欧拉-伯努利梁，利用拉格朗日方法推导得出桩基水平振动解析解，分析了Pasternak地基系数对桩基水平振动的影响规律。张望喜等［16］通过哈密顿原理和能量变分原理推导得出多层Pasternak 双参数地基中桩基受水平振动的解析解。王珏等［17-18］利用传递矩阵法推导得到Pasternak 双参数层状地基中单桩水平和回转振动阻抗解析解。

以上研究桩基模型均将桩体简化为Euler-Bernoulli 梁，只考虑了桩体弯曲变形，忽略了桩体剪切变形的影响。而对于大直径桩，采用能考虑桩身剪切变形的Timoshenko 梁模型则更为合理和必要［19］。基于此，早期Sun 等［20］、陈云敏等［21］考虑桩剪切变形影响，分别建立了单层和成层土中桩基水平振动控制方程，并推导出了对应解。进一步地，胡安峰等［22-24］基于Timoshenko 梁理论求解了复杂黏弹性地基中单桩水平动力响应，强调了忽略桩身剪切变形会引起较大误差。随后，章敏等［25］在Timoshenko梁模型基础上推导得出了桩顶水平频域响应解析解，研究了非饱和土中端承桩稳态水平振动特性。栾鲁宝等［26］将PCC 桩简化为Timoshenko 模型，进一步阐述了Timoshenko 模型与Euler-Bernoulli 模型计算桩顶阻抗时的差异性。

另一方面，上述研究均未考虑轴向荷载对桩基动力响应的影响，而在实际工程中桩基往往同时承受水平和轴向荷载作用［27-28］。围绕此点考虑，Catal［29-30］基于Winkler 模型，求解了在多向复杂荷载作用下的桩基振动方程。栾鲁宝等［31-32］考虑竖向荷载作用，分别求解了黏弹性地基中大直径管桩和饱和土中端承桩水平动力响应解析解，并进一步分析了竖向荷载对水平受荷桩动力响应的影响。

不难看出，在桩基水平振动已有研究中较少有同时考虑地基、桩基剪切变形和轴向荷载影响的相关研究。因此，本文将考虑轴向压力二阶效应的影响，将土体和桩基分别简化为Pasternak 双参数成层地基和Timoshenko 梁，建立大直径桩-成层土相互作用体系水平振动分析模型，进而结合桩土连续边界条件求解桩身位移、内力、转角的解析解，并与已有相关解析解进行退化对比验证其合理性。在此基础上，探讨桩身长径比、地基剪切层厚度、桩土模量比、桩身剪切变形系数及轴向荷载对桩基水平动力响应的影响规律。

1 力学模型描述与基本假定

基于Pasternak 地基模型的水平简谐激振作用下大直径单桩简化计算模型如图1所示。具体地，桩顶处施加水平简谐激振力Q0eiωt，其中Q0为激振力幅值，ω为激振圆频率，t为时间，N0为作用在桩顶的轴向压力。此外，第j层土的厚度、刚度系数、阻尼系数和地基剪切刚度分别为和；桩长、桩径分别为l和d；桩身微元体倾角、剪切角以及截面转角分别为α，β，φ，第j段桩截面弯矩为Mj。

图1 水平简谐激振作用下大直径单桩简化计算模型Fig.1 Simplified calculation model for a large diameter single pile under horizontal harmonic excitation

基本假定如下：

（1）桩身简化为圆形等截面、均质Timoshenko 梁；

（2）桩周土体沿桩身纵向划分为n层，每层土体简化为Pasternak 地基模型以描述桩-土相互作用；

（3）桩-土模型系统各部分均满足小变形条件，桩土界面为完全接触且无相对滑动；

（4）桩顶处仅发生水平位移，桩底处为固端约束。

2 定解问题力学模型的建立与求解

综合Timoshenko 梁和Pasternak 地基模型相关理论，得到第j（j为土层数，j=1，2，…，m，…，n）层段桩身单元的动力平衡方程如下：

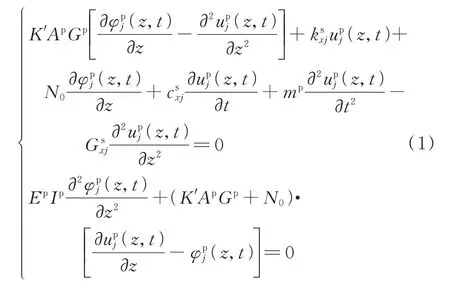
桩体水平位移和转角可表示为：

将式（5）代入式（1）可得：

显然，式（6）为四阶线性常系数微分方程，其对应的4个特征根为则可得其方程位移通解为：

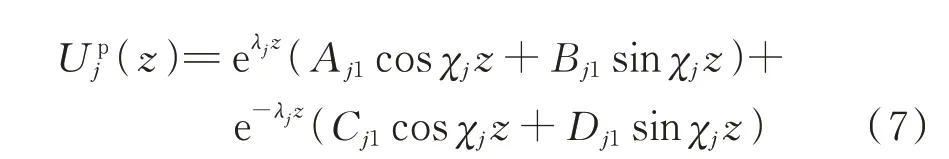
进一步地，由式（1）化简可得转角为：

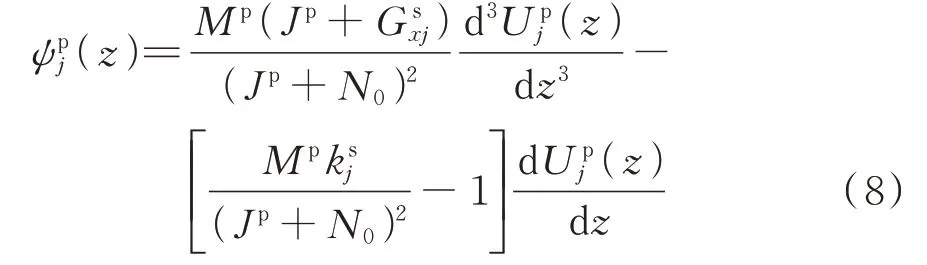
当桩体不发生剪切变形时（即Jp→∞），式（8）可退化为Bernoulli-Euler 理论解，即。

将式（7）代入式（8）可得转角通解为：

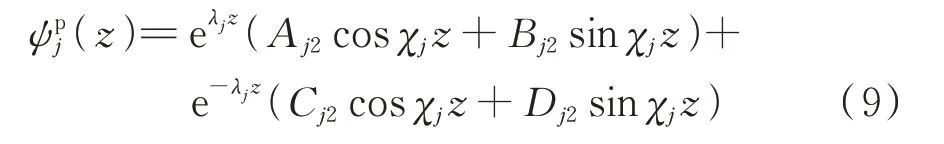
基于Timoshenko 梁理论，桩身弯矩、剪力与桩身水平位移相互关系为：

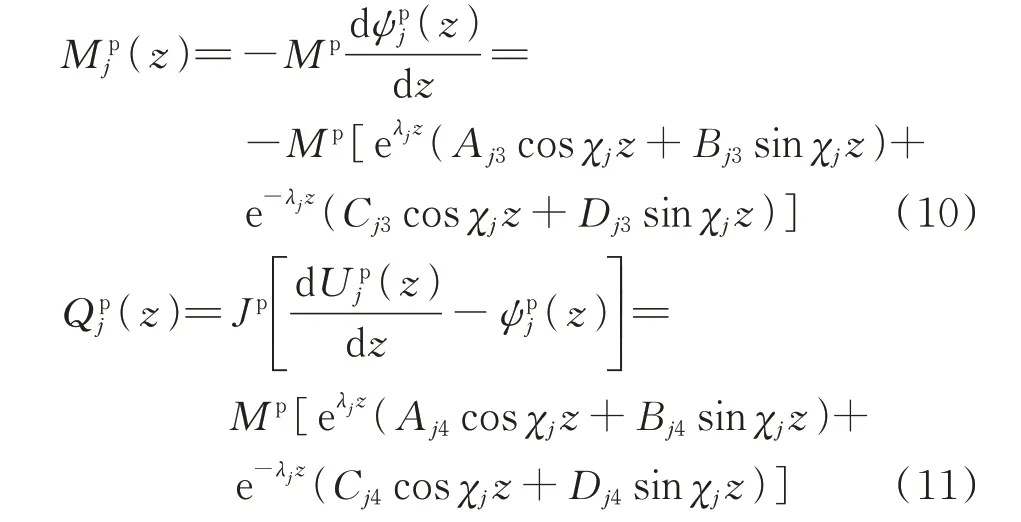
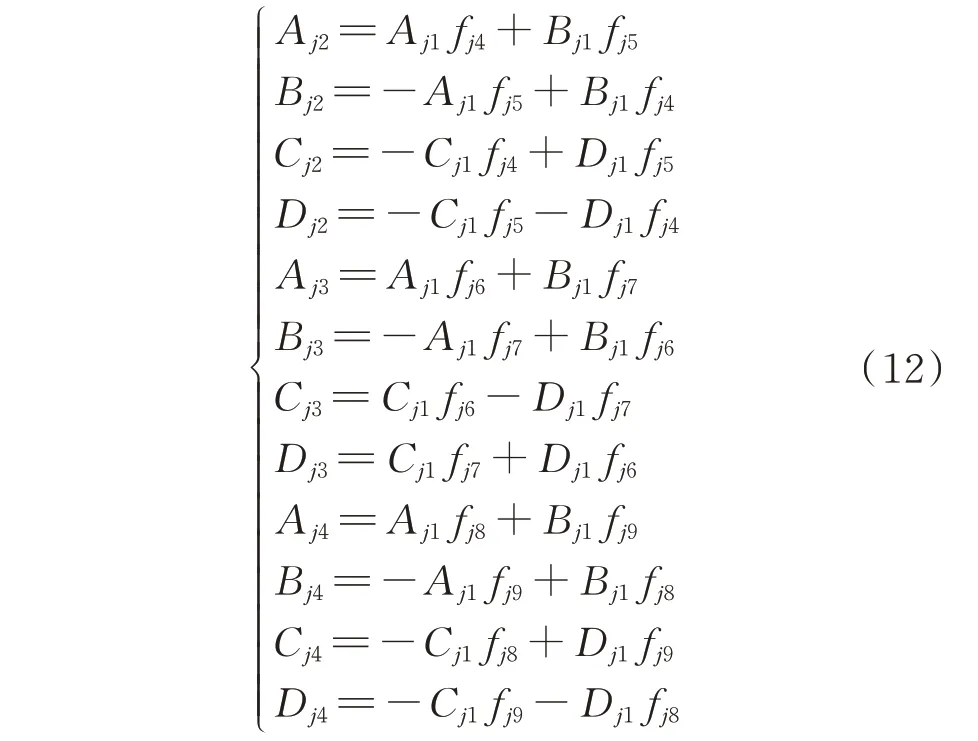
在第j段与第j+1 段桩身截面处，桩的水平位移、转角、弯矩及剪力连续，即：

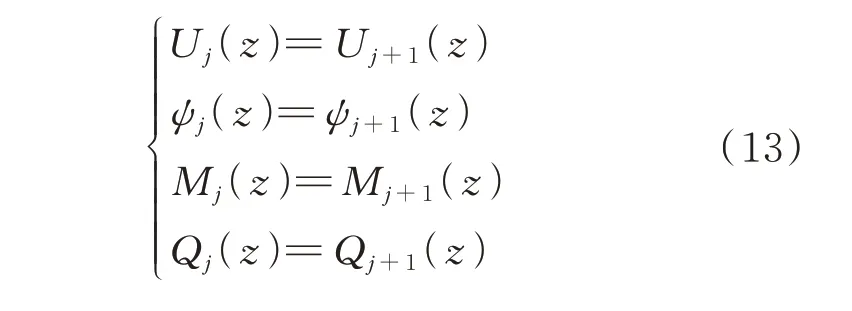
综合式（12）和（13）可得系数矩阵方程组如下：

由式（14）可得：

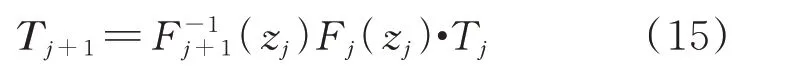
由递推关系可将第m段桩身对应系数矩阵Tm表示为：

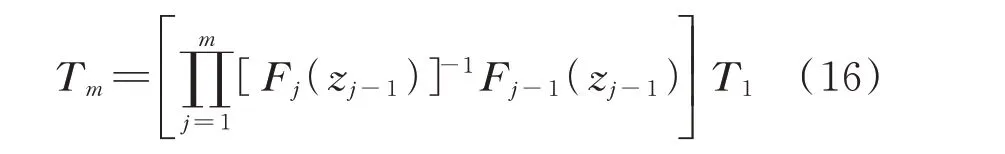
进一步考虑桩顶和桩底边界条件：

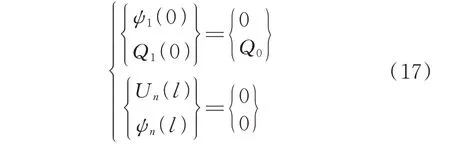
并将系数表达式（12）代入式（17），化简可得：

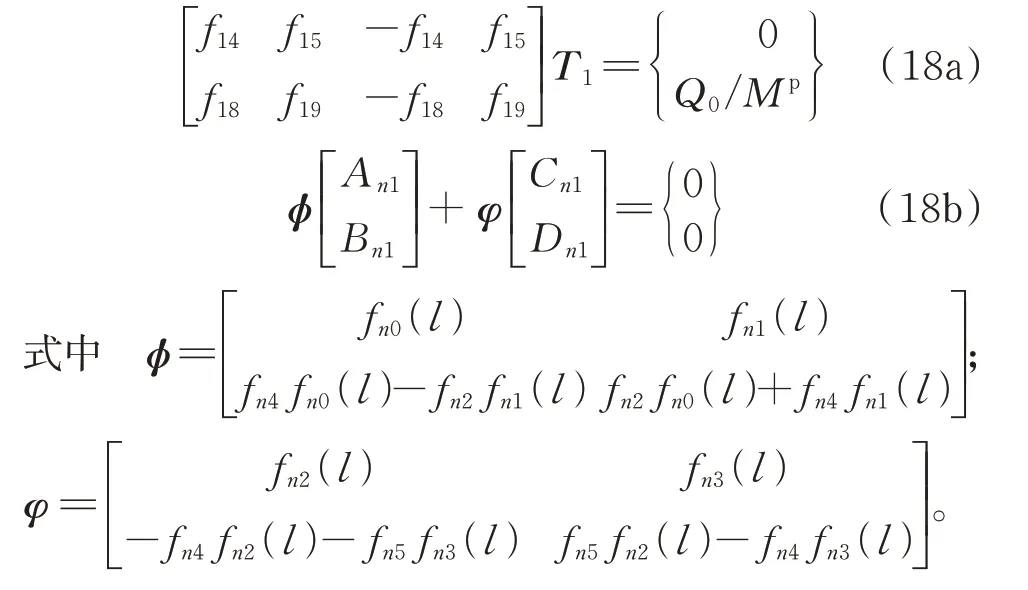
联立式（16）～（18）则可求出T1，再根据递推公式（16），最终可求出m段桩身对应系数矩阵Tm，进而可求得桩身各段水平位移；根据桩身水平位移表达式，利用桩身弯矩、剪力与桩身水平位移之间的关系，可求出桩身弯矩、剪力。

为便于后续分析，定义如下位移、弯矩、剪力无量纲包络值参量如下：

式中umax(z)，mmax(z)，qmax(z)分别为每个动力循环中桩基水平振动位移、弯矩和剪力最大值。

便于更清晰地说明上述推导过程，图2 给出了对应求解流程图。

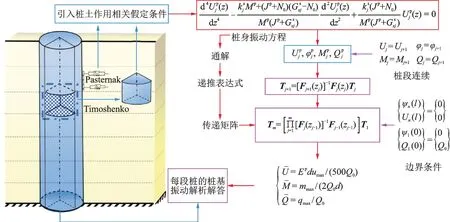
图2 单桩求解流程示意图Fig.2 Schematic diagram of single pile solution process

3 算例分析

关于大直径单桩的界定及相关参数取值参照已有相关研究［22-24，31-32，35］。如无特殊说明，算例中计算参数选取如下：土层参数n=3、第j层土阻尼系数、泊 松 比、密 度103kg/m3、弹性模量、桩土弹模比、桩长l=8 m、桩径d=1 m、桩体密度ρp=2.5×103kg/m3、桩体剪力形状系数K′=3/4、无量纲频率a0=0.5、外荷载幅值Q0=100 kN。

特别需要强调的是，为方便说明问题，后续分析中位移、弯矩、剪力振动响应均采用前述定义的无量纲包络值参量描述。

3.1 解析解的合理性验证

为了验证本文所推导的大直径单桩水平动力响应解析解的合理性，不考虑轴向荷载的影响（N0→0），首先将桩体由Timoshenko 梁退化为Euler-Bernoulli 梁（Jp→∞），本文退化解与文献［18］解的对比情况如图3所示。同时，将土层Pasternak 模型退化至模型，本文退化解与文献［24］解的对比情况如图4所示。由图可见，本文所推导大直径单桩水平振动响应解析解的退化解分别与已有解结果吻合。

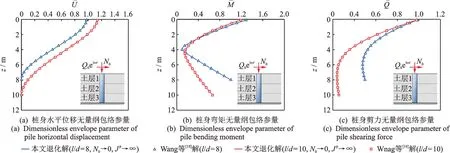
图3 本文退化解（N0 →0，Jp →∞）与Wang 等［18］已有解分布对比情况Fig.3 Comparison of present solution（N0 →0，Jp →∞）with Wang，et al in Ref.［18］

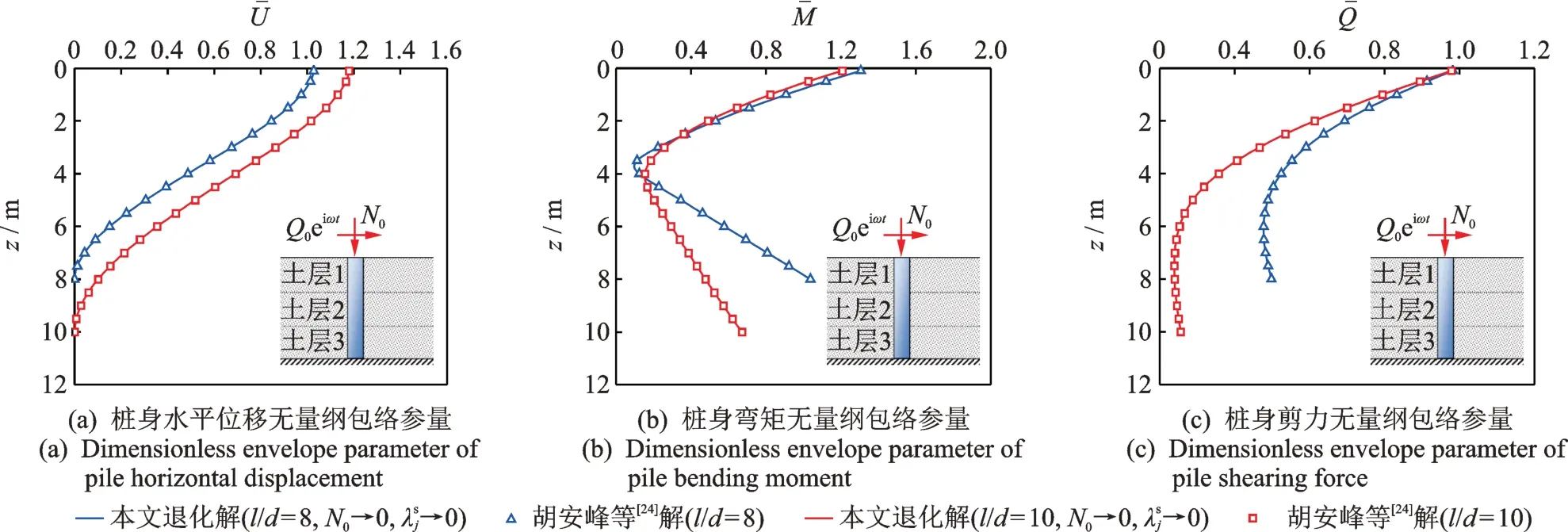
图4 本文退化解

3.2 桩基参数化对比分析

为进一步分析桩基和层状地基剪切变形对桩体水平振动响应的影响，分别将本文计算模型中桩体由 Timoshenko 梁 退 化 为 Euler-Bernoulli 梁（Jp→∞），桩周土Pasternak 地基退化为Winkler 地基，即将本文P-T（Pasternak-Timoshenko）模型退化至W-E（Winkler-Euler）模型。由文献［10］

Fig.4 Comparison of present solutionwith Hu An-feng，et al in Ref.［24］可知，当桩长径比（即桩长与桩直径的比值）l/d＜8时，桩身剪切效应的影响不可忽视。具体地，算例中分别选取桩体长径比l/d=3，6，桩土弹模比为Es=Ep/5000。

图5所示为上述两种模型计算所得桩身水平位移、弯矩及剪力无量纲包络参量分布对比情况。由图5（a）可见，P-T 模型和W-E 模型计算所得桩身水平位移无量纲包络参量的最大值均出现于桩顶，且水平位移无量纲包络参量随土层深度增加呈减小趋势。特别地，地基浅层范围内（本文z＜1 m），采用两种模型计算所得桩身水平位移无量纲包络参量差异较为明显，且此种差异随土层加深而渐至可以忽略。图5（b）中桩顶弯矩无量纲包络参量均大于桩端，桩身无量纲包络参量在半桩长处出现反转拐点，且此后随土层深度的增加，两种模型计算所得桩身无量纲弯矩包络参量差异变大。此外，由图5（c）可以看出，桩身剪力无量纲包络参量均随土层深度的增加而减小，且采用两种模型计算所得桩身剪力无量纲包络参量差值随土层深度的增加呈现出先增大后减小的趋势。综上不难看出，由于考虑了桩周土和桩身剪切变形的影响，本文所采用P-T 模型计算桩身内力结果均比W-E 模型对应结果偏小。

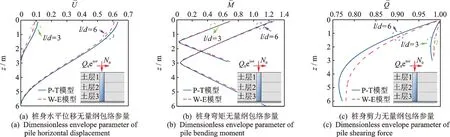
图5 P-T 模型和W-E 模型计算所得桩身无量纲包络参量分布对比情况Fig.5 Comparison of the distribution of dimensionless envelope parameters of the pile body calculated by P-T model and W-E model

图6所示为不同桩身长径比条件下的桩身水平位移、弯矩、剪力无量纲包络参量分布对比情况。由图6 可见，不同桩长径比条件下的桩身水平位移无量纲包络参量，均随桩身长径比的增加而增大；长径比越小，后半桩长段无量纲弯矩包络参量增幅越大，并随长径比的增大而减小；桩身无量纲剪力包络参量随桩长径比的增加而减小。综上所述，当桩身长径比较小时，桩身长径比变化对桩身无量纲水平位移、弯矩和剪力包络参量均影响显著，且此种变化影响随桩径比增大而逐渐变小，并趋于稳定。

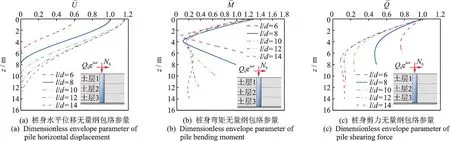
图6 不同桩长径比条件下桩身水平位移、弯矩及剪力无量纲包络参量分布对比情况Fig.6 The comparison of pile dimensionless envelope parameters of horizontal displacement，bending moment and shearing force under different pile slenderness

为进一步分析桩土弹模比对桩基水平位移、弯矩、剪力无量纲包络参量的影响规律，分析工况具体如表1所示。其中，Case1～Case3 为表层土Ep/Es1的变化工况，Case4～Case6 为夹层土Ep/Es2的变化工况。

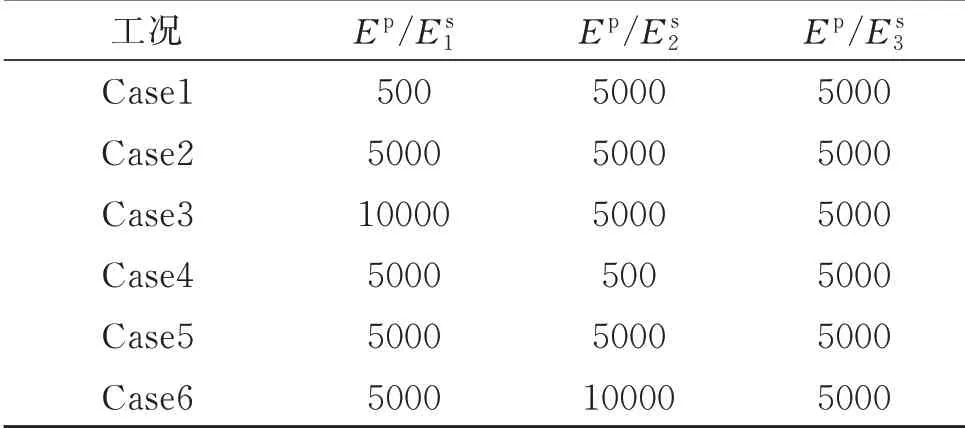
表1 桩-土弹模比工况Tab.1 Distribution of pile-soil modulus ratio

如图7所示为桩土弹模比变化对桩基水平位移无量纲包络参量的影响情况。从图中可以看出，在同一深度条件下，随表层土、夹层土对应桩土弹模比的增加，桩顶水平位移无量纲包络参量幅值变大。图8 和9所示分别为桩土弹模比变化对桩基弯矩、剪力无量纲包络参量的影响情况。由图可见，在同一深度条件下，随着表层土、夹层土对应桩土弹模比的增加，桩身弯矩和剪力无量纲包络参量均变大。相比较而言，表层土桩土弹模比的变化对桩顶水平位移、桩身弯矩和剪力无量纲包络参量的影响更为显著。

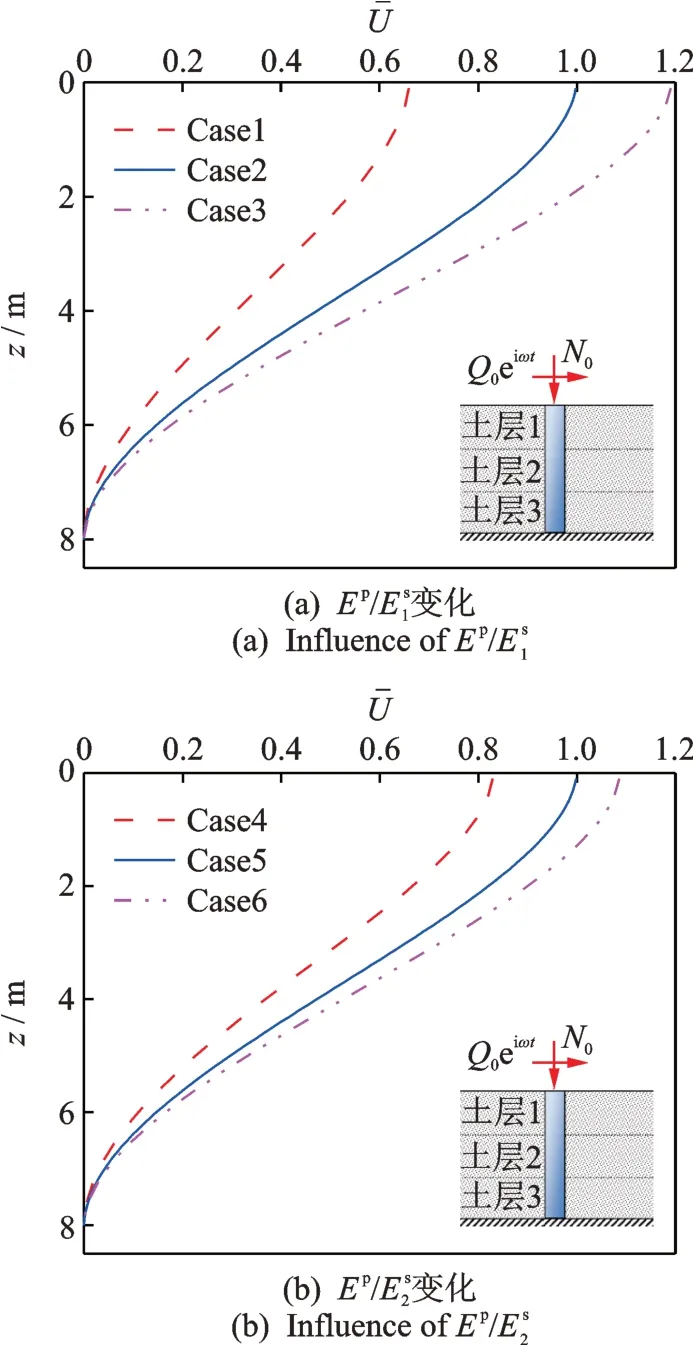
图7 桩土弹模比变化对桩身水平位移无量纲包络参量的影响Fig.7 Influence of pile-soil elastic modulus ratio on the dimensionless envelope parameters of pile horizontal displacement

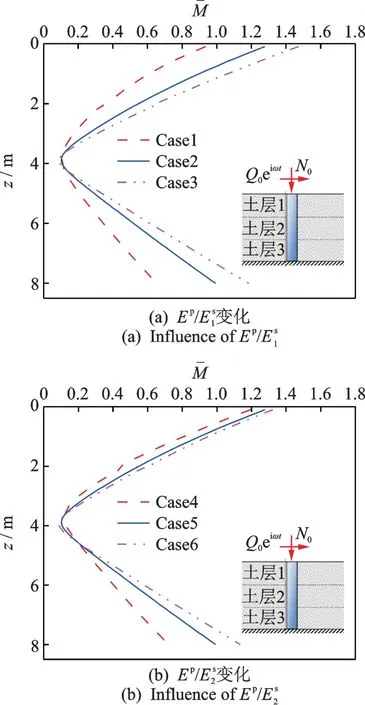
图8 桩土弹模比变化对桩身弯矩无量纲包络参量的影响Fig.8 Influence of pile-soil elastic modulus ratio on the dimensionless envelope parameters of pile bending moment

为了方便说明问题，引入与桩体截面形状有关的剪力形状系数K′（见公式（1））。具体地，当截面形状为圆形时，K′一般取为3/4；当横截面为方形时，K′一般取为2/3；当横截面为环形截面时，K′=，其中R为外圆半径，r为内圆半径［36］。

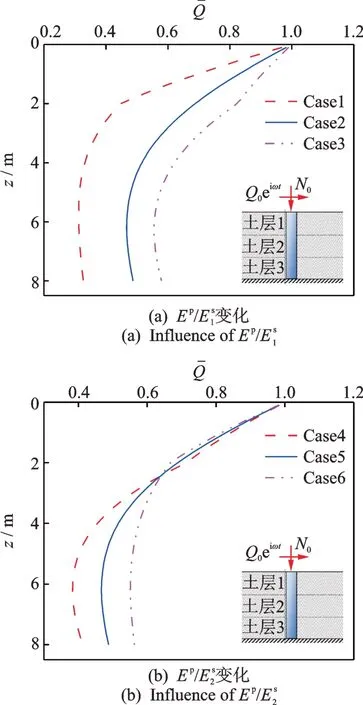
图9 桩土弹模比变化对桩身剪力无量纲包络参量的影响Fig.9 Influence of pile-soil elastic modulus ratio on the dimensionless envelope parameters of pile shearing force

图10所示为桩截面变化对桩身水平位移、弯矩及剪力无量纲包络参量分布的影响情况。其中，同时将本文解中桩体由Timoshenko 梁退化为Euler-Bernoulli 梁（Jp→∞），即由P-T 模型退化为P-E 模型进行对比分析。由图可见，在相同截面条件下，P-T 模型对应的桩身水平位移无量纲包络参量大于P-E 模型计算结果；P-T 模型对应的桩身内力无量纲包络参量小于P-E模型计算结果。特别地，在环形截面条件下，P-T 模型对应的桩身水平位移和内力无量纲包络参量与P-E 模型计算结果差异最为显著。而对于圆形截面而言，此种差异很小甚至可以忽略。这也就是说，对于环形截面的大直径管桩而言，在进行桩基水平振动特性分析时考虑桩体剪切变形影响十分必要。

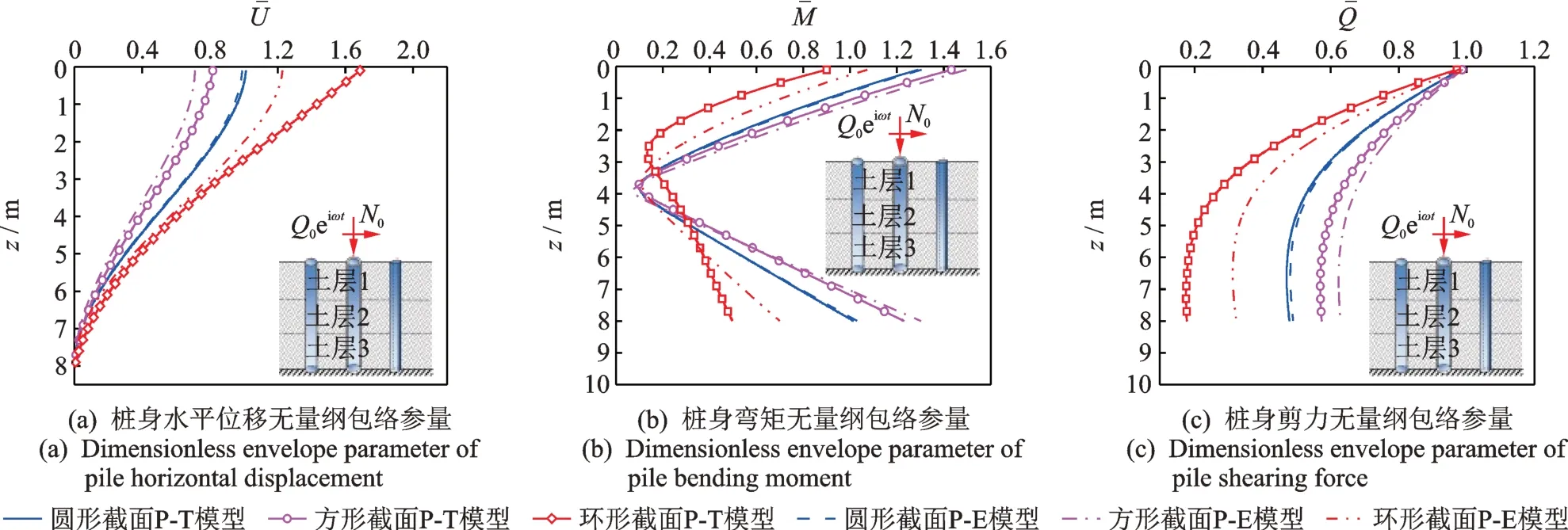
图10 桩截面对桩身水平位移、弯矩及剪力无量纲包络参量分布的影响Fig.10 The comparison of pile dimensionless envelope parameters of horizontal displacement，bending moment and shearing force under different pile sections

考虑轴向力N0作用时，定义，并将δ（δ=0，1，2，4）作为考虑轴向二阶效应的特征参数［37］。轴向作用特征参数变化对桩身水平位移、弯矩及剪力无量纲包络参量分布的影响如图11所示。因桩顶受轴力和水平力耦合作用可产生P-Δ效应。由图可见，随着轴向作用特征参数的增加，水平位移无量纲包络参量显著增大。不同地，仅下半段桩身弯矩和桩端一定区域以外的剪力无量纲参量随轴向作用特征参数的增加而增大。因此，在实际工程中桩顶轴向荷载对桩基水平振动特性的影响不可忽视。

图11 轴向荷载对桩身位移、弯矩及剪力无量纲包络参量分布的影响Fig.11 Influence of axial loads on the dimensionless envelope parameters of pile shearing force

4 结论

本文土体采用Pasternak 地基模型，将桩基简化为Timoshenko 梁，建立了大直径桩-成层土相互作用体系水平振动分析简化分析模型，采用微分变换方法对方程解耦，并结合桩土连续边界条件求解相关解答。在此基础上，探讨了桩身长径比、地基剪切层厚度、桩土模量比、桩身剪切变形系数及轴向荷载对桩基水平振动特性的影响规律。计算分析结果表明：

（1）由于考虑了桩周土和桩身剪切变形的影响，采用P-T 模型计算桩身内力无量纲包络参量结果均比W-E 模型偏小。不同地，采用P-T 模型计算桩身水平位移无量纲包络参量结果比W-E 模型偏大，且此种差异随土层加深而渐至可以忽略。

（2）随着内部区域土体软（硬）化程度的加大，扭转阻抗曲线振幅明显增大（减小），但内部区域土体软（硬）化程度对扭转阻抗曲线共振频率的影响可以忽略。

（3）在相同截面条件下，P-T 模型对应的桩身水平位移无量纲包络参量大于P-E 模型计算结果；PT 模型对应的桩身内力无量纲包络参量小于P-E 模型计算结果。特别地，在环形截面条件下，P-T 模型对应的桩身水平位移和内力无量纲包络参量与P-E模型计算结果差异最为显著。

（4）随着轴向作用特征参数δ的增加，水平位移无量纲包络参量显著增大。不同地，仅下半段桩身弯矩和桩端一定区域以外的剪力无量纲参量随轴向作用特征参数δ的增加而增大。

（5）本文所采用解析模型和推导所得对应解析解答，能综合考虑轴向压力二阶效应、桩周土和桩身剪切变形的影响，并针对求解相关解答进行了退化对比验证，可为大直径桩基工程相关水平向振动分析和设计提供参考。