某航空发动机整机系统非线性振动特性分析
2022-07-26林荣洲孙传宗侯升亮陈予恕
林荣洲,侯 磊,,孙传宗,杨 洋,侯升亮,陈予恕
(1.哈尔滨工业大学航天学院,黑龙江哈尔滨 150001;2.西南交通大学力学与航空航天学院应用力学与结构安全四川省重点实验室,四川成都 611756;3.沈阳工业大学机械工程学院,辽宁沈阳 110870)
引言
航空发动机作为飞机的动力来源,它的性能直接决定了飞机的性能、可靠性以及成本。但由于航空发动机工作环境复杂,除了受到发动机运转的不平衡激励以外,还受到气动激励、热场等的影响,导致航空发动机的振动问题一直是航空领域的重要研究课题[1]。
航空发动机是一种旋转机械,对于转子-轴承系统的研究,各个国家的学者已经做出了比较多的研究。Nelson 等[2]就开始运用有限元法对转子-支承系统进行建模,并计算了该系统的临界转速、不平衡响应,验证了有限元法研究转子-轴承系统的有效性。随着非线性振动的兴起,转子转速的提高,转子的非线性振动问题也开始受到关注。Ertas 等[3]对一含有平方非线性的2 自由度转子系统进行了分析,发现了1∶2 内共振、振动突跳等现象,并给出了该系统发生内共振的条件。Young 等[4]运用HB/AFT 方法对含分段非线性的多自由度转子系统进行了求解,验证了该方法的准确性。Tiwari 等[5]对支承于球轴承上的刚性转子进行了分析,考虑了球轴承的Hertz 接触非线性,发现了轴承间隙以及变刚度会使转子系统发生倍周期分岔,最后通过实验验证了这一结论。Diken[6]对含平方非线性的Jeffcott 转子进行了分析,发现了非线性可能导致转子发生亚谐共振。Jing 等[7]建立了考虑油膜力作用的转子-轴承系统的动力学模型,分析了油膜力对该系统的分岔特性的影响,发现在转速下降时,会发生油膜涡动和油膜振荡交换的现象。Hou 等[8-9]研究了机动飞行条件下转子-球轴承系统的非线性振动响应,发现在机动飞行条件下系统产生了亚谐共振,并且发现在特定转速时会发生周期1 与周期2 运动交换、周期2 运动与概周期运动交换的现象。
对于转子系统的动力学特性研究,还包括轴承故障[10-12]、碰摩[13-17]等问题,也取得了许多成果。但现代航空发动机为了满足高速、高推重比的要求,多采用双转子结构。航空发动机的双转子结构较为复杂,双转子靠中介轴承连接,并且双转子通过轴承与机匣连接,最终机匣再与飞行器连接。而对于这样一个复杂结构,从整机振动的角度去考虑是十分必要的。在航空发动机整机振动方面,国外有一些成果,Bonello 等[18]对含有挤压油膜阻尼器的航空发动机整机系统进行动力学建模,引入了导纳谐波平衡法(RHBM)对整机系统进行分析,将该方法与传统的脉冲响应法对比,发现导纳谐波平衡法对整机系统的非线性动力学分析是很有效的。国内对整机振动也有丰富的研究,洪杰等[19]、于平超等[20]针对高推重比涡扇发动机的质点动载荷振动响应及优化设计问题,建立了转子系统支点动载荷力学模型,研究了不平衡力以及轮盘惯性载荷等因素对支点动载荷的影响,结果表明通过优化高压涡轮后轴颈结构能有效减小中介支点动载荷大小。张大义等[21]、Yu 等[22]将有限元法与振型筛选法结合,提出了适用于工程应用的临界转速求解方法,并验证了其准确性。王俨剀,廖明夫等[23-25]通过对3 种典型航空发动机中介轴承各30 台份的试车数据统计,得到使中介轴承免受“同步冲击”的原则;同时提出将发动机的健康状态量化,将模糊综合评价方法应用于发动机健康状态等级的评估;最后通过对两组发动机故障模拟实验器振动数据的等级评价结果对比,验证了该方法的有效性。陈果[26-29]考虑了航空发动机整机系统转子与轴承和机匣的耦合效应,挤压油膜阻尼器等多种因素,建立了转子-球轴承-机匣耦合系统的动力学模型,运用Newmark-β 法和翟方法相结合进行求解,得到了整机系统的临界转速、不平衡响应,着重分析了挤压油膜阻尼器对整机系统的振动特性的影响,最终用实验验证了模型的准确性。周海仑等[30]以双转子航空发动机为研究对象,建立了航空发动机双转子-滚动轴承-机匣耦合动力学模型,用龙格-库塔法进行求解,结果表明,碰摩故障下,整机系统可能从概周期演变为混沌。孙传宗等[31]以机匣-双转子试验台为研究对象,用ANSYS 建立了高精度的实体有限元模型,运用Craig-Bampton 模态综合法实现了子模型维度缩减,最后通过实验验证了该方法的准确性。
可以看出对于航空发动机转子部分非线性振动特性的研究已经很丰富了,但航空发动机的信号监测的测点一般都位于机匣上,转子部分的各类振动行为在机匣上是何种表现形式的问题却鲜有研究。因此,本文以某型号航空发动机整机振动试验台为研究对象,运用有限单元法建立简化的整机系统动力学模型,并考虑中介轴承的Hertz 接触非线性弹性恢复力,结合Newmark-β 法与Newton-Raphson 法进行数值求解,着重研究中介轴承间隙对整机系统非线性振动响应的影响规律,并分析高低压转子上的各类非线性振动现象在机匣上不同位置测点的表现形式,进而讨论航空发动机机匣上的测点安排。
1 整机系统动力学建模
1.1 基本假设
某型号航空发动机双转子结构图如图1所示,该发动机共有6 个支点,其中1#,2#,6#为低压转子支点,3#和5#为高压转子支点,4#为连接高低压转子的中介轴承。

图1 航空发动机双转子结构图Fig.1 Structure diagram of aeroengine dual-rotor
参照文献[32-33]中的结构简化方法,将高低压转子的转盘通过质量集中和惯性等效进行合并简化,同时将机匣简化为等截面圆柱筒,进而建立了航空发动机整机系统的简化模型,如图2所示。图中坐标原点o在低压转子压气机顶端处,坐标轴oz与高低压转轴的中心线重合。模型中低压压气机部分等效为2 个轮盘L1 和L2,1 个低压涡轮部分等效为1 个轮盘L3,高压压气机部分等效为1 个轮盘H1,高压涡轮部分等效为1 个轮盘H2。在轮盘与支承处划分节点,将低压转子划分为8 个节点,高压转子划分为7 个节点,内涵道机匣划分为5 个节点,外涵道机匣划分为6 个节点,其中节点Ⅰ,Ⅱ,Ⅲ依次为机匣的前测点、中测点以及后测点。
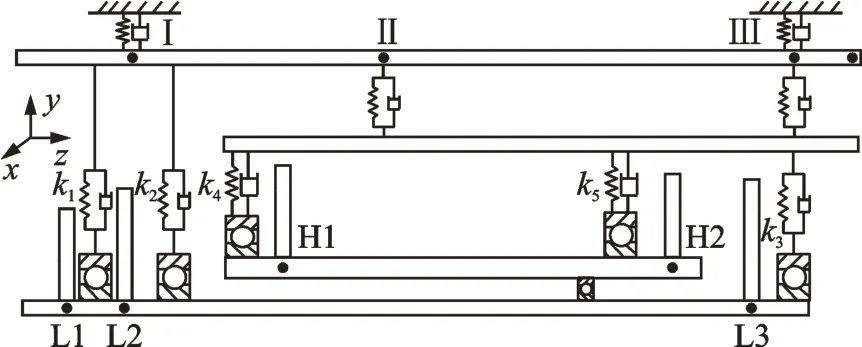
图2 航空发动机整机系统结构简图Fig.2 Structure diagram of overall aeroengine system
建模时考虑的假设如下:
(1)高、低压压气机和高、低压涡轮的轮盘都考虑为具有回转效应的刚性圆盘。
(2)转轴简化为等截面的空心梁,不考虑转轴的扭转与轴向运动的影响,主要考虑转子的横向弯曲运动。
(3)支承刚度视为弹性支承和轴承支承的组合刚度,而中介轴承则考虑滚子的Hertz 接触非线性。
(4)假设在工作转速内机匣的截面不变形,保持为圆形截面,但机匣轴线有弯曲模态,将机匣处理为不旋转的等截面空心梁。
运用有限元法对整机系统进行动力学建模[34],首先将整机系统分为双转子系统与机匣,分别建立了双转子与机匣的动力学方程后,再将其组装为整机系统。
对于低压转子有L个节点,高压转子有H个节点,机匣有C个节点,总共有N个节点的航空发动机整机系统,可以设其位移向量为:
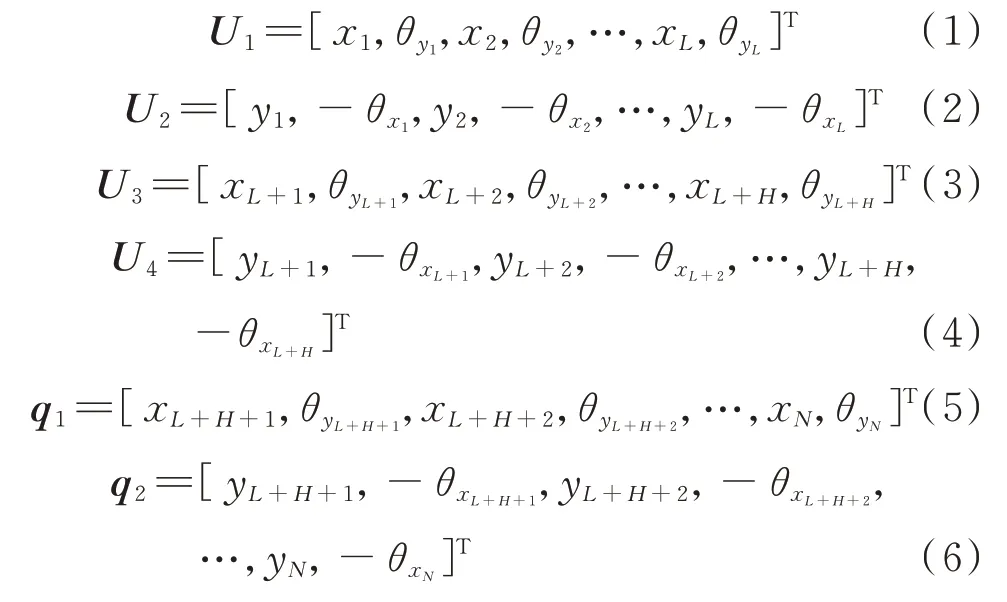
式中U1,U2分别表示低压转子的广义位移向量;U3,U4分别表示高压转子的广义位移向量;q1,q2分别表示机匣轴心的广义位移向量。
1.2 刚性圆盘、弹性轴段和弹性支承的建模
通过列写各单元的运动方程,可以得出各个单元的质量矩阵、惯性矩阵和刚度矩阵。其中,刚性圆盘的质量矩阵Md和惯性矩阵J可以表示为:
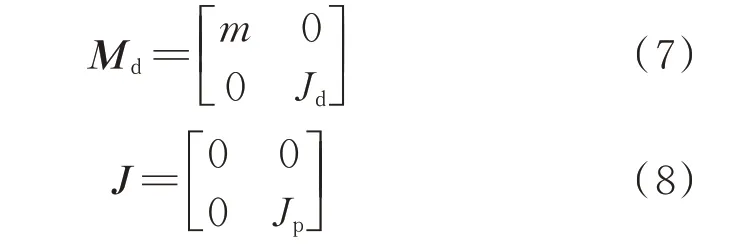
式中m为圆盘质量;Jd,Jp分别为圆盘的直径转动惯量和极转动惯量。
弹性轴段的质量矩阵Mz、惯性矩阵Jz和刚度矩阵Kz分别表示为:


式中μ为轴段密度,l为轴段长度,A为轴段截面面积,E为杨氏模量,Iz为轴段惯性矩。m1=312+588φ+280φ2,m2=(44+77φ+35φ2)l,m3=108+252φ+140φ2,m4=-(26+63φ+35φ2)l,m5=(8+14φ+7φ2)l2,m6=-(6+14φ+7φ2)l2,m7=36,m8=(3-15φ)l,m9=(4+5φ+10φ2)l2,m10=(-1+5φ+5φ2)l2,,κ为剪切修正系数。
1.3 弹性支承及中介轴承的建模
弹性支承的刚度矩阵可以表示为:

式中kbx,kby别为轴承座x,y两个方向的刚度,并且一般情况下kbx=kby。
中介轴承位于高低压转子之间,轴承内圈与低压转子相连,轴承外圈与高压转子相连,则中介轴承恢复力在x,y方向的投影可以表示为:

式中Cb为接触刚度系数,H(·)为Heaviside 函数。δei,θei为第i个滚动体与滚道接触时的变形及第i个滚动体的位置,分别表示为:

式中 Δx,Δy分别表示内圈中心以及外圈中心在x,y方向上的相对位移;δ为中介轴承的间隙。Nb为滚动体个数;Ωc为保持架转速。
1.4 整机系统动力学方程的组装
将机匣考虑为不会旋转的梁进行建模,则它具有和弹性轴段相同的质量矩阵和刚度矩阵,但不具有惯性矩阵。通过综合各个单元的运动方程,以节点位移相容的原则,对刚度矩阵、惯性矩阵和质量矩阵进行拼合,最终可以得到系统的运动方程。
独立的低压转子、高压转子、机匣的无阻尼自由振动方程依次如下:
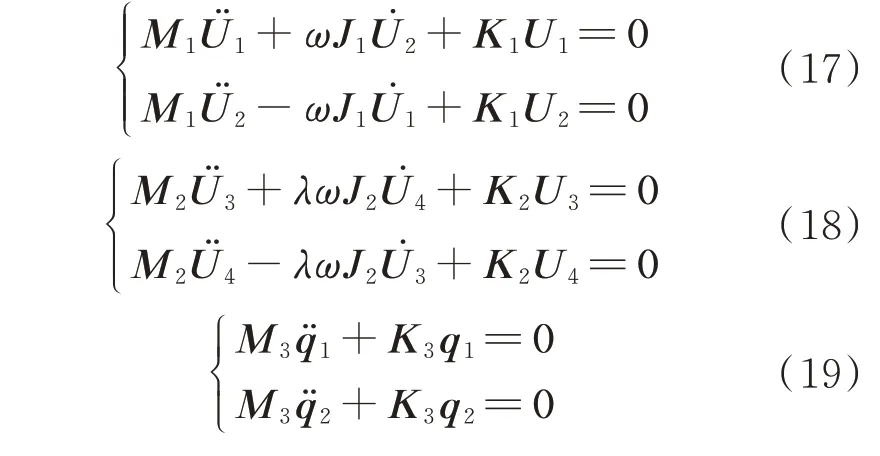
式中M,J,K分别代表拼合的质量矩阵、惯性矩阵、刚度矩阵;下标1,2,3 依次代表的是低压转子、高压转子、机匣;λ代表高低压转子转速比,本文中取高低压转速比为1.2;ω代表低压转子自转角速度。

式中Qbx,Qby包含了中介轴承引起的非线性恢复力Fbx,Fby以及施加于转盘上的不平衡激励力依次表示施加于第i个转盘上不平衡激励在x,y方向上的投影;mi,ωi,δri依次表示第i个转盘的质量、转盘对应转子的转速以及转盘的偏心距。本文施加于转盘上的偏心距如下表1所示。表中转盘编号与图2 相对应,L1 和L2 为低压压气机盘,L3 为低压涡轮盘,H1 为高压压气机盘,H2 为高压涡轮盘。而偏心距为圆盘质心相对于圆盘几何中心的偏移量。

表1 转子偏心距Tab.1 Eccentricity of rotor
再以类似方式将式(18)与(19)组合,此时转子与机匣刚度矩阵非对角线上应含有耦合刚度。则可以得到整机系统的无阻尼动力学方程:
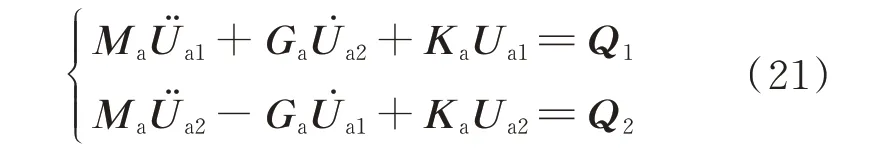
式中Ma,Ga,Ka分别为整机系统的质量矩阵、陀螺矩阵以及刚度矩阵,Ua为整机系统广义位移,Q为整机系统广义力,其中下标1表示x方向,下标2表示y方向。
再考虑整机受比例阻尼Ca=αMa+βKa作用,其中α,β为比例阻尼系数,可以通过下式确定:
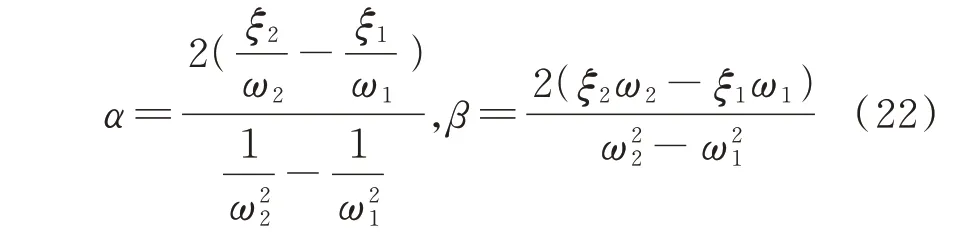
式中ξ1,ξ2为模态阻尼比;ω1,ω2为整机系统的第1阶和第2 阶临界转速。
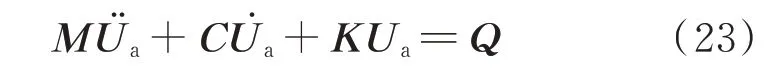
为了了解整机系统的固有特性,不妨先参照文献[35]近似计算中介轴承径向刚度如下式所示:
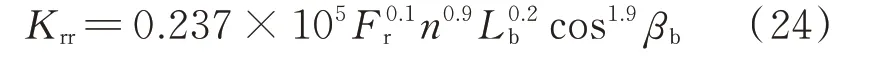
式中d为滚珠直径,Lb为滚子有效长度,n为滚子数目,βb为接触角,Fr为径向外力,本文中为轴承所承受的轴段和盘的重力。
利用式(24)进而将中介轴承等效线性化。然后求解式(23)的广义特征值问题,可以得到整机系统线性化条件下的临界转速与振型,其中前两阶临界转速依次为772,1649.7 rad/s,对应的前两阶振型如图3所示。可以看出第1 阶振型为高压涡轮盘的振动,低压转子由于中介轴承的作用也会有一些振动。第2 阶振型为低压压气机盘的振动。
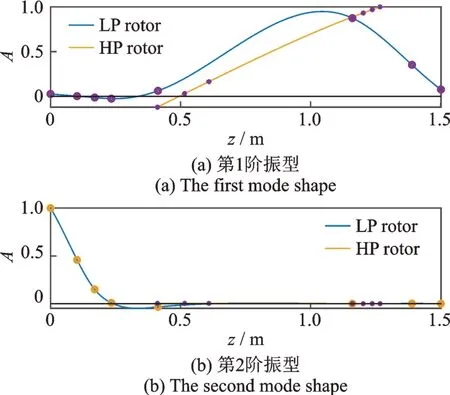
图3 整机系统前2 阶振型Fig.3 The first 2 mode shapes of overall aeroengine system
同时为了验证模型的准确性,通过商业有限元软件建立了高精度的有限元模型,同样计算其临界转速与振型,其前2 阶临界转速对比如表2所示,可以看出简化后临界转速误差不超过10%;而商业有限元软件振型如图4所示,简化前后振型不变,验证了模型的准确性。

表2 整机系统临界转速对比Tab.2 Comparison of critical speed of overall aeroengine system

图4 高精度有限元模型计算的整机系统前2 阶振型Fig.4 The first 2 mode shapes of overall aeroengine system using high accuracy finite element model
2 中介轴承间隙对高低压转子非线性振动特性的影响
采用Newmark-β 与Newton-Raphson 结合的方法[36-37]进行数值求解,可以得到整机系统各个节点的位移响应。由于航空发动机为双转子结构,因而存在双频不平衡激励,其振动响应中存在至少两种频率成分。为了更清晰地反映振动的强度,本文采用振动信号能量的有效值[38]来表示常规幅频曲线中的振幅:
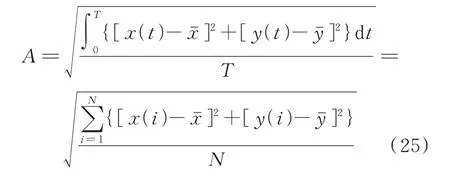
式中x(t),y(t)为系统节点对应方向的位移响应;T为高、低压转子不平衡激励周期的公倍数,不妨称其为公共周期;xˉ,yˉ为公共周期T内的位移相应响应平均值;N为公共周期T离散的总点数,可以画出以有效值A为幅值的幅频响应图。
中介轴承间隙是中介轴承的关键参数,它的大小会很明显地影响整机系统的动力学特性。图5给出了中介轴承不同间隙下低压转子压气机1盘的幅频响应曲线,其中ω为低压转子的转速,图中实线是升速曲线,虚线是降速曲线。由于中介轴承非线性,因此该条件下的第1阶临界转速与线性化条件下计算的临界转速并不完全相等。由图可知,在高低压转速比λ为1.2,整机系统在第1 阶临界转速下(760 rad/s)时,低压压气机1盘并未出现共振峰,由图3(a)可知,整机系统第1阶临界转速对应的振型是高压转子涡轮盘的振动,且由于低压压气机1盘是一个悬臂结构,它的幅频响应没有明显的共振峰出现,只有幅值随着不平衡响应的增大而增大。并且增大中介轴承间隙对低压压气机1盘的振动特性没有显著影响。
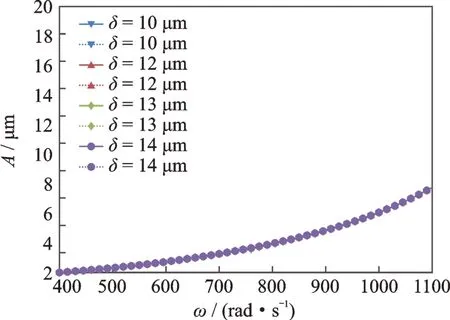
图5 低压压气机1 盘幅频响应曲线(实线为升速曲线,虚线为降速曲线)Fig.5 Amplitude-frequency response of low pressure compressor disk L1(full lines are run up,dotted lines are slow down)
低压转子压气机2 盘和低压转子涡轮的幅频响应分别如图6 和7所示。可以看出,在第1 阶临界转速下有两个共振峰,第1 个共振峰对应的低压转子转速633.3 rad/s,该共振峰是由高压转子不平衡激励引起的,第2 个共振峰对应的转速是760 rad/s,是低压转子不平衡激励引起的。由于高压转子转速大于低压转子的转速,因此高压转子先通过第1 阶临界转速,低压转子后通过。
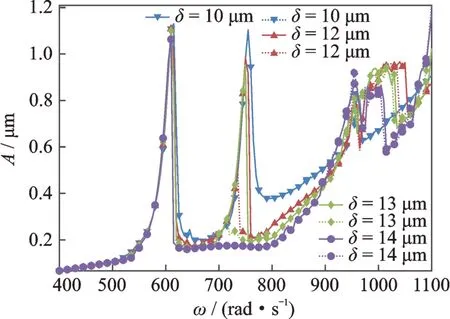
图6 低压压气机2 盘幅频响应曲线(实线为升速曲线,虚线为降速曲线)Fig.6 Amplitude-frequency response of low pressure compressor disk L2(full lines are run up,dotted lines are slow down)
高压转子压气机与涡轮的幅频响应分别如图8和9所示。高压转子的情况与低压转子的情况相类似,但高压转子涡轮的振幅大于低压转子涡轮的振幅,高压压气机的振幅也大于低压压气机的振幅,这是因为此时的振型是高压转子涡轮的振动,而通过中介轴承的传递,低压转子涡轮也有较大的振动,高压压气机与低压压气机则振动较小。
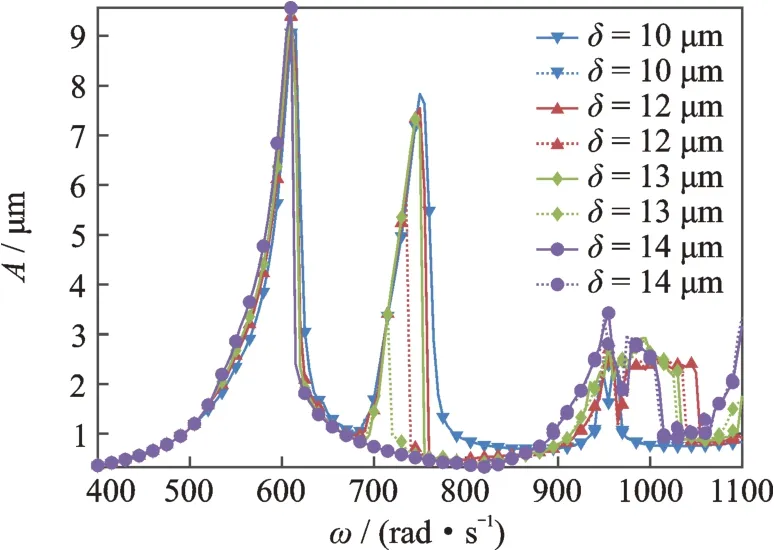
图8 高压压气机幅频响应曲线(实线为升速曲线,虚线为降速曲线)Fig.8 Amplitude-frequency response of high pressure compressor disk H1(full lines are run up,dotted lines are slow down)
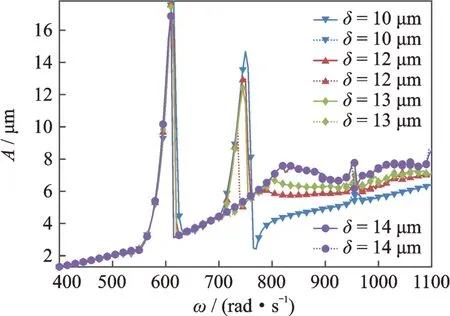
图7 低压涡轮幅频响应曲线(实线为升速曲线,虚线为降速曲线)Fig.7 Amplitude-frequency response of low pressure turbine disk L3(full lines are run up,dotted lines are slow down)
同时注意到,对于除了低压压气机1 盘以外的部位,如图6~9所示,当中介轴承间隙δ=12 μm 时,第2 个共振峰均出现了振动突跳现象,但第1 个共振峰则并未出现这一现象。同时在系统升速过程中跳跃点与降速过程中跳跃点之间形成了双稳态区间,当增大间隙时,两个共振峰对应的临界转速都有略微的减小,两个共振峰对应的幅值也略有减小,其中第2 个共振峰的减小幅度大于第1 个共振峰。对于双稳态区间而言,增大中介轴承间隙,第1 个共振峰还是没有出现双稳态现象,而第2 个共振峰的双稳态区间开始增大。
当继续增大中介轴承间隙,达到δ=14 μm 时,幅频响应图中第2 个共振峰“消失”。为了继续探究这一现象,分别给出间隙δ=10,14 μm 的情况下高压转子涡轮与低压转子涡轮处的时间历程图、频谱图以及轴心轨迹图,如图10 和11所示。可以看出,在δ=10 μm 时,高、低压转子涡轮的频谱中既有高压转子不平衡激励频率Ω2=λω,也有低压转子不平衡激励频率Ω1=ω,并且低压转子不平衡激励频率的幅值较大,表明该共振峰主要是由低压转子不平衡激励激起的。从轴心轨迹图可以看出此时的轴心轨迹为高低压转子的耦合,是一些圆的交错叠加。

图10 低压涡轮在ω=760 rad/s,δ=10 μm 下的时间历程图、轴心轨迹图与频谱图Fig.10 Time history,orbit of shaft and frequency spectrum of low pressure turbine at ω=760 rad/s,δ=10 μm

图11 高压涡轮在ω=760 rad/s,δ=10 μm 下的时间历程图、轴心轨迹图与频谱图Fig.11 Time history,orbit of shaft and frequency spectrum of high pressure turbine at ω=760 rad/s,δ=10 μm
如图12 和13所示,在δ=14 μm 时,低压转子涡轮处的频谱中的低压转子不平衡激励频率Ω1为主要频率成分,高压转子不平衡激励频率Ω2只有很少的贡献。而高压转子涡轮处的频谱则情况相反,此时高压转子不平衡激励频率Ω2为主要频率成分,而Ω1的贡献很小,说明此时高低压转子各自运动,几乎没有耦合作用。由图3(a)可知,系统第1 阶振型为高压转子的振动,因而低压转子的不平衡激励并不能有效传递到高压转子,因此低压转子激起的共振峰“消失”。从轴心轨迹可以看出此时低压转子与高压转子的轴心轨迹都为比较规则的单圆环的叠加。

图12 低压涡轮在ω=760 rad/s,δ=14 μm 下的时间历程图、轴心轨迹图与频谱图Fig.12 Time history,orbit of shaft and frequency spectrum of low pressure turbine at ω=760 rad/s,δ=14 μm
因此,当中介轴承间隙增大到一定程度(δ=14 μm)时,会发生滚动体与滚道不接触的现象,导致高低压转子的耦合程度降低甚至于“脱离”,在达到相应的临界转速时,低压转子的不平衡激励并不能有效地传导到高压转子使之发生共振。
此外,如图9所示,当中介轴承间隙δ=10 μm时,高压涡轮的幅频响应在低压转子转速为950 rad/s 处出现了一个共振峰。为了分析这一现象,分别给出了δ=1,5 和10 μm 时,低压转子转速ω=950 rad/s,高低压转速比λ=1.2 情况下,高低压转子涡轮处的时间历程图、频谱图以及轴心轨迹图,如图14~16所示,其中(a)~(c)依次为低压转子涡轮的时间历程、频谱图和轴心轨迹图,(d)~(f)依次为高压转子涡轮的时间历程、频谱图和轴心轨迹图。

图9 高压涡轮幅频响应曲线(实线为升速曲线,虚线为降速曲线)Fig.9 Amplitude-frequency response of high pressure turbine disk H2(full lines are run up,dotted lines are slow down)
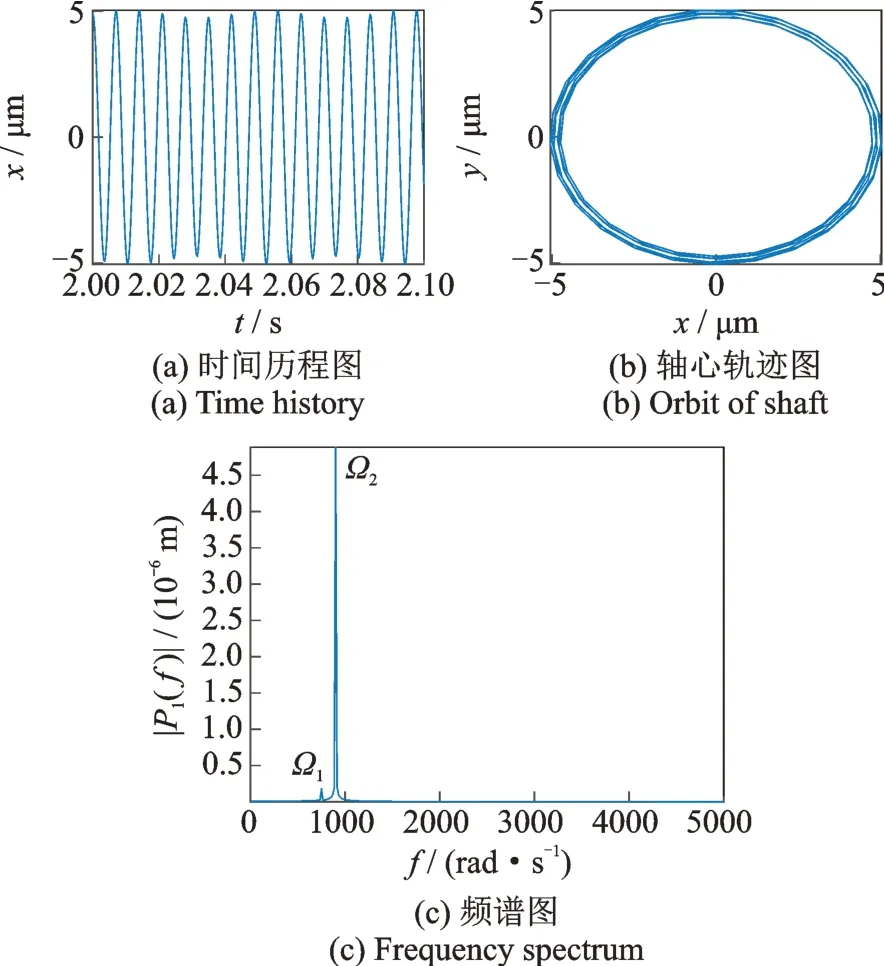
图13 高压涡轮在ω=760 rad/s,δ=14 μm 下的时间历程图、轴心轨迹图与频谱图Fig.13 Time history,orbit of shaft and frequency spectrum of low pressure turbine at ω=760 rad/s,δ=14 μm
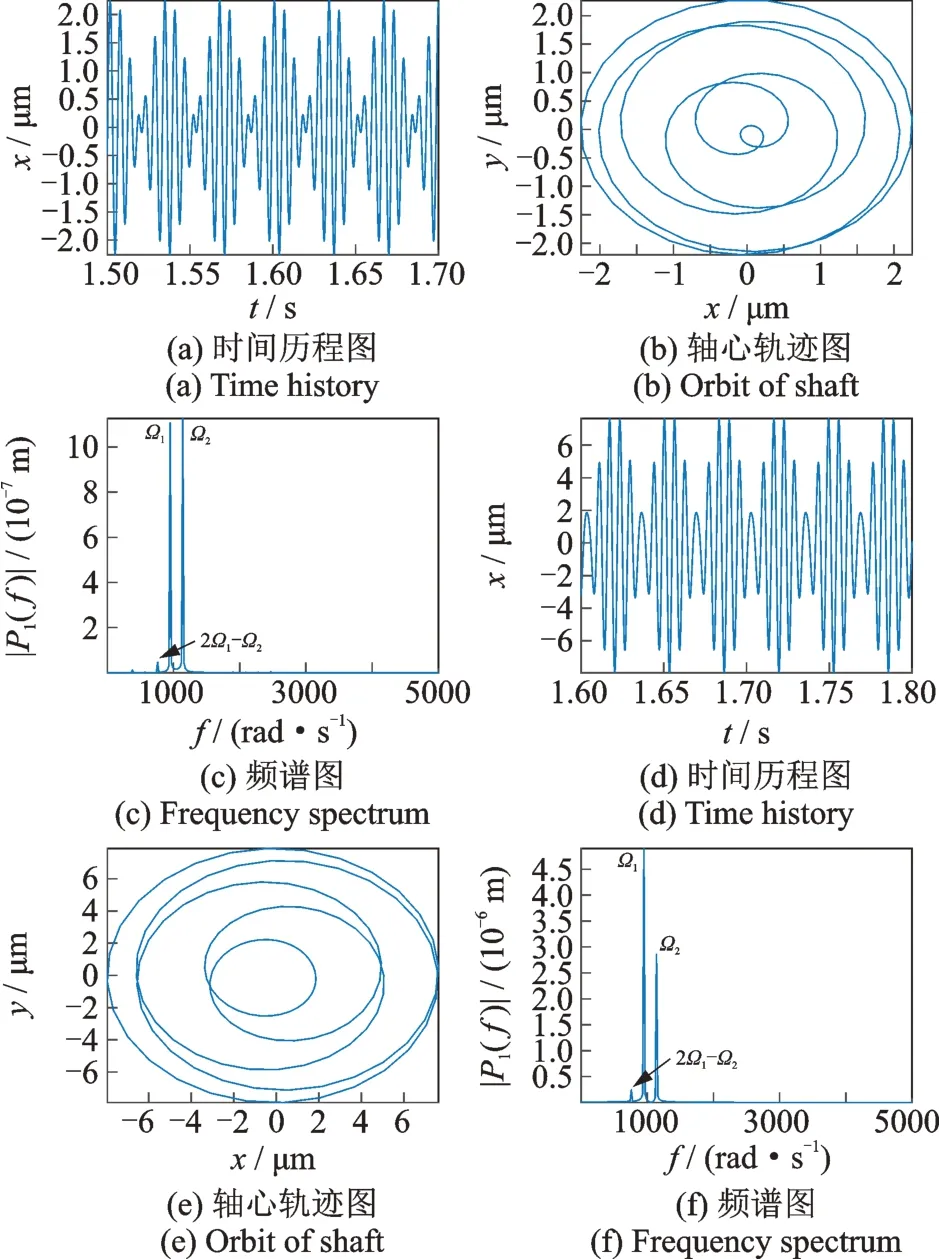
图14 低压涡轮(a)~(c)与高压涡轮(d)~(f)在ω=950 rad/s,δ=1 μm 下的时间历程图、轴心轨迹图与频谱图Fig 14 Time history,orbit of shaft and frequency spectrum of low pressure turbine(a)~(c)and high pressure turbine(d)~(f)at ω=950 rad/s,δ=1 μm
由图14 可知,当δ=1 μm 时,高低压转子涡轮处均分别以高低压转子的不平衡激励频率Ω1,Ω2占主导,组合频率2Ω1-Ω2的作用很微弱,此时的轴心轨迹为相叠加的圆环。由图15 可见,当增大间隙时(δ=5 μm),除了高低压转子的不平衡激励Ω1,Ω2外,组合频率2Ω1-Ω2的作用开始变得明显,而高压转子的不平衡激励Ω2引起的幅值开始减小。由图16 可见,在δ=10 μm 时,除了2Ω1-Ω2以外,还出现了Ω2-Ω1,2Ω2-2Ω1,2Ω2-Ω1等组合频率成分,其中,高低压涡轮的情况有所不同:低压涡轮此时仍然以低压不平衡激励Ω1为主导,而高压涡轮则是以组合频率2Ω1-Ω2为主导,通过计算可知,此时组合频率2Ω1-Ω2的值为760 rad/s,与整机系统第一阶临界转速760 rad/s 重合,因此950 rad/s 位置处的共振峰为组合频率2Ω1-Ω2引起的组合共振。此外,低压涡轮中组合频率Ω1+Ω2的作用较明显,而高压涡轮中组合频率Ω1+Ω2的成分十分微弱。另外,高低压涡轮的轴心轨迹随着中介轴承间隙的增加都变得较为混乱。

图15 低压涡轮(a)~(c)与高压涡轮(d)~(f)在ω=950 rad/s,δ=5 μm 下的时间历程图、轴心轨迹图与频谱图Fig.15 Time history,orbit of shaft and frequency spectrum of low pressure turbine(a)~(c)and high pressure turbine(d)~(f)at ω=950 rad/s,δ=5 μm

图16 低压涡轮(a)~(c)与高压涡轮(d)~(f)在ω=950 rad/s,δ=10 μm 下的时间历程图、轴心轨迹图与频谱图Fig.16 Time history,orbit of shaft and frequency spectrum of low pressure turbine(a)~(c)and high pressure turbine(d)~(f)at ω=950 rad/s,δ=10 μm
3 中介轴承间隙对机匣非线性振动特性的影响
中介轴承的间隙对于双转子的非线性振动特性有较为明显的影响,但在实际的航空发动机中,难以直接监测到转子的信号,往往只能在机匣上布置测点,那么机匣上的信号是否能够切实地反映内部双转子的现象以及机匣测点的位置是否对监测效果有影响都是值得考虑的问题。
机匣前测点Ⅰ的幅频响应如图17所示,对比机匣前测点和高低压转子的幅频响应曲线(如图5~9),可以看出机匣的振动的幅值相较于转子而言小2 个数量级,因此机匣上的信号其实是十分微弱的,但是机匣前测点的振动响应随着中介轴承间隙的变化规律与高低压转子的规律相类似:当中介轴承间隙增大时,临界转速略微减小,双稳态区间增大,共振峰幅值略微减小,其中第2 个共振峰减小的幅度比第1 个共振峰大;当中介轴承间隙δ=14 μm 时,第二个共振峰消失。但是在高低压转子出现组合频率的转速下,前测点组合共振峰峰值很小。做出机匣前测点在ω=950 rad/s,δ=10 μm 时的时间历程曲线以及频谱图如图18所示,可以发现此时机匣前测点虽然有组合频率成分2Ω1-Ω2,但该频率成分并未占据主导地位,此时前测点的振动主要是受到低压转子不平衡激励Ω1的影响,在对应的转速下,并不能反映内部双转子的所有组合频率。

图17 机匣前测点Ⅰ的幅频响应图(实线为升速曲线,虚线为降速曲线)Fig.17 Amplitude-frequency response of front casing pointⅠ(full lines are run up,dotted line are slow down)

图18 机匣前测点Ⅰ在ω=950 rad/s,δ=10 μm 下的时间历程图与频谱图Fig.18 Time history and frequency spectrum of front casingpointⅠat ω=950 rad/s,δ=10 μm
机匣中测点和后测点的幅频响应分别如图19,20所示,可以发现中后测点的幅频响应规律较为相似,能够体现出高低压转子振动响应的相应规律,且振动的幅值是比前测点大的。并且在低压转子转速950 rad/s 的条件下,也出现了较明显的组合共振峰。绘出机匣中测点与后测点在ω=950 rad/s,δ=10 μm 时的时间历程曲线及频谱图,分别如图21 和22所示。可以发现中测点的频谱图与高压涡轮的频谱(图16(f))相比,都是由组合频率2Ω1-Ω2占主导作用,但机匣中测点的频谱中缺少了Ω2-Ω1,3Ω2-3Ω1这两种频率成分,却多出了Ω1+Ω2这一频率成分,这个频率成分在低压涡轮上(图16(c))能够观测到,但不明显。对比图21 和22,可以发现机匣后测点相较于机匣中测点也有所不同:首先是机匣中测点的频率成分中,低压转子不平衡激励频率Ω1的成分的幅值比高压转子不平衡激励频率Ω2成分的幅值更大,在后测点则情况相反,高压转子不平衡激励频率Ω2成分的幅值更大,其次机匣后测点的频谱图中相对于中测点缺少了2Ω2-2Ω1这一频率成分。机匣不同部位对不同频率成分的敏感度不同,高低压转子上的振动传递到机匣后一些频率成分衰减得多,一些频率成分衰减得少,因此转子上一些比较明显的频率成分在机匣上表现的不明显,而一些在转子上不容易观察到的频率成分反而在机匣上更明显。

图19 机匣中测点Ⅱ幅频响应图(实线为升速曲线,虚线为降速曲线)Fig.19 Amplitude-frequency response of middle casing pointⅡ(full lines are run up,dotted line are slow down)
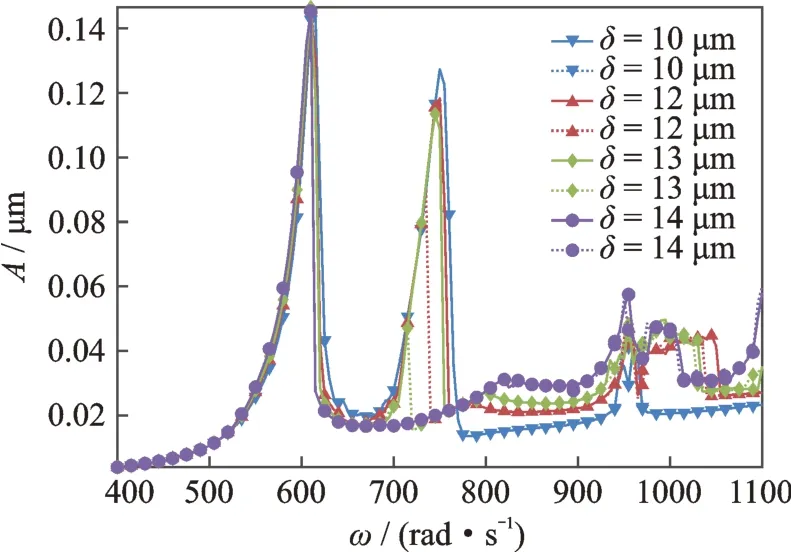
图20 机匣后测点Ⅲ幅频响应图(实线为升速曲线,虚线为降速曲线)Fig.20 Amplitude-frequency response of rear casing pointⅢ(full lines are run up,dotted line are slow down)

图21 机匣中测点Ⅱ在ω=950 rad/s,δ=10 μm 下的时间历程图与频谱图Fig.21 Time history and frequency spectrum of middle casing point Ⅱat ω=950 rad/s,δ=10 μm
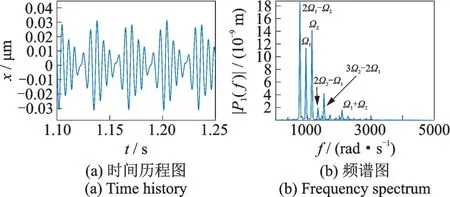
图22 机匣后测点Ⅲ在ω=950 rad/s,δ=10 μm 下的时间历程图与频谱图Fig.22 Time history and frequency spectrum of rear casing point Ⅲat ω=950 rad/s,δ=10 μm
综合对比机匣前中后测点的情况,可以发现机匣测点位置不同所能监测到的现象是不同的,前测点虽然能够观察到振动突跳及双稳态等现象,但在双转子内部发生组合共振时,机匣前测点的组合共振峰幅值不明显,频率成分少。机匣中后测点在内部双转子发生振动突跳、双稳态及组合共振现象时均有类似现象产生。但中后测点情况也不同,机匣中测点的振动幅值大于机匣后测点,且机匣中测点在组合共振时能监测到的相关组合频率成分也比机匣后测点的更为丰富。根据以上对比,该机型的机匣测点安排应为机匣中测点最优,机匣后测点其次,最后是机匣前测点。
4 结论
本文以某型号航空发动机整机振动试验台为研究对象,考虑了中介轴承Hertz 接触非线性,建立了简化的整机系统非线性动力学模型,采用Newmark-β 与Newton-Raphson 结合的方法求解整机系统的非线性振动响应,着重分析了中介轴承间隙对整机系统非线性振动特性的影响规律,主要结论如下:
1)中介轴承的间隙对整机系统的非线性振动特性影响显著,增大间隙能够产生丰富的非线性现象。当中介轴承间隙由1 μm 增大到10 μm 时,整机系统振动响应中出现丰富的组合频率(mΩ1±nΩ2)成分,其中组合频率2Ω1-Ω2逐渐占据主导地位,进而引发组合共振(低压转子转速950 rad/s)。当中介轴承间隙增加到12 μm,低压转子不平衡激励激起的共振峰会产生振动突跳与双稳态现象,高压转子不平衡激励激起的共振峰则没有这些现象。在此基础上继续增大间隙时,共振峰幅值会略微减小,共振峰对应的转速也会略微减小,而双稳态区间会增大。
2)中介轴承的间隙对高低压转子振动的耦合程度有一定影响。增大中介轴承间隙,高低压转子的耦合程度会降低,当中介轴承间隙到达14 μm 时,高低压转子的耦合程度会极大下降,导致低压转子不平衡激励在第1 阶临界转速下激起的共振峰“消失”。
3)机匣上的振动信号可以反映出机匣内部高低压转子的振动情况,但机匣上不同位置测点的情况不同。当双转子出现振动突跳、双稳态以及组合共振现象时,机匣中后测点均能够监测到相应的现象,其中机匣中测点能够监测到的组合频率更为丰富,且机匣中测点监测到的振动幅值也更大,因此当为本机型选择布置机匣测点布置时,机匣中测点最优,机匣后测点次之,最后为机匣前测点。
进一步的研究工作将集中在中介轴承间隙对航空发动机整机系统分岔特性的影响问题。并且考虑更为详细的发动机转子结构,研究振动信号从高低压转子到机匣各测点的振动传递路径问题。
