谐振放大压电声学超材料梁带隙特性研究
2022-07-26陈圣兵宋玉宝贺旭照
陈圣兵,张 浩,宋玉宝,贺旭照
(中国空气动力研究与发展中心,四川绵阳 621000)
引言
近年来,声学超材料受到物理和声学工程领域学者的广泛关注[1-5]。声学超材料是一种具有超常物理特性的人工复合材料,具有产生负质量密度[5]、负弹性模量[2]、负折射[6]、亚波长带隙[7]等特殊性质,被应用于声学斗篷设计[8]、声聚焦[4]、振动与噪声控制[9]等领域,具有较大的科学研究价值和工程应用背景。特别是声学超材料具有的亚波长带隙可以实现小尺寸结构控制大波长弹性波[1],对于解决大柔性结构的低频振动与噪声控制问题具有重要意义。
声学超材料的带隙形成主要由内部微振子的局域共振引起,通过设计微振子结构可以得到结构振动与噪声控制中需要的带隙特性。声学超材料内的局域共振特性不仅可以由传统的机械微振子产生[10],还可以引入智能材料,形成具有带隙主动可调能力的智能声学超材料。其中,利用压电分流谐振子产生局域共振带隙的压电声学超材料具有制作简单、稳定性好、调节方便等优点,受到学者的广泛关注。Thorp 等[11]首次将压电分流技术应用于带隙控制,研究了一维杆中弹性波传播的衰减和局域化现象。Spadoni 等[12]将压电分流技术推广到二维薄板中弹性波带隙的调控,其研究结论被Casadei 实验验证[13]。Airoldi 等[14]提出了一种一维可调谐压电声学超材料设计方案,通过理论研究和实验验证证明了压电分流谐振子对带隙调控的有效性。本文作者也在压电声学超材料领域开展了大量的研究工作,从算法设计、机理研究、实验验证等多个方面对压电声学超材料进行了较为深入的分析和系统的总结[15-16]。传统的压电分流声学超材料一般采用被动谐振电路,受到压电材料机电耦合能力的限制,带隙一般较窄,难以满足低频宽带振动与噪声控制的工程需求。因此,为了增大带隙宽度,本文提出利用模拟放大电路对压电片信号进行放大,然后再连入谐振电路形成局域共振,以实现局域共振效果的增强,从而增大带隙宽度。
本文以一维压电声学超材料梁为研究对象,将压电片划分为传感极和驱动极,其中传感极得到的输入电压通过正向运算放大电路进行放大,再与一个分流电感相连构成谐振回路。采用有限元方法对压电声学超材料梁带隙特性进行求解,分析了带隙随放大倍数的变化和等效弹性模量随频率的变化。最后,利用商用有限元软件建立了有限周期超材料梁模型,仿真分析了有限周期超材料梁的振动传递特性,验证了带隙计算的正确性。
1 数学建模
压电声学超材料梁布局如图1所示,可以看作是由单个元胞沿着轴向平移形成的一维超晶格结构,每个元胞包含基体梁、压电片和谐振放大电路。两个相同的压电片分别布置在基体梁的上下表面相同的位置,压电片上敷设有三等分条状电极(图中深灰色所示),电极之间留有间隙,其中中间电极部分(S)作为传感极,两边电极部分(A)作为驱动极。传感极输出电压通过正向放大电路后,与一个分流电感串联,然后再施加到驱动极进行驱动,可以实现谐振分流放大功能。压电声学超材料梁具有周期性,因而只需要对单个元胞进行动力学分析,结合Floquet 定理就可以得到整个一维梁中的弯曲波传播特性。

图1 压电声学超材料梁布局示意图Fig.1 Sketch of the acoustic metamaterial beam
文中压电声学超材料梁元胞如图2所示。从图中可以看出压电片传感极(S)输出电压u1通过一个运算放大电路后得到驱动电压u2,然后与一个分流电感L串联,输出电压u3连接压电片驱动极,实现放大输出回路的谐振和驱动,在基体内形成局域共振带隙效果。

图2 压电声学超材料梁元胞Fig.2 Unit cell of the acoustic metamaterial beam
1.1 带隙计算
运算放大电路中,利用运算放大器的虚短和虚断特性,结合欧姆定律可以得到运算放大电路的输出电压u2与输入电压u1之间的关系为:
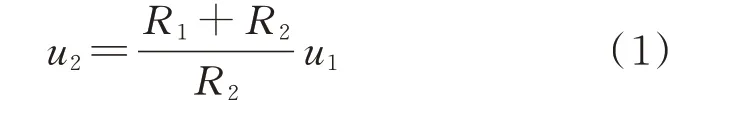
因此,运算放大电路的放大倍数λ为:

谐振回路中,由基尔霍夫定律可知:
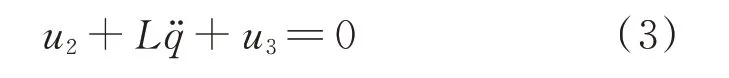
式中q为压电片驱动极上的总电荷。
压电片为压电陶瓷材料,极化方向为厚度方向,以应力T和电场E为自变量,应变S和电位移D为因变量,相应的压电方程可以写成分量形式:
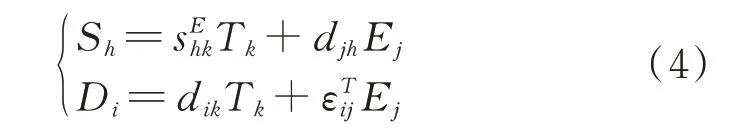
式中i,j=1,2,3;h,k=1,2,…,6;sE为短路柔度系数矩阵;d为压电应变常数;εT为恒应力介电常数。
采用有限元方法对压电声学超材料梁的元胞进行建模,单元类型为二阶六面体单元,如图3所示,根据节点位置将自由度分别标示为L(左端)、R(右端)和I(内部)。因此,利用Hamilition 原理和标准的有限元建模方法可以得到离散形式的压电控制方程为:
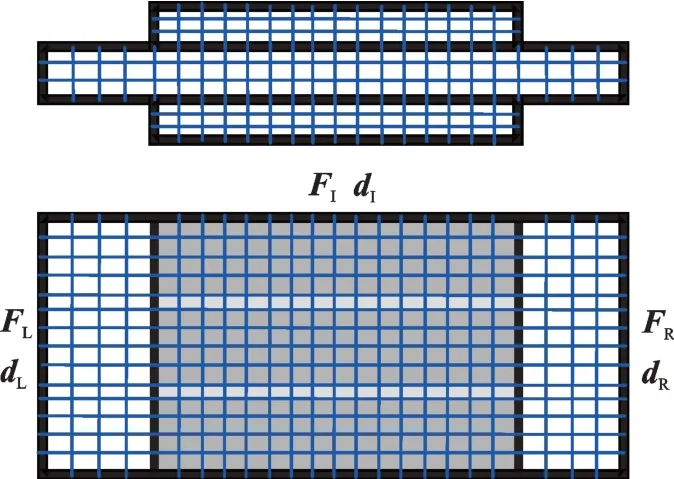
图3 元胞有限元网格划分Fig.3 Mesh of unit cell
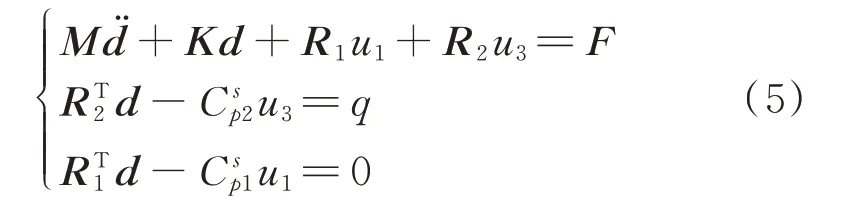
式中d=[dLdIdR] 为节点位移向量,F=[FLFIFR]为节点力向量,M为质量矩阵,K为刚度矩阵,R1和R2分别为传感极压电片和驱动极压电片机电耦合向量,q为驱动极总电荷,和分别为传感极和驱动极压电片的恒应变电容。
将式(1)和(3)代入方程(5)整理得:

其中:


假设压电声学超材料梁的运动为频率ω的简谐运动,那么方程(6)可以改写为:
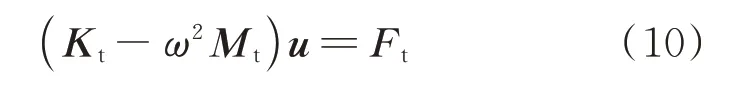
压电声学超材料梁具有周期性,因此元胞边界条件可以根据Floquet 定理得到:
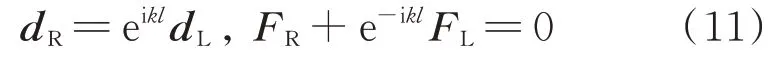
式中k为波数,l为晶格常数,。
将式(11)代入式(10),整理为特征值形式:

式中S为特征矩阵,为波数k的函数,I 为单位矩阵,。
最后,通过在不可约布里渊区扫略波数k,求解特征方程(12)得到特征频率ω,可以获得压电声学超材料梁的能带结构。
1.2 等效参数
等效参数是分析声学超材料的重要手段,对于如图2所示的声学超材料梁元胞,不考虑梁的三维效应影响,假设压电片除了垂直于轴向的端面外,其余表面都自由,且压电片只有厚度方向电场作用,那么压电方程(4)可以简化为:
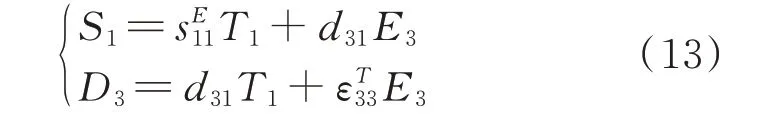
式中T1和S1分别为压电片沿轴向的应力和应变,D3和E3分别为压电片电极上的电位移和内部电场,为短路柔顺系数,为厚度方向恒应力介电常数,d31为压电应变常数。
压电片传感极上电位移为零,那么由方程(13)可得传感极压电片内电场为:
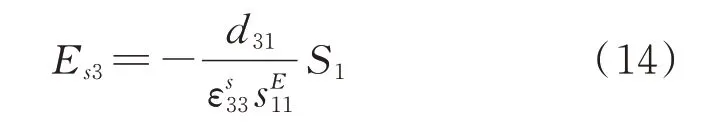

将式(14)代入式(13),可以得到传感极压电片等效弹性模量,表示为:

传感极压电片内电场与输出电压u1之间的关系为:

式中hp为压电片厚度。
联立式(14)和(17)可以得到传感极输出电压,表示为:

对于驱动极压电片,同样采用压电方程(13)可得驱动极电位移为:

式中Ea3为驱动极压电片内电场。
驱动极压电片内电场与输入电压u3之间的关系为:

采用长波假设,即压电片内应变和电极上电位移近似处处相等,那么驱动极上的电荷q可以写成:

式中As为驱动极压电片电极面积。
假设压电片的运动为频率ω的简谐振动,整理得到驱动极压电片内电场,表示为:

将式(22)代入式(13)可得驱动极压电片等效弹性模量为:

对等效弹性模量进行归一化处理,定义归一化等效弹性模量为:

为了分析等效模量对声学超材料梁带隙的影响,需要进一步推导得到超材料梁的等效弯曲刚度。从图2 可以看出,超材料梁是由压电片和基体梁形成的复合梁,其弯曲刚度可以表示为:

式中Is,Ia和Ih分别为传感器压电片、驱动极压电片和基体梁的横截面惯性矩。
超材料梁弯曲刚度受到电路放大倍数λ的影响,为了方便分析,将复合梁的等效弯曲刚度对λ=0 的值进行归一化处理得:
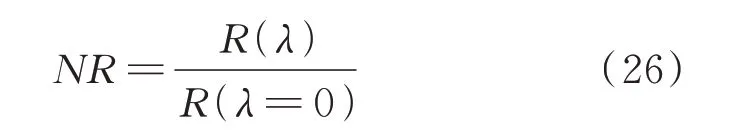
2 算例与讨论
算例中,压电声学超材料基体梁为铝,压电片材料为PZT-5H。元胞几何参数如下:元胞晶格常数为40 mm;基体梁宽度为20 mm,厚度为2 mm;压电片长度为30 mm,厚度为0.5 mm,宽度为20 mm,传感极和驱动极的宽度都为6 mm,传感极与驱动极之间留有1 mm 间隙。电路参数中,L=0.8 H。
采用文中带隙计算方法和参数计算得到谐振放大压电声学超材料梁能带结构如图4所示,分别计算了谐振放大电路开路和放大倍数情况下色散曲线的变化情况。
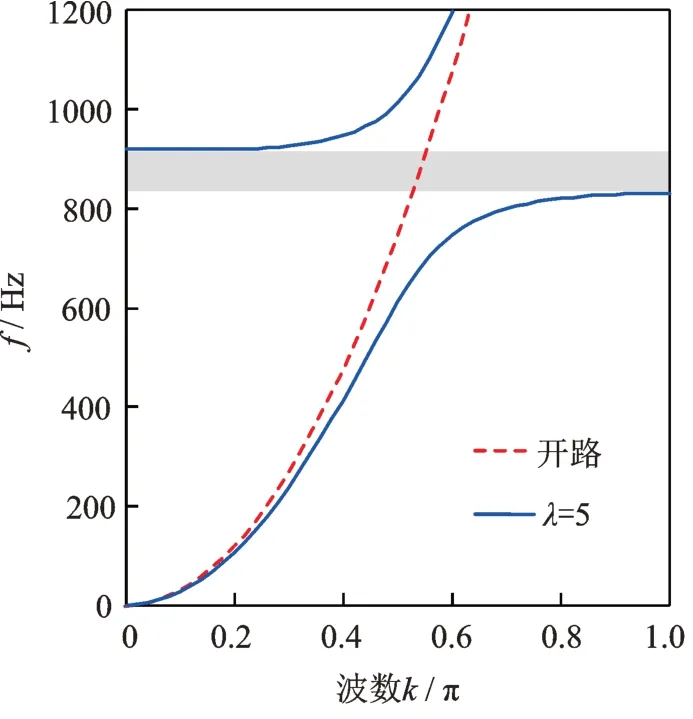
图4 压电声学超材料能带结构Fig.4 Band structure of the acoustic metamaterial beam
从图4 中可以看出,谐振放大电路开路时,压电声学超材料梁中没有局域共振单元,没有局域共振带隙出现;谐振放大电路闭合,且λ=5 时,受到谐振电路的局域共振作用,压电声学超材料梁内出现了一个局域共振带隙,带隙位置为831~920 Hz,带隙宽度为89 Hz。因此,文中提出的谐振放大电路可以在梁内产生局域共振带隙。
局域共振带隙随放大倍数的变化如图5所示,图中实线为带隙上边界频率,虚线为带隙下边界频率。
从图5 中可以看出,带隙上下边界频率都是随着放大倍数λ的增大而降低,但是带隙下边界降低得更快,因而带隙宽度是随着放大倍数增大而增大的,从λ=0 时的15 Hz 增大到λ=10 时的162 Hz。特别是当λ=0 时,放大电路失去作用,电路退化为普通的谐振分流电路,带隙宽度要远比谐振放大电路形成的带隙宽度窄。因而,谐振放大电路经过电压放大后,与传统谐振分流电路相比,不仅可以使谐振频率降低,还可以大大提高带隙宽度,形成低频宽度带隙。
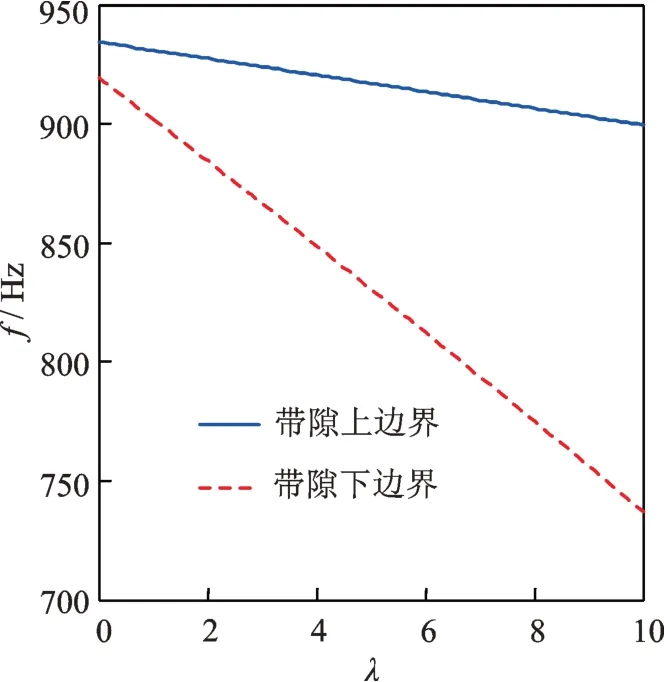
图5 带隙随放大倍数的变化Fig.5 Variation of band gap with amplification coefficient
驱动极压电片等效弹性模量随频率的变化如图6所示。从图中可以看出,等效弹性模量随着频率的增大而减小,在谐振频率附近变为负值并趋于负无穷大,然后跳跃到正无穷大并逐渐减小。通过对比带隙位置和负等效模量出现位置,可以看出负等效模量是带隙形成的主要原因,但受到基体梁的影响,驱动极压电片较小的负模量还不足以形成局域共振带隙。因而,局域共振带隙的上边界和负模量频率上边界相近,而下边界比负模量下边界频率高很多。
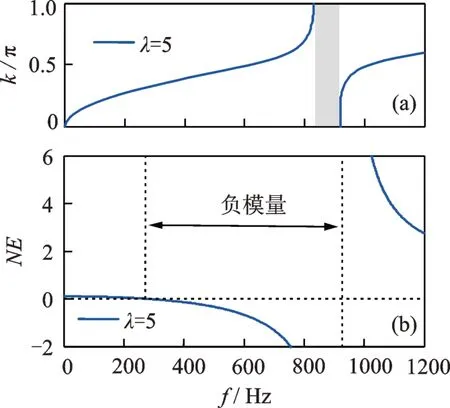
图6 等效弹性模量随频率的变化Fig.6 Variation of equivalent modulus with frequency
进一步分析超材料梁等效弯曲刚度随频率的变化如图7所示。从图中可以看出等效弯曲刚度的变化趋势与驱动极压电片等效弹性模量变化(参看图6)相似,主要不同在于负刚度起始频率比负模量起始频率高很多,而负刚度终止频率与负模量终止频率相同。显然,负刚度产生的区域与带隙产生位置基本一致。因此,通过对压电片等效弹性模量和梁等效弯曲刚度的分析可以发现:压电片的负等效模量是带隙形成的诱因,但是受到基体梁的影响,压电片较小的负等效模量不足以抵消基体梁的弯曲刚度而形成负等效弯曲刚度,只有压电片负模量增大到一定值后才能使整个复合梁呈现负等效刚度,这也是带隙起始频率要远大于压电片负等效模量起始频率的原因。复合梁的负等效刚度是带隙形成的直接原因,两种频率基本一致。
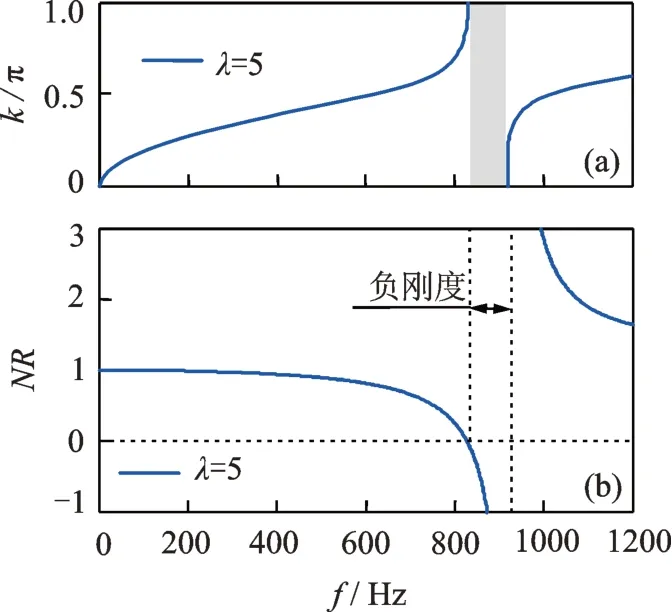
图7 等效弯曲刚度随频率的变化Fig.7 Variation of equivalent rigidity with frequency
为了验证带隙计算的正确性,在商用有限元软件中建立了10 周期压电声学超材料梁仿真分析模型,如图8所示。电路放大倍数λ=5,分流电感L=0.8 H。在梁的一端施加单位幅值横向力激励,利用频响分析得到梁的两端位移幅值,计算得到0~1200 Hz 内压电声学超材料梁的振动传递特性。

图8 有限元仿真模型Fig.8 Finite element simulation model
为了确保有限元仿真结果可靠,分别采用不同的网格密度对仿真收敛性进行了分析。网格采用六面体二阶拉格朗日插值单元,选择三种网格密度进行网格划分,单元数N分别为700,2240 和5610。计算得到超材料梁的振动传递特性如图9所示,可以看出网格数为2240 和5610 计算得到结果基本一致,表明当网格数为2240 时结果已经趋于收敛。
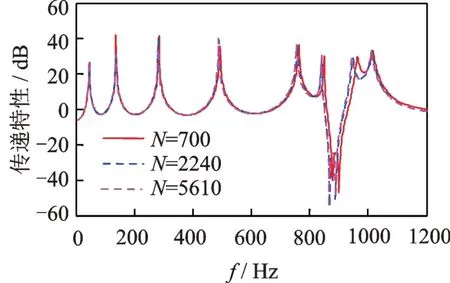
图9 仿真收敛性Fig.9 Convergence of simulation
商业有限元软件仿真结果与理论计算结果对比如图10所示。其中,图10(a)所示为理论求解元胞色散曲线得到的带隙位置,图10(b)所示为仿真软件利用频响分析得到的10 周期梁振动传递特性,对比两图可以看出,在带隙位置振动传递出现了较大衰减,证明了带隙对振动传递抑制的有效性,也验证了文中带隙理论计算方法的正确性。
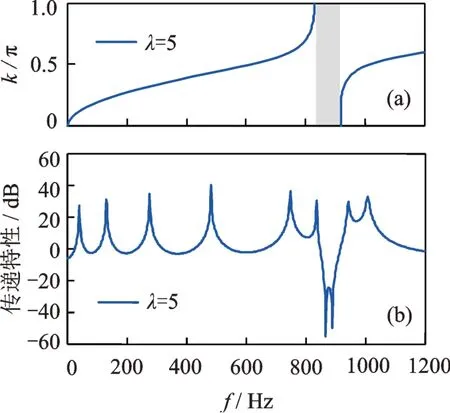
图10 压电声学超材料梁振动传递特性Fig.10 Vibrational transmission properties of the acoustic metamaterial beam
3 带隙展宽特性分析
从理论分析和软件仿真结果可以看出,谐振放大电路可以有效拓展带隙宽度,使带隙宽度从λ=0时的15 Hz 增大到λ=10 时的162 Hz。为了对谐振放大电路的带隙展宽性能进行评估,进一步开展了谐振放大电路与传统带隙展开方法的性能对比分析。
压电声学超材料的传统带隙展宽方法主要包括带隙耦合[17]、尺寸[17-18]及压电片形状[19]优化等。带隙耦合主要通过改变基体材料或晶格参数,使布拉格带隙与局域共振带隙形成耦合;尺寸及形状优化主要通过增大压电片面积或改变压电片外形,提高压电片机电耦合能力;负电容放大电路是通过引入负电容来提高压电片等效机电耦合系数。
针对文中一维压电声学超材料梁,分别采用三种方法对带隙进行展宽,包括带隙耦合、尺寸优化和谐振放大。其中,带隙耦合通过修改晶格常数实现布拉格带隙与局域共振带隙耦合,将晶格常数从40 mm 增大到75 mm;尺寸优化通过增大压电片长度实现,从30 mm 增大到40 mm;谐振放大通过改变放大倍数实现,放大倍数从0 增大到10。最终得到的带隙展宽效果如表1所示,可以看出三种方法都可以展宽带隙宽度,其中尺寸优化效果较差,文中提出的谐振放大效果最好,带隙耦合也产生了较好的效果。不同的带隙展宽方法都有其优缺点:带隙耦合的优点是不需要外部能量输入,稳定可靠,带隙展宽效果较好,缺点是尺寸大,难以实现小尺寸控制大波长;尺寸优化的优点是简单可靠,通过增大压电片尺寸提高机电耦合能力,不需要外部能量输入,缺点是带隙展宽能力较差;谐振放大的优点是带隙展宽效果非常好,尺寸较小,调节方便,缺点是需要外部能量输入。

表1 带隙展宽效果对比Tab.1 Comparison of band broadening effects
因此,文中提出的谐振放大电路具有较好的带隙展宽效果,尤其是对于结构尺寸受限,需要利用局域共振带隙实现小尺寸控制大波长的时候,谐振放大具有非常大的优势。
4 结论
本文提出了一种谐振放大压电声学超材料梁,将压电片划分为传感极和驱动极,传感极输出电压经过运算放大电路放大,然后与谐振电路相连,实现局域共振效果的增强,从而增大带隙宽度。与传统压电分流声学超材料相比,谐振放大压电声学超材料梁增加了电压放大环节,可以有效增强谐振回路的局域共振效果,改善带隙宽度。随着放大倍数的增大,带隙宽度从λ=0时的15 Hz增大到λ=10时的162 Hz。等效模量分析结果表明负等效模量是带隙形成的主要原因,但较小的负模量不足以形成局域共振带隙,局域共振带隙的上边界和负模量频率上边界相近,而下边界比负模量下边界频率高很多。最后,利用商用有限元软件仿真分析了有限周期压电声学超材料梁的振动传递特性,在带隙位置振动传递特性出现了较大衰减,证明了带隙对振动传递抑制的有效性,也验证了文中带隙计算方法的正确性。
