智能压电材料MFC在太阳电池阵帆板上的主动抑振研究

骆海涛，吴星元，刘广明，富 佳

（1.中国科学院沈阳自动化研究所机器人学国家重点实验室，辽宁沈阳 110016；2.中国科学院机器人与智能制造创新研究院，辽宁沈阳 110169；3.沈阳理工大学机械工程学院，辽宁沈阳 110159）

引言

在空间环境中，太阳电池阵在轨展开、对日定向调整和受到航天器机动变轨所产生的干扰，均会使得电池阵的帆板产生振动。太阳电池阵为薄壁结构，由于自身几何尺寸大和材料非线性大变形的特性使得电池阵柔度增大，而太空环境为低阻尼的状态，振动难以得到快速衰减，长时间的持续振动会造成敏感器件的破坏，航天器需要更长的时间和消耗更多的燃料来进行姿态调整，还会影响到航天器或卫星本体的指向精度和姿态稳定，对其姿态控制和工作造成极其不利的影响。因此，为了保证航天器或卫星的指向精度和姿态稳定，对太阳电池阵振动的快速抑制势在必行。

国内外关于电池阵主动抑振问题已有一定的研究，其中华南理工大学邱志成老师团队对电池阵系统建立了特征模型，并通过线性二次型（Linear Quadratic Regulator，LQR）控制［1］和正位置反馈控制（Positive Position Feedback，PPF）控制［2-4］验证了主动控制的可行性。Omidi等［5］提出了改进的正位置反馈控制（Modified Positive Position Feedback，MPPF）。Williams 等［6］基于MFC 设计了主动控制系统，用于悬臂梁的主动抑振。Sharma 等［7］详细研究了压电材料在不同工作模式下的驱动电压，以及相应的极化方向。Vishal等［8］提出了一种用形状记忆合金丝作驱动器的悬臂梁振动主动抑制方法，将压电纤维增强复合材料应用于悬臂梁的主动抑振中［9］。关于悬臂梁主动控制中的致动器分布位置的研究，Guzmán 等［10］提出了一种拓扑优化的致动器分布方法。Wang 等［11］使用光学相机监测悬臂梁振动，通过Lyapunov 方法进行系统闭环稳定及主动控制时的模型预测［12-14］。在主动抑振系统中，多是基于小型悬臂梁的系统验证，大型太阳电池阵的控制系统应用很少，实际太阳电池阵由于结构复杂，面临太空中的各种扰动，振动情况尤为复杂。悬臂梁单端固定的分析方法与实际帆板的铰链安装方法也有很大的区别，一些对于数学模型依赖较高的算法即使在悬臂梁试验效果良好，应用到工况复杂的帆板上仍然面临严峻的挑战。

本文针对太阳电池阵系统振动控制问题，设计了一套基于MFC 的振动主动控制系统。分析了MFC 作为传感器和致动器的正逆压电效应机理；基于系统辨识的方法，在实验的基础上建立了电池阵振动的数学模型，通过应变能最大理论确定了MFC最佳粘贴区域；采用PID 自整定的控制算法，确立了分立式MFC 驱动器的振动控制参数，实现了可以独立控制MFC 抑振的目标。

1 抑振机理分析及数学模型建立

1.1 压电纤维复合材料抑振机理分析

压电陶瓷在悬臂梁的振动抑制中有着广泛的应用，但是压电陶瓷本身刚性较大，形变较小，所以NASA 基于压电陶瓷设计了一种新型复合材料即MFC，由于本质是压电陶瓷，所以同样具有正逆压电效应，MFC 具有一定的柔度，同面积的MFC 产生的应变力大于压电陶瓷的十倍。本文基于正逆压电效应，将MFC 作为致动器和传感器，MFC 内部结构较为复杂，是由很多细条的压电陶瓷通过交叉电极相连，这样即使其中的部分压电陶瓷发生断裂，MFC 还是能完成一定的作为致动器或者传感器的工作。MFC 材料的工作原理解析如图1所示。

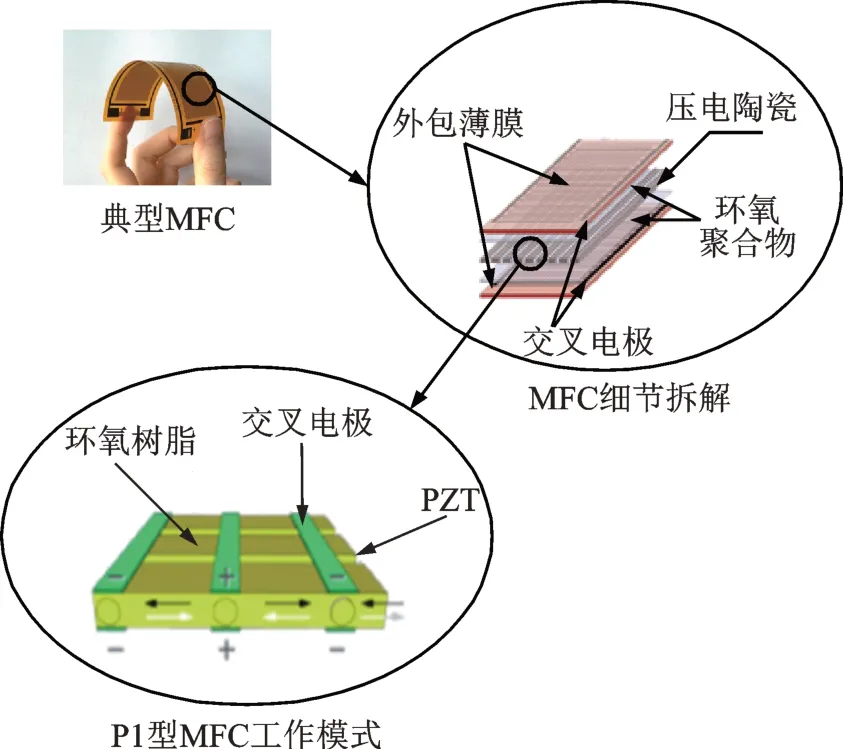
图1 MFC 工作原理Fig.1 MFC working principle

当MFC 作为致动器时，根据逆压电效应，致动器的输出可以用电位移D和电场强度E来描述［15］：

式中 电位移D的单位为C/m2，电场强度E的单位为V/m，Ei和Di（i=1，2，3）的下标表示分量沿参考系的轴向。εii为介电常数，表示介质极化程度，单位为F/m，对于极化后的压电陶瓷材料，只有ε11=ε22≠0 和ε33≠0，则：

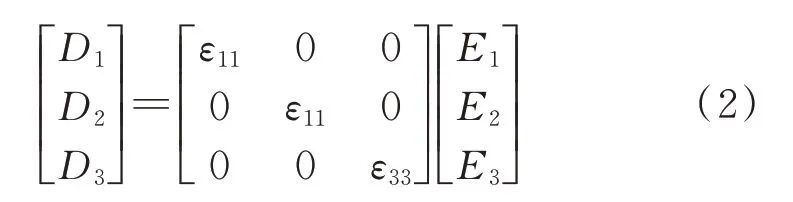
在上述情况下，压电陶瓷的输出也可以用应变S和电场强度E来描述：

式中d为压电应变常数，表示压电元件将机械能转换为电能或者电能转化为机械能的比例常数。对于极化后的压电陶瓷，由于对称性，其压电应变常数矩阵为：

由于d31=d32，d15=d24，因此只有d31，d33和d15三个独立分量。

压电材料的结构应变与应力T之间的关系，根据虎克定律有：

式中Sij为弹性柔顺系数，它是描述介质弹性物理量，单位为m2/N。

根据式（3）和（4）构建联合公式，其分量的形式为：

同理，电位移D则由其承受应力和电场强度产生，其张量分量形式为：

式中diuTu为应力引起的的电位移：为当应力为0 的情况下，由外电场作用产生的电位移，表示应力T=0 或者为常数时的介电常数。

式（5）和（6）是分别以电场强度Ej和应力Tu为自变量的压电方程，也被称为第一类压电方程。当然也有以其他变量构造的其他类的压电方程，本文中以第一类压电方程进行描述。

对于Smart Material 公司生产的MFC，根据电极极化方向的不同，主要制作成以d33和d31效应工作的MFC。本文中选用的两种P1 型MFC 是以d33效应工作的。基于d33效应，当两极施加电压后，压电复合纤维会伸长或者缩短。当MFC 作为致动器时，通过施加在电极上的电压可知此时E3≠0，E1=E2=0，因此将式（5）展开有：

通过上式可知，S4，S5，S6均不反映施加电场后的影响，因此进一步简化该式有：

类似于式（5）展开，将式（6）展开有：

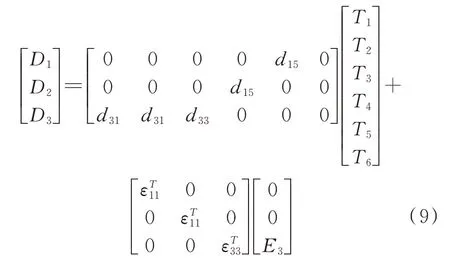
观察上式可知，电位移D1和D2均不反映施加电场后的影响，因此进一步化简该式有：

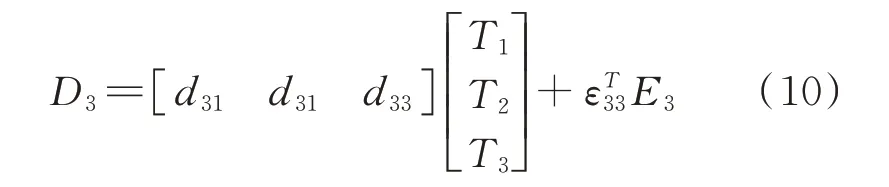
综合式（8）和（10），可以得到MFC 的第一类压电方程：

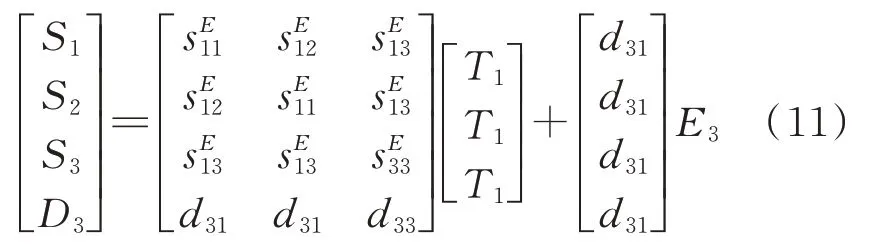
关于MFC 粘贴位置的研究中，多是基于通过有限元建立悬臂板的数学模型，以此作为理论依据来确定MFC 粘贴位置［16］，在本文中，通过MSC.Nastran 软件分析，立足于最大应变能理论确定MFC 最佳粘贴位置。对于帆板模型的结构和材料参数如表1所示。

表1 抑振系统材料参数Tab.1 Material parameters of vibration suppression system

帆板模型的尺寸来源是“向日葵”卫星太阳翼单板的实际尺寸，利用软件分析帆板模型的振动模态，如图2所示，是帆板第1 阶的应变分析图形。通过软件设置采用应变显示选项，从图中可以看到最大应变位置位于末端固定位置以及铰链连接的位置。

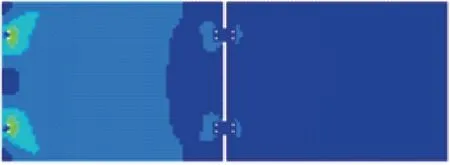
图2 帆板结构第1 阶应变分析Fig.2 The first order strain analysis of sailboard structure

由于应变分布主要集中在帆板结构固定位置，所以第1 阶振型反映了主要的应变集中位置，这些位置也是指导粘贴MFC 的主要依据。表2所示是通过模态分析的帆板前8 阶的振型，主要反映的是各阶的具体振动频率，刚度。

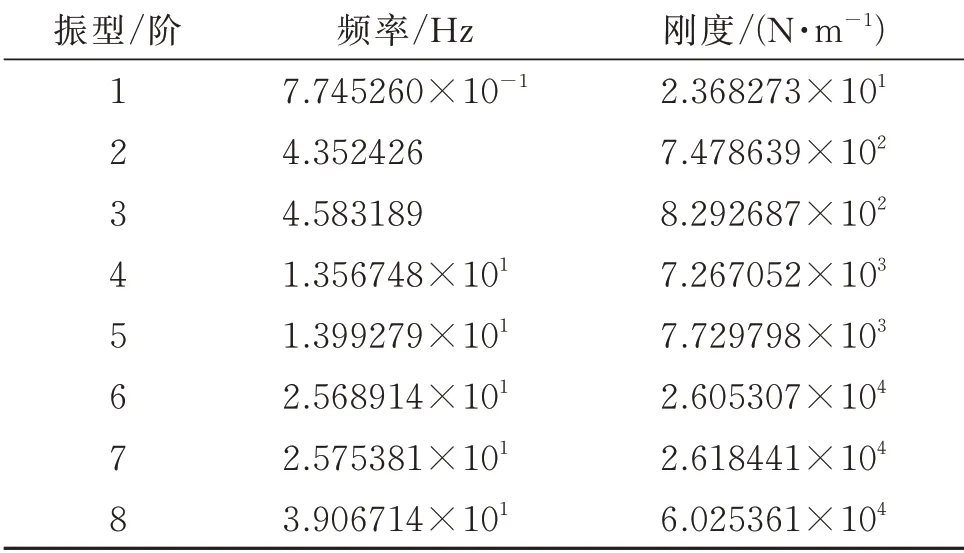
表2 帆板模型模态分析振型表Tab.2 Modal analysis table of sailboard model

1.2 帆板振动数学模型建立

在不考虑板结构非线性的情况下，可以将帆板的振动情况近似为一个2 阶系统［17］。典型的2 阶系统传递函数为：

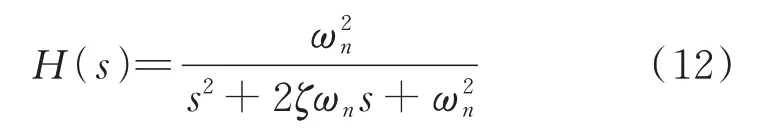
式中ζ为阻尼比；ωn为自由振动频率。

采用系统辨识的思想，通过激光位移传感器测得帆板自由振动的波形。如图3所示是实验帆板安装的位置关系，单板之间通过铰链进行连接。由于激光位移传感器ZLDS103-250的起始量程为65 mm，量程为250 mm，并且帆板振动是基于平衡位置做往复运动，所以帆板和激光位移传感器间距190 mm。

图3 帆板安装位置关系Fig.3 Installation position relationship of sailboard

通过激光位移传感器测得帆板自由振动波形图，如图4所示。数据采集通过LabVIEW 作为上位机，由通过软件模态分析得出的帆板的振型可知，帆板振动的频率很低，所以设置1 KS/s的采样率即采样周期为Tc=0.001 s，足以满足要求。图中，横坐标表示的是采样点数，反映的是时间，纵坐标表示的是振动幅度。

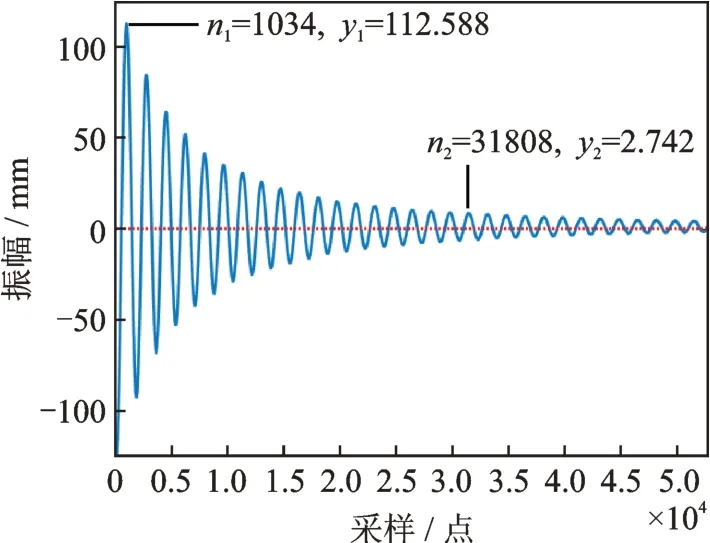
图4 帆板实验测量自由振动波形Fig.4 Measurement of free vibration waveforms in sailboard experiment

已知2 阶系统工作在欠阻尼的情况时，其振动响应为：

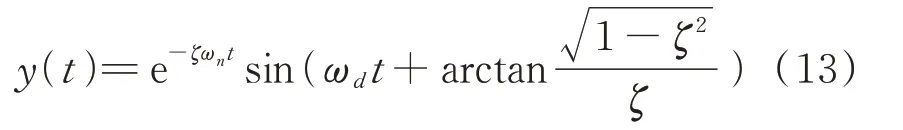
如图4所示的周期为T的自由振动波形中，取t1，t2两个时刻的峰值y1，y2，两个时刻相差k个周期，对应的采样点分别为n1，n2，由式（13）可得：

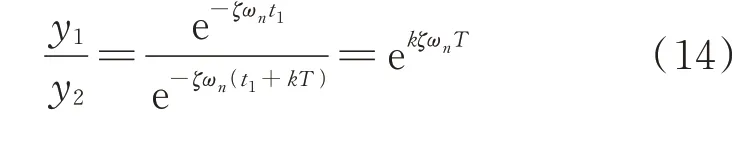
其中：

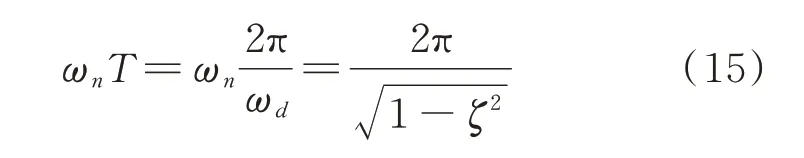
将式（15）代入式（14）中，得到：

选中图中两个点(n1，y1)和(n2，y2)，n1=1034，y1=112.588，n2=31808，y2=2.742，k=18，代入式（16）中，解得阻尼比ζ=0.033。

根据采样点以及采样周期可以求出帆板的振动周期和频率分别为：

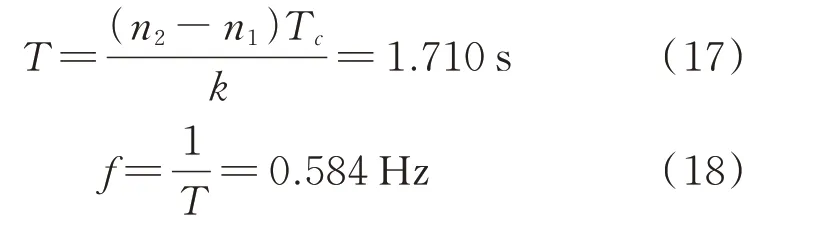
由式（15）可得：

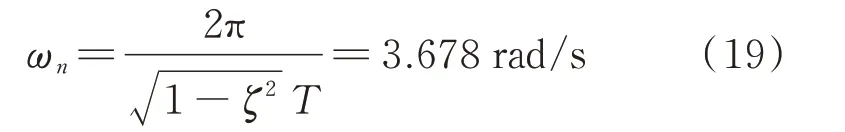
将阻尼比ζ，自由振动频率ωn代入式（12）可得系统的传递函数为

2 主动抑振实验研究

2.1 实验系统介绍

主动抑振系统包括上位机控制系统、信号采集系统、数据转换系统、信号驱动系统、执行机构五部分组成。

上位机控制系统是通过LabVIEW 开发的，上位机主要负责信号处理，由于上位机接收到的是USB-6002 的信号，其中的信息是激光位移传感器输出的0～10 V 的电压信号，通过激光位移传感器对MFC进行标定，这样LabVIEW 处理的信号和Simulink 仿真的信号可以匹配，在Simulink 中计算得到PID 控制参数也就能运用到实际的控制系统中。为了保证初始振动的同一性，需要给出一个固定的初始激振信号。整个上位机控制系统面板如图5所示。

图5 上位机控制面板Fig.5 Upper computer control panel

信号采集系统由MFC 作为传感器和激光位移传感器，主要目的是利用激光位移传感器对MFC 做传感器进行标定，因为在太空中，使用激光位移传感器测位移是不现实的。当MFC 作为传感器时，由于输入电阻的原因，直接测量的电压会失真，所以采用两个1 MΩ 的电阻对MFC 采集的电压分压。USB-6002 测试的最高电压为10 V，将分压后的信号再输入USB-6002 中，这样就可以避免失真。

数据转换系统采用的是NI 公司的数字板卡USB-6002，该板卡能采集8 路分辨率为16 位的模拟信号，最大采样率可达50 KS/s，同时该板卡具有两个16 位D/A 转换输出，适合本实验中应用。

信号驱动系统采用的是适配MFC 的驱动器，是由Smart Material 公司生产的AMD2012-CE2/3驱动板，该驱动板最大输出功率可达4 W，输出电压为-500～+1500 V。

执行机构以MFC 作致动器，本课题使用的MFC 有M-5628-P1 和M-4312-P1 两种类型，极限输出力分别为340 和120 N。整个系统的控制流程图如图6所示。

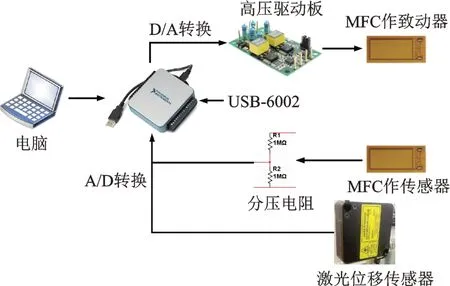
图6 实验系统控制流程图Fig.6 Control flow chart of experimental system

2.2 基于PID 自整定的主动控制算法

在PID 控制中，需要知道控制参数的值，由于PID 设置参数的值一般需要丰富的经验，为了缩短调节参数的时间，将帆板振动的数学模型导入Simulink 中，通过软件模拟的方式，快速得到一组或者几组比较合理的控制参数，这里使用的是PID 自整定的方式，可以快速求得PID 控制参数。

在Simulink 中，绘制PID 自由振动模型及PID控制模块，整体框图如图7所示。

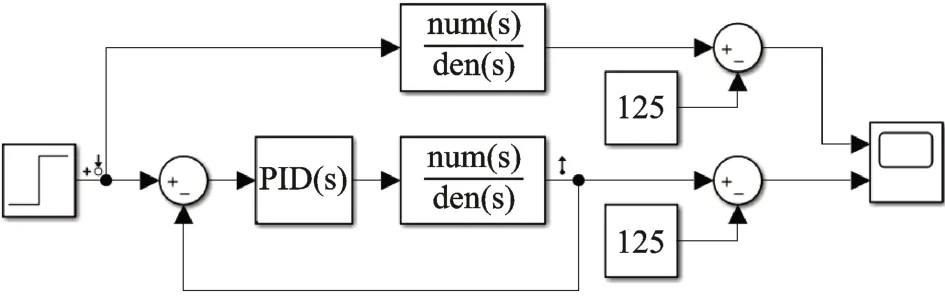
图7 Simulink 参数整定系统框图Fig.7 Block diagram of Simulink parameter setting system

如上图所示，输入信号为一个阶跃信号，其值为：

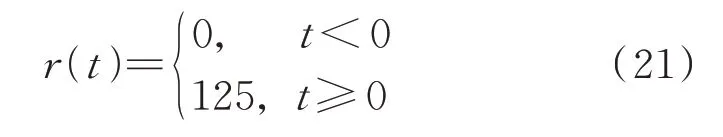
式中的终值125 是激光位移传感器的测量极限范围的1/2，在实验中设为0 点的位置。为了方便观察和理解在结果输入示波器模块前再减125，这样就可以在Simulink 的示波器中观察到测量数据是在以y=0 为基准变化的。

PID 控制的主要依据是通过输入信号r(t)与输出信号y(t)构成控制偏差e(t)，即：

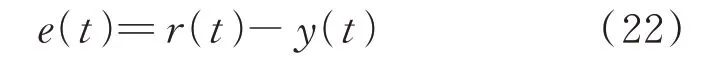
PID 控制器是一种线性控制器，通过线性组合偏差的比例、积分、微分，将三者作为控制量进而控制受控对象。其控制规律为：

其传递函数为：

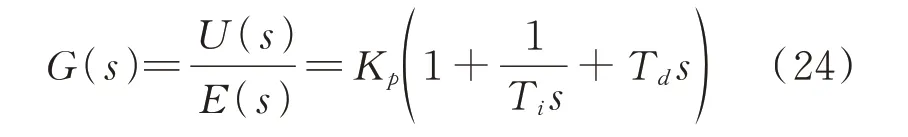
式中Kp为比例系数，Ti为积分时间常数，Td为微分时间常数。

在Simulink 的PID 模块中，传递函数为：

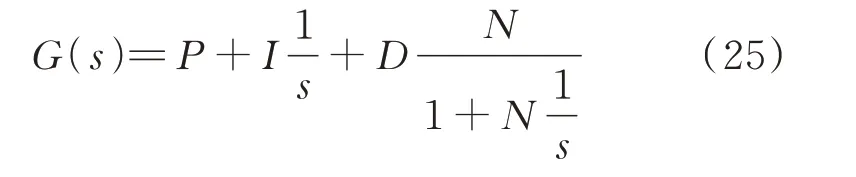
式中P为控制的比例参数，I为积分参数，D为微分参数，N为滤波系数。对比式（24）和（25）可以看到Simulink 的PID 参数和传递函数的系数的差异，所需要的是PID 的参数。

在被控对象模块中输入式（20）的各项系数，输入形式为数组，如图8所示。

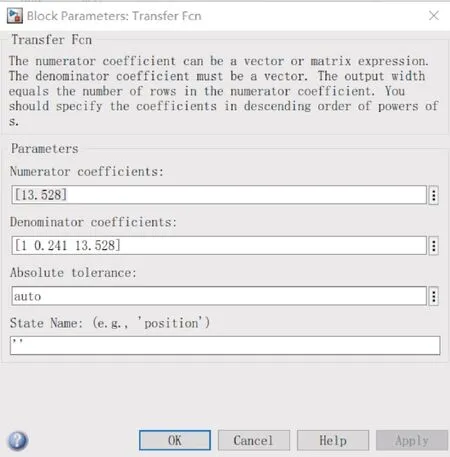
图8 被控对象传递函数输入Fig.8 Transfer function input of controlled object

为了形成控制输入的对比，需要引入两组相同的传递函数，其中一组不引入PID 控制直接输出。

在完成输入模块，PID 模块以及被控对象模块等模块的参数设置之后，便可利用Simulink 进行参数自整定从而得到一组比较合适的PID 控制参数。在Matlab 2020a 中能够比较方便地利用Simulink 的工具包得到想要的的参数。通过Simulink 自整定之后的参数如图9所示。

图9 PID 自整定参数Fig.9 PID self tuning parameters

2.3 太阳能电池阵抑振效果评价

为了保证系统振动的初始激振信号一致，通过前面的实验波形可知，帆板的自由振动波形的频率为0.586 Hz。所以，在上位机中设置激振频率与自由振动的频率相同，激振信号幅值为5 V，频率为0.586 Hz 的正弦信号，如图10所示。

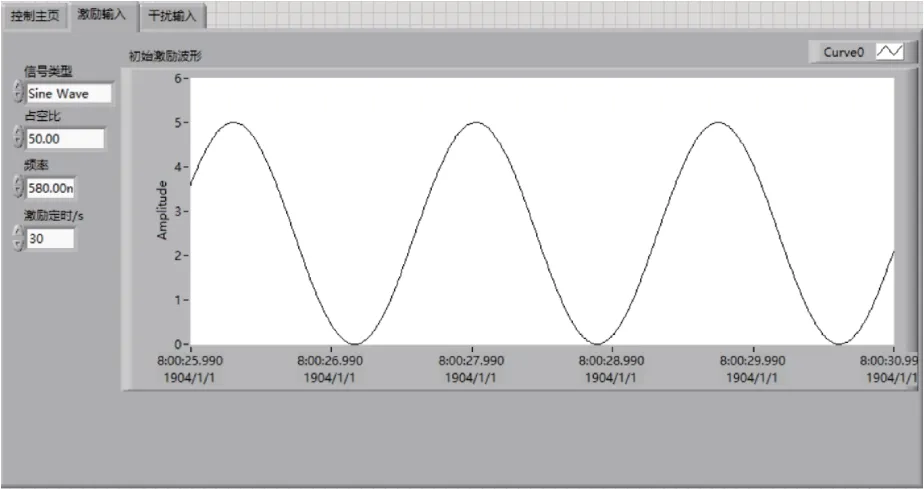
图10 初始激振信号Fig.10 Initial excitation signal

通过上位机，可以采集到的三组振动信号，其中有两组由MFC 作为传感器采集，另一组由激光位移传感器采集，激光位移传感器采集的信号主要用于做参数标定并且保证与MFC 的数据匹配。

由于激光位移传感器的位置定于中轴线上，所以只能采集弯曲振动的信号，而扭转振动的信号可通过传感器MFC 采集。

通过采集的激光位移传感器的信号作为反馈，在LabVIEW 上编写PID 控制程序，由于前期仿真使用实际模型仿真，在Simulink 中通过自整定PID得到的PID 参数为kc=-0.512，ki=0.724，kp=0.424。由于实际模型和在Simulink 中的仿真模型通过前期的参数标定，所以直接将仿真得到的控制参数代入LabVIEW 控制程序中，实验结果如图11所示。

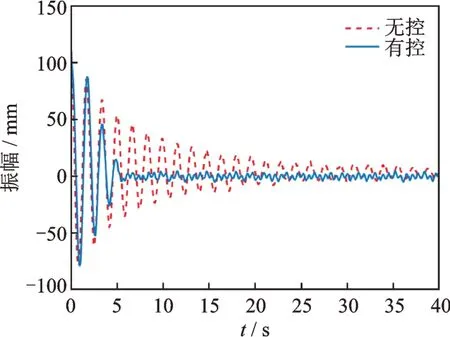
图11 自由振动有无控制实验对比Fig.11 Experimental comparison of free vibration with and without control

为了验证帆板在有干扰的环境下主动抑振效果，分别加入正弦波干扰、白噪声干扰。其中，正弦信号的幅值为5 V，频率为0.586 Hz。图12所示为引入正弦波干扰的情况下，有无控制的波形对比；图13所示为引入白噪声干扰的情况下有无控制的波形对比。

图12 正弦波干扰有无控制对比Fig.12 Comparison of sine wave interference with and without control

图13 白噪声干扰有无控制对比Fig.13 Comparison of white noise interference with and without control

通过实验数据可以看到，自由振动在无主动抑振时呈负指数衰减，与数学模型对应，在引入PID 控制的三个振动周期后，振动得到了有效抑制，并且维持在一个比较稳定的范围内。

通过图12 和13 可以看出：当引入干扰后，帆板的振动状态发生了改变。而这两种干扰状态下PID的控制参数都是相同的，但是从图中可以看出，相同的PID 控制参数对于两种不同的干扰，仍然具有良好的抑振效果。

如图14所示，为自由振动情况下对有无主动控制的波形的快速傅里叶变换（以下简称FFT（Fast Fourier Transform），从图中可以看到，对于在共振频率下的振动抑制较为明显，这说明在基于MFC 的主动抑振过程中，MFC 的抑振是给帆板一个相同频率的反作用力来达到抑制振动的目的，帆板的固有频率是需要实验和仿真测得的，也是前期建立数学模型和实验的必要参数。

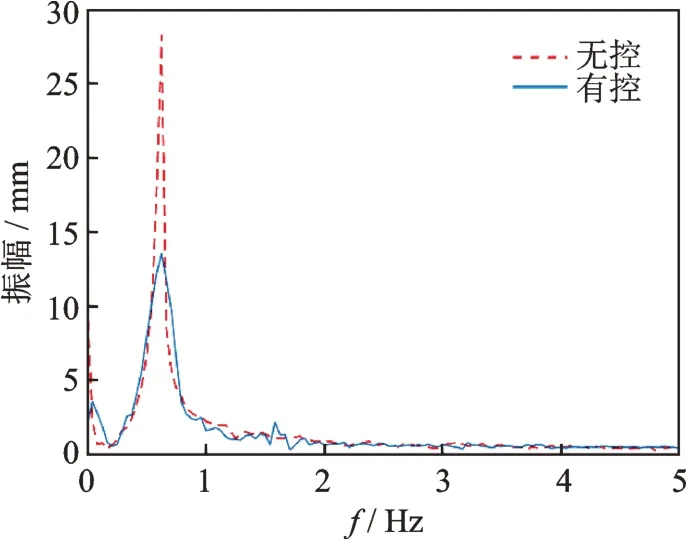
图14 自由振动情况下的FFTFig.14 FFT in free vibration

类似地，在引入干扰的情况下，图15所示为正弦波干扰输入时，有无主动控制的FFT 变换波形对比；图16所示为白噪声干扰输入时，有无主动控制的FFT 波形对比，从图中可以观察到，不同干扰输入的情况下，主动控制的效果是类似的，都能对基频附近的振幅有较明显的抑制作用。

图15 正弦波干扰输入情况下的FFTFig.15 FFT in the case of sinusoidal interference input

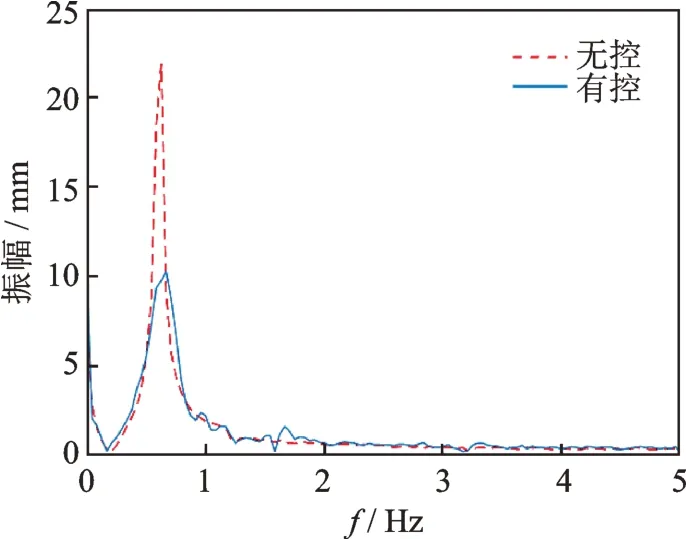
图16 白噪声干扰输入情况下的FFTFig.16 FFT in the case of white noise interference input

实验中提供的干扰信号是自然界中普遍存在的，在现有实验条件下，干扰激励的MFC 为M-4312-P1 型，此MFC 提供的最大输出力为120 N，要比M-5628-P1 型MFC 的最大输出力340 N 要小，这也就是在引入干扰后振动幅值有所下降的原因。

3 结论

本文设计了一套基于压电纤维复合材料MFC 的太阳电池阵帆板主动抑振系统，该系统基于MFC的逆压电效应在MFC上加载电压，使其产生驱动力用于抑制帆板的振动。开展了基于MFC的抑振机理分析，推导了电池阵帆板的振动模型。在此基础上，采用高性能的PID 控制算法，实现了电池阵帆板的主动抑振。通过对比自由振动以及正弦和白噪声两种干扰信号激励下的自激振动，详细研究了主动抑振实验中抑振稳定时间和抑振稳定振幅两项重要指标，最终结论如下。

（1）通过建立MFC 的压电效应方程和理论推导，验证了MFC 作为致动器和传感器的可行性。采用两种规格的MFC 分别作为致动器和传感器，基于应变能最大理论，获到了MFC 的最佳粘贴位置，得到的控制效果更好。

（2）将PID 自整定的控制算法应用于帆板的振动主动控制中，提高了系统开发效率，减小了控制算法对帆板模型的依赖。由于帆板柔度较大，振动频率较低，PID 自整定的响应速度能够满足振动抑制的需求。在太空环境中，PID 自整定具有良好的自我调节能力，能够有效防止驱动器失控的情况发生。

（3）本文设计的系统能够有效地降低基频附近的振动，并且在各种外部输入扰动的情况下，依然能有效地抑制帆板的振动。在自由振动和各种干扰输入的情况下，引入控制后都能在3～5 s 内进入到平衡状态，振动抑制偏差小于3 mm，抑振效率可达4倍以上，抑振效果显著，达到了预期的效果。