基于能量分割的空间域图像融合算法研究

王新赛，冯小二，李明明

基于能量分割的空间域图像融合算法研究

王新赛，冯小二，李明明

（陆军炮兵防空兵学院（郑州校区），河南 郑州 450052）

针对空间域图像融合存在不同图源差异性信息提取、融合权重选取困难等问题，提出了一种新的空间域图像融合算法。利用矩阵相似的基本原理，对红外图像矩阵进行对角化变换，计算可见光图像矩阵在主要特征向量上的映射，采用加权融合的方法处理特征值矩阵，对融合矩阵进行对角化逆变换重构融合图像。实验结果表明，算法在充分保留源图像有效信息的同时，融合图像的整体灰度得到了明显的改善，具有良好的图像质量评估指数和更加优秀的视觉效果。

空间域；对角化；特征向量；图像融合；质量评估

0 引言

随着计算机视觉、图像处理等相关科学技术的快速发展，融合图像因其具备图像信息更加丰富、人眼视觉效果优秀等优点，得到了人们越来越多的重视。图像融合技术是将多传感器采集的数据信息进行处理并再次以图像的形式反映出来的技术，既不是简单的数据叠加，也不可以在融合的过程中引入虚假信息或者产生新的噪声，融合图像能够为下步的人工识别提供更加丰富的数据信息，起到“1＋1＞2”的效果。在光电探测技术中，以可见光探测、红外探测手段发展最为成熟和迅速，在安保、反恐、医疗、军事等众多领域得到了广泛的运用。目前，像素级的图像融合算法可以分为频率域图像融合和空间域图像融合[1-3]。随着小波理论的广泛应用，基于频率域的图像融合算法处理的融合图像效果不断得以改善，但是往往计算繁复、速度较慢，特别是在硬件设备相对简单、处理速度要求高的情况下，往往难以满足工程要求。

传统的空间域图像融合方法的主要优点是计算简单、运行速度快，目前的主流算法有加权平均法[4-5]、IHS（Intensity Hue Saturation）融合[6-7]、PCA（Principal Component Analysis）融合法[8-10]。其中，加权融合算法作为最经典的融合算法，其特点是不对源图像进行任何变换处理，直接对数据进行加权叠加，优点是信息损耗及附加噪声小，在实际工程上得到了广泛的应用。但是，加权融合中源图像的加权因子的选取至关重要，如果加权因子选取不当，甚至会模糊图像已有的边缘、纹理等重要信息；IHS融合、PCA融合算法主要是针对全彩色图像或多光谱（3个以上）图像进行融合。主成分分析（PCA）是一种常用的融合准则。使用PCA方法进行图像融合的常用方法有两种：其一是用于高分辨率全色图像与低分辨率多光谱图像的融合；其二是用于同分辨率图像的融合。将PCA应用于近似图像的融合，其中，PCA方法决定了各近似图像融合时的权重，当融合源图像相似时，该方法近似于加权融合算法，其融合效果对图像之间的相似性依赖很大，应用非常受限。从以上分析来看，当前空间域图像融合算法主要存在2个难点：①很难有效地对源图像的边缘、纹理信息进行分割和提取；②难以找到通用的不同信息的融合规则，导致融合图像的连续性不强。针对以上问题，本文提出一种基于相似矩阵的空间域图像融合算法，利用相似矩阵的基本原理，提取不同图像之间的主要“能量信息”，实现图像的有效融合。实验结果表明，相比传统的空间域融合算法，本文算法具有较好的图像质量评估指数。

1 基本原理

根据矩阵相似的基本定理[11-12]，若输入图像(,)是×大小的一个阶方阵，且可逆，必须存在对角阵，使得：

根据特征值与特征向量的定义可知：

(,)p＝ p(2)

式(2)表明，在几何上，特征向量的方位，经过线性变换后保持不变；在图像处理中，特征值就表示了图像的能量分布。如果对中进行调整，可以通过式(1)实现图像重构。

图1表现了对红外源图像进行对角化分解后的特征值分布及重构图，源图像大小为256×256，特征值数量为256个。图1(a)～(b)分别是红外原始图像以及特征值分布图，从图(b)可以看出，特征值主要集中在一个较小的区间内，经过计算，前50个特征值占全体特征值模值的88.14%，代表了图像的“主要能量”信息。图1(c)～(e)分别是对特征值进行提取后，通过式(1)进行重构后的图像，其与原图像的信息熵比值分别为：70.89%、92.18%、100%。从以上数据可以看出，通过矩阵对角化以后提取的主要特征值能够很好地重现源图像，如果采用全部特征值，则能够完全重构源图像。图像经过对角化分解后得到的特征值表征了图像的一种“能量分布”，特征值表征了能量的大小，特征向量表征为能量的方向性。图像矩阵对角化本质是实现了对图像的“能量分割”，即主要特征值表征了主要信息，包含了图像的主要灰度信息；次要特征值表征了细节信息，包含了图像的细微变化。

2 基于能量分割的融合算法

本文提出的算法流程图如图2（以红外原理图像为基准图像）所示。其基本流程是：

步骤1：根据不同源图像的特点以及不同的融合要求，选定基准图像并进行矩阵的对角化。

步骤2：从对角化矩阵结果中，提取基准图像的特征值矩阵、特征向量矩阵；

步骤3：将另一幅源图像在提取的特征向量矩阵上进行映射，得到主要能量特征值矩阵和差值图像；

步骤4：对待融合图像的特征值矩阵进行融合并重构主成分图像；

步骤5：对主成分图像和差值图像进行融合，得到最终融合图像。

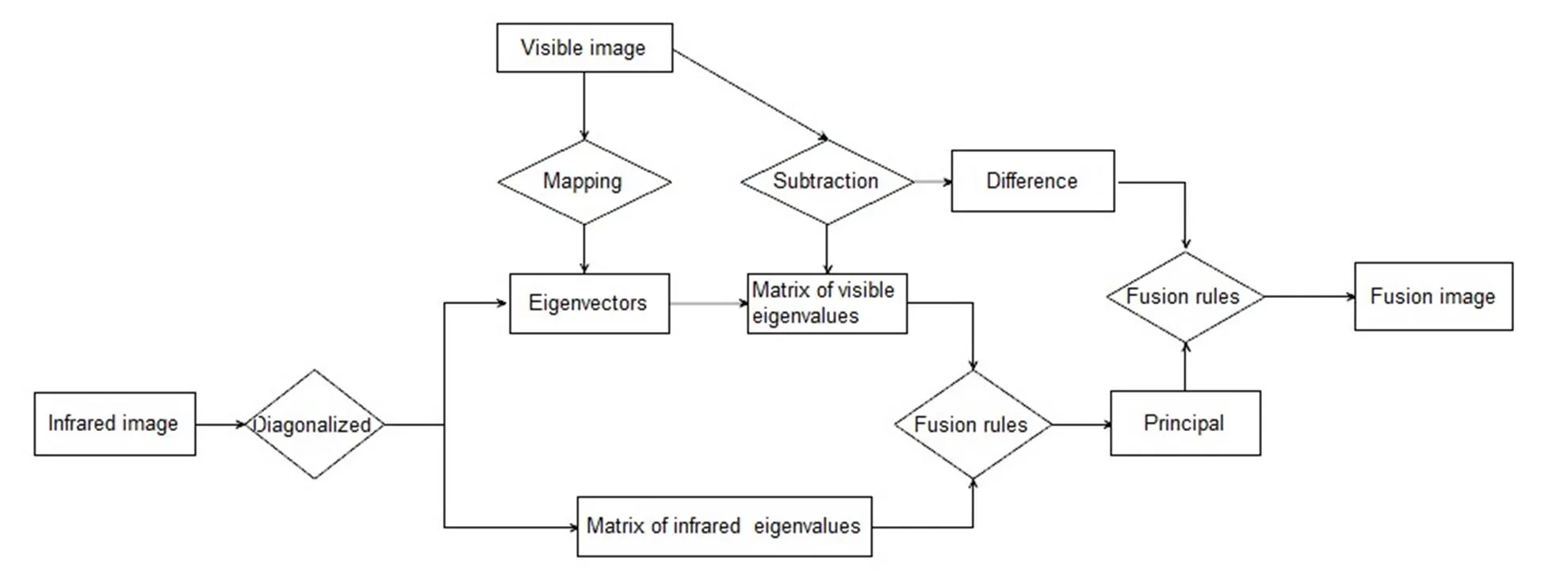
图2 本文算法流程图

2.1 基准图像矩阵的对角化

设v(,)和i(,)分别为图像配准过的可见光和红外图像。随着光学器件的不断发展，可见光图像往往要比红外图像具有更好的图像分辨率和更清晰的细节。因此，通常采用红外图像i(,)作为基准图像，进行对角化分解：

i(,)＝iii－1(3)

得到特征向量矩阵i、特征值对角阵i。

2.2 基于基准图像特征向量的映射

为了寻找可见光图像与红外图像之间的“相似性”特征，因此可以计算可见光原始图像v(,)在红外图像特征向量矩阵i上的映射。

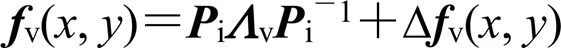
式中：ivi－1和Dv(,)分别表示为可见光图像的主要特征信息和细节信息。根据式(4)，v为计算v(,)对于特征向量i的最大映射分量，通过式(5)可将式(4)转化为求v(,)的极小值问题。

式中：i表示为对应于特征向量i的最大映射值，其中i表示红外图像的第个特征向量。从而完成对可见光图像“能量分割”过程，因为采用了同样的变换坐标系，保证两者具有同样的能量特性，实现了对不同能量间的图像融合。Dv(,)是关于i的函数。

可以根据源图像的特点以及对融合图像质量的要求，设置不同的函数类型得到不同的映射值。比如，可以选择信息熵IE（Information Entropy）、标准差STD（Standard Deviation）、平均灰度AG（Average Grayscale）等图像质量评估指标来构建Dv(,)函数。本文以平均灰度为例，对v进行求解：将式(5)展开：

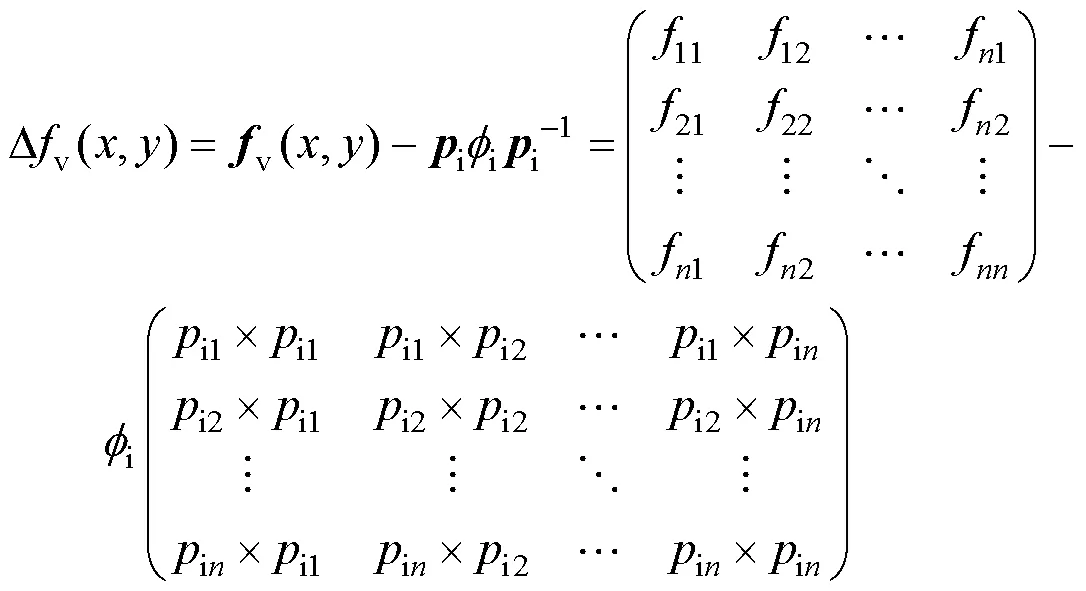
式中：in表示特征向量i的第个元素。

则Dv(,)为关于i的一元一次方程，根据平均灰度的定义：

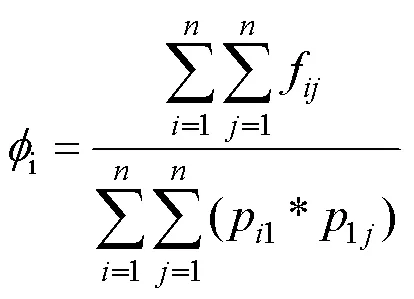
依此类推，得出映射矩阵：

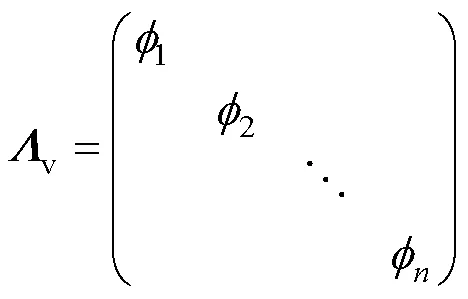
2.3 融合特征值

由于特征值反应了原始图像的概貌，图像均匀而平滑，所以较适合采用系数加权的方法对其进行加权融合。i和v分别为红外图像Di(,)和可见光图像Dv(,)的特征值矩阵，为融合系数，则：

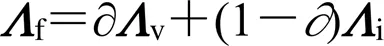
式中：f为融合后的特征值矩阵。关于融合系数的选择与经典的图像加权方法相似，通常取＝0.5，即采用加权平均的方法，也可根据图像特征进行选取，比如对图像的整合亮度要求较高，可采用：

2.4 融合图像重构

根据式(1)进行主成分图像重构，即：

得到最终融合图像：

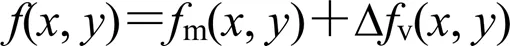
3 实验结果与分析

为了验证本文算法的有效性，选取了2组红外图像与可见光图像，经典的camp系列图像和tree系列图像。本文采用的对比算法有2种，分别为PCA分析法、加权融合方法，融合结果分别如图3和图4所示，本文选用信息熵IE、平均灰度Mean、平均梯度AG（Average gradient）作为图像质量评估指标，表1为图3和图4中相关图像的质量评估结果。

图3 Camp系列图像的融合结果

图4 tree系列图像的融合结果

表1 不同算法客观评估指标值

从表1可以看出，camp系列图像和tree系数图像的主要区别在：camp系列图像的可见光图像和红外图像的信息熵、均值和平均梯度比较相近，其差异性要远小于tree系列图像。从视觉效果上说，camp系列图像的对比度较强，可见光图像和红外图像的纹理、边缘比较清晰，可见光图像中无法看到人物信息；tree系列图像的整体灰度相对平均，纹理、边缘相对模糊，可见光图像和红外图像均可看到人物信息。从3种融合图像的效果来看，相对比经典的加权平均法、PCA融合算法，本文所提算法得出的融合图像在信息熵、均值上和平均梯度上均有所提高，特别是图像的整体灰度得到了明显的改善。从视觉效果上来看，本文所提算法得出的融合图像有效保留了源图像的边缘、细节信息，整体亮度得到了明显的提升。

4 结语

本文提出了一种基于相似矩阵的空间域融合算法，在空间域对主要成分进行了加权融合，提取了可见光图像与红外图像间的“差值”图像，即细节成分，与主要成分进行了图像融合。实现结果表明，相对于经典的加权融合法、PCA分析法，本文算法能够在空间域有效地实现可见光和红外图像融合，融合图像的相关信息得到了增强，具有良好的融合效果。但是该算法在实际运用过程中广泛的非方阵格式图像，由于无法进行对角化分解，可以采用人工分割图像等方法手段进行融合，有待进一步研究完善。

[1] 甄媚. 可见光图像与红外图像融合算法研究[D]. 西安: 西安科技大学, 2019.

ZHEN Mei. Research on visible image and infrared image fusion algorithm[D]. Xi'an: Xi'an University of Science and Technology, 2019.

[2] 周渝人. 红外与可见光图像融合算法研究[D]. 长春: 中国科学院研究生院(长春光学精密机械与物理研究所), 2014.

ZHOU Yuren. Research on infrared and visible light image fusion algorithm[D]. Changchun: Graduate School of Chinese Academy of Sciences (Changchun Institute of Optics, Fine Mechanics and Physics), 2014.

[3] LI Hui, QI Xianbiao, XIE Wuyuan. Fast infrared and visible image fusion with structural decomposition[J]., 2020, 204: 106182.

[4] 赵娟, 孙澎涛, 吴粉侠, 等. 基于像素级的图像融合[J]. 长春工程学院学报: 自然科学版, 2011, 12(2): 106-108, 112.

ZHAO Juan, SUN Pengtao, WU Fenxia, et al.Pixel-level image fusion[J].: Natural Science Edition, 2011, 12(2): 106-108, 112.

[5] 曲杨, 许卫东, 杨骏堂, 等. 一种可见光和红外图像加权融合最佳权值因子的确定方法[J]. 电子世界, 2017(13): 12-14.

QU Yang, XU Weidong, YANG Juntang, et al. A method for determining the optimal weight factor for the weighted fusion of visible and infrared images[J]., 2017(13): 12-14.

[6] 刘成云, 常发亮, 刘春生, 等. 区域特征动态加权的IHS小波遥感图像融合[J]. 计算机工程, 2012, 38(8): 198-200.

LIU Chengyun, CHANG Faliang, LIU Chunsheng, et al.Fusion of IHS wavelet remote sensing images dynamically weighted by regional features[J]., 2012, 38(8): 198-200.

[7] TU Teming, SU Shunchi, SHYU Hsuen Chyun. A New Look at HIS-like Image Fusion Methods[J]., 2001, 2(3): 177-186.

[8] Rajenda Pandit Desale, Sarita V Verma. Study and analysis of PCA, DCT & DWT based image fusion techniques[C]//, 2013: 1-4.

[9] 潘梅森, 汤井田, 杨晓利. 采用PCA和PSNR的医学图像配准[J]. 红外与激光工程, 2011, 40(2): 355-364.

PAN Meisun, TANG Jingtian, YANG Xiaoli. Medical image registration using PCA and PSNR[J]., 2011, 40(2): 355-364.

[10] 吴粉侠, 李红, 李洪星. 基于NSCT变换和PCA的图像融合算法[J].航空计算技术, 2015, 45(3): 47-51.

WU Fenxia, LI Hong, LI Hongxing. Image fusion algorithm based on NSCT transform and PCA[J]., 2015, 45(3): 47-51.

[11] 周琴. 矩阵特征值和特征向量在实际中的应用及其实现[J]. 高师理科学刊, 2019, 39(7): 8-10.

ZHOU Qin. Application of matrix eigenvalues and eigenvectors in practice and their implementation[J]., 2019, 39(7): 8-10.

[12] 闵超. 关于矩阵特征值有关性质的探讨——线性代数教学思考[J]. 教育教学论坛, 2019(24): 190-191.

MIN Chao. Discussion on the properties of matrix eigenvalues -linear algebra teaching thinking [J]., 2019(24): 190-191.

Research on Spatial Domain Image Fusion Algorithm Based on Energy Segmentation

WANG Xinsai，FENG Xiao’er，LI Mingming

(Army Academy of Artillery and Air Defense Force Zhengzhou Campus, Zhengzhou 450052, China)

To address the problems of image fusion in the spatial domain, such as the extraction of different image sources, and challenges in selecting fusion weights, a new spatial-domain image-fusion algorithm is proposed. Using the basic principle of matrix similarity, the infrared image matrix is diagonally transformed and the visible light image matrix is mapped onto the main eigenvectors. Then, the weighted fusion method is used to process the eigenvalue matrix and the fusion matrix is diagonalized as an inverse-transformed and reconstructed fusion image. The experimental results show that the algorithm fully retains the effective information of the source image; moreover, the overall grayscale of the fused image is significantly improved. Thus, the algorithm offers a strong image quality evaluation index and better visual effects.

spatial domain, diagonalization, feature vector, image fusion, quality evaluation

TP391.41

A

1001-8891(2022)07-0726-06

2020-08-24；

2020-09-28.

王新赛（1963-），男，江苏睢宁人，教授，博士，研究方向为光电成像、模式识别。E-mail:wangxsai@126.com