加工中心孔系加工的编程技巧
2022-07-26王健,陈琳
王 健,陈 琳
(佛山市技师学院,广东佛山 528237)
1 研究背景与意义
孔系在端盖、法兰、箱体、通用夹具等零件中是非常常见的,传统的加工方法是利用钻模在普通钻床上加工,但这种加工方法工人劳动强度大、工序分散效率相对较低、孔的相对位置误差也较大。随着数控机床的不断普及,由于其对工人的劳动强度低、工序集中、效率高、操作方便灵活的特点,越来越多的孔系零件被安排在数控机床上加工。但普通加工程序数据繁杂,要怎样对数控加工程序进行简化,避免计算错误,且易于修改,才能完成孔系的加工。
2 固定循环指令的基本概念
以FANUC为例的钻孔循环指令(见表1)。
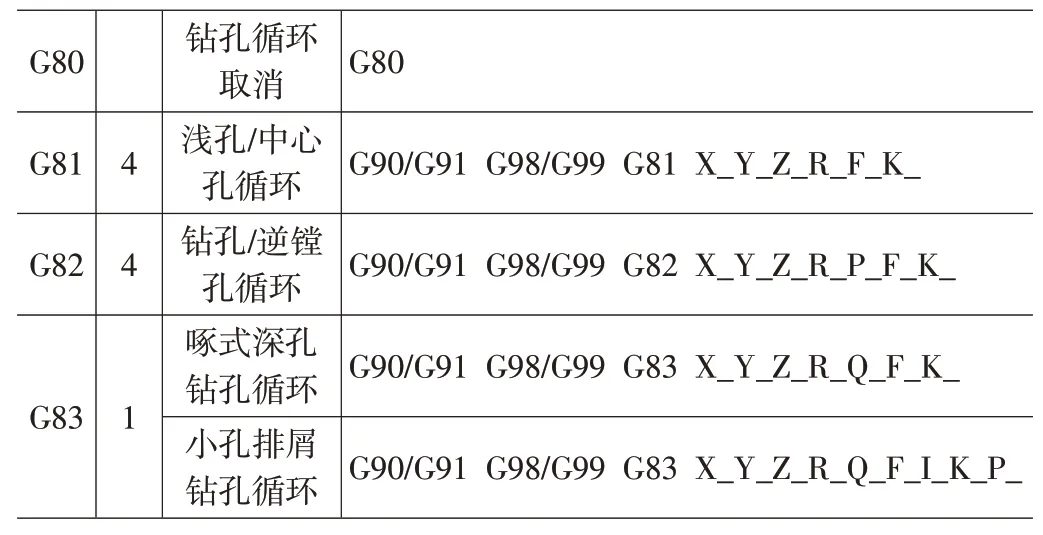
表1 FANUC为例的钻孔循环指令
在数控加工中,孔加工的动作循环基本已经标准化。一般动作可分为:孔位置定位、快速移至R面、工进加工和快速退回等,如图1 所示。系统将这样一系列的加工动作预先编好程序存储在系统中,再通过孔加工循环代码调用实现简化编程工作。这样的动作循环G代码称为循环指令。
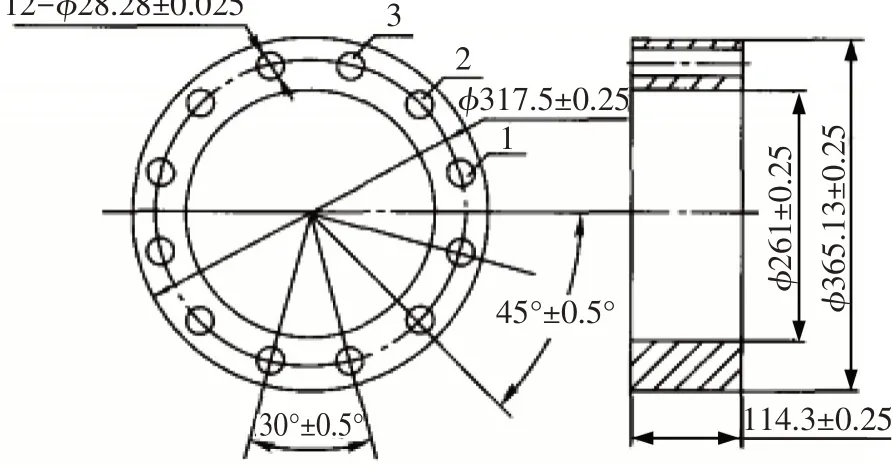
图1 盘类零件
以FANUC系统钻孔循环为例格式如下:
G98(G99)G90(G91)G_X_Y_Z_R_F_Q_K_
参数说明:
(1)X、Y为加工孔位置坐标。
(2)Z为孔底坐标,G90时Z为孔底坐标,G91时Z为R点位置到孔底的距离(一般为负值)。
(3)R为安全平面位置。G90 时为R面的坐标位置,G91时为初始点到R面的距离(一般为负值)。
(4)F为钻孔切削进给速度。
(5)当G83时Q为每次进给深度。
(6)K为钻孔重复次数。
3 研究的主要内容与方法
本文主要研究的主要内容是在传统的圆周、矩形阵列孔系加工编程中,程序繁多、数据计算量大、数值复杂等问题,导致加工中容易出错引发事故;通过运用增量编程、宏程序编程、子程序编程、极坐标编程的多种方法简化程序,以具体的编程过程来对比论证该方法的简洁实用性。
4 圆周孔系的编程方法
圆周孔系是指按一定规律分布在圆周上的一系列的孔,若孔的尺寸相同,则使用孔的固定循环指令也相同,不同的是每一个孔的位置不同。同一个孔工序的不同(如钻中心孔、钻孔、攻螺纹等)只需更换刀具和循环指令即可。所以,编程时的关键和难点在于如何确定孔的位置。
4.1 传统坐标编程法
坐标编程法是指通过数学计算的方式计算出加工孔的位置坐标值,再将所计算的位置坐标值等数据编入钻孔循环程序段中,运行该程序,钻孔即可完成。使用这种方法计算量较大,数据繁琐且容易计算错误,程序段多,在系统中输入程序时,由于数据及数据的小数位较多,极易造成输入错误,从而导致零件加工报废甚至损坏机床。
编程过程如下:根据图1所示零件计算得出孔1、2、3的中心坐标并编程:
孔1:(X153.341,Y41.088)。
孔2:(X112.253,Y112.253)。
孔3:(X41.088,Y153.341)。
根据计算坐标数据编程如下:
………
G0 X153.341 Y41.088 (定位至孔1)
G98 G90 G83 X153.341 Y41.088 Z-120. R10.Q5. F100.(加工孔1)
X112.253 Y112.253 (定位并加工孔2)
X41.088 Y153.341 (定位并加工孔3)
………
由上述程序段可以看出,如要完成圆周12个孔的钻孔加工,至少需要12个以上的钻孔程序段,程序数据复杂,空位置数值小数多,容易出错。这种编程方法在有规律的孔系中显得笨拙,但在没有规律的孔系中只能选择这种编程方法。而且使用这种绝对定位的方式不会产生累积误差,孔的定位精度较高。
4.2 宏程序与极坐标结合编程法
宏程序可以运用变量进行编程,在程序中可以对变量进行赋值,同时变量之间还可以进行算术与逻辑运算,改变执行顺序。
极坐标可将一般的直角坐标位置转变为半径和角度表达,减少了对圆周孔系的位置计算。
宏程序的变量及变量引用、变量运算:
变量表示方法(FANUC 为例):一个变量由“#”和变量序号组成,如#1、#2、#101、等。#1-#99 为局部变量,#100-#999为公共变量,#1000以上为系统变量。
变量引用:将地址附后的数值用变量来代替的方法称为变量引用。如:X#1 Y#2 F#5等。
变量运算:变量之间可进行数学运算和逻辑运算,运算的次序依次为函数运算(SIN、ASIN、COS等)、乘和除运算(*、/、AND 等)、加和减运算(+、-、OR等)。如:#1=#2-#3*SIN[#4]。
条件表达式:
格式:IF[(条件表达式)] GOTOn ;
如:IF[#10 GT 0] GOTO 2;表示如果表达式条件满足时,将转移到N2的程序段。如果条件不满足,将执行下一个程序段。
极坐标指令格式
G16 X Y (开启极坐标编程)
G15(取消极坐标编程)
X为圆弧半径值
Y为角度值
如图2 中的零件,可以通过极坐标的转换确定每个孔的中心位置,简化了计算工作,再使用变量简化程序。现以FANUC系统为例,编写图1零件的圆周孔系加工程序。
O0001 程序名
N10 G90 G54 G0 Z100; 程序开始
N20 M3 S250 M8; 主轴正转、转速250r/min、冷却液开
N30 #1=15; 初始角度赋值#1变量15°
N40 #2=30; 角度增量赋值#2变量30°
N50 #3=158.75;圆周孔系所在的圆弧半径值
N60 G0 G16 X#3 Y#1; 启用极坐标编程,定位至孔位置
N70 G98 G83 Z-120. R5. Q5. F100;开始钻孔循环
N80 #1=[#1+#2]; 更新角度变量
N90 IF[#1 LE 360] GOTO 60; 条件判断
N100 G15 G90 G80 G0 Z100; 取消极坐标编程、抬刀
N110 M30;
由上述程序可见,用宏程序和极坐标编程,省略了计算过程,避免了计算产生的错误,程序简洁,一个完整的程序也只有11个程序段,前5段为程序头及变量赋值,程序的长短与孔的个数无关。通用性强。如要加工不同圆周、不同数量或不同深度的孔系,都只需改变相应的变量赋值就可以,不需修改程序,可作为企业不同系列圆周孔系的很好模板。
4.3 增量方式与极坐标结合编程法
固定循环的增量方式编程是指以增量的形式对固定循环中的数值进行指定,对相对位置固定的孔系加工编程应用相当方便,只需在一个循环指令中指定相对的位置及重复的次数即可,再与极坐标相结合完成圆周孔系的编程。
增量方式在固定循环中的应用(FANUC为例):
G98(G99) G91 G83 X_Y_Z_R_Q_K_F_;
参数说明:
G91:增量方式
G83:钻孔固定循环
X、Y:G91时为当前位置到加工孔的距离
Z:G91 时Z为R点位置到孔底的距离(一般为负值)。
R:为安全平面位置。G90 时为R面的坐标位置,G91时为初始点到R面的距离(一般为负值)。
F:为钻孔切削进给速度。
Q:当G83时Q为每次进给深度。
K:为钻孔重复次数。
如图2 所示零件,同样使用极坐标的方式确定加工孔的位置坐标,再使用增量的方式简化加工程序段。以FANUC为例编写图2加工程序:
O0001 程序名
G90 G54 G0 Z100; 程序开始
M3 S250 M8; 主轴正转、转速250r/min、冷却液开
G16 G98 G83 X158.75. Y15. Z- 120. R5.Q5. F100;启用极坐标方式,定位并加工出孔1。
G98 G91 G83 Y30. Z- 125. R- 95.Q5 K11 F100;启用增量方式,角度增量30°,重复11次,加工余下11个孔。
G15 G90 G80;
M30;
由上述程序可以看出,使用增量方式与极坐标结合的方法,相对于上一种方法更为简洁,免去了计算过程同时还大大减少了程序段,修改与较为方便,只需改变增量的大小和重复次数即可。
5 矩形阵列孔系的编程方法
加工中心上经常会遇到如图2所示的矩形孔系零件,这些孔呈一定规律排列,要对此类孔系零件进行加工,利用手工编程程序段相对复杂、繁多,在输入时容易出错。下面以FANUC系统为例对矩形阵列孔系进行编程,充分利用子程序、宏功能等,对复杂的手工编程进行简化,体现程序的简洁性和准确性。

图2 矩形孔系零件
5.1 传统坐标编程法
传统坐标编程法通过每一个加工孔坐标输入到孔加工程序中,运行程序加工出所需孔,在孔较多的孔系零件中,这种编程方法数据量非常大,程序段多,在输入时耗费时间及容易出现输入错误,从而发生浪费或事故。根据图3所示零件各孔位置尺寸计算坐标并编程:
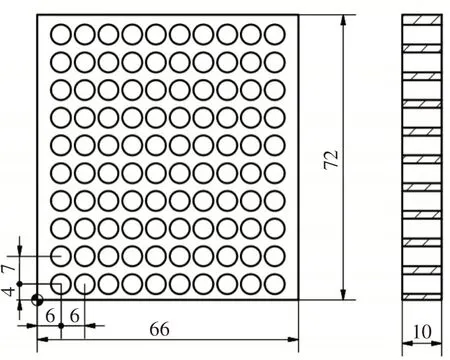
图3 矩形孔系零件
(以零件左下角作为原点)
O0001
G90 G54 G0 Z100;
M3 S700;
G83 X6 Y4 Z-15 R5 Q2 F100;
X12;
X18;
X24;
………
X6 Y11;
Y18;
Y25;
………
G80 G0 Z100;
M30;
由上述程序可以看出,传统的坐标编程法在孔较多的孔系中显得笨拙,上图100个孔完全使用传统坐标编程的话程序段至少需要100段以上,而且需要计算各孔的位置坐标,但在没有规律排列及较少的孔加工中应用相对方便,且能保证较高的位置精度。
5.2 子程序宏功能增量方式结合的编程方法
根据图3 零件所示,所有加工孔的结构尺寸都相同,不同的只是所加工孔的位置,若将孔加工循环的程序以增量的形式编写成子程序,再用宏功能重复调用孔加工的子程序,这样不但编程简单方便,而且不易出错,也大大简化了程序,在日常生产中使用非常方便。
以FANUC系统为例子程序功能介绍:
当加工程序需要多次运行一段同样的轨迹时,可将这段轨迹编成子程序存储在机床的程序存储器中,每次在程序中需要执行这段轨迹时便可以调用该子程序。
子程序格式:
O×××× 子程序名
………;
………; 程序内容
M99; 返回主程序
在主程序中,调用子程序的格式:
M98 P×××××;
M98为调用指令,地址P后面的数字中,后四位为调用的子程序的程序名,前面几位则为调用的重复次数(调用一次不用指定),例如:
M98 P51001; 调用1001号子程序,调用5次。
M98 P1001; 调用1001号子程序,调用1次。
宏功能及增量方式在圆周孔系中以有相应介绍,在此不再作相应解释。
下面就以图3零件为例,使用子程序、宏功能及增量方式相结合的方法进行孔加工程序的编程:
O0002 主程序名
N10 G90 G54 G0 Z100; 程序开始
N20 M3 S700 M8; 主轴正转,转速700r/min,冷却液开
N30 #1=6; 初始变量赋值
N40 #2=4; 初始变量赋值
N50 #3=7; 孔位增量变量赋值
N60 G98 G83 X#1 Y#2 Z-15. R5 Q2 F100;定位并加工第一个孔
N70 M98 P1001; 调用子程序,调用1次
N80 #2=[#2+#3]; 更新变量,加工下一排孔
N90 IF[#2 LE 70] GOTO 60; 条件判断
N100 G90 G80 G0 Z100; 抬刀
N110 M30; 程序结束
O1001; 子程序名
G98 G91 G83 X6. Z-20. R-95. Q2 K9 F100.;
增量方式加工循环,重复9次加工出一排余下9个孔
G90 G0 Z100; 抬刀
M99; 返回主程序
由上述程序看出,通过子程序、宏功能及增量方式相结合的编程方法大大减小了程序的复杂性,简化了程序,100 个孔一条完整的程序也才只有十多段程序,避免了孔位计算减小了劳动强度。
6 结论
通过上述各种编程方法的比较,传统坐标编程比较原始,计算量较大容易出错,但在没有规律排列的孔系中,是唯一的方法,孔的相对位置精度容易保证;在圆周孔系中使用极坐标简化了孔位置的计算,使用宏功能及增量方式减少了程序量,适应不同直径圆周分布、不同数量的孔加工;矩形阵列孔系中,使用子程序方式减少了孔坐标的重复输入,增量方式避免了孔位置坐标的计算,使用宏功能简化了程序。对操作工人来说更简单易懂,体现更强大的优越性,不但程序简单,而且计算方便,通用性也很强。
