基于动力参数的桥墩冲刷深度识别方法

姚博川 陈 彦 董政显 卢星宇

（吉林大学交通学院，吉林 长春 130022）

1 概述

河流冲刷是造成桥梁损毁的重要因素，其造成的桥梁坍塌事故在国内外都屡见不鲜。目前，对于桥墩冲刷病害的监测主要通过潜水观测、声呐探测等方式实现[1]，存在人力物力成本较高的问题，且在洪水等极端条件下不易实施。而理论计算主要是借助河流流速、河床深度等水文条件，利用经验公式进行预估[2]，往往会产生较大的误差。可见，现有的桥墩冲刷深度监测方案在工程应用上还存在进步的空间。

据此，以湖南省沅江白沙大桥为例，提出一种基于动力参数的桥墩基础冲刷深度的识别方法，构建损伤识别指标对冲刷工况进行预测。借助桥梁的有限元数值模型，只要测出运营状态下的自振频率，就可以对其安全性进行定量的评估。

2 冲刷识别理论方法

2.1 冲刷识别指标的构建

当桥墩基础发生冲刷损伤时，结构整体的刚度下降，导致自振频率也会随之降低，符合参数识别的要求[3]。对于多跨桥梁，当冲刷损伤存在于多个墩柱时，需要考虑桥梁的多阶自振频率。为此，可先将不同的冲刷工况编号区分，并定义对应的频率向量为：

式中：m——冲刷工况的编号;

fn——对冲刷较为敏感的各阶固有频率（Hz）;

由于各阶频率对冲刷损伤有不同的敏感度，对于任意冲刷工况，必有唯一的频率向量F 与之对应。通过有限元软件进行模型分析，可以求出不同工况下的频率向量，借助回归拟合等方法可得到大量的频率向量作为样本。当桥梁测试中得到各阶自振频率后，即获得实测的频率向量Ft，通过与样本中所有的频率向量Fm对比，相似度最大的频率向量对应的工况即为反演工况。相似度可以采用欧氏距离[4]度量，其表达式为：

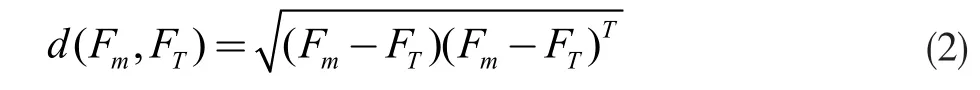
为了减小对冲刷损伤不敏感的振型对识别带来的误差，应当考虑各阶振型的权重，则识别指标可定义为：

式中：Ki——第i 阶振型对应的灵敏度系数，由实桥的几何参数、检测环境等因素综合确定

SEm——实测频率数据对号工况的相似指数

显然，实测频率向量FT对各种样本工况有不同的SE值。由SE 的定义可知，其值越小，表示实测数据与某一样本工况相似程度越高，因此反演工况可取使SE 值最小的样本。

2.2 冲刷反演方法

基于1.1 中提出的相似指数，涉水桥梁的冲刷损伤预估可以按如下步骤进行：

2.2.1 根据桥梁的设计图纸，建立有限元模型。

2.2.2 对模型进行不同冲刷工况下的数值模拟，并利用神经网络算法对数据进行拟合。判断对冲刷敏感的振型，得到各个工况对应的频率向量Fm。

2.2.3 针对敏感振型对桥梁进行模态测试，得到实测的频率向量FT，计算该实测结果对各种不同工况的识别指数SEm，从而确定反演出的冲刷损伤情况。

3 算例分析

3.1 示例桥梁简介

位于国道兴阳线（G234 线）上的湖南省益阳市沅江白沙大桥建成于2002 年，主桥为四跨一联的预应力混凝土连续梁桥（50m+90m+150m+90m），如图1 所示。大桥桥面宽度为13m，横截面布置采用C50 双悬臂矩形单箱单室的变高度箱型截面。对于下部结构，22、23 号主墩采用高桩承台基础，每墩桩基分三排共13 根D180cm 钻孔灌注桩，桥墩为圆端形实体墩。21、24 号均为两排D180cm的钻孔灌注桩、D250cm 的双柱式圆墩[5]。

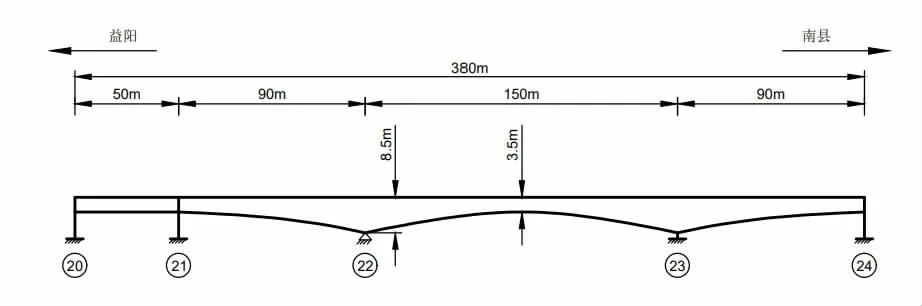
图1 白沙大桥主桥桥墩编号示意图

3.2 有限元模型的建立

为探究桥墩基础受冲刷影响的动力参数变化规律，需要建立实桥的有限元模型。本文使用SAP2000，选取22 号墩为主要冲刷研究对象，建立20 号至24 号墩的四跨有限元分析模型，如图2。

图2 白沙大桥主桥有限元模型

对模型下部结构的刚度，采用分层土模型法，用结点弹簧来模拟桩——土之间的相互作用，忽略摩擦作用（不计竖向弹簧，扭转弹簧，桩底采用固定端约束）。由m法可知，桩基的侧向弹簧分布刚度随深度线性增长[6]，其表达式为：

式中：m——地基系数的比例系数，一般通过现场试验获得，也可以参照规范[7]选取。

b0——桩的计算宽度

z——计算点距局部冲刷线以下的深度

结点弹簧的刚度可由面积叠加法[8]求得，不同程度的冲刷损伤可以通过调整结点弹簧刚度的方式来模拟。

3.3 冲刷规律分析

为了达到预测冲刷损伤的目的，先对未冲刷时桥梁的动力特性进行探究。经过仿真运算，可以得到各阶振型及其对应自振频率，如表1。

表1 未冲刷时模型频率分析结果

通过调整土弹簧刚度来模拟不同的冲刷工况，对模态变化做规律性的分析，即可形成反演各墩冲刷深度的算法。为简化计算，这里以22 号、23 号主墩的冲刷为研究对象，发现各阶频率随冲刷深度的变化体现出一定的相似性，其中纵向二阶振型的变化如图3 所示。

图3 纵向二阶频率随两墩冲刷深度的变化

为区别不同振型对冲刷造成影响的差异，使用灵敏度系数来表征各阶频率对冲刷损伤的敏感性。注意到，冲刷规律可近似拟合为某一二元函数，因此灵敏度系数Ki可定义为：

式中：fi——第i 个振型的自振频率（Hz）；

φ——调整系数，可根据实际情况灵活选取，这里取1000；

Z1——22 号墩冲刷深度（m）；

Z2——23 号墩冲刷深度（m）；

计算各阶振型的灵敏度系数，选取Ki相对较大且模态测试中较易得到的振型组成频率向量中的各项，结果如表2 所示。

表2 灵敏度系数计算结果

3.4 冲刷损伤的识别

在确定灵敏度系数Ki的具体形式后，利用桥梁的模态测试结果即可进行相似指数SE 的计算，反演的冲刷损伤即为SE 值最小时的对应工况。

为检验该识别方法的准确性，可以先预设冲刷工况，通过有限元数值模型进行模态分析，将得到的各阶频率进行反演，比较反演工况与预设工况是否吻合。例如，模型桥梁在22 号墩冲刷4m、23 号墩冲刷3m 时，其纵向二阶频率、横向一阶频率和横向二阶频率分别为1.6926Hz、0.9296Hz、1.1535Hz，按照本文的方法进行反演，得到的冲刷深度分别为3.990m 和2.997m。对其他工况进行相同的验证，吻合度均良好，误差均未超过0.1m，具体结果如表3 所示。

表3 反演程序计算结果

4 结论

4.1 本文提出一种基于动力参数的桥墩冲刷深度识别的方法，将冲刷深度监测与动力特性定量地联系在一起，是一种较为新颖的间接监测方案。

4.2 以湖南沅江白沙大桥为示例结构，建立了主桥的有限元模型，并对其在不同冲刷工况下的动力参数进行了分析，确立相似指数 为本方法中的识别指标。

4.3 利用回归分析法，得出自振频率与桥墩冲刷深度的定量关系。

4.4 在对桥梁进行模态测试后，可利用实测数据对桥墩冲刷进行反演，从而确定各墩的损伤情况。

4.5 实际工程中由于桥梁构造各不相同，自振频率随冲刷深度的变化情况可能略有差异，而支座硬化、桩体结构性损伤也会对振动特性产生影响。如何综合考虑多种损伤情况下桥梁结构功能的评定，是下一步有待研究的问题。