弱侧限条件下沉井纠偏及挠度控制研究

聂 鹏 孙春辉 耿志华 马 勇 卢国营

（中电建路桥集团有限公司,北京 100048）

在各大构筑物施工中沉井施工法受到较多关注，但沉井涉及地下半地下作业，对地下空间的物理性质的描述是制约沉井技术的一个难题。这一问题，暴露出工程领域对于沉井作业前，土体本身的性质研究严重不足。因此，从土体的侧限条件分析，把沉井下沉的偏位和挠度问题放在土体性质受力的范畴内研究；从而为沉井工程做好理论分析基础和技术支撑。

1 沉井概况

沉井施工中最怕遭遇淤泥质土体，因其侧限条件差，沉井在下沉就位中，其侧向控制不足，极有可能产生横向位移，导致沉井整体偏位以及发生侧向挠度[1]。如不及时纠正，沉井将会失败或对沉井结构面造成失效。沉井下沉要求是在下沉过程中既不过快也不能过慢，保持匀速破土下沉，及时到达下沉指定位置。

弱侧限控制下，沉井对土体的压力近似构成土体的三向运动，即土体处于三轴受力状态之下。在这种状态下，沉井会受到微弱侧向压力影响，对于沉井轴线带来一定偏位，称其为弱侧限。通常沉井均在完全侧限条件下进行，而在弱侧限条件下的沉井技术要求高，难度相对大，需要更精确的沉井力和土体状态的准确把握，方能在实际工程中取得相应效果。

2 沉井下沉破坏机理分析

2.1 沉井破坏形式及过程

沉井发生破坏其主要是由土体运动，发生管涌，其机理为土体渗流[2]。图1 为沉井下沉过程中土体运动变化导致沉井破坏。图中为沉井受力方向。

图1 沉井下沉土体运动破坏过程

在沉井工作开始后，传力机制是透过沉井井壁向下传递荷载，而后由井壁下端传递给土层。土体在受到荷载后，将改变原有的土体秩序，发生扰动，这种扰动不断积蓄，会带来沉井底部隆起；同时隆起侧底端形成塑性区。塑性区部分不会参与土体与沉井之间的相对传力和相对运动[3]；而当沉井接长，继续下沉，土体进一步受到向下的压力，沉井内一侧由于隆起超过限度发生管涌，即大面积散状土体开始呈规律性流动；继续发展，土体大量管涌，而要维持相对平衡，则原有位置土层开始向下沉陷，管涌此时达到最大规模。

2.2 土体弱侧限条件状态分析

土体侧限条件是沉井工程需要了解的一项工程参数。对于实验室常规环刀法进行有侧限的土体强度分析并不能适用在工程实际环境中的土体情况。真实三维空间中，土体受到三向压力，处在弱侧限的环境中[4]。因此对于沉井的侧限条件的分析，直接影响沉井纠偏与挠度控制。

取某工程现场施工土体，取土位置为所在沉井向下4-5m 的土体芯样，其基本土性参数值如表1 所示。

表1 土体芯样基本参数

在此芯样上进行土体弱侧限试验。由于现场沉井分为四次接高进行，因此将现场每节井壁的实际荷载值进行平均化处理，分别模拟测试4 次下沉状态下，土体芯样的抗剪强度。根据简化计算，从起沉开始，共分为4 次下沉，沉井井壁接高3 次，将土体4 次沉井结果进行分析整体，得到图2 芯样抗剪强度分布值。

图2 土体芯样在井壁压力作用下的抗剪强度分布

由图2 可知：所有4 节井壁都呈现一个变化规律，在沉井初期，由于受荷载较小，其抗剪强度值也相应较小；随着压力值不断加大，抗剪强度也随之变大。此外，由于井壁是一节一节不断接高下沉，因此首节井壁的抗剪强度表现为最小，其后井节呈递增趋势。

3 土体固结度分析

3.1 沉井附加应力

沉井工程对于土体的扰动很大，在处于静止状态的土体中进行沉井。会带来沉井的附加应力，附加应力的研究在工程界及学术研究中论断很多，至今仍沿用的计算基础为法国数学家J. Boussinesq[5]于1885 年提出的半无限均质弹性体在一个集中力P 作用下，弹性体内部产生的应力分布理论。其解法为弹性理论解，也称布辛内斯克理论解。该解法给出了任意弹性体内部六个应力值和3 个方向的位移值。针对本文所要研究沉井的附加应力，可以近似假定为满足布辛内斯克理论解，则有：

式中，σz为所求附加应力；R 为所求点距离原点的距离；对于R 的求解，对沉井与土体接触点几何中心建立向下的空间直角坐标系（如图3 所示），从而由坐标系内距离公式可以解出沉井下任一位置处的R 值大小，公式如下：

式中，x、y、z 为土体中任意点M 在沉井开始下沉的任意时刻的空间坐标值；r 为任意点M 在平面的投影距离。图2 给出了沉井模型，根据布辛内斯克弹性理论，可以将土体中质点M 进行微元体应力状态分析，所求沉井的附加应力即是 σz，由公式(1)求得。

在实际沉井工程中，土体所产生的附加应力不可忽略。图3 可以明显看出，其附加应力根据不同土体深度会呈现不同变化，这是土体应力扩散效应。考虑到应力扩散效应，在不同位置其应力体现并非均布，因此对于沉井工程，公式(1)的布辛内斯克理论解并不能直接运用，需要引入应力分布系数，它是r 与z 的函数[6]。定义如下：

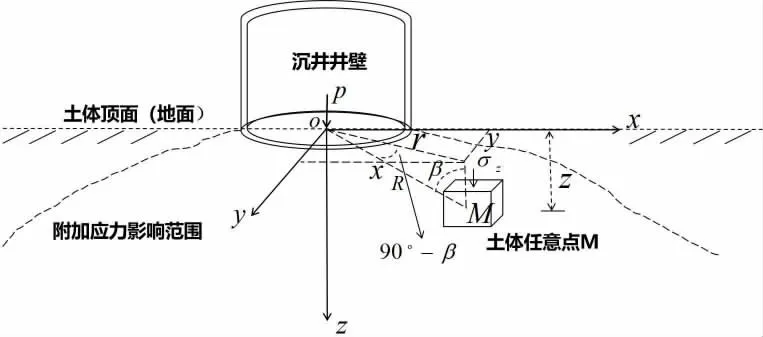
图3 沉井地基附加应力解析坐标系及简化力学模型

代入公式(1)，则改写成可以用于沉井附加应力计算的应力求解公式：

公式(4)可以直接用来求得沉井附加应力的大小，计算附加应力为土体固结度的分析奠定基础。在研究中发现，对沉井附加应力的计算的精确程度影响沉井对土的固结度的测算。测算的越准确，将越能控制住土体的变形，从而使得沉井下沉在可控之下，减少沉井挠度和偏移。

3.2 土体固结度分析

以上分析了沉井的附加应力分布，由此便可展开对沉井土体固结度的分析。分析固结度是为了能够准确把握沉井起沉力，以使沉井下沉到位。既不超沉，也不少沉。表征固结度首先从一点应力出发，由上述内容可知，沉井下沉时，土体中任意点M 所受的压力值，可根据公式(4)求得。为全面客观分析沉井对土体影响，认为土体是各向同性、均质、饱和的土；土层之间不发生渗流，土中所含水的渗流服从达西定律。则可以得出土体固结度表征：

其中，u 为土体受力变形的表征，t 表示土体作用时间，cv为土体固结系数，z 为土体沿z 向的变化分布情况。

通过公式(5)的计算式表明：土体固结度与土压在竖向的分布有关，在正常的沉井下沉土体分析中，需要及时明晰土体在竖向的分布态势，才能有效完成沉井。而实际工程中最关键的是要把握住固结系数，固结系数Cv的获取方法很多。可对土体进行试验测量，也可进行直接计算或平方根法等求得。

4 纠偏及挠度控制

沉井工程是一个持续不中断的施工过程，下沉的受力情形与简支梁受均布荷载体系类似[7]。故选择简支梁受均布荷载q 作用的力学响应为简化受力模型（如图4）。A、B 分别为简化后的支座。跨中为C 点，井壁开始下沉，则受到均布荷载q 作用。

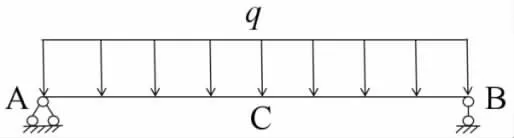
图4 沉井下沉受力简图

因此给出5 种跨度不同的简支梁，跨度分别为10m、20m、30m、40m、50m，将5 种情况带入进行计算。分析结果带入挠度与受力变化中。图5 计算得出挠度值与最大弯曲应力之间的关系曲线，通过这个曲线图分析结果。

图5 挠曲变形与跨中最大弯曲应力关系曲线

图5 结果显示，随着跨中挠度值的增大，最大弯曲应力值也持续增大。这个结果说明沉井直径越大，其下沉难度越大，越需要精准刻画沉井的位置，否则将产生较大挠曲变形，影响沉井井壁质量。基于前述分析，沉井的动态控制是建立在图里盈利状态的分析基础之上的。大量沉井工程实践已经表明：在正常沉井的过程中，土体发生相对运动，沉井发生管涌的风险极高，表征为沉井发生不均匀性偏位，偏移后的井壁会有失效的可能，而为防止其偏移，应该匀速缓慢下沉，同时做好平面控制和下沉过程中控制。

5 结论

本文从沉井破坏的机理出发，通过对沉井的土体附加应力效应、土体固结等方面进行分析，得出沉井的偏位和挠度原因与竖向压力分布有关，并从布辛内斯克理论解分析入手，对真实沉井环境下的土体受力情况重点分析，得出在真实条件下，土体在受到下沉井壁作用下，土体扰动形成土层相对运动，这种土体流动构成沉井下沉作业的弱侧限条件。并结合分析结果，得到在弱侧限条件下的沉井纠偏和挠度控制措施。