巧构回路 妙解异面直线夹角

◎孟 巍

(吉林省德惠市实验中学，吉林 德惠 130300)

一、试题呈现

案例1如图1，在三棱锥P-ABC中，PA⊥底面ABC，AC⊥BC，PA=AC=BC，则直线PC与AB所成角的大小是________.

图1

案例2如图2，四边形ABCD为菱形，∠ABC=120°，E，F是平面ABCD同一侧的两点，BE⊥平面ABCD，DF⊥平面ABCD，BE=2DF，AE⊥EC.求直线AE与CF所成角的余弦值.

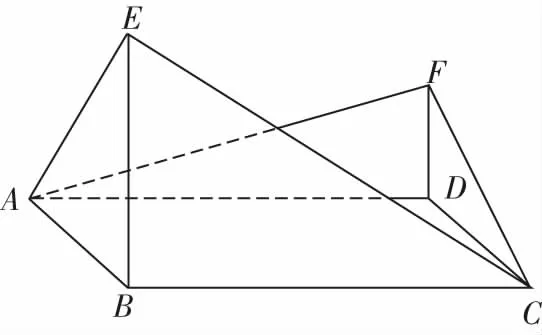
图2

二、解法展示

以上两个案例是求异面直线夹角的经典问题，解决异面直线夹角问题一般有三种方法，分别是几何法、坐标法和向量法.

(一)作辅助线，平移直线构夹角

案例1中，运用几何法，首先借助三角形的中位线定理作出两条辅助线EF和FG，将异面直线PC与AB的夹角转化为直线FE与FG的夹角(或其补角).然后构造两条辅助线EG和AG，根据勾股定理及余弦定理求得四条辅助线的长度，从而求得角度.

解取PA中点E，PB中点F，BC中点G，连接EF，FG，EG，如图3.

图3

∵EF，FG分别是△PAB，△PBC的中位线，

∴EF∥AB，FG∥PC，

∴∠EFG(或其补角)就是异面直线AB与PC所成的角.

连接AG，设PA=AC=BC=2，

则CG=AE=1.

∴PA⊥底面ABC，∴PA⊥AG，

根据余弦定理可得∠EFG=120°,

则异面直线AB与PC所成角的大小为60°.

(二)建坐标系，计算坐标推向量

案例2中，运用坐标法，首先选取底面菱形对角线的交点G为坐标原点来建立直角坐标系，然后连接EG,通过两次勾股定理的运用得到EB的长度，再根据DF与EB的关系确定E，F两点的坐标，最后利用向量法求夹角的余弦值.

解如图4,以底面菱形对角线的交点G为坐标原点建立直角坐标系.

图4

设GB为单位长度1，

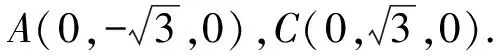
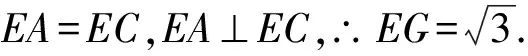
(三)构造回路，转化向量解夹角

案例1设PA=AC=BC=a，

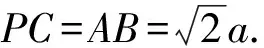
=a2,

故直线PC与AB所成角的大小为60°

案例2设AB=2.

=-3,

三、解后反思

(一)巧构回路，优化学生思维

教师应该重视介绍和引导学生用“回路 ”向量法来思考和分析问题，因为抓住 “回路 ”和选好 “回路 ”往往是解决不易解决或较难建立坐标系的异面直线夹角问题的关键与契机.通过构造回路，学生能得到有关联的向量积形式，从而直接算出结果.这种方法能优化学生的思维，巧妙构造回路的过程就是学生数学思维培养的过程.

(二)提升素养，回归向量本质

案例3在直三棱柱ABC-A1B1C1中，∠BCA=90°，M，N分别是A1B1，A1C1的中点，BC=CA=CC1，则直线BM与AN所成角的余弦值为( ).

解设BC=CA=CC1=m.

所以选C.

(三)拓展应用

图5

解法1(坐标法)

设圆台上、下底面圆半径分别为r，R.

∵πr2=9π，∴r=3.

∵πR2=36π，∴R=6.

过点B1作B1H⊥AB于点H，如图6，则HB=3，

图6

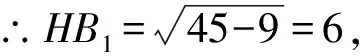
∵二面角B1-AA1-C1是直二面角，

∴建立空间直角坐标系A-xyz，如图7，

图7

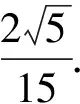
=-9，

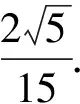
核心素养中提出要培育学生的直观想象能力，增强学生运用图形和空间想象思考问题的意识.向量作为几何和代数之间的桥梁，在研究几何中有着重要的作用.向量语言可以解决数学中的一些问题，向量中最基本的法则是三角形法则，也就是上文所说的回路.所以回路法也是一种回归基础、回归本质的方法，它既是平面向量教学的起点，又是空间向量教学的起点.通过构造回路建立起向量和几何之间的关系，学生可以用向量来解决几何问题.提升学生的数学素养是所有教师共同的目标，通过构造回路，学生能在理解向量本质的同时提升核心素养.