基于卷积神经网络的大肠杆菌启动子预测*

彭宝成 张晓炜 刘 暘 樊国梁**

（1）内蒙古大学物理科学与技术学院，呼和浩特 010021；2）内蒙古医科大学第一附属医院风湿免疫科，呼和浩特 010050）

启动子是基因序列中一段可以调控基因表达的核苷酸序列（序列中含有起始位点），控制着基因的表达与否，因此启动子在基因的转录和表达中具有重要的地位。

在大肠杆菌基因组中，启动子是一段分布于起始位点上游60 bp及其下游20 bp、包含起始位点的长度为81 bp的DNA碱基序列。按照Sigma因子的类别，大肠杆菌共有7种启动子，分别是Sigma19、Sigma24、 Sigma28、 Sigma32、 Sigma38、Sigma54、Sigma70。由于启动子序列具有保守性，根据保守性片段区域的不同，启动子又可以分为保守性区域在转录起始位点上游-10 至-35 位点附近的（以Sigma70 为代表）和在转录起始位点上游-12 至-24 位点附近的（以Sigma54 为代表）保守性启动子［1-2］。

大肠杆菌的分布极广，并且作为肠杆菌类的成员经常被作为细菌模式生物而被广泛研究，因此人类对于大肠杆菌的研究非常深入（生物实验方面）。大肠杆菌所有系列的基因序列已经在20 世纪被完全测量，但是基于生物实验方法寻找启动子的方式十分耗时、昂贵。虽然它可以较为准确地定位启动子序列，但是在面对海量数据时，效率低的弊端开始凸显，因此计算生物学的研究应运而生。以往的研究者提出了各种各样的模型并且取得了良好的预测效果［3-7］。2015年，丁辉等构建的三联体位置关联矩阵的预测方法，预测Sigma54 的精度达到82.0%［8-9］；2015年闫妍等［10］利用位点特异性打分矩阵（positive-specific scoring matrices，PSSM）方法预测Sigma 启动子，模型对Sigma54 的预测准确率为97.4%，对Sigma38 的预测准确率为96.0%，对Sigma70 的预测准确率为74.0%。此外还有基于柔性参数+二联体位置关联权重矩阵［11］、位置关联打 分 特 征（position-correlation scoring feature，PCSF）+ 伪核苷酸特征（pseudo k-tuple nucleotide composition，PseKNC）［12］、启动子元件的位置权重信息+k-联体核苷酸频率等方法，后来的趋势表明，研究者趋向于组合多种特征来定义启动子序列［13］，以至于分类特征维数急剧增加，因此不得不在分类时对数据进行降维处理。在算法方面，常用的机器学习算法有支持向量机（support vector machine，SⅤM）、随机森林、K-近邻、隐马尔科夫、人工神经网络、前向传播算法等或其他算法如线性判别分析、二次判别分析等［14-19］。近些年深度学习算法也逐渐被研究者所关注，并且已有研究者将卷积神经网络（convolutional neural networks，CNN）应用于大肠杆菌启动子Sigma70和非启动子的二分类预测中，对由A（1,0,0,0）、T（0,1,0,0）、G（0,0,1,0）和C（0,0,0,1）编码的向量序列进行预测得到了敏感性Sn（sensitivity）=0.90、特 异 性Sp（specificity） =0.96、 准 确 率Acc（accuracy）=0.84 的结果，但准确率仍需进一步提高，编码方式仍需优化［20］。

1 数据集的构建和特征算法

1.1 数据的选取

论文中采用的Sigma38、Sigma54、Sigma70数据集可以从RegulonDB 10.8（http://regulondb.ccg.unam.mx/Downloadable）下载，为了便于后续数据处理，保证数据的一致性，对数据文件做如下处理：

a.剔除Sigma Factor that recognize the promoter标注为多种类型的行。

b.删除文件信息（以“#”开头的行）和序列信息列（如“acrDp2”等信息），只留下序列所在列。

c.删除没有序列内容的行。

经过处理后得到了Sigma38 序列146 条、Sigma54 序 列96 条、Sigma70 序 列810 条，共 计1 052条，作为正集。启动子序列的长度均为81 bp（-60 bp～20 bp，设基因转录起始位点为0）。

分别选取了300 条编码区序列和300 条基因间序列，长度均为81 bp，作为负集。基因间序列处于两条基因之间的区域，选取中央区域可以最大限度的避免选入启动子序列。

1.2 特征描述

大肠杆菌基因序列为字符序列，而CNN 算法（目前为止的大部分算法）能处理的只有数值序列，因此需要将字符序列转换为数值序列，这一步也被称之为特征提取（或采样）［21-22］。在转换过程中丢失的信息越少则对序列的描述也就越精确。首先，每一类序列的训练集分别构建了位点特异性打分矩阵。其次，利用该PSSM对该种类的训练集和测试集打分，从而将字母序列转变为数值序列。

1.2.1 构建位点特异性打分矩阵特征

a.构建频数矩阵

将序列坐标化（从0 ～80共81个位点），统计每个坐标上A、G、C、T 4种元素出现的频数，如果存在坐标点上面某种核苷酸出现的次数为0，则需要引入伪计数（即将该位点上所有类型核苷酸的频数加一整数，本文中加1）。最终形成的频数矩阵列名为序列坐标（s1～s81），行名为4 种核苷酸（A、G、C、T）。

b.生成频率矩阵（伪计数频率矩阵）P

计算每种核苷酸在该位点上出现的频率，即用该位点上每一种元素的频数除以该位点上所有元素的频数和，其中xi,j是在i位点上第j种元素的频数，Pi，j是在i位点上第j种元素的频率：

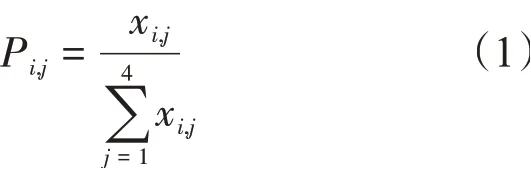
c.生成对数几率比矩阵oddratio：

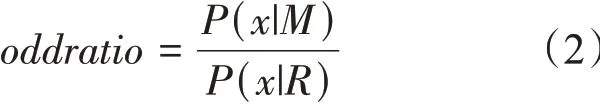
其中P(x|M)为核苷酸出现的实际概率，P(x|R)为核苷酸出现的随机概率（即0.25），因此将频率矩阵P中的每个频率值除以0.25 即可得到oddratio。随后对oddratio求以2 为底的对数，该矩阵即为位点特异性打分矩阵，矩阵的大小为（4×81）维。

1.2.2 对特定序列打分

从PSSM 矩阵中查出特定位点上核苷酸的分值，对给定序列赋值。实现方式是矩阵点乘，最终可以得到1×81或者4×1×81的矩阵（即一维矩阵或者四维矩阵）（图1）。

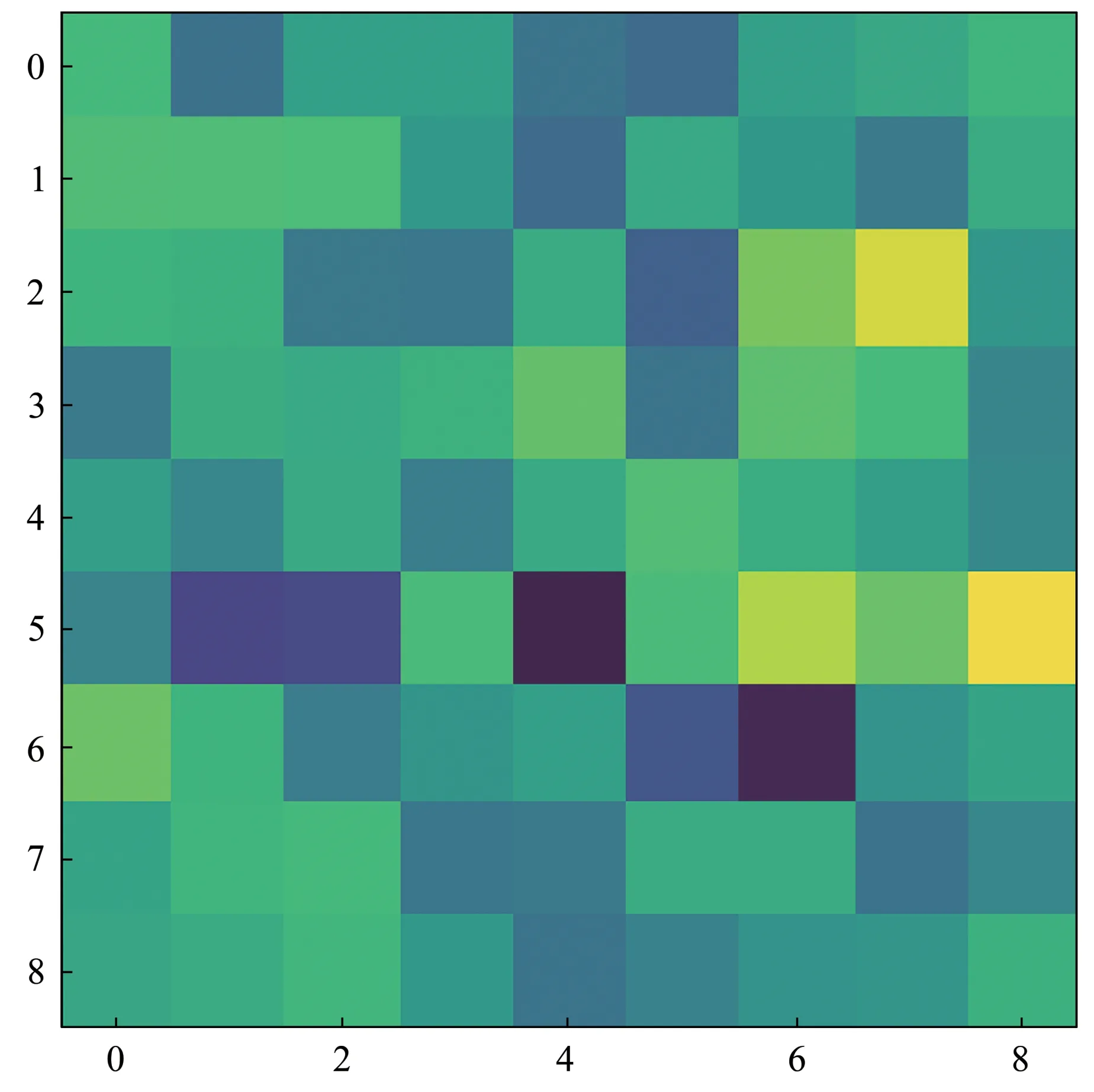
Fig.1 Sigma70 sequence matrix pixel matrix bitmap after scoring by PSSM

这里的维度指的是通道数：RGB图片有3个通道（R、G、B）即通道数为3，每个维度上的每个位点的数值即为该通道在该位点上的通道颜色浓度，取值范围为0～255，一张RGB图片数值化后就是一个三维数值矩阵（图2）。

类似的，可以把A、G、C、T 作为4 个通道，将序列数值化的方法就变得容易理解：一条序列在A通道（A通道长度为81）上每个位点的值可以是0（该位点不为A）或者1（该位点为A），对其他3个通道做同样处理，结果如图3c 所示。计算证实训练上述方法得到的01 数值序列也可以获得好的效果，但是01 离散数字序列携带的只有位置分布信息，信息量过小，因此过拟合的现象常常发生。

把A 通道中的1 替换成PSSM 中的打分值。在位点s1上，“g”的打分值为-0.497 5，那么G通道中位点s1 上的1 就可以被替换为-0.497 5，如果是0则不需要替换（表1）。这种方法显然可以让数值化序列带有更多的信息，对其他通道做同样处理，就构造出了4个维度的数值矩阵（图3d）。

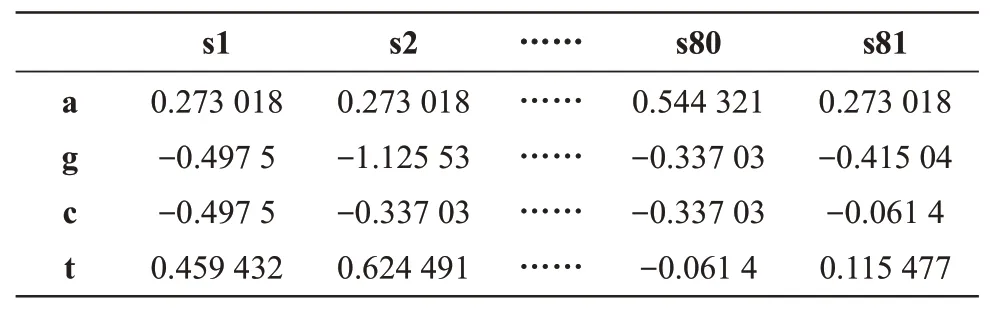
Table 1 Sigma70 position-specific scoring matrix（PSSM）for a certain training set

图片上每个色块的颜色是由3个通道颜色组合而成的，与此不同的是，启动子序列的每个位点只有1个通道的值（AGCT中的一个）（图3b），因此每个通道中依旧有很多的0 存在（图3d），所以可以将4个通道对应位点的数值加和，得到一个没有‘0’的长度为81 的向量（图3e），将向量变换成9×9的矩阵绘图以后形成的点阵图片（图1）。依旧是由于序列和图片的不同点，序列的四维数值信息和一维数值信息没有本质上的区别，反映在模型表现上就是预测的准确性没有大的差别。

Fig.2 Picture of RGB three-channel schematic diagram

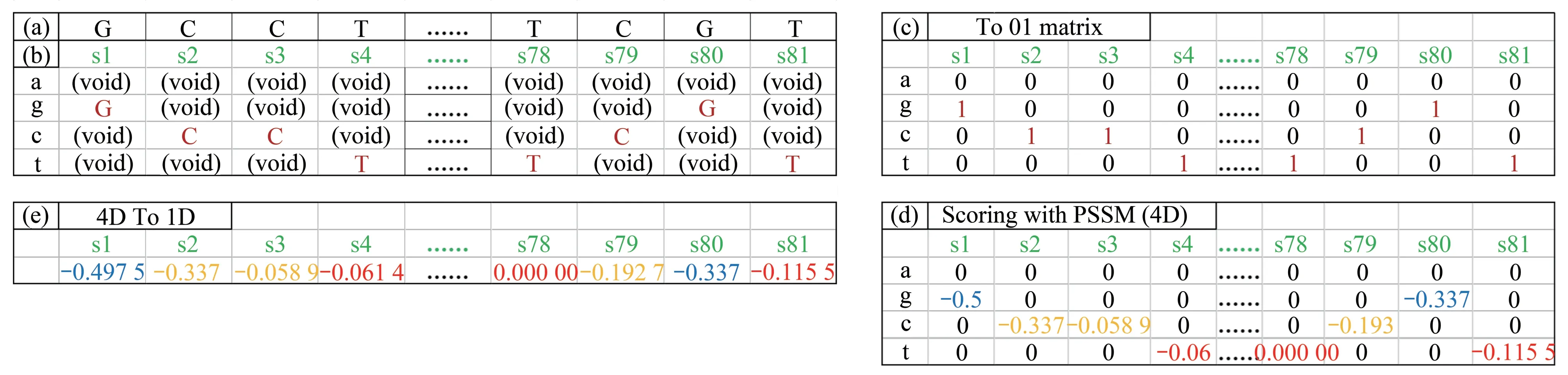
Fig.3 Overview of conversion method for certain Sigma70 sequence

与图片信息相同的是，启动子的保守性区域可以类比为被人类所理解的图像信息（如数字“1”反映在图像上是几个白灰色像素块组合，图4），无论是保守性序列还是数字“1”都具有不变性，这为研究者们寻找启动子的独有特征奠定了理论基础［23］。

Fig.4 Handwritten numbers “1” from http://deeplearning.net/data/mnist/

1.3 分类算法

CNN 是一个兼顾全连接和卷积取样的前馈神经网络算法，它的提出来源于对生物的视觉皮层研究。它在处理多层网格结构数据方面具有巨大优势，因此现在CNN 被广泛应用于图像识别、语音识别和自然语言处理等领域。CNN 的实现分为两个主要步骤：a.数据的预处理：将图像等信息数字化和去噪等操作；b.特征提取和分类：这一部分由CNN 网络结构来实现，基础的网络结构包括卷积层、池化层和全连接层3 部分，深度CNN 是基础网络结构的多层叠加，这样可以实现更多特征的提取从而提高识别精确度。

CNN 的主要特点有局部区域连接、权值共享和降采样。a.局部区域连接（图5 左），即前后两层网络的所有神经元并不是都互相连接的，目的是为了模拟视觉神经的选择性聚焦，这有利于减少训练参数；b.权重共享，即一个卷积核在提取特征时的权重在整张图片上都相同，这意味着一个卷积核只能提取一种特征；c.降采样，主要有最大值、平均值（图5右）和方均值保留等方式，通过池化层（pooling layer）实现，目的是为了降低特征分辨率和减少过拟合风险。由于这3个特点，CNN在抽取特征时更能够聚焦图片的重要信息（图4中黑色的背景显然就不是有效信息，因此CNN 就不会着重关注）。由于启动子序列的类图片特点，将CNN作为特征提取和分类的算法是比较合适的选择。

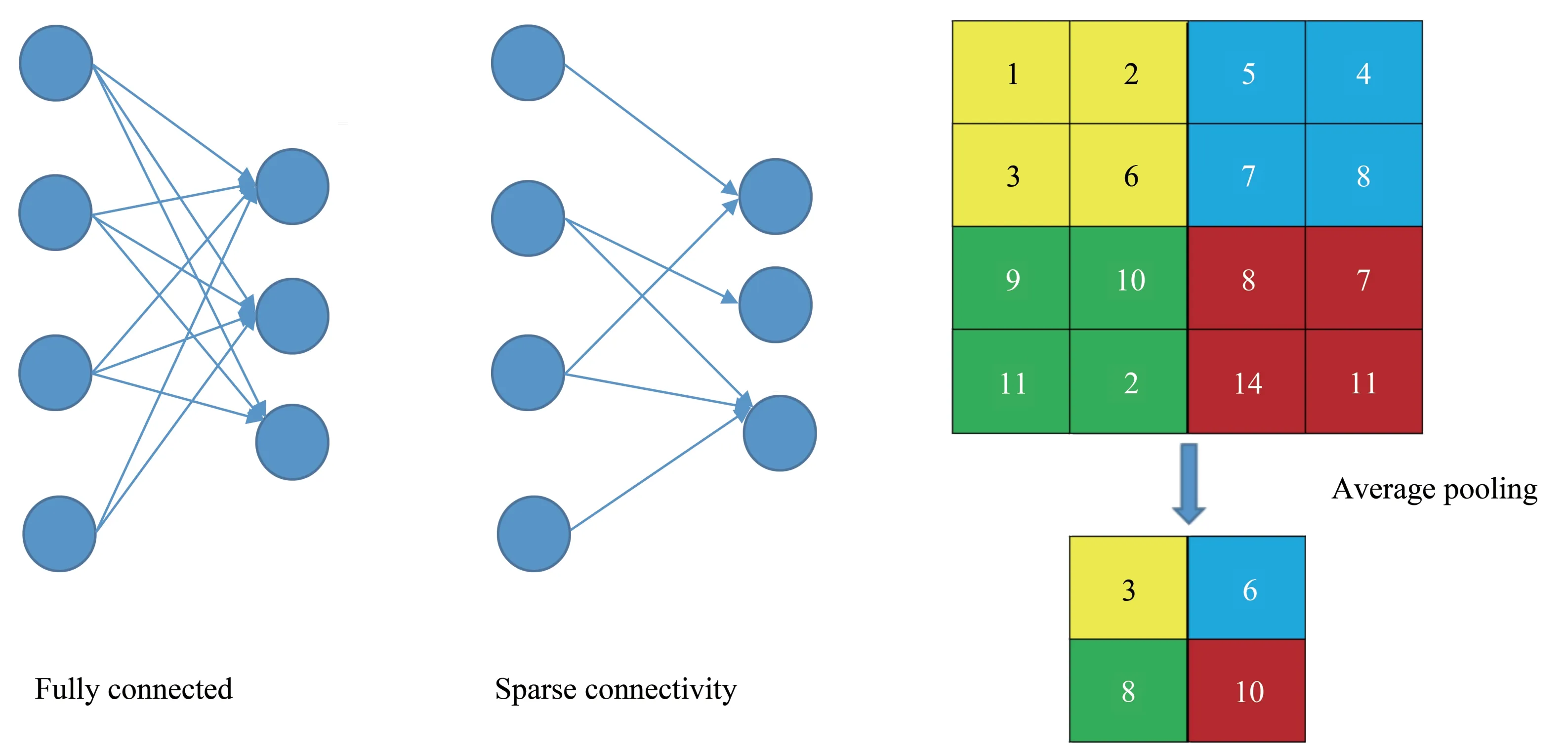
Fig.5 Fully connected layer and average pooling layer

2 检验方法

2.1 模型评价

2.1.1 自洽验证

分别从各类序列中抽取96 条序列组成均衡样本；构建均衡样本中每种序列的位点特异性打分矩阵（1.2 节），并按照1.2 节方式分别使用各自的位点特异性打分矩阵将各自的所有序列（包括均衡样本序列）转变成数值序列。以均衡样本序列作为训练集，采用全部序列测试模型性能。

2.1.2 独立检验

所有序列被分成两部分（数量均等），一份用做训练集，另一部分用作测试集，用训练集的位点特异性打分矩阵将测试集和训练集转变为数值化序列，使用训练集训练模型，测试集测试模型性能。

2.1.3 十交叉检验

该方法与前述独立检验不同的是，构建位点特异性打分矩阵所使用的序列数目不同。十交叉检验随机将数据集分成10份，取其中的9份构建位点特异性打分矩阵并被转换成数值序列后用作训练集，剩余1 份被转换成数值序列后用作测试模型性能。如此循环，则共产生了10 份测试结果，对10 份结果取平均就得到了最终的验证结果。

2.2 验证参数

2.2.1 ROC曲线

ROC 曲线即受试者操作特性曲线（receiver operating characteristic curve，常称ROC 曲线），描述的是在不同的标准下（主要是阈值），模型的击中率和误报率之间的函数关系。ROC 曲线常用在二分类模型当中，但是在多分类模型中也可以采取此参数（将被求ROC 参数的样本设为正集，其余种类为负集）。

曲线下面积（area under curve，AUC）一般在0.5～1 之间，AUC 越大即代表模型的性能越好。ROC 曲线的优势在于当正负样本数量对比发生变化时候曲线的形状不会变化。

2.2.2Sn、Sp、Acc

Sn、Sp常用在二分类模型验证当中，Sn表示正确预测正集样本的概率（式3），Sp表示正确预测负集样本的概率（式4）。

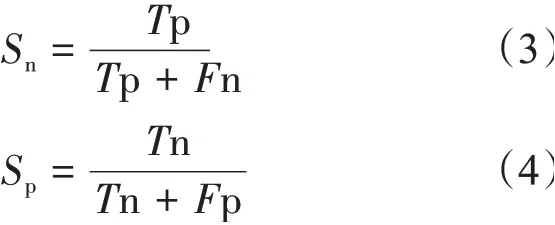
Acc无论是在多分类还是二分类都比较常用的参数，它表示样本被正确预测的概率：

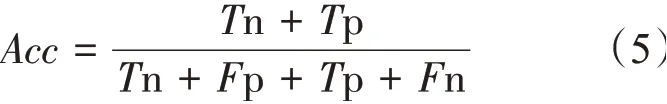
每个种类序列的准确率Acc公式为：

在Acc的计算公式中，Tn 和Tp 分别表示被预测成功的负集样本数和正集样本数，Fp和Fn则表示被预测失败的负集样本数和正集样本数。

在Acc的计算公式中，T代表该类序列中被预测正确的数目，P代表该序列中被预测失败的数目。

3 结果评估

本文采用PSSM矩阵作为识别序列的特征，用打分的方式将字符序列转变成数值序列。基于实际需要，本文做两组四分类：Sigma 序列和编码（Coding） 序 列、Sigma 序 列 和 非 编 码（Noncoding）序列。

3.1 损失函数

模型训练中使用的是交叉熵损失：

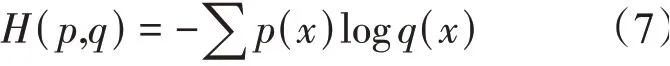
p(x)代表真实概率分布，q(x)代表预测概率分布，交叉熵损失是对两个概率分布差距的评估。交叉熵的函数图像（以Sigmod 函数作为激活函数）（图6），可以看到交叉熵图像具有单调性并且损失越大梯度越大，因此训练时权重可以很好地进行更新。

3.2 自洽检验预测效果

自洽检验的目的是为了证明模型的合理性，由于样本不均衡可能带来收敛难度增大等问题，数量过多的样本可以被人为地随机丢弃一部分，使要进行分类的各种序列数量保持一致（即达到样本均衡），并且将分布均匀的样本作为训练集，测试对全部样本的预测能力，以此来检验均衡样本对总体样本的预测能力（图7）。

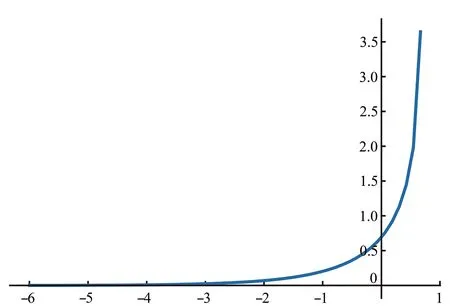
Fig.6 Cross_Entropy curve

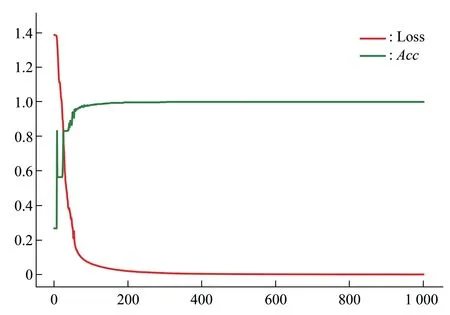
Fig.7 Self-consistent verification training curve

对样本参数进行评估，可以看到整体的预测性能比较好，各项参数都有比较好的表现（表2）。

Table 2 Self-consistent verification overall evaluation Parameters

图8为两种预测模型的ROC 曲线，每个种类模型的AUC 值均在0.96 以上，模型表现出了良好的分类能力。

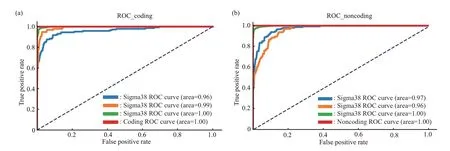
Fig.8 Self-consistent verification of two four-category ROC curves

需要注意的是，均衡样本的优势在于可以快速收敛并且可以有效地防止过拟合现象的发生，它的训练次数较少并且学习率较高，使用的分类器较少，可以很好地减少内存损耗，预测精度也十分可观。人为制造均衡样本的缺点在于训练集可能不能完全包含样本的所有特征从而影响预测准确率，为此通过对量大的样本进行多次采样，然后生成多个分类器，最后对所有分类器结果求平均可以解决此问题。

3.3 独立检验

从图9中可以看到独立检验的训练取得了良好的效果，损失函数曲线以及准确率曲线都比较平

Fig.9 Independent inspection training curve滑，这说明训练的过程比较顺利。可以看到准确率曲线最终上升到了1.0，损失函数下降到了一个较低的位置（0.000 6）。

第999 次的准确率为tensor（1）；第999 次的损 失 函 数 为： tensor （0.000 6， grad_fn=＜NegBackward＞）。

下面的表中展示了独立检验的验证结果（平均结果），With-coding 表示Sigma 和Coding 序列的验证 结 果（表3），With-Noncoding 表 示Sigma 和Noncoding序列的验证结果（表4）。

Table 3 Independent inspection result（With-coding）

Table 4 Independent inspection result（With-noncoding）

表3、4 显示Sigma38 序列相对于其他启动子的准确率明显较低，这可能是由于过拟合导致的，在训练中Sigma70也较容易出现这种情况。

独立检验绘出的ROC曲线（图10、11），可以看到无论是哪种样本组合，曲线的表现都十分让人满意。相对地来说，Sigma38的结果较差一些，这也是和上面的Acc结果有很好的对应。

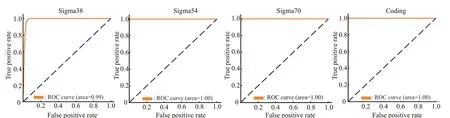
Fig.10 Independent inspection ROC curve(With-coding)

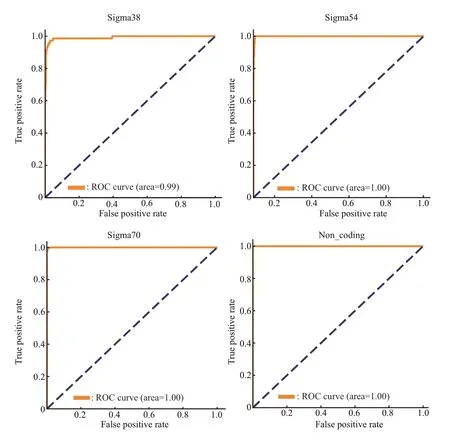
Fig.11 Independent inspection ROC curve(With-noncoding)

独立检验的结果证明（表5），训练非均衡样本依然是可行的途径，这主要归功于CNN 分类算法的高精度和PSSM 能够较好地代表序列的特征。但是非均衡样本会带来收敛过慢甚至出现无法收敛的灾难，因此常常需要对其进行过采样处理（采用较低的学习率和较多的训练次数、更多的分类器以提取更多特征，如本次卷积层使用了16×16甚至是20×20 的卷积核，而均衡样本使用的卷积核为5×5），这样就又增大了过拟合的风险，因此训练成功的难度也相较于均衡样本高，并且它对算力的损耗也增大了。

Table 5 Independent inspection overall evaluation parameters

3.4 十交叉检验

为了节省算力开销，实验结论通过十交叉检验法被验证（表6～8）。

Table 6 Ten-fold inspection result(With-coding)

Table 7 Ten-fold inspection result(With-noncoding)

Table 8 Ten-fold inspection overall evaluation parameters

绘出的ROC曲线如下：

启动子和Coding 区序列四分类的ROC 曲线（图12）均在对角线上方，并且AUC值均比较接近1（Sigma38 的AUC 值为0.97，Sigma54 和Coding 序列的AUC 均为0.99，Sigma70 为0.96），这表明模型对于启动子的分类效果比较理想。

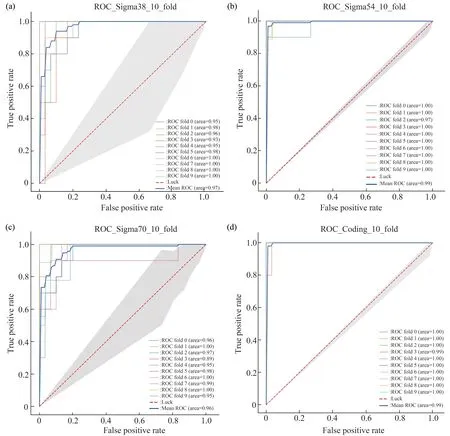
Fig.12 Ten-fold inspection(With_coding)ROC curve

在启动子和Non_coding 区序列四分类的ROC曲线（图13）中，Sigma54序列和Non_coding区序列依旧达到了0.99，Sigma38 的AUC 值上升到了0.98。

Fig.13 Ten-fold inspection(With_noncoding)ROC curve

在十交叉检验的结果中，可以看到模型对于四分类的整体预测准确性都达到了0.97以上，并且对每一种序列的预测精确性也都达到了0.95以上。

3.5 对比分析

采用PSSM特征和采用二联体+柔性参数［11］两种方法得到的准确性（表9）结果的对比数据显示：PSSM特征的预测效果更为理想，并且采用本论文中方法取得的效果远远好于二联体+柔性参数的方法，这说明PSSM特征对于序列特征的描述更为精确。

单独使用PSSM 特征分类和采用PSSM 特征+CNN 算法分类两种方式对Sigma38、Sigma54 和Sigma70 的预测结果（表9）的对比数据显示：CNN算法对3种启动子的预测准确性都优于仅仅使用PSSM 特征分类的方式，而且CNN 算法对每种启动子的预测准确性都比较均衡，没有出现对某个启动子预测精度过小的现象.

为了更进一步探究算法对启动子和非启动子的分类效果，两种方法（表10）对相同的数据集预测并且进行了十交叉验证，对比结果显示：本论文中的方法取得了更理想的结果。本论文方法在不同分类条件下得出的结果（表9，10）对比显示：二分类的效果要好于多分类。

本论文取得的成果与同行的最新研究成果对比显示（表11）：Grad-CAM 编码方法（Feature by Grad-CAM）可以取得稍好的准确率，但其特异性尤其是AUC 值表现较为逊色，说明其模型稳定性可能存在问题，本论文则兼顾了准确率和模型参数两方面。独热编码（one-hot encoding）方法取得的准确率为0.901，AUC值为0.957 2，本论文的结果相对较好［24-25］。

Table 9 Comparison of Acc（Ten-fold inspection）

Table 10 Comparison of comprehensive parameters（Ten-fold inspection）

Table 11 Comparison of comprehensive parameters(with the newest results)

4 讨 论

CNN+PSSM 方法采用的特征简单易用，并且多分类可以大幅提高预测效率。有研究者单独采用PSSM打分进行分类，这种方式取得的效果稍逊于本文方法，主要原因可能是PSSM 特征稍显简单。在没有有效算法辅助的情况下，这种分类方式相对利用更复杂、覆盖差异更全面的特征描述方法表现确实逊色。但是这并不意味着利用简单的特征描述方法得不到好的结果。Shujaat等［24］和Zhang等［25］都利用较简单的特征描述（01 序列为基础）得到了较好的预测结果（前者97%以上，后者80%左右）。其次是在分类算法上，Shujaat 等［24］采用了过于简单的01序列造成了很大的泛化，本身01序列蕴含信息就比较少，再次提取特征只会让CNN模型的过拟合风险增大。Zhang 等［25］虽然取得了较好的准确率，但是在AUC（仅在0.84 以上，且Sigma38的AUC为0.63）和Sp（0.78以下）等模型评估参数的表现上不如人意，其采用的序列转换方法（由字符序列转换为数字序列的方法）也是01编码方式。

样本不均衡容易造成训练的泛化，目前还没有好的调参办法来完美解决这一问题，并且这一点也常被同行研究人员所忽视。目前大多数深度学习的研究者采用的方法是减少训练样本中数量过多的种类的数量，人为地调整样本分布，或者采用过采样的方式对数量较少的种类重复取样。有研究者提出过采样可能是在以ROC/AUC作为评价指标时最佳的处理方式［26-27］。为了减少模型拟合困难问题的发生，本文采用了人为调整样本数量的方法，剔除了过多的样本。

CNN 和PSSM 特征结合是采取了两条腿走路的方法：选取良好的特征描述方法可以最大限度的覆盖不同种类启动子之间的差异，为CNN 提取差异进而进行有效的分类奠定基础；CNN 自学习的优良特性和对算法的优化也是提升模型性能的关键。由于PSSM 特征对启动子序列描述较为全面，因此本方法在序列转换过程中丢失了更少的信息，同理如果可以选择特征描述更为全面的转换方法，模型的准确率会有进一步的提升。

5 结 论

本论文通过构建样本的位点特异性打分矩阵，并且使用样本的位点特异性打分矩阵将待预测的字符序列转化成数值序列。利用PSSM特征训练出来的CNN 模型对Sigma38、Sigma54 和Sigam70 3 种序列进行预测，分别得到了0.978 9、0.995、0.964 4的预测精确度。

在将序列数值化的过程中，PSSM特征能够很好地表征每种序列的核苷酸分布信息，这使得每种序列之间的区分度比较明显。由于PSSM特征的构建方法简单，因此该特征对于序列的特征表述不会过于冗杂，这有效地降低了CNN 在训练模型时发生过拟合的风险。本文提出了一种解释序列特征的新思路，即利用类图片特征构建序列的点阵图像，这为下一步研究序列特征提取提供了一个新的方向：例如，如果可以基于PSSM再创造一套多通道的标准（类似于RGB标准），让每个位点的数值由多个通道共同决定，那么将序列展开为多维矩阵的识别效果可能更好［28］。