核脉冲信号冲激成形的导数求解方法

汪雪元 周建斌 何剑锋 王 明 汤 彬 洪 旭 刘 易

1（成都理工大学核技术与自动化工程学院 成都 610059）

2（东华理工大学核资源与环境国家重点实验室 南昌 330013）

核脉冲信号冲激成形常用来获取入射粒子的数量信息和时间信息，广泛应用于核辐射的强度测量、高分辨能谱分析、高计数率能谱校正以及符合反符合测量。核脉冲信号的数字成形是数字核仪器研制的研究热点［1-4］。核脉冲信号的数字冲激成形是数字成形中的一项关键技术［5］。

文献［6］基于Z变换给出了一个核脉冲信号冲激成形算法，用于高计数率场合的核脉冲信号计数率测量。文献［7］基于CR 微分成形电路原理给出了一个核脉冲信号冲激成形算法，用于X 射线光谱测量中的计数率测量。文献［8］中用标准负指数函数描述核脉冲信号，然后对信号进行反褶积运算，得到冲激响应函数。文献［9］给出了一个基于单指数输出信号模型和一阶导数的辐射测量系统的冲激响应函数。文献［6-9］中给出的核探测系统输出信号模型比较简单，有时候并不能精确描述要成形的核脉冲信号。基于Z变换的冲激成形算法原理简单，但在探测系统输出信号模型较复杂时，基于Z变换得到的冲激响应数字解变得复杂，且得到的数字解往往是递归表达式，这导致计算量较大，影响脉冲信号的成形速度。基于反褶积运算的冲激成形算法，在探测系统输出信号模型较复杂时，同样存在计算量较大的问题。

本文基于单位阶跃函数和单位冲激函数的微分积分关系，给出了一个核脉冲数字信号冲激成形的时域求解方法。应用新方法对模拟核信号和实际采样核信号进行冲激成形，并与基于Z变换的传统冲激成形方法进行了比较。

1 基于导数的核脉冲信号冲激成形方法

1.1 核辐射探测器系统输出信号模型

核辐射探测器系统输出信号模型可以用指数函数近似描述。常用的有单指数函数模型［10-12］和双指数函数模型［6-7］，数学描述分别如式（1）和（2）所示。

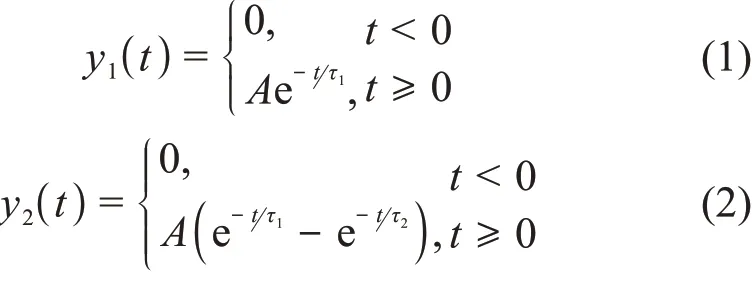
式中：t为时间变量，ns；A为常数；τ1和τ2为时间常数，且有A＞0和τ1＞τ2＞0。

文献［13］给出了一个半导体探测器输出信号的三指数函数模型。本文通过对核信号形状进行分析，给出了一个更为通用的输出信号三指数函数模型，如式（3）所示。

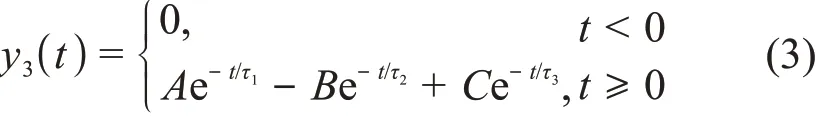
式中：τ1、τ2和τ3为时间常数，且有τ1＞τ2＞τ3＞0；A、B、C为值大于0的常数。且由合成信号初始值y3（0）=0，可知A-B+C=0。当C=0 时，有B=A，式（3）与式（2）等价，即式（2）是式（3）的特例。由式（2）对核信号进行拟合，得到的解集｛＜A，τ1，τ2＞｝是式（3）的解集的子集。从数学理论上可知，式（3）能够比式（2）更精确地对核信号进行描述。

同理，可以给出输出信号含任意指数项的通用函数模型，如式（4）所示。

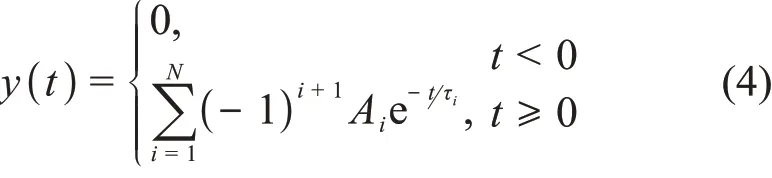
式中：N≥1。对于任意i，有τi＞0，Ai＞0。且对任意j＞i，有τi＞τj。当N≥2时，有

1.2 核脉冲信号冲激响应函数表达式

基于单位阶跃函数和单位冲激函数的微分积分关系，可以得到指数信号的冲激响应函数表达式。下面给出单指数输出信号冲激成形的数学推导过程。式（1）表示的单指数输出信号模型可以表示为：

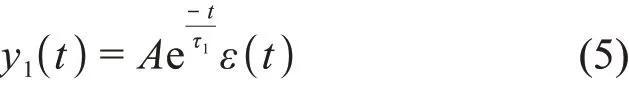
式中：ε（t）为单位阶跃函数。对式（5）的两端求导，得：

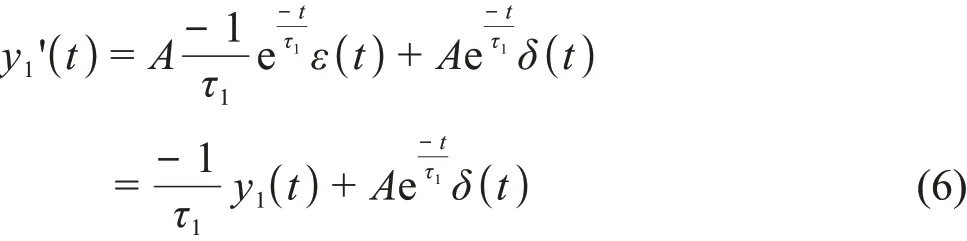
式中：δ（t）为单位冲激函数。移项，得：

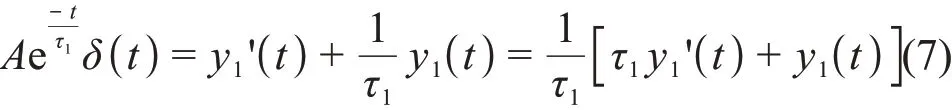
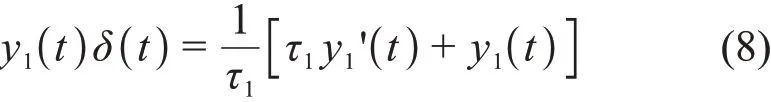
式（8）显示，单指数输出信号模型的冲激响应函数可以表示为输入信号y1（t）和其一阶导数的线性组合。

通过上述过程可以得到双指数、三指数及任意指数项输出信号模型的冲激响应函数表达式，分别如式（9）、（10）和（11）所示。

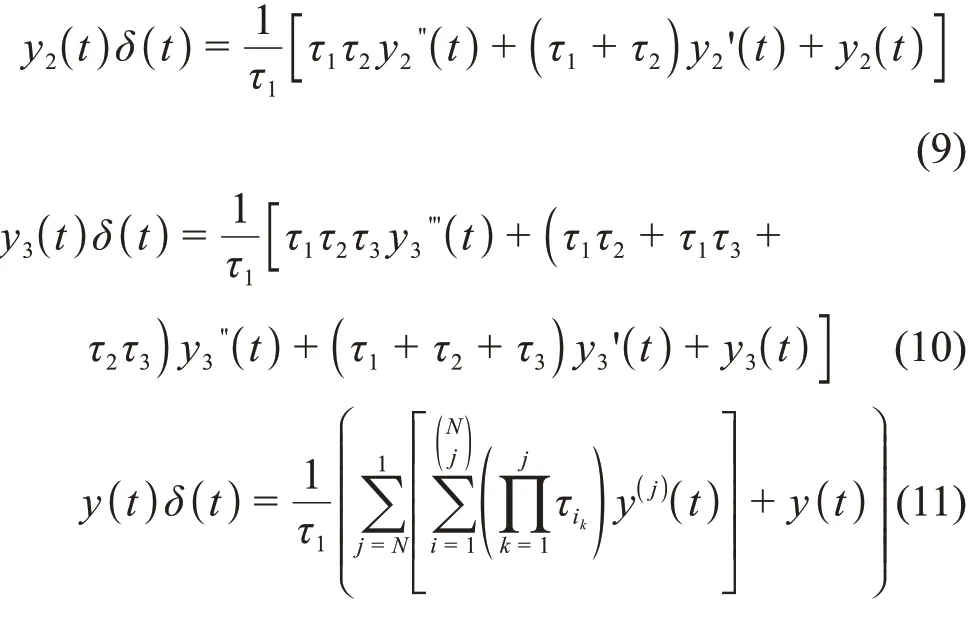
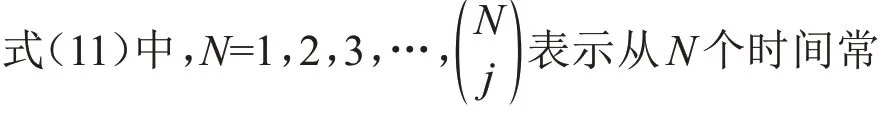
1.3 核脉冲信号冲激响应数字递推解

令Y［n］为探测器输出信号，P［n］为要得到的冲激信号。则式（8）、（9）和（10）的数字递推解分别如式（12）、（13）和（14）所示。

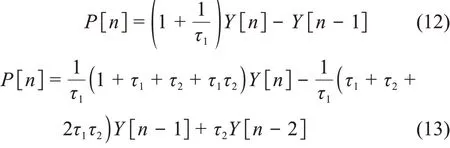
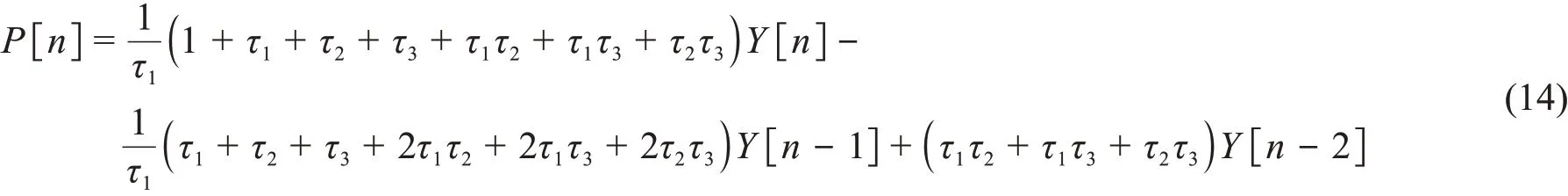
类推，也可以得到任意指数项输出信号模型冲激响应的数字递推解。从式（12）、（13）和（14）可以看到，基于导数运算的冲激成形算法的数字递推解非递归，且只含时间常数。

1.4 数字递推解中时间常数的确定

冲激响应表达式（8）、（9）和（10）为连续函数，当其转换成相应的离散数字递推解时，时间常数会发生微小畸变。当决定信号上升沿宽度的时间常数值较大时，微小畸变对信号冲激成形的影响较小。而当决定信号上升沿宽度的时间常数值较小时，微小畸变会对信号冲激成形产生较大影响，从而导致成形后的冲激信号产生下冲［7］。为了消除冲激信号的下冲，本文基于RC积分成形电路原理，建立了一种确定核信号冲激响应数字递推解中时间常数的方法。

RC电路是一种低通滤波电路，常用于核信号的积分成形。一阶RC积分成形电路和冲激信号的RC积分成形信号如图1（a）和（b）所示。

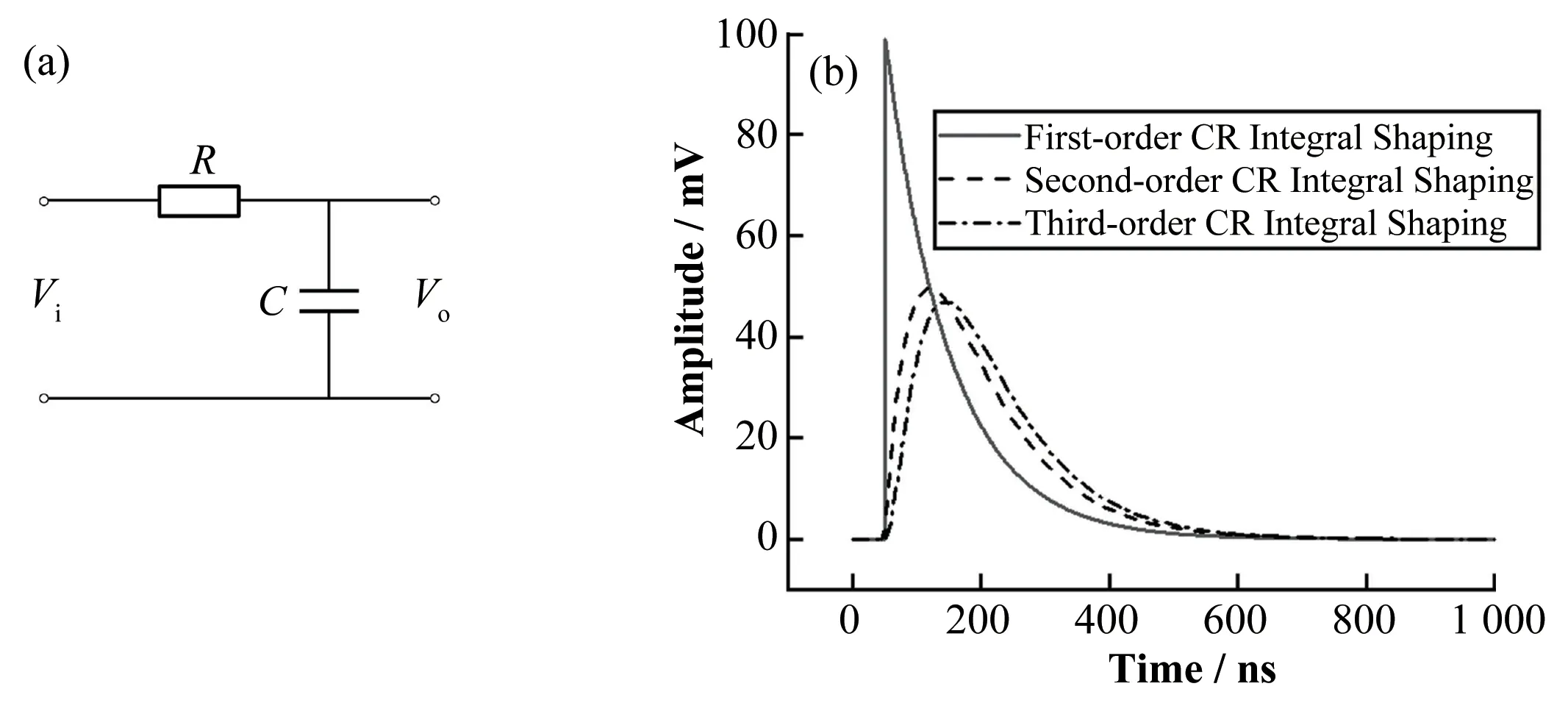
图1 RC积分成形电路和RC积分成形信号(a)一阶RC积分成形电路，(b)冲激信号RC积分成形（Amp=10 000,K1=100,K2=50,K3=20）Fig.1 RC integral shaping circuit and RC integral shaping signal(a)First-order RC integral shaping circuit,(b)RC integral shaping of impulse signal(Amp=10 000,K1=100,K2=50,K3=20)

图1中，Vi为输入信号，Vo为输出信号。取足够小的时间间隔，可以将Vi数字化为X［n］，Vo数字化为Z［n］，dt为采样时间间隔，n=1，2，3，…。通过基尔霍夫电流定律可以得到图1（a）所示RC电路的微分方程，进而得到一阶RC积分电路的递推数字解，如下所示［14］：

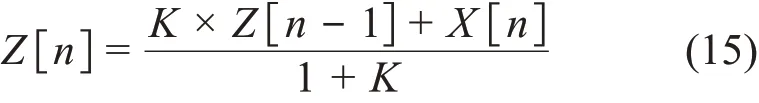
令K为100，应用式（15），对幅值为10 000 冲激信号进行积分成形，得到的一阶RC积分成形信号。令K为50，应用式（15），对一阶RC积分成形信号进行积分成形，得到的二阶RC积分成形信号。令K为20，应用式（15），对二阶RC 积分成形信号进行积分成形，得到的三阶RC积分成形信号，结果如图1（b）所示。

可以采用最小二乘曲线、遗传算法等方法，用一阶、二阶或三阶RC积分成形信号拟合目标核信号，求得数字解的时间常数。

2 冲激成形实验与结果分析

2.1 实验条件与实验流程

实验中使用的硅漂移探测器（Silicon Drift Detector，SDD）为Amptek 设计的FAST-SDD 探测器（XR-100 SDD）。探测器的能量分辨率为125 eV，峰值为5.89 keV。使用银（Ag）为靶材的X射线管照射锰（Mn）样品，X 射线管的电流设置为8 μA，而电压保持在35 kV。用真空泵抽真空，真空度约为0.09 mPa。数字系统中采用的模数转换器为AD9235，转换速率为20 MHz，分辨率为12位。

硅漂移探测器输出信号经线性放大器放大，然后由模数转换器进行采样。从模数转换器采集的原始脉冲数据，用于实验中的拟合与冲激成形。本文中的拟合与冲激成形，均为离线处理。实验中所用电脑配备了16 GB 内存和Intel CPU 内核（i5-6200U）。

核脉冲信号冲激成形的实验流程如下：

1）根据信号形状特征、系统精度要求，以及成形速度要求，选择冲激脉冲的一阶、二阶、三阶或更高阶RC积分信号对核信号进行拟合。本文中采用遗传算法求解，得到N阶RC积分电路递推数字解中常数Ki，其中i=1，2，…，N。

2）令时间常数τi=Ki，其中i=1，2，…，N。

3）应用核脉冲信号冲激成形数字解，如式（12）、（13）或（14），对核脉冲信号进行冲激成形。

2.2 模拟信号的冲激成形实验

令式（2）中A=10 000，τ1=37，τ2=2，得到上升沿较短的双指数模拟信号。对冲激信号进行二阶RC积分成形，得到二阶RC积分信号。用二阶RC积分信号与双指数模拟信号拟合，拟合结果如图2（a）所示。得到的二阶RC 积分时间常数K1和K2分别为37 和1.55。令τ1=37，τ2=1.55，由式（13）得到双指数模拟信号的冲激信号，如图2（b）所示。

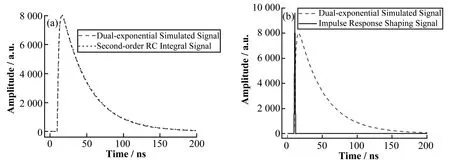
图2 双指数模拟信号的拟合与冲激成形(a)双指数模拟信号的拟合，(b)双指数模拟信号的冲激成形Fig.2 Fitting and impulse response shaping(IRS)of dual-exponential simulated signal(a)Fitting of dual-exponential simulated signal,(b)IRS of dual-exponential simulated signal

从图2（b）可以看到，成形后的冲激脉冲宽度为1，且基本没有下冲。这表明本文提出的基于导数的核脉冲信号冲激成形方法在理论上是可行的。

2.3 实际采样信号的冲激成形实验

用冲激信号的二阶RC积分信号对SDD实际采样信号进行拟合，得到时间常数τ1、τ2。将τ1、τ2代入式（13），得到实际采样信号的冲激信号。结果如图3所示。

从图3 可以看出，用本文提出方法对实际采样信号进行冲激成形所得到的冲激信号没有拖尾，且几乎没有下冲。这表明本文提出的基于导数的核脉冲信号冲激成形方法可以用于实际核脉冲信号的冲激成形。

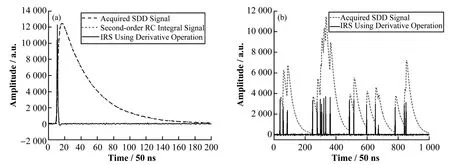
图3 SDD实际采样信号的拟合与冲激成形(a)实际采样信号的拟合与冲激成形，(b)高计数率场合实际采样信号的冲激成形Fig.3 Fitting and IRS of acquired SDD signals(a)Fitting and IRS of acquired SDD signals,(b)IRS of acquired SDD signals in high-counting rate environments

2.4 实际采样信号冲激成形结果线性分析

在相同实验条件下，用SDD半导体探测器对标准样品锰（Mn）、锌（Zn）、钢和铜合金进行测量，用模数转换器进行采样，获得100 s连续采样数据。应用本文提出方法，对实际采样信号进行冲激成形。由冲激脉冲幅度得到标准样品的能谱数据。对标准样品能谱进行寻峰，得到各个标准样品中所含元素特征峰信息。各个标准样品中主要元素K系特征X射线能量和对应特征峰道址如表1所示。

表1 标准样品中特征峰道址及能量Table 1 Channel and energy of characteristic peaks for standard samples

用x表示道址，y表示能量，对标准样品能谱特征峰寻峰结果进行线性拟合，拟合结果如图4所示。

图4中，R2的值为0.999 98，表明标准样品特征峰寻峰结果向量几乎完全相关。这表明本文提出的冲激成形方法对能谱没有显著影响，即冲激成形后的脉冲幅度与原脉冲幅度是线性相关的。

图4 标准样品能谱寻峰结果线性拟合Fig.4 Linear fitting of peak finding results for energy spectrum of standard samples

3 冲激成形方法的比较与分析

在核信号处理过程中，基于Z变换的核脉冲信号冲激成形是一种传统的数字冲激成形方法。基于Z变换的冲激成形算法原理简单，且成形效果良好。应用基于Z变换的传统方法和本文提出的新方法对模拟信号和实际采样信号进行冲激成形，然后对成形结果进行比较与分析。

3.1 基于Z变换的冲激成形方法

设输入信号Vi（t）如式（1）所示，Vo（t）为输出信号，得到系统函数如下：

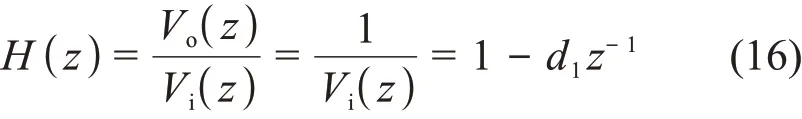
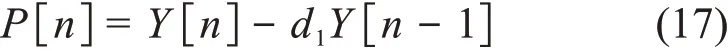
当Vi（t）如式（2）时，可以得到系统冲激响应的时域数字解如下［6］：

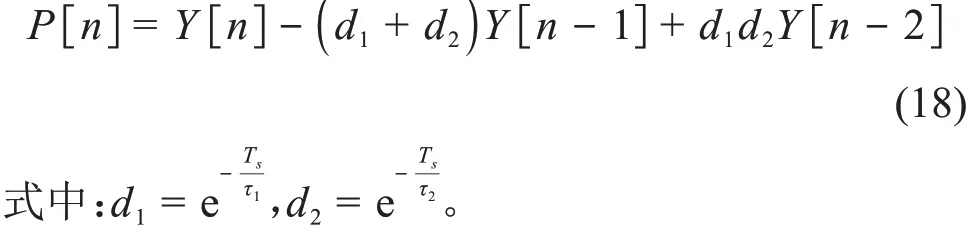
当Vi（t）如式（3）时，得到的系统时域数字解如下：

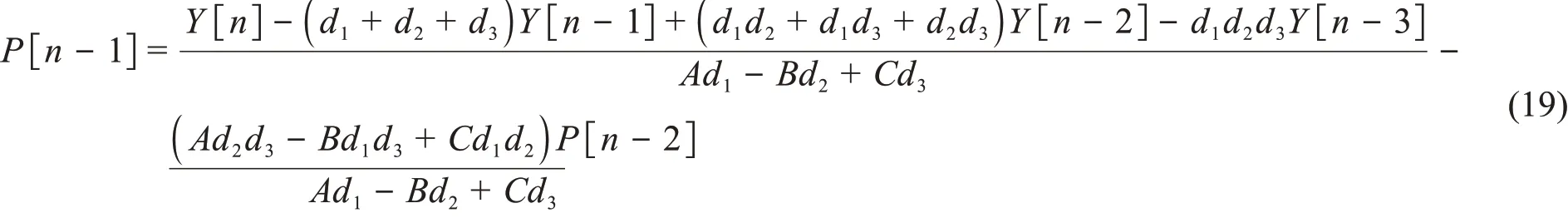
应用基于单指数输出信号模型得到的数字解，即式（17），对实测信号进行冲激成形时，冲激信号拖尾严重。而从式（19）可以看到，基于三指数输出信号模型得到的数字解中参数较多，使得获取参数值的拟合过程较为复杂。且式（19）的右式存在递归项P［n-2］。递归项的存在使得计算过程中的误差会累积传递，并影响最终结果。递归项的存在也限制了测量信号的高速流水线处理。实验中，式（19）对实际采样信号的冲激成形不够理想，冲激信号存在下冲、且噪声较大。在实际应用中，基于双指数输出信号模型的Z变换冲激成形算法，即式（18），常用于核信号的冲激成形。本研究中，对高计数率环境下的核脉冲信号，应用双指数Z变换冲激成形算法及本文提出的基于导数运算的冲激成形算法进行成形，并对成形结果进行比较。

3.2 重叠模拟信号冲激成形比较

令（A，τ1，τ2，loc）的值为（10 000，37，2，10）和（8 000，37，2，12）。其中loc为信号起始位置。由式（2）得到重叠双指数模拟信号。运用基于Z变换的传统方法和本文提出的新方法，对模拟重叠信号进行冲激成形，结果如图5所示。

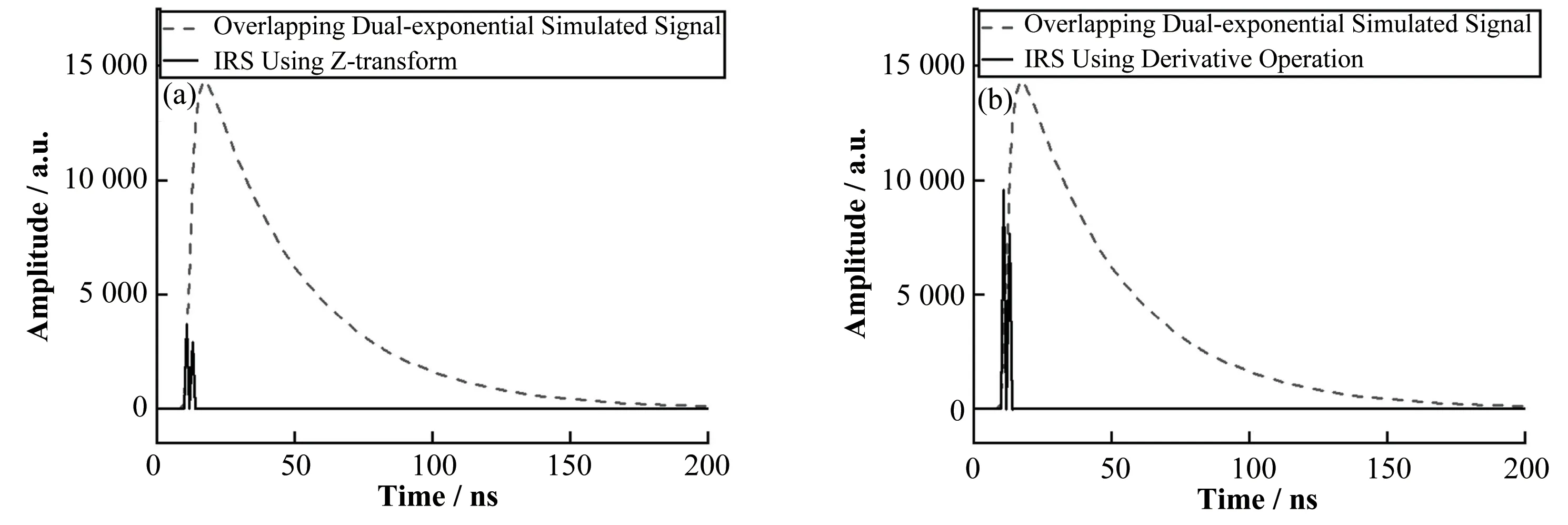
图5 重叠双指数模拟信号的冲激成形(a)基于Z变换的冲激成形，(b)基于导数运算的冲激成形Fig.5 IRS of overlapping dual-exponential simulated signal(a)IRS based on Z-transform,(b)IRS based on derivative operations

从图5 可以看出，本文提出的冲激成形方法与基于Z变换的冲激成形方法，都能够分辨出严重重叠信号。但从图5 还可以看到，由导数冲激成形得到的原始冲激脉冲比由Z变换冲激成形得到的原始冲激脉冲幅值更大。

3.3 实际采样信号冲激成形比较

用SDD 半导体探测器对锰（Mn）标准样品进行测量，用模数转换器进行采样，获得100 ms 的连续采样数据。运用Z变换冲激成形、二阶导数冲激成形、三阶导数冲激成形算法，即式（18）、（13）和（14），对获得的连续采样数据进行冲激成形，然后统计有效冲激脉冲数目。本文使用基于斜率、峰高两个阈值的寻峰算法确定有效冲激脉冲数目。基于Z变换的冲激成形方法获得了30 039个有效冲激脉冲。二阶导数冲激成形方法，获得30 070个有效冲激脉冲，与基于Z变换的冲激成形方法效果基本一致；三阶导数冲激成形方法，获得30 150个有效冲激脉冲，总计数增加了0.369%。重叠严重的核信号冲激成形的局部效果如图6所示。

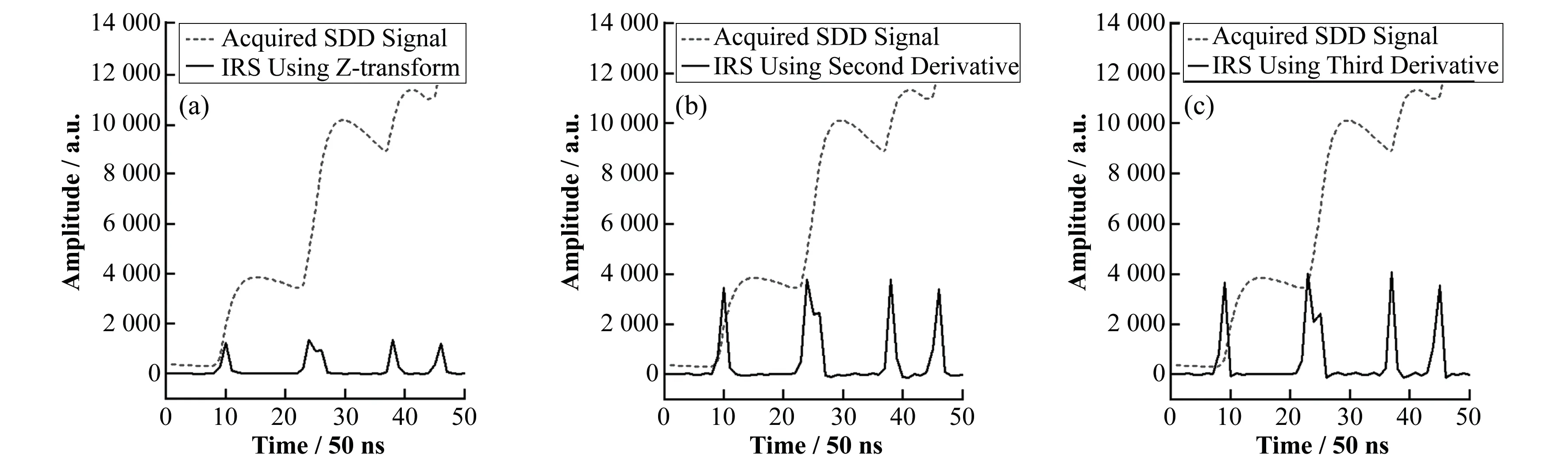
图6 SDD实际采样信号冲激成形(a)基于Z变换法的冲激成形，(b)基于二阶导数的冲激成形，(c)基于三阶导数的冲激成形Fig.6 IRS of acquired SDD signals(a)IRS based on Z-transform,(b)IRS based on second derivative,(c)IRS based on third derivative

图5中，横轴坐标20~30之间的冲激信号由两个冲激脉冲重叠而成。可以看到，二阶导数冲激成形与基于Z变换的冲激成形，得到的重叠冲激脉冲分离度基本一致。而三阶导数冲激成形所得到的冲激脉冲峰形更明显，重叠的冲激脉冲分离度更高。从图5还可以看出，导数法相比Z变换法，冲激成形得到的信号噪声变大了。导数阶数越高，噪声越大，但重叠信号的分离度也越高。

实际采样信号的冲激成形实验结果显示，Z变换冲激成形与导数冲激成形的成形效果基本一致。但本文提出的导数冲激成形方法，在严重重叠核脉冲信号的成形能力上优于基于Z变换的传统冲激成形方法。

4 结语

本文基于冲激响应与阶跃响应的微分积分关系，给出了核信号冲激响应的离散数字递推解。并基于RC 积分成形电路原理，给出了一个求冲激响应数字递推解中时间常数的方法。对模拟核信号和SDD 实际采样核信号进行冲激成形。从实际采样核脉冲信号的数据处理结果可以看出，基于文中构建的新算法可以得到稳定的核脉冲信号冲激成形结果，冲激脉冲的宽度在1~3 个采样点之间，反冲很小，拖尾几乎没有。实验结果显示，与基于Z变换的传统冲激成型算法相比，新算法在重叠核信号的识别方面，分辨能力更强。对采样时间为100 ms的标准样品锰（Mn）的连续采样数据进行冲激成形。相较于基于Z变换的传统冲激成形方法，基于三阶导数的冲激成形得到的有效冲激脉冲总计数增加了0.369%。文中给出的核脉冲信号冲激成形数字递推解，形式简单，非递归，只含时间常数。新方法适合不同精度要求和成形速度要求的应用场合，尤其适合高计数率场合的冲激成形。新方法对于建立高分辨能谱测量系统，符合反符合测量系统以及高计数率校正系统都有一定的意义。

作者贡献声明汪雪元、周建斌、王明：材料准备、数据收集和分析；汪雪元：论文初稿撰写；所有作者都对本研究的概念和设计做出了贡献、对最终稿的前几个版本进行了评论、都阅读并同意了最终稿。