一种基于点面特征的低漂移视觉里程计

金 犇，贝绍轶，尹明锋，李凌岩

(江苏理工学院， 江苏 常州 213000)

0 引言

视觉里程计(visual odometry，VO)旨在根据周围环境信息估计出相机在未知环境中的运动位姿，被广泛运用于无人驾驶、移动机器人、虚拟现实(VR)、增强现实(AR)等领域。

基于特征的视觉里程计主要跟踪连续帧之间的特征，并最小化重投影误差来估计相机的运动。在长走廊、白墙等低纹理环境下，PTAM、ORB-SLAM2等[1]基于点特征的开源视觉里程计算法，无法有效跟踪特征点，导致算法精度和鲁棒性很差。针对这一问题，边缘、线、面等具有更强鲁棒性的高维特征被广泛使用。Gomez-Ojeda等[2]在SVO[3]框架上提出基于双目相机的视觉里程计PL-SVO，其思路是检测图像中的LSD线特征并进行匹配，基于光度不变假设最小化各点与重投影点之间的光度误差，计算相机位姿。孙沁璇等[4]提出了一种基于平面直线特征的视觉里程计，充分考虑平面与平面、平面与直线之间的几何关系，以及特征之间的关联。Kim等[5]提出了一种利用室内场景结构的无旋转漂移的视觉里程计OPVO，通过计算环境的曼哈顿主方向来确定相机的绝对无漂移方向，通过深度信息最小化跟踪点的去旋转重投影误差，找到最优平移。LPVO[6-8]在OPVO的基础上联合RGB图中的线特征和深度图中的表面法向量来稳定识别环境的正交结构，防止未识别到两个及以上的平面造成跟踪丢失的情况。Li等[9-10]提出了一种融合点线面特征的PlanarSLAM，考虑了曼哈顿主方向丢失的情况下，利用点线面联合误差函数计算旋转和平移，增强了在弱结构环境下的鲁棒性。

综合分析上述算法，根据曼哈顿世界(Manhattan world，MW)假说[11]计算的是一种低漂移旋转矩阵。进一步考虑对MW假说下低漂移旋转矩阵的利用，提出一种基于点面特征的低漂移视觉里程计方法。该方法在ORB-SLAM2框架基础上，将通过MW假说计算的旋转矩阵与点面特征联合重投影误差函数计算的变换矩阵进行关联，在提高精度的基础上消除累计误差，提高系统的鲁棒性。

1 算法框架

基于点面特征的低漂移视觉里程计的工作流程如图1所示，分为3个主要模块，特征匹配模块、曼哈顿主方向计算模块、相机位姿估计模块。

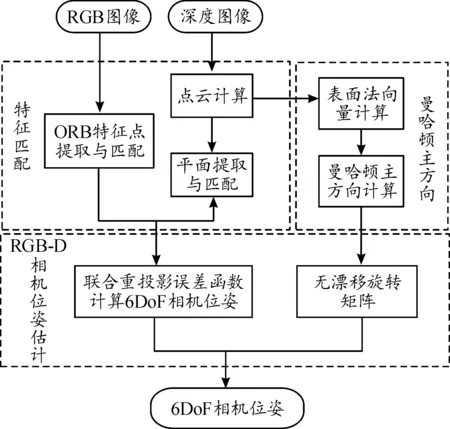
图1 低漂移视觉里程计工作流程框图

在特征匹配模块中，根据当前帧的RGB图像提取并筛选ORB特征点，构成点特征集；根据时间戳上对齐的深度图计算点云，提取平面特征，构成平面特征集。在曼哈顿主方向计算模块中，将根据点云计算得到的表面法向量，投影到上一帧的曼哈顿主方向上，计算当前帧的曼哈顿主方向。在相机位姿估计模块中，根据提取的点特征集和平面特征集构建联合重投影误差函数，利用高斯牛顿法进行迭代优化，求出当前相机的位姿。分别计算前后两帧的曼哈顿主方向，通过相机坐标系与曼哈顿主方向之间的变换计算得到低漂移旋转矩阵。将联合重投影误差函数计算的6DoF相机位姿中的旋转矩阵和低漂移旋转矩阵进行关联，得到当前新的6DoF相机位姿。

2 位姿计算

2.1 点特征提取

视觉里程计中点特征采用ORB[12]特征(图2)，ORB特征由改进的Oriented FAST角点和BRIEF描述子组成，点特征的二维坐标用pi=(ui,vi)表示，三维坐标用Pi=(Xi,Yi,Zi)表示。

图2 ORB特征点示意图

2.2 平面特征提取

平面使用AHC方法[13]提取(图3)。相比较RANSAC、基于法向信息的区域生长平面分割等平面提取算法，AHC方法精度高且能满足实时性需求，在640×480分辨率的情况下可达到35帧。将提取出的平面参数用π=(nπ,d)表示，其中nπ=(nx,ny,nz)表示平面的法向量，d是相机坐标原点到平面的垂直距离。

图3 AHC平面提取示意图

2.3 曼哈顿主方向计算

MW假说假定城市场景中具有3个相互正交的主方向形成的坐标系，建筑平面的法向量与坐标轴的其中一个主方向保持平行(见图4)。对于服从MW假说的结构，表面法向量ni在单位球S2(S2表示三维欧氏空间R3中的单位球面)上是一个有组织的分布，可以用于识别曼哈顿主方向。可以合理地假设表面法向量ni是一个概率密度函数的样本，它们更有可能分布在MW的主轴上。因此，寻找主轴的过程等价于在这个概率密度分布函数中寻找局部极大值。

图4 曼哈顿主方向

表面法向量ni[14]通过计算2个与点Pi所在局部曲面相切的向量以及计算两个切向量的叉积得到点Pi的法向量，由于深度数据存在噪声以及易丢失等问题，用积分图像的方法对切向量进行平滑。用提取的法向量计算曼哈顿主方向[15]，具体算法流程如算法1所示。

算法1曼哈顿主方向计算

输入：表面法向量ni

输出：旋转矩阵Rci,m

1. for inter=1:NUM

2. fori=1∶3

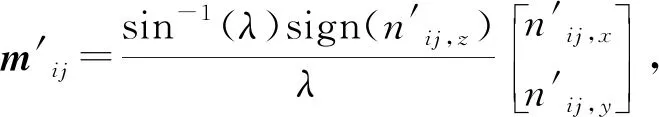
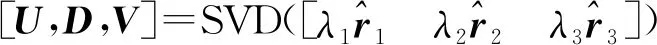
10.Rci,m=UVT

11. end for

12.end for

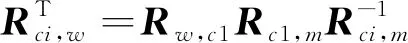
(1)

其中:Rw,c1是相机与世界坐标系之间的旋转矩阵，其初始值为单位矩阵；Rc1,m在初始化时计算得到：

(2)

相机的旋转矩阵Rci,c(i+1)由前后两关键帧的相机与曼哈顿主方向的旋转计算得到：

(3)

2.4 点面特征联合误差函数计算位姿

在一些特殊的环境中(如图5所示)，初始帧为单一平面，无法计算曼哈顿主方向，利用上文中提取的ORB特征和平面特征构建联合重投影误差函数。

图5 TUM RGB-D数据集 Fr3-n-t-f和Fr3-n-nf

将特征点的三维坐标Pj按照当前估计的位姿投影得到的位置与该点的像素坐标pk做差，得到如下的重投影误差：

(4)

其中δ是投影函数。

平面进一步用q(π)=(φ,ψ,d) 表示，其中φ=arctan(ny/nx)，ψ=arcsin(nz)。平面之间的相似度匹配先比较两平面的法向量的夹角，是否低于阈值9°；再比较坐标原点到平面的距离是否小于阈值8 cm；如果两者皆满足则判定2个平面相似。

观测平面πk和对应的平面πj构建如下的平面特征误差函数：

(5)

根据式(4)(5)构建如下的点面特征联合重投影误差函数：

(6)

其中:Λpk, j、Λπk, j是点、平面的协方差矩阵，ρp、ρπ是鲁棒核函数，最终用高斯牛顿法迭代优化出当前相机位姿[R,t]。

在位姿估计中，充分考虑了特征之间的关联，对于上文用平面特征计算得到的曼哈顿世界主方向进行充分利用。

当前帧未检测到场景的曼哈顿主方向，则用式(6)计算得到的[R,t]作为变换矩阵。

若当前帧中检测到曼哈顿主方向，则根据检测到的正交平面的数量进行计算。通过计算相机与曼哈顿主方向之间的旋转来计算相机前后之间的旋转，是一种低累计漂移误差的旋转矩阵计算方式。利用这种计算方式可以有效地消除累计的漂移误差。对最终的旋转矩阵Rnew进行计算，具体计算公式如下：

(7)

其中:nπ为正交平面的个数，nt为每十帧中检测到的曼哈顿主方向的帧数。

3 实验以及算法评估

为了验证本文算法的有效性，在合成数据集ICL-NUIM[16]和真实世界数据集TUM RGB-D[17]上进行算法精度测试。

为了评价算法估计轨迹的效果，用相对位姿误差(relative pose error，RPE)[18]的均方根误差(root-mean-squared error，RMSE)值来量化算法的精度，相比较绝对轨迹误差(absolute trajectory error，ATE)，RPE更适合用来评估视觉里程计算法的漂移程度。

(8)

运行环境的电脑具体配置如下：CPU为Intel(R) Core(TM) i7-9750H CPU、主频2.60 GHz、内存8 GB、显卡为NAIDIA GeForce GTX1650、系统版本为Ubuntu 16.04 LTS 64位+ROS Kinetic。

3.1 ICL-NUIM数据集定位结果与分析

ICL-NUIM数据集是由客厅和办公室序列组成，其中合成的RGB和深度图像是在虚拟环境中以30 Hz频率捕获，通常用于评估三维重构以及SLAM算法。为了进行算法的性能评估，将本文算法与ORB-SLAM2、OPVO算法在合成数据集ICL-NUIM上进行测试。

如图6所示，本文算法轨迹与数据集真实轨迹基本相符。表1中RPE的RMSE值和最大值(MAX)数据表明，相较于ORB-SLAM2、OPVO算法，本文算法在大部分序列中的轨迹与真实轨迹的RPE更小。这是因为ICL-NUIM数据集图片中多为白色沙发、墙面、木桌等缺乏纹理物体，ORB-SLAM2算法无法提取足够的特征点进行跟踪，使得RPE的RMSE值较大；而OPVO利用平面的正交性解算旋转和平移，没有关键帧选择以及闭环检测机制来降低累计漂移误差，导致精度较低。与ORB-SLAM2和OPVO算法相比，本文算法在弱纹理的环境中能够有效利用环境正交平面等结构信息对相机位姿进行不断修正，在弱纹理的结构环境中精度更高。

表1 各算法在ICL-NUIM数据集上运行轨迹的RPE数据 m·s-1

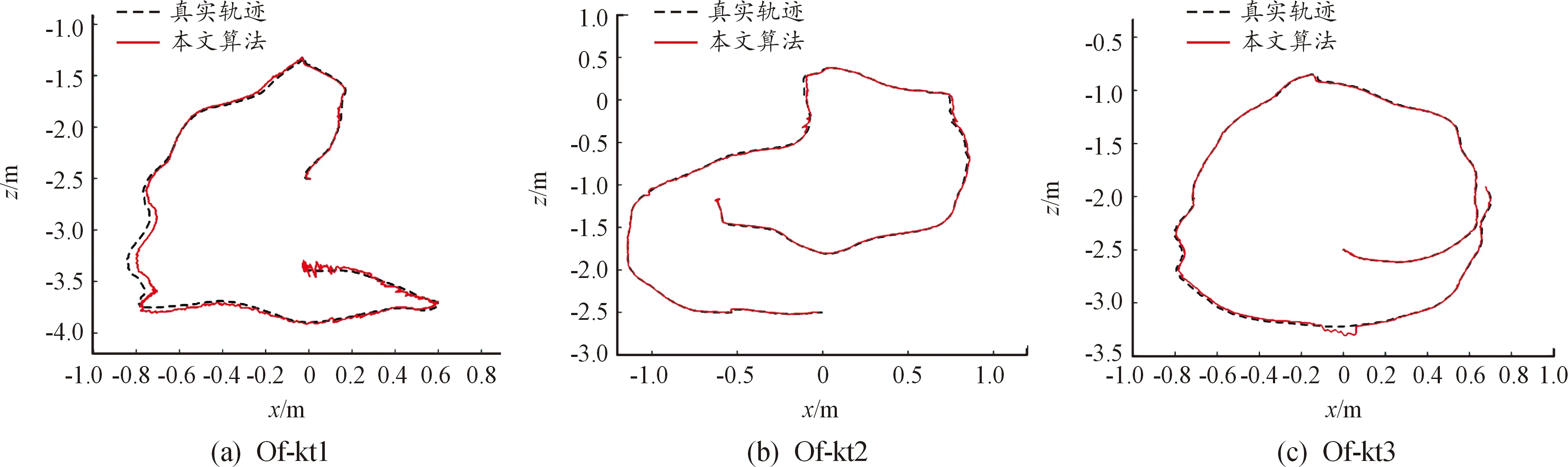
图6 本文算法在ICL-NUIM数据集上估计的相机轨迹

具体运行数据如表2所示，其中加粗数字为评测算法在该数据集中的最优数据，-表示该算法在当前数据集无法运行。

表2 各算法在TUM RGB-D数据集上运行轨迹的RPE数据 m·s-1

3.2 TUM RGB-D数据集定位结果与分析

TUM RGB-D数据集是慕尼黑工业大学著名VO/V-SLAM评估数据集，包含了在各种室内环境中用微软Kinect RGB-D相机采集的RGB-D图像。本文算法在TUM RGB-D数据集上与ORB-SLAM2、OPVO、LPVO等算法做对比分析。

从表2RPE的RMSE数据和图7的直方图可以明显看出在本文算法在大多数序列下有着更高的精度。

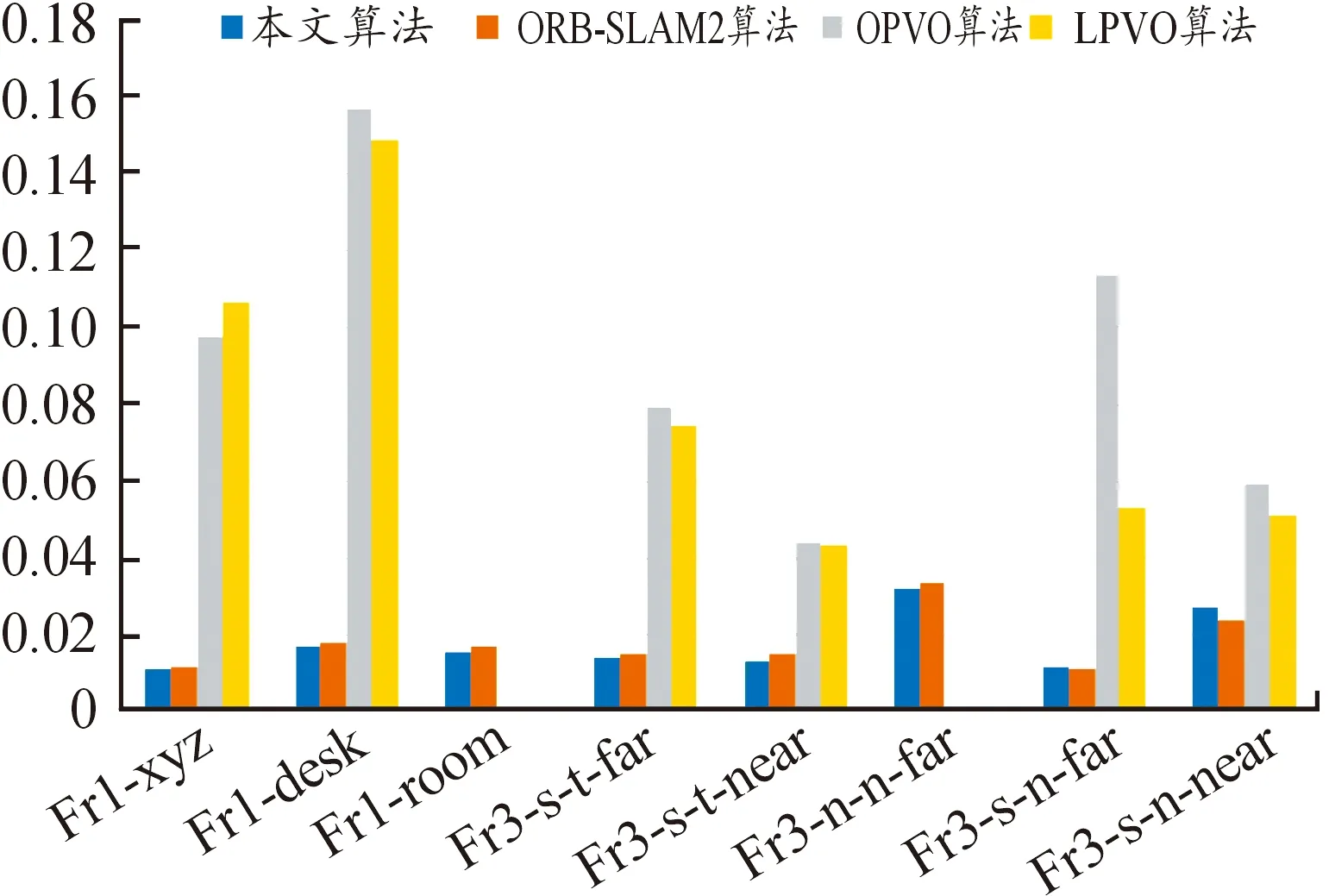
图7 各算法在TUM RGB-D数据集上的RMSE值直方图

在Fr3-s-t-far和Fr3-s-t-near这2个具有很强结构性的序列中，相比于ORB-SLAM2算法，本文算法的精度提高了8.47%和10.59%，而在Fr1-desk、Fr1-room、Fr3-n-n-far等序列下分别提高了7.61%、7.60%、3.57%，提高较多。在结构环境中曼哈顿主方向计算得到的相机旋转矩阵比较可靠。OPVO和LPVO算法在Fr1-room和Fr3-n-n-far序列下，因为序列第一帧为单一平面，无法完成初始化，程序无法运行。LPVO算法在OPVO算法的基础上加入了线特征来稳定识别环境中的正交结构，在大多数序列下精度要高于OPVO算法。

由图8(a)中轨迹可知，ORB-SLAM2算法在轨迹的最下方以及右上方的转角处发生了较大偏移，而本文算法轨迹在转角处较真实轨迹无较大偏差，说明在强旋转的情况下，本文算法的精度和鲁棒性更优秀。据图中整体轨迹分析，本文算法的轨迹明显更为平滑，波动更小。在图8(b)中，本文算法以及ORB-SLAM2算法在相机运动轨迹较为平缓的序列下，估计轨迹与真实轨迹十分接近。

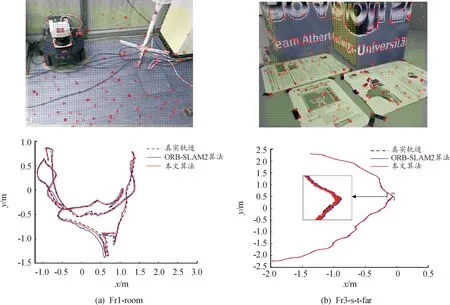
图8 本文算法以及ORB-SLAM2算法在TUM RGB-D数据集上估计的相机轨迹

由图9可以明显看出，在Fr1-room序列，ORB-SLAM2算法总体的RPE偏差值比本文算法高，与表2中的数据相符合。其中ORB-SLAM2算法在第598帧出现了最大RPE偏差值0.135 7。598帧所对应的图片中背景为白色桌面，图片中物体都较为模糊，缺乏纹理提取点特征进行跟踪。

图9 各算法在Fr1-room序列上的RPE偏差值曲线

由图10可以看出，在x轴上600～800帧，由于当前序列图片环境中的弱结构性，本文算法与真实轨迹存在较大偏差；而在z轴以及欧拉角上的偏差，因为对旋转矩阵进行了自适应加权，由MW假说计算的帧间旋转有效地降低了由联合误差函数计算位姿的累计漂移误差，两者的加权降低了出现较大偏差的可能性，进一步增强了在弱纹理环境下的鲁棒性。相较于ORB-SLAM2算法，本文算法的轨迹波动更小。

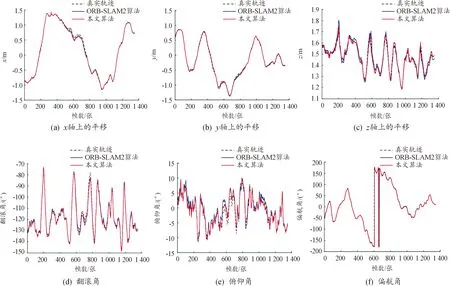
图10 各算法在Fr1-room序列上的参数曲线

4 结论

针对传统视觉里程计在室内弱纹理环境中定位精度差等问题，提出一种基于点面特征的低漂移视觉里程计。充分利用点面特征以及环境结构信息，设计自适应权重对旋转矩阵进行优化，并在合成数据集ICL-NUIM和真实数据集TUM RGB-D上分别进行测试，从相机轨迹以及6DoF上偏差等多重角度进行分析，结果表明本文算法因加入曼哈顿主方向计算的旋转矩阵，而在弱纹理环、结构化环境中具有更高的定位精度。