一种快速的无人机载侦察雷达航迹相关方法
2022-07-22高一栋党腾飞
牟 聪 高一栋 王 伟 党腾飞
(西安电子工程研究所 西安 710100)
0 引言
强杂波复杂环境下的多目标跟踪航迹相关问题一直是多目标跟踪领域研究的热点,也是多目标跟踪领域的核心问题。对于具备对地探测的无人机载侦察雷达系统,点迹数量会随着探测距离的增加近似成平方倍的增长,随着点迹的增加,航迹与点迹相关的计算量会出现急剧的增长,当点迹数量较多时会占用大部分的处理时间,这是导致计算量猛增的最重要的原因,计算量的增加与处理周期有限之间会出现不可避免的矛盾,采用基于分区的相关方法会避免航迹与无关点迹是否相关的判断与运算,从而大幅度降低计算量,降低对硬件的要求,提升雷达的处理能力和航迹输出能力。
1 应用背景
无人机载侦察雷达搭载无人机升空,可以对较远区域的敌防区实施大擦地角侦察,提高地面目标的可见度。无人机执行任务机动灵活、长航时和使用代价小,可以深入敌方前沿纵深,克服星载侦察系统实时性差的不足,提升地面目标探测的实时性,使之成为星载侦察系统的有效辅助侦察系统。雷达可不受制约地在烟雾、灰尘和其它人工遮挡物等条件下全天候、全方位、全天时工作。雷达与无人机平台结合后具有环境适应性强和信息获取实时、有效、精确、持续等优势,可以满足我军远程精确打击对火力分配所需的战场态势感知信息、火力打击所需的高精度目标指示信息、打击效果评估所需高分辨图像信息的需求,成为远程精确打击的重要传感器,例如美军全球鹰无人机加装机载侦察雷达后具备全天候的广域侦察能力。
对地探测作为无人机载侦察雷达的一个重要功能,要求雷达的数据处理系统能够尽可能多地处理大角度、大距离范围的回波点迹,因此如何解决点迹数量增加所导致计算量急剧增加问题成为影响无人机载雷达处理能力和目标航迹输出能力最关键的因素。解决此问题可以显著地降低海量点迹条件下的计算量,降低对硬件的要求和成本。
现在的航迹相关方法一般采用航迹库中的所有航迹与点迹逐个比较的方法,当符合相关条件时将点迹作为与此条航迹预相关点迹集合的成员,然后采用一定的准则将点迹与航迹之间唯一匹配,但是此类方法存在一个问题,当点迹数量较少时不太明显,但是当点迹数量较多时会使航迹库中的航迹大量增加,点迹与航迹库相关时计算量的猛增,导致下一周期数据到来时上一周期的数据还未处理完而无法完成对地探测。
相关文献针对航迹关联降低运算量和提升实时性进行了一定的研究,如朱嘉提出了一种新的多目标快速数据关联算法,周航提出了一种采用网络概率的多目标航迹相关算法,提高了正确性,占用时间较短。但以上方法均停留在理论仿真层面,且无法避免点迹和航迹数量增多导致的遍历比较所带来的计算量爆炸问题。
本方法采用一种基于分区处理的思想来进行航迹相关,解决无人机载侦察雷达对地探测中点迹增多所导致的计算量急剧增加问题,同时在航迹相关提出了一种基于运动状态判断的航迹关联方法,在几乎不增加计算量的情况下,进一步提升航迹相关的正确率,提升航迹处理的精度。
2 方法原理
2.1 算法原理说明
本算法原理概括为以下几个步骤:
1)将雷达的所有航迹和探测得到的点迹补偿至统一的以载机为原点的坐标系,即将航迹与点迹进行空间坐标对齐。
2)按照雷达的最大作用距离和最小作用距离在距离段上均分若干个距离区段,每一个距离区段大小分配原则应该与雷达探测帧周期时间长度和探测的目标最大可能速度相关,既不应该过大也不应该过小。
3)按照雷达本帧探测的最大方位范围均分为若干个方位区段,方位分区的大小分配原则与步骤(2)类似。
4)通过步骤2)与步骤3)可以得到二维平面内的若干区域块,并进行编号,然后对每一个点迹分配区域块,此步骤完成后每一个点迹都归属于一个区域块,每一个区域块都有若干个点迹归属于它。
5)对每一个航迹按照步骤4)的方法分配区域块,区域块的编号要与步骤4)的区域块的完全一致。
6)然后提取此航迹所属区域块及它周围区域块的点迹,通过基于运动状态判断的航迹相关方法进行判断,完成相关。
2.2 图例说明
1)本方法的实现总体框图如图1所示。

图1 本方法步骤框图
图1中每一个框图的步骤1~步骤6分别对应2.1部分的1)~6)。
2)划分区域块与点迹的对应关系为简单起见,假定共有15个观测区域,并将距离维划分为3个区域段,方位维划分为5个区段,示例如图2所示。
图2中区域块1到区域块15共同组成了整个探测区域,图中的•表示点迹,左上角的数字为点迹编号。
3)以图2的例子为例,建立航迹与区域块对应关系如图3所示。
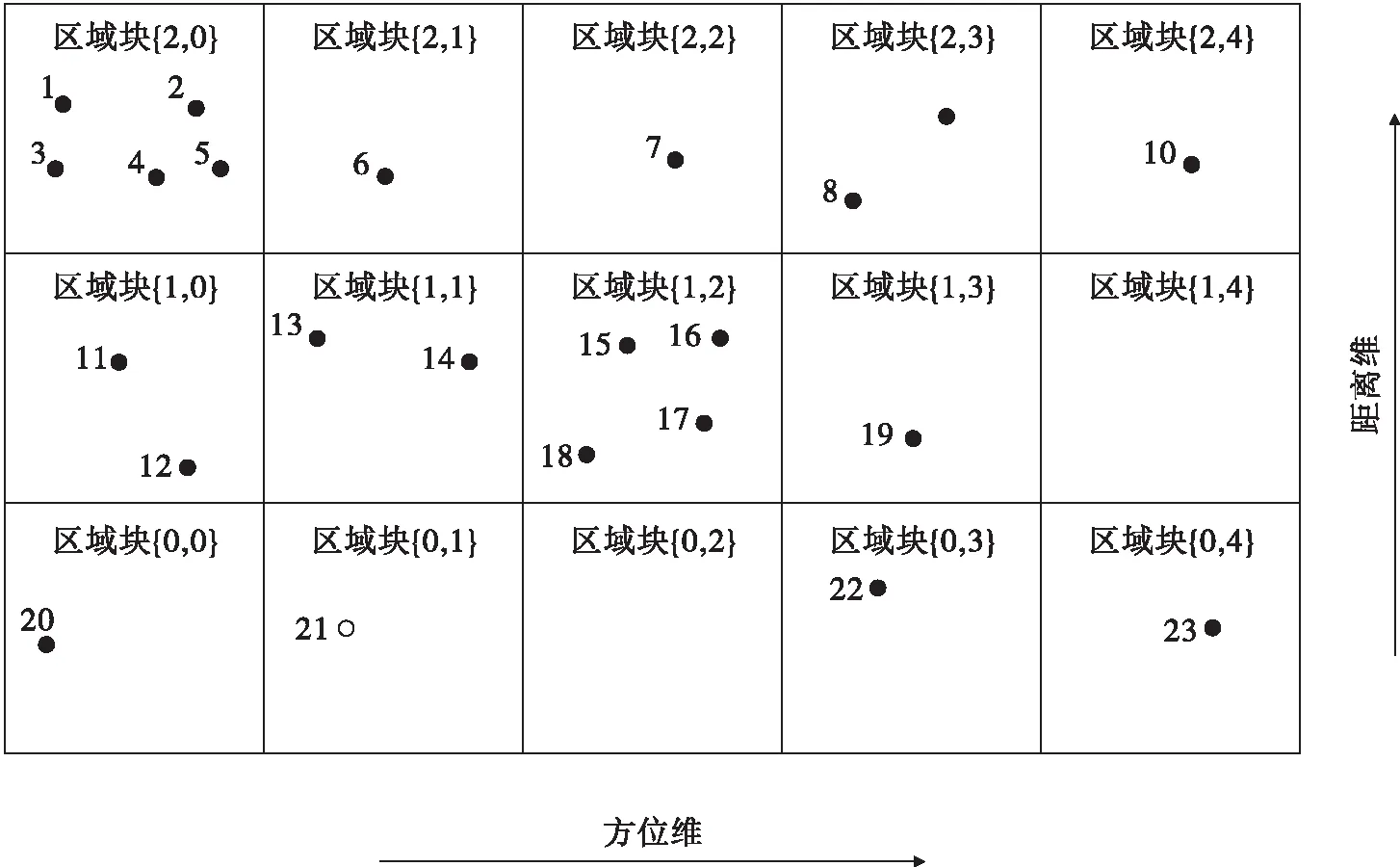
图2 点迹与区域块关系图例
图3中★表示航迹点,左上角为航迹编号,即航迹批次号。从图例说明中可以看出,每一个航迹点与点迹相关过程中只需要同本区域块临近区域块且处于航迹相关波门内部的点迹进行相关比较即可,避免与所有点迹进行相关运算,从而大幅度地降低计算量。
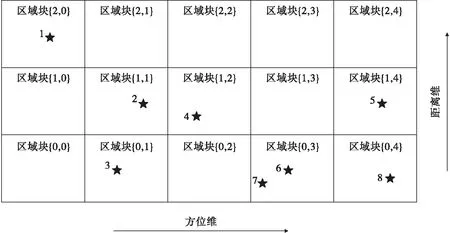
图3 航迹与区域块关系图例
2.3 航迹相关
目前比较经典的航迹相关算法主要有以下几种:
1)最近邻法(NN),即选取处于相关波门内部,距离航迹预测点最近的点迹作为航迹的更新点迹。
2)概率航迹相关(PDA),该关联方法使用所有落入波门的点,并对所有的点通过加权来获得等效点迹,采用等效点迹来进行航迹的更新,该方法数据计算量相对较小,但是在目标跟踪中落入相关波门的点迹只有一个是真实目标的回波点迹,如果采用所有回波加权势必会造成精度的降低。
3)联合概率航迹相关(JPDA),该方法是杂波环境下对多目标跟踪较好的方法,该方法考虑了航迹波门相互交叠区域有点迹的情况,但是当观测点迹密度很大且杂波比较强的情况下,该方法会引起计算量的爆炸,工程应用性不强。
目前工程中最常使用的方法为最近邻法则,本方法从考虑工程实用方面,经过对最近邻法则做适当修改,引入多普勒通道号,即同时采用距离、方位和速度构建相关波门,过滤点迹,不失一般性,采用如式(1)所示的距离和方位相关波门为
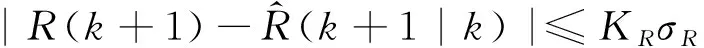
(1)
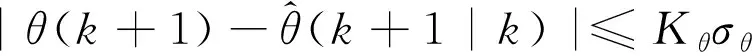
(2)
增加速度波门,由于一般的脉冲多普勒雷达上报的点迹都有多普勒通道号信息,可以结合雷达的最大可能加速度设计雷达的速度波门,计算公式如式(3)所示。
|(+1)-(+1|)|≤
(3)
式(1)、式(2)中,为距离误差,为方位误差,、为比例因子,在使用中根据实际情况进行调整,物理意义就是,方位观测值和预测值的差值不会超过倍测角误差,距离观测值和预测值的差值不会超过倍距离误差,因为在实际工程使用中预测误差是一个很难获取的量,所以在式(1)和式(2)中,、一般选取大于1的数,即其中不仅包含测量误差也包括预测误差,式(3)速度波门相关条件,(+1)、(+1|)为当前多普勒号的观测值和预测值,距离和方位的预测可以根据径向速度和切向速度结合扫描周期做两点外推确定,多普勒号的预测则考虑目标运动的加速度和扫描周期确定,可以根据历史点迹选取一定的窗长做滑窗处理,对多普勒通道号进行平滑然后根据两点外推预测当前帧的多普勒通道号,同理也为一个大于1的数。
对同时满足距离、方位和速度波门的点迹选取距离预测点最近的点迹来进行航迹的更新,如果同一回波同时落入两个航迹的相关波门,且在这两条航迹相关波门内均是距离预测点最近的点迹,则根据这两条航迹的存活时间、航迹的稳定性综合进行比较后,将该点迹用于更新航迹存活时间和航迹稳定性相对来说更合适的航迹。
3 应用案例
对于无人机载侦察雷达对地动目标侦察,主要获取目标在二维平面的实时地理位置,作为本方法的应用目标,结合在某项目中的实际使用介绍具体应用方法。
下边结合上述附图和前述的步骤详细介绍此方法的具体实施方式。
1)数据补偿。
航迹数据和本扫描周期的点迹数据采用惯导数据补偿至以载机为原点的坐标系,本例补偿至以载机为原点的地理坐标系,具体转换方法属于一般的坐标旋转和平移操作,不属于本文的主要研究内容,因此这里不再赘述。
2)划分距离区段。
距离区段的大小主要应该考虑目标的最大径向速度、距离相关波门的大小、距离分辨单元大小、雷达扫描周期等因素。
假定距离分辨大小为Δ,目标的最大速度为,扫描周期为,则距离区段参考值可以简单计算为
Δ=2·(Δ+·)
(4)
距离区段的个数为
=ceil[(-)]
(5)
其中ceil[·]为向上取整,和分别对应的最大距离和最小距离,必须大于雷达作用距离,以使点迹和航迹的距离值不可能大于此值,也必须小于雷达的盲区,以使点迹和航迹的距离值不可能小于此值,在实际的操作中,为了便于计算和尽量选择在整数公里处,选取参考式(4)的计算结果,工程实际中,可选取能被1000或100整除的值,这样方便距离区段个数计算,例如当和值分别为100km和5km时,按照式(4)计算Δ结果为86m,则可以直接选取Δ为100m,这样距离区段个数按照式(5)计算为950。
3)划分方位区段。
与距离区段的划分类似,由于无人机载侦察雷达的飞行高度达数千米,对地面目标的最近探测距离较远,一般情况下,地面目标在有限的扫描周期内不会跨越较大的方位角度,假定角度误差为,因此角度区段参考值可以简单计算如式(6)所示。
Δ=2·(·+)
(6)
角度区段个数为
=ceil[(-)Δ]
(7)
与分别为方位最大角和最小角,与距离区段划分规则类似,实际选取参考式(6)结果,选取能被-整除的最近数值,例如按照式(6)计算的Δ为22°,-为60°,则可以将置为3°,这样方位区段个数为20个。
经过实测,Δ和Δ在不太大范围内变化时,对计算时间的影响不大,因此按照参考公式计算并选择能够被距离范围和方位范围整除的距离和方位区段大小是合理的,不会影响计算结果。
4)点迹与区域块对应关系建立。
按照前述的方法对整个区域进行完距离和方位分区后,整个观测区域就划分为如图2所示的若干个矩形区域块,点迹分配至每一个区域块。
5)航迹与区域块对应关系建立。
与点迹与区域块对应关系建立方法相同,建立航迹与区域块的对应关系。
6)航迹与点迹的相关。
航迹相关时根据式(1)、式(2)形成距离和方位相关波门,、取值4,即当距离观测值和方位观测值与预测值之差分别不超过4倍的误差值,取3,落入相关波门内的点迹为候选点迹,选取与预测值空间距离最近的点迹用来更新航迹;当一个点迹同时落入两个航迹的相关波门且均是距离两个航迹预测点最近的观测点,则将其用于更新存活时间较长的那条航迹,如果这两条航迹的存活时间基本相同,则本点迹更新外推次数更少的那条航迹,另一条航迹则进行外推。
4 结果对比
以下采用某型机载侦察雷达三个架次对同一区域在正样鉴定中的实飞数据使用传统的航迹相关(航迹相关时采用最近邻法)方法和本方法分别统计100个扫描周期的平均航迹处理运算时间和处理精度,其中每一个扫描周期录取的点迹数量约6000至8000个,航迹数量约4000个左右,扫描周期为3s。
为了方便起见,采用对原始回波进行回放的方式进行对比,人为延长回放时间间隔,保证下一周期到来时上一周期的数据能够处理完毕,以便航迹处理时间和处理精度。
1)处理时间统计见表1所示。

表1 处理时间对比表
2)处理精度统计见表2、表3所示。
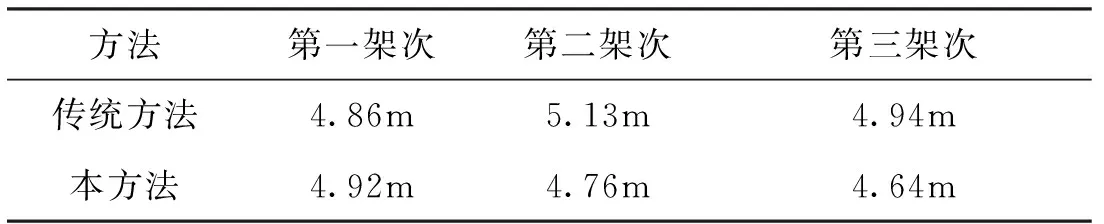
表2 距离精度对比表

表3 方位精度对比表
从表2、表3可以看出当采用传统方式时,处理时间已经超过了扫描周期,无法在下一周期数据到来时完成本扫描周期的处理,而本方法时间裕度较大,远小于扫描周期,且本方法处理时由于引入了运动速度的判断,在航迹相关时具有较高的准确性,因此在距离精度相当的情况下,角精度较高。
5 结束语
通过前述本方法的原理介绍、工程中的使用方法及步骤说明和针对实际飞行数据的不同方法之间的航迹处理时间和精度对比,可以得出如下结论:
首先,本方法在点迹与航迹相关时避免了无关点迹与航迹的比对,而是采取了近乎直接提取点迹进行相关比对的方式,省去了中间大量不必要的运算过程,提高了计算速度。
其次,本方法随着点迹数量的增加不会带来计算量的急剧增加,在相同的计算量下可以处理更多的点迹,能输出更多的目标航迹数据,能够实现对地面覆盖区域所有可检测运动目标的跟踪,成倍地提升处理能力。
最后,此方法具有较高的角精度,并且原理简单易用,大大简化了航迹相关计算量,降低了对硬件的要求,节约了成本,具有很好的推广和应用价值。
此方法已经应用于某型无人机载侦察雷达的科研试飞和定型状态鉴定,保证了机载侦察雷达的成功列装定型。
