杂波环境下强机动目标自适应关联波门选择
2020-09-02诸葛晶晶林家骏
赵 菡 诸葛晶晶 林家骏
(华东理工大学信息科学与工程学院 上海 200237)
0 引 言
关联波门的有效设定可以减少数据关联算法的运算量、提高关联精度,是数据关联算法的必要条件[1-2],通过设置波门中心为目标预测位置,实现对量测回波的筛选。概率数据关联算法(Probabilistic Data Association, PDA)[3]以及在此基础上针对多目标优化的联合概率数据关联算法(Joint Probabilistic Data Association, JPDA)[4]均是通过对波门范围内的所有回波计算概率进而加权获得目标的状态更新。因此,关联波门的选取很大程度上决定了目标的状态更新是否精确,跟踪是否稳定,乃至于是否会出现失跟。
杂波环境下的强机动目标跟踪存在目标运动状态变化情况复杂、波门中心难以预测等问题,固定波门无法应对目标在不同状态下的跟踪任务,因此研究者们相继提出了多种自适应关联波门设计方法以改善目标丢失问题,提高跟踪精度[5]。文献[6]提出了一种自适应关联波门跟踪算法,以目标发生最大机动水平作为假设,修正关联波门以增加真实回波落入概率。然而基于最大机动水平的假设使得关联波门过大,在杂波密集环境下反而会造成跟踪的不稳定甚至失跟。文献[7]同样以最大机动水平所对应的模型误差协方差对关联波门进行扩大,使得在波门内不存在有效量测时扩大波门大小以确保真实量测落入门内。然而一味地扩大波门会造成目标稳定后波门内包含过多杂波,反而影响跟踪精确度。文献[8]在误差动态变化率的提示下,根据目标飞行状态对关联波门的大小进行动态调整,有效降低了目标丢失率,提高了跟踪精度,避免了上述算法在杂波环境下的局限。然而,该方法的研究背景是选定关联波门的形状为椭圆门,仅存在椭圆门门限大小这一单一调节参数,且在跟踪强机动目标时门限调整幅度过小,容易出现失跟。文献[9]采用三种波门自适应切换的方法处理临近空间高超声速目标航迹的起始问题,一定程度上解决了上述问题中对高机动目标的跟踪问题,但并未讨论目标持续运动过程中机动变化情况下的关联波门如何切换。
综上,现有的关联波门自适应算法多为单一波门形状(通常为矩形门或椭圆门),通过估计跟踪误差来调整门限参数,实现波门大小的更新。该方法存在两大缺陷:(1) 通过跟踪误差来调整波门门限属于补救性调整,较高的滞后性导致波门更新不及时,在目标出现剧烈运动时容易失跟;(2) 单一形状的矩形/椭圆门在面对杂波环境下的强机动目标时,并不能很好地契合目标运动状态,波门中心的剧烈变化也容易导致波门内无有效量测及跟踪不稳定。
本文针对单一形状波门在跟踪强机动目标时跟踪不稳定及失跟严重的问题,提出一种自适应关联波门选择算法。通过估计当前目标的运动状态,结合目标不确定度预测失跟概率,自适应切换椭圆门、扇形门及环形门三种波门形状,并动态更新门限参数以提高波门内正确量测的关联概率。仿真结果表明,在强机动目标跟踪中,本文算法可有效跟踪目标,降低目标丢失率的同时提升目标的跟踪精度。
1 自适应参数
1.1 关联波门
面对强机动目标的复杂运动状态,采用何种关联波门进行目标跟踪直接影响真实回波的落入概率,进而影响目标的丢失率及跟踪精度。目前较常用的关联波门有三种,分别为椭圆门、环形门及截尾扇形门。

v′c(k+1)S-1(k+1)vc(k+ 1)≤γ
(1)

二维情况下的椭圆门面积为:
(2)
归一化新息协方差标准差后可得椭圆门的面积为:
(3)
(2) 环形门。与椭圆门不同,环形门与方向无关,能够捕获未知目标或启动目标,其门限参数只与目标速度相关。环形门的关联方程如下:
(4)
式中:(x,y)为回波位置;(x1,y1)为波门中心位置;R1=f(vmin)为目标的最小速度确定环的内半径;R2=f(vmax)为目标的最大速度确定环的外半径。
环形门的面积公式为:
(5)
(3) 截尾扇形门。截尾扇形关联波门是扇形门的一种,本文默认扇形门为截尾扇形门,其关联方程为:
(6)
(7)
式中:最大半径与最小半径的选取与环形门一致;增加角度限制于θ1~θ2,θ1、θ2由目标的角速度所确定。
扇形门的面积公式为:
(8)
1.2 不确定度
目标飞行过程的不确定度一定程度上反映了目标的跟踪稳定性及失跟概率,当目标不确定度过低时,说明跟踪极不稳定,应及时修正门限参数或更换波门形状。本文通过计算目标跟踪不确定度,估计目标失跟趋势,从而及时更新波门以降低失跟率。选取Hellinger距离作为衡量目标航迹预测不确定度指标。Hellinger距离通过评估量测向量与状态向量两个分布之间的一致性来判断目标的关联性能[11]。
记组合量测向量分布f=N(Zt(k),Σx),Zt(k)为组合量测,Σx代表量测向量的不确定度。Zt(k)为由关联波门确定的k时刻落入门内的mk个有效量测,其计算公式如下:
(9)

采用无偏最小方差估计迭代获得量测向量协方差的Cramer-Rao下界[12],即不确定度Σx(k|k)。
Σx(k|k-1)=F(k-1)Σx(k-
1|k-1)F(k-1)T+Q(k-1)
(10)
Σx(k|k)=Σx(k|k-1)-K(k)S(k)K(k)T
(11)
式中:F(k)为状态转移矩阵;Q(k)为过程噪声的协方差;目标增益矩阵和新息协方差矩阵分别用K(k)和S(k)表示。
用Σx和Σy分别表示量测状态向量x和估计状态向量y所对应的误差协方差矩阵,则Hellinger距离dKG(k)为:
(12)

(13)
2 算法设计
2.1 选择原理
在实际应用中,不同场景下采用的关联波门应根据实际情况调整。面对初始捕获阶段的众多自由点迹,需采用较大的无方向性波门,环形门是一个合适的选择。跟踪开始后,对于不同的跟踪目标通常有不同的波门选择策略。例如,在民用航空雷达应用中,民航机一般不会进行较大幅度的机动,因此,选择一个较小的波门即可,可以采用椭圆门,对一个速度稳定,方向变化小的目标进行跟踪。而在军用领域,由于战斗机往往速度较快,且频繁地进行紧急避让、急转、加速、减速等强机动变化,因此该场景下往往需要一个较大的波门(扇形波门/环形门)以涵盖可能出现的速度及方向变化。
尽管波门越大,越容易捕获真实目标回波,但与此同时,也会有较多来自非本目标的回波及杂波落入波门;反之,波门选取过小,会使来自本目标的回波被排除在外,产生不稳定的跟踪,甚至使得跟踪目标丢失。因此,需要根据实际情况选取恰当的波门,即不可盲目增大波门,也需要使波门大小在一定限度之内,确保目标真实回波在波门外的概率小于一定程度。
本文所采用的椭圆门、扇形门及环形门示意图如图1所示。

图1 关联波门示意图
图中,Pi-1为上一时刻预测点迹,Pi为当前时刻预测点迹,Zi+1为下一时刻的量测点迹。合适的波门应该在各种情况下都能涵盖Zi+1点。可以看出:椭圆门面积最小,但方向性最佳,适用于小机动情况,可有效减少波门内所包含的杂波;扇形波门面积次之,具有一定方向性,适用于大机动情况;环形门无方向性,波门面积最大,适用于目标启动状态及失跟时用于重新捕获目标。
2.2 选择流程
自适应波门决策主要是根据当前波门内的有效量测来选择对应波门。如前文所述,椭圆门适用于弱机动环境,扇形波门适用于角度变化在一定范围内的机动目标,环形门适用于目标丢失需重新捕获的情况。考虑单一形状波门无法应对复杂的机动环境,现提出一种自适应波门决策算法,针对不同的机动环境下的跟踪目标选择最合适的波门形状。在目标实际航行过程中,通过估计目标运动状态以及判断波门内有无有效回波来决定是否更换波门,具体的决策过程如下:
首先预测当前目标运动状态,当在波门内寻找到有效量测,根据数据关联算法得到当前目标预测速度vP(k)为:
(14)
式中:k为当前时刻;XP为预测的航迹;t为量测间隔时间。
定义δ为表示目标触发启动状态的阈值,θ为根据工程经验选取的阈值。当vP(k)<δ时,认为目标处于启动状态,则采用内半径为0,外半径为初始设定最大速度Vmax的环形门(圆形门),寻找起始航迹。
当目标|vP(k)-vP(k-1)|<δ且|atan2(vP(k))-atan2(vP(k-1))|<θ时,认为目标接近于匀速直线运动状态:更换椭圆门对目标进行跟踪。
当目标|atan2(vP(k))-atan2(vP(k-1))|>θ时,认为目标处于转弯机动状态,则更换扇形门对目标进行跟踪。
当波门内不存在有效量测或不确定度过大时,认为目标已丢失,采用默认环形门重新确定目标航迹。
此外,算法根据当前运动状态实时更新三种波门门限参数,以降低杂波落入的概率,提高真实回波在波门内的关联概率。波门门限的更新规则如下:
环形门门限参数更新规则:最小速度为max(vP-aline·t-δ,0),最大速度为vP+aline·t+δ。其中aline由跟踪目标最大线加速度所决定,留有一定的余量以防止受量测误差及预测误差影响而超出上下边界。
扇形门门限参数更新规则:最小速度与最大速度的设定与环形门一致。扇形门的顺时针转角与逆时针转角边界为±(αθ×atan2(vP(k))-atan2(vP(k-1))+δ)。其中αθ由跟踪目标最大角加速度所决定。
自适应关联波门决策算法流程如图2所示。
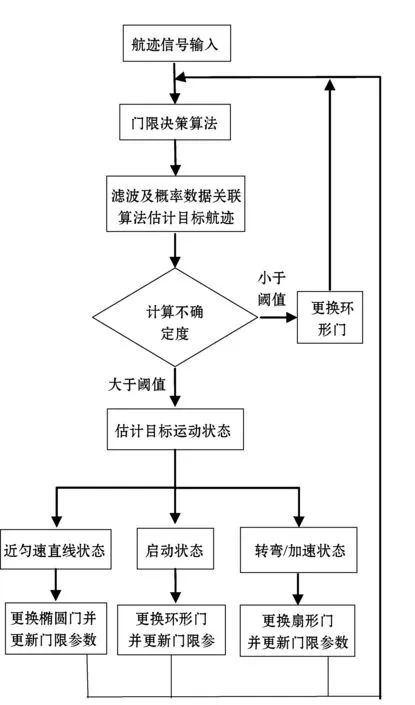
图2 自适应关联波门决策算法流程图
3 实 验
3.1 性能指标
本文采用两种机动目标跟踪性能评估指标衡量跟踪状态的稳定性及跟踪精度。采用真实回波关联概率衡量跟踪算法稳定性[13]。假设系统的状态和噪声g(k)均表现为高斯过程,则新息向量也是高斯过程,并且g(k)服从自由度为M的χ2分布。新息向量v(k)的高斯概率密度函数为:
(15)
式中:|S(k)|为新息向量协方差矩阵的行列式;M为观测维数,本文取M=2。
对于PDA算法而言,过大的门限将引入过多的杂波,而PDA算法将每一个杂波都纳入最终目标状态预测的计算中,过多的杂波在导致算法计算量增大的同时降低了正确回波的关联概率,从而影响目标状态的预测精度。相反,门限过小则增加了波门内丢失正确回波的概率。若波门内检测不到观测回波,在持续数个观测周期后算法将停止跟踪该目标,进而造成目标航迹的不连续,甚至目标的丢失。根据PDA算法定义,目标状态的更新由波门内所包含的各个回波各自加权后的和所决定。由此,可以定义波门内正确回波的归一化关联概率大小来表征门限决策算法的性能,具体数学表达式如下:
(16)
式中:第k个扫描周期内落入关联波门内的回波点迹总数为mk;vc(k)表示正确回波的新息向量。当正确回波均未落入关联波门时,其对应的归一化关联概率ωc的大小为0;若落入关联波门内的仅有正确回波,则ωc的大小为1,此时门限决策算法的性能最为优异。
计算真实航迹与预测航迹间的欧式距离误差,即位置均方根误差评估跟踪精度,具体计算公式如下:
(17)

3.2 仿真实验设定
设置目标检测概率,量测落入关联波门内的概率,杂波均匀分布在以正确量测为中心的正方形区域内,杂波密度为106 个/m2。对于三种候选波门,初始椭圆门门限常数为9.21,环形门与扇形门最小速度参数(最小半径)为0,最大速度为80 m/s,此外,扇形门最大偏转角为1.21 rad。
构建目标运动过程如下:目标初始位置位于[0,0]处,初始速度为0 m/s;1~10 s内目标做固定加速度为15 m/s2的匀加速直线运动;11~40 s内做匀速直线运动;41~50 s内向目标右前方做角加速度为11.46 rad/s2的转弯机动;51~70 s继续匀速直线运动;71~80 s做加速度为20 m/s2的匀加速直线运动。
3.3 实验结果分析
目标运动状态如图3所示。图中标记了实验仿真过程中各波门的切换情况,在启动状态时,采用无方向性的环形门进行跟踪;待运动状态稳定,目标处于近乎匀速直线运动时采用误差最小的椭圆门进行跟踪;当目标处于拐弯机动或加速状态时,采用扇形门进行跟踪。出现跟踪不稳定时,重新更换环形门进行跟踪。
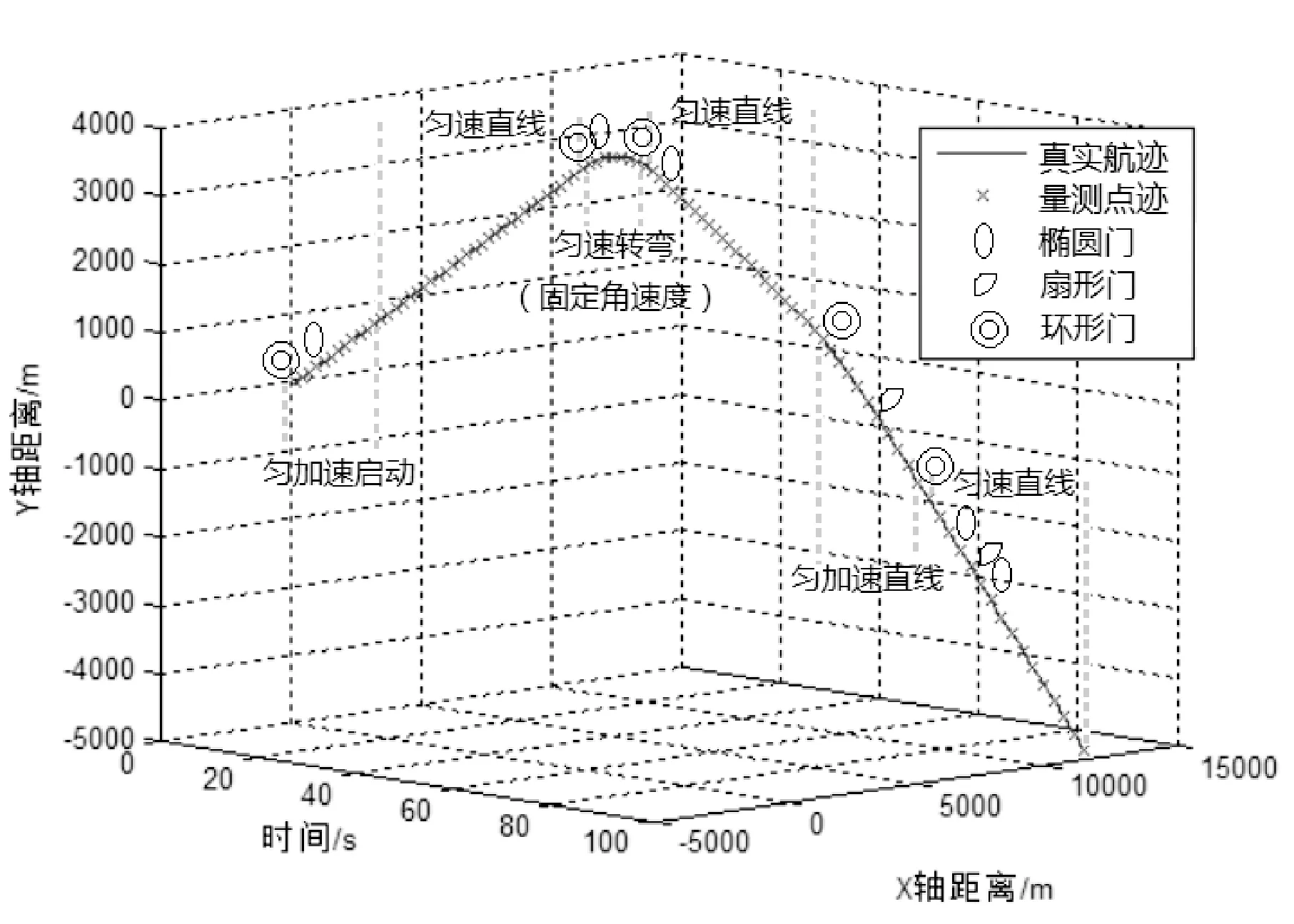
图3 目标航迹与波门切换
表1展示了波门切换情况。初始启动状态,采用了环形门,待目标稳定后,3 s开始采用椭圆门,当目标出现不稳定时,重新切换至环形门;44 s时检测到转弯机动,切换至扇形门。51 s重新采用环形门,待稳定后54 s开始采用椭圆门跟踪;75 s时目标处于加速状态,椭圆门无法跟上目标,采用环形门,确定方向后,切换至扇形门,直至检测到匀速后,83 s切换至椭圆门。随着目标的速度逐渐增大,切换至环形门、扇形门的几率也逐渐增多。目标跟踪过程的波门切换符合实际,切换过程合理。

表1 波门切换
图4展示了固定波门与本文算法在同样场景下的跟踪情况比较。起始位置处,由于扇形门是带方向性波门,对初始速度为0的目标,一旦初始方向未落在扇形门内即无法跟踪。椭圆门则在转弯机动处丢失目标,环形门在目标速度超出其初始设定值时发生丢失,而自适应波门则能根据目标当前运动状态自动切换。此外,扇形门及环形门的上下限速度及方向也能根据当前运动状态进行合理的自适应调整,因此能有效跟踪强机动状态下的目标。
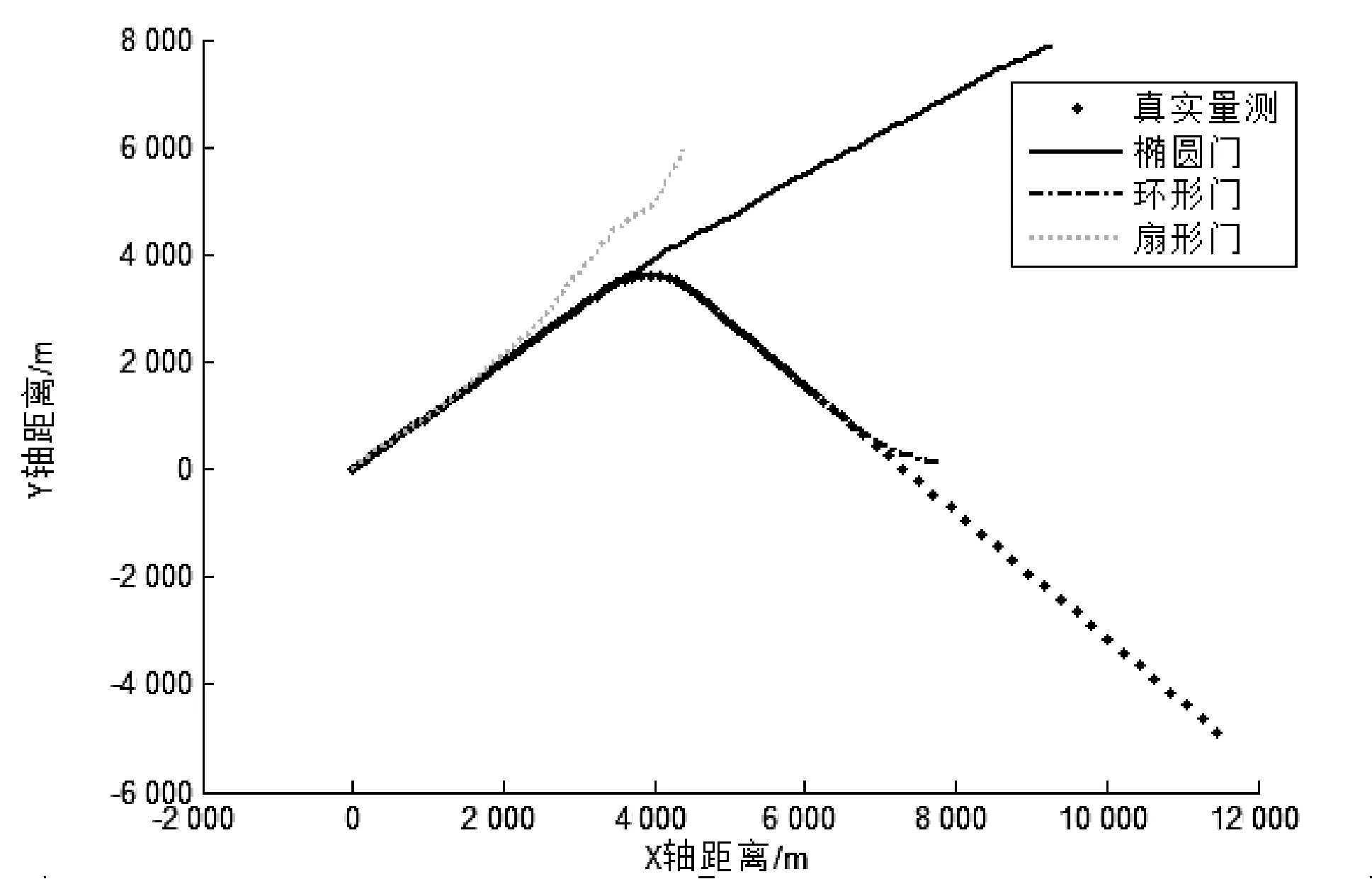
(a) 固定波门跟踪轨迹
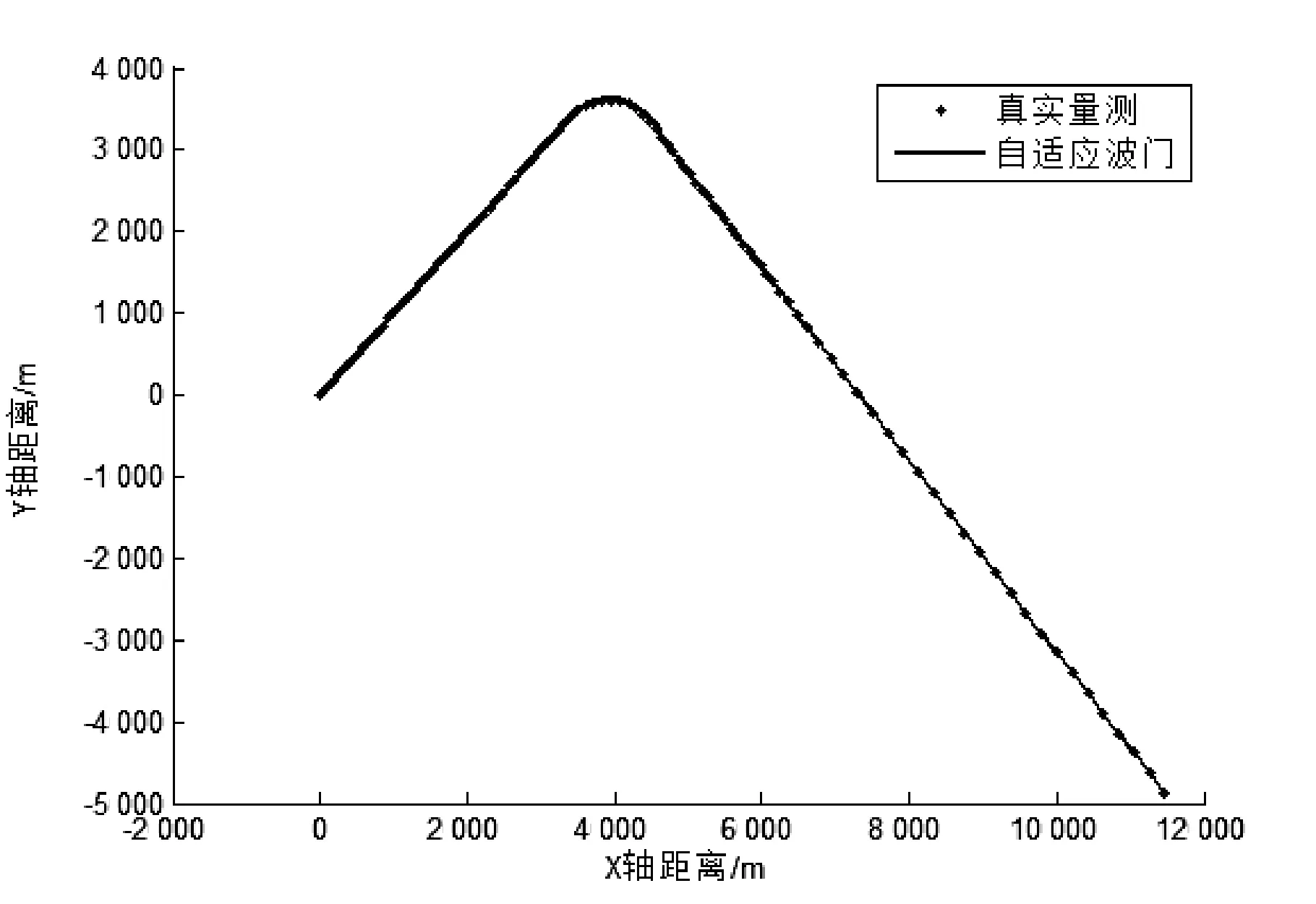
(b) 自适应波门跟踪轨迹图4 波门跟踪轨迹比较
图5展示了采用固定波门与自适应波门真实回波关联概率的对比:相比固定波门的不稳定性,自适应波门在匀速运动状态下均保持了较高的关联概率,仅在初始启动时刻、转弯机动及加速时产生一定的下降。
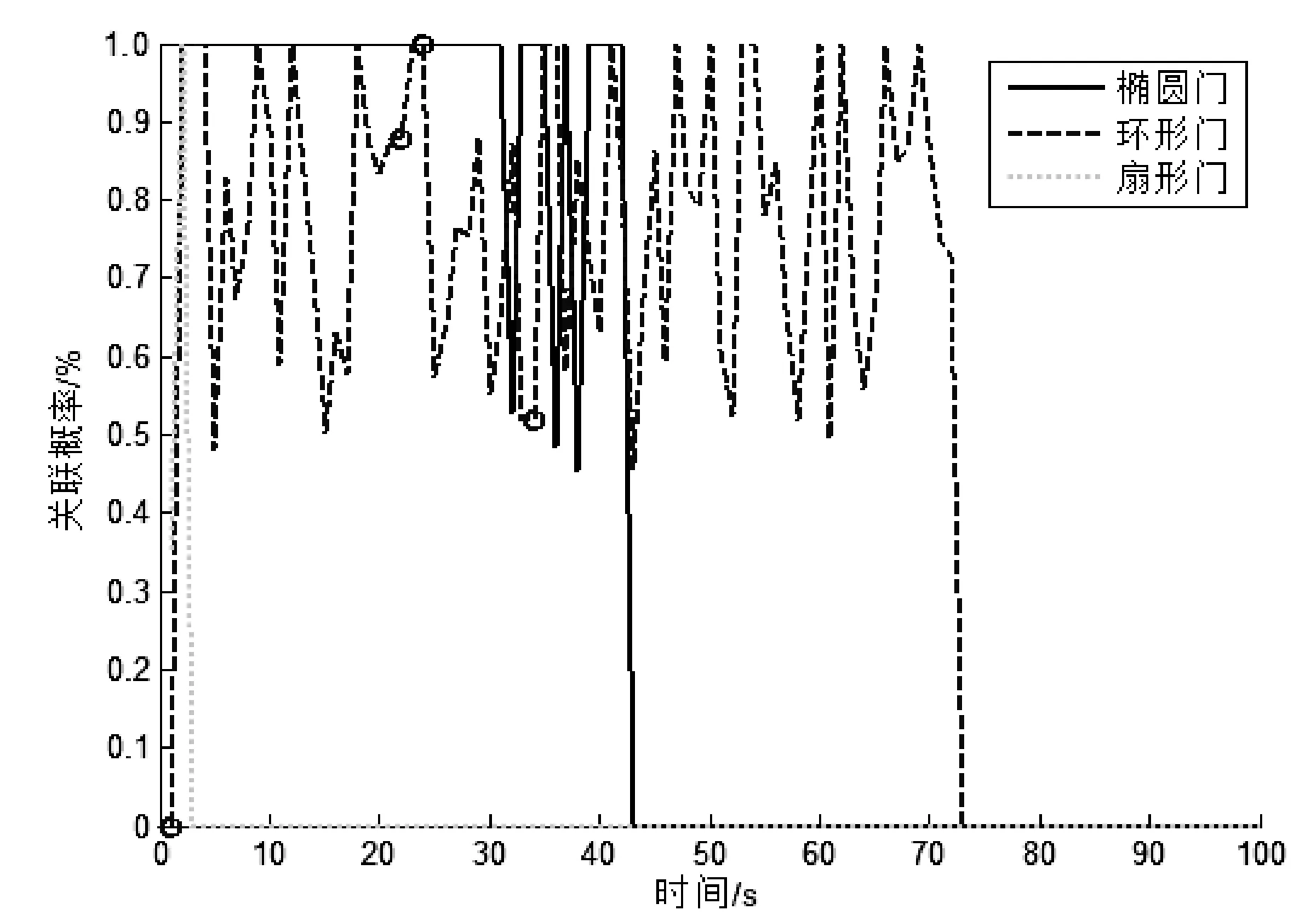
(a) 固定波门关联概率

(b) 自适应波门关联概率图5 波门关联概率比较
图6比较了固定波门与本文提出的自适应波门在跟踪精度上的性能。排除固定波门失跟情况,在跟踪过程中,本文提出的自适应波门在跟踪距离误差上亦表现出了较大程度的下降。在启动环节及匀速运动环节中,本文算法将距离误差保持在4 m以下,而在转弯与加速机动过程中,距离误差也保持在12 m以下。

(a) 固定波门距离误差

(b) 自适应波门距离误差图6 波门跟踪距离误差比较
此外,实验模拟不同杂波密度下对强机动目标跟踪性能的影响,并与文献[8]中的传统自适应关联波门算法进行了比较。比较结果如表2所示。
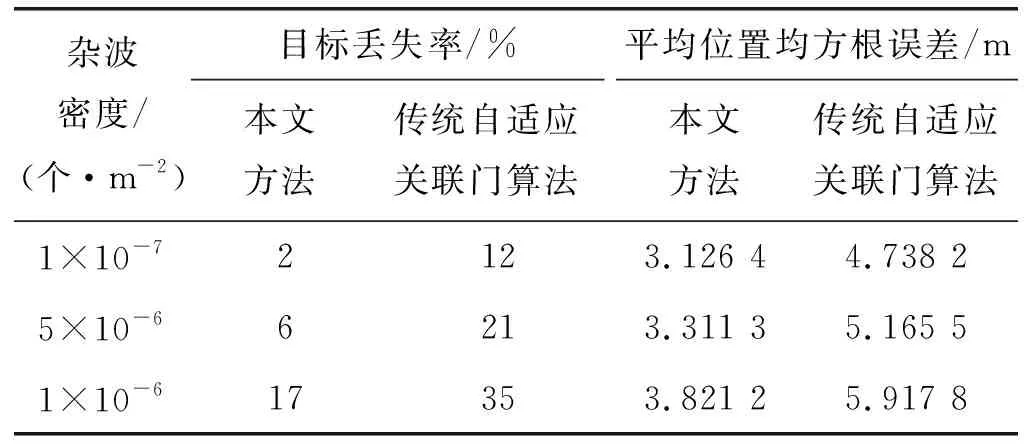
表2 不同杂波密度下两种方法的跟踪性能比较
可以看出,相比文献[8]中的自适应关联波门算法,本文算法在各杂波密度下均呈现出更低的目标丢失率及位置均方根误差,平均目标丢失率下降约15%,平均位置均方根误差下降约35%。
4 结 语
在面对杂波环境下的强机动目标跟踪问题时,固定关联波门并不能完全契合所有的目标机动状态,容易出现断跟或失跟现象。而传统的自适应关联波门设计多采用单一波门形状,在面对机动状态急剧变化且多样的目标时,容易出现跟踪不稳定乃至丢失目标的问题。本文设计了自适应波门决策算法,根据目标当前运动状态,通过动态切换椭圆门、扇形门及环形门,达到在面对不同的机动状态选择最佳波门形状,予以参与后续关联算法估计目标位置。在更新目标运动状态的同时,同步更新波门门限参数以减少波门内杂波数量。而当目标不确定度过大,预计出现失跟时,选择环形门以重新捕获目标,降低目标丢失率。实验结果表明,在不同杂波环境及不同的机动状态下,相比固定波门及传统自适应波门,本文算法都在保持较低的目标丢失率的同时获得了较高的跟踪精度。
