一种基于模糊推理的自适应关联波门设计方法

傅虹景，于守江，方 明，万亚淳

(上海航天电子技术研究所，上海 201109)

0 引言

杂波环境下的机动目标跟踪是现代雷达数据处理中亟待解决的问题，其难点在于适应目标运动状态的不确定性和消除高密度杂波的影响[1-3]。对于雷达数据处理系统而言，首先需要决策雷达量测值来源于目标还是杂波，为此引入了关联波门的概念[4]。

关联波门是用于确认量测值是否来源于目标的决策门限，它以目标的预测值为中心，用于确定目标下一时刻的量测值可能出现的范围区域[5]。如果有量测值落入波门，则这些量测值将会关联到航迹，做跟踪滤波处理。关联波门的主要作用是减少来源于杂波或虚警的虚假量测值[6-7]。如果波门门限太大，过多的量测值会落入波门内，会降低数据关联的正确率，同时增加滤波算法的计算复杂度；如果波门门限太小，由于目标运动状态的不确定性，来源于目标的真实量测值可能不会落在波门内，将直接影响到对目标的跟踪精度，甚至丢失目标[8-10]。因此，正确设置关联波门成为目标跟踪算法的重中之重[11]。

近年来，涌现出了许多关于关联波门的设计方法。基于χ2分布的椭圆波门是最简单也是应用最广的方法[12]，该方法根据目标落入波门内的概率选择波门的门限值，但是缺少自适应能力。文献[13]定义了一种双重门限方法，通过引入目标的速度和角度限制，进一步缩小波门区域，然而该方法需要关于目标的先验信息，工程应用性较弱。文献[14-15]提出了应用于交互多模型概率数据关联(IMM-PDA)算法中的扩大波门门限方法，虽然在一定程度上减少了目标发生机动时丢失目标的问题，但是并没有考虑杂波密度对波门门限的影响。

针对以上问题，在PDA算法的基础上，首先推导了关于最优波门门限的数学模型，然后基于模糊推理，提出了一种根据目标的机动性和目标所处环境杂波密度自适应调整关联波门门限的方法，从而降低了丢失目标的概率，提高了对目标的跟踪精度。

1 PDA算法

PDA算法是一种应用于杂波环境下单目标跟踪的数据关联算法[16-17]，它考虑了所有候选回波与目标相关联的情况，计算每个关联假设的似然概率，根据关联概率，将候选回波的概率加权和作为源于目标的真实回波，用于更新目标的状态估计。PDA算法框图如图1所示。

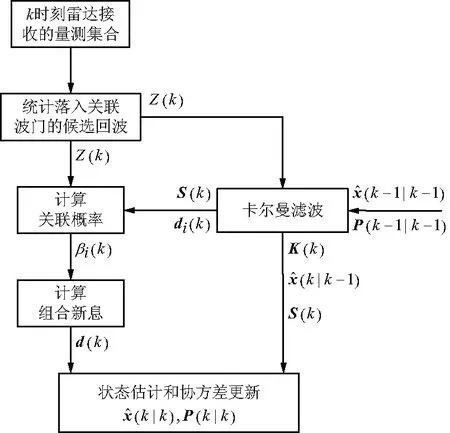
图1 概率数据关联算法框图Fig.1 Flowchart of probabilistic data association algorithm

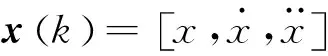
(1)

式中，G为椭圆波门门限；S(k)为新息的协方差。椭圆波门的体积可以表示为：

(2)

式中，M为量测点迹的维度；cM为与M相关的常数，特别的，c1=2，c2=π，c3=4π/3。定义候选回波集合为：

(3)

式中，zi(k)为第i个满足椭圆波门规则的候选回波；m(k)为候选回波数目。

定义βi(k)表示第i个量测点迹zi(k)来源于目标的条件概率，即关联概率，β0(k)表示没有一个量测点迹是来源于目标的真实量测值。根据关联概率加权得到组合新息：

(4)

那么目标状态的估计值：

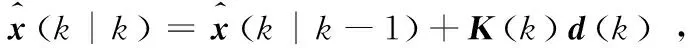
(5)

式中，K(k)为卡尔曼滤波增益。协方差的估计值：

P(k|k)=β0(k)P(k|k-1)+[1-β0(k)]×

(6)

式中，

Pc(k|k)=[I-K(k)H(k)]P(k|k-1)，

(7)

(8)

2 确定最优关联波门门限

对于机动目标跟踪问题，若目标发生较强的机动时，可能会出现关联波门内没有目标的真实量测点迹，如图2所示，传统的数据关联算法会把预测值作为状态的估计，或者关联上波门的虚假量测点迹，出现误跟现象[18]。因此，期望能够根据目标的机动性来调整关联波门，使目标的真实点迹落入波门内。同时，目标所处环境的杂波密度也会对关联波门门限有影响，所以在跟踪机动目标时，需要设立最优的关联波门来保证跟踪性能最佳。

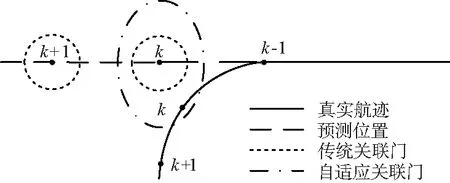
图2 目标跟踪丢失示意Fig.2 Schematic diagram of tracking target loss

最优关联波门的含义是使得源于目标的真实量测点迹zT(k)落入关联波门内，即满足式(1)的要求，同时使得波门内的虚假量测点迹数目N(k)尽可能的少。通常假设杂波的空间密度是服从泊松分布，波门内杂波数目N(k)即为：

(9)

式中，λ为杂波的密度；V(k)为椭圆波门的体积。最优波门门限的数学模型可以表示为：

(10)

根据式(10)可知，最优波门门限Gopt是随着时间变化，即具备自适应的能力，所以最优关联波门即自适应关联波门。由于目标的真实量测点迹zT(k)和杂波密度λ的时变性和不确定性，不便于直接求解最优波门门限Gopt。因此借鉴模糊逻辑的思想，根据相应的模糊规则，推理得到关联波门的门限，实现一种近似最优的自适应关联波门，其关系可以用双层映射来描述，如图3所示。

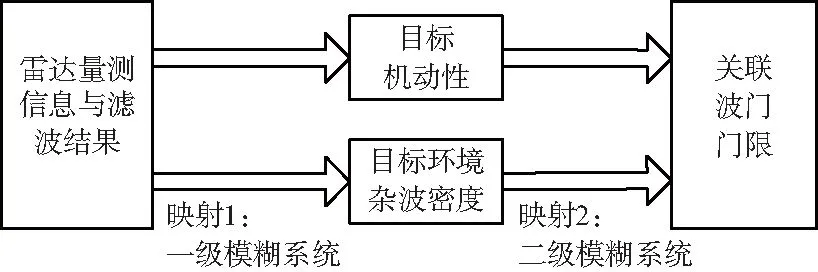
图3 模糊映射原理Fig.3 The principle of fuzzy mapping

3 基于模糊推理的自适应关联波门算法 设计

模糊推理是从一组模糊规则和已知事实中得出结论的推理过程，可以作为处理先验知识的数学工具[19]。基于模糊推理的自适应波门算法的核心思想是，从雷达的量测信息和滤波结果中提取出表征目标机动性和目标环境杂波密度的参数，并对其进行模糊化处理，作为模糊推理的输入，然后根据模糊规则得到输出结果，将输出结果去模糊化可以得到关联波门的门限，算法的具体流程如图4所示。

步骤1：确定输入、输出量并模糊化

在PDA算法中，往往采用假设目标运动模型来描述目标的运动方式，模型中过程噪声的协方差表示了目标的机动性，但通常是先验假设的，所以无法准确作为表征目标机动性的参数。新息表示了量测值与预测值之间的差值，新息的大小与过程噪声的协方差和雷达量测噪声的协方差有关，而量测噪声的协方差是雷达的量测精度，为已知量，所以新息可以用作表征目标机动性的参数。由于无法准确地决策来源于目标的真实量测值，因此选择组合新息表征目标机动性的参数。对于单目标跟踪的PDA算法，假设候选回波中只有一个是来自于目标的真实量测值，其余都是虚假量测值，所以对其进行归一化可以得到表征杂波密度的参数：

(11)

式中，V(k)为当前波门的体积。

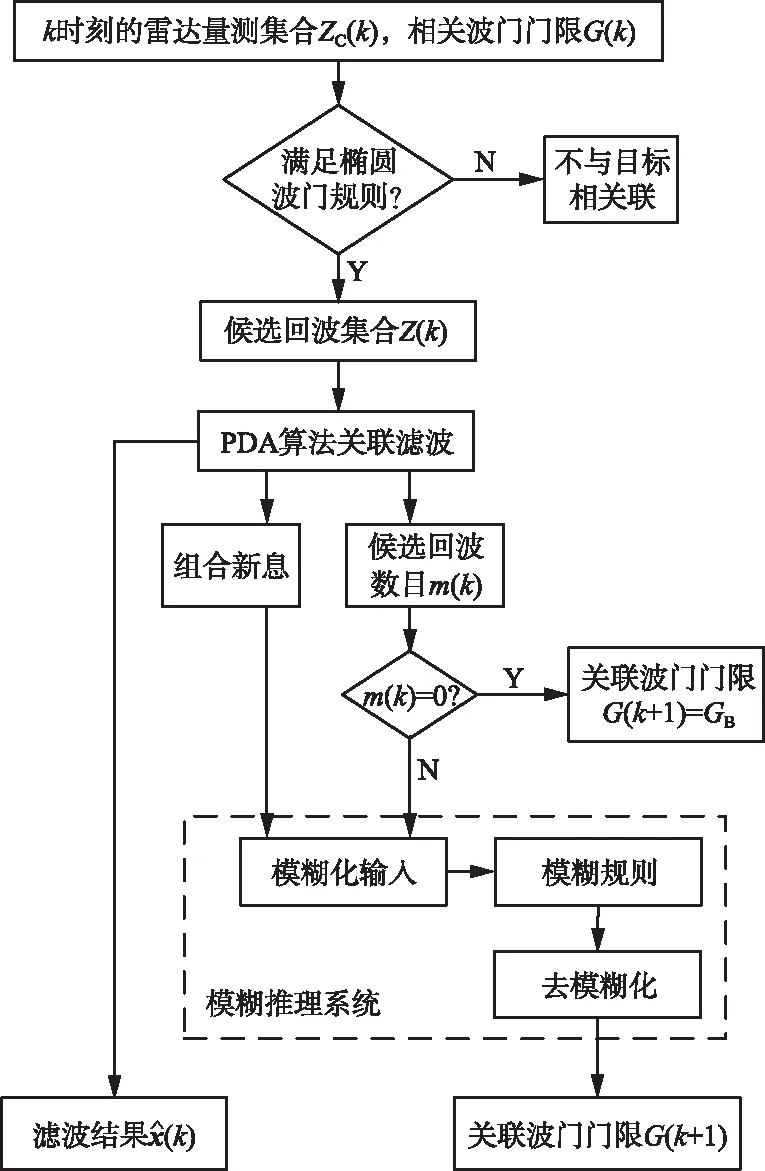
图4 基于模糊推理的自适应关联波门算法流程Fig.4 The flow of adaptive association gate algorithm based on fuzzy inference

定义模糊系统的输入，即组合新息v(k)和归一化候选回波数目m(k)的模糊子集为{S(小)，M(中)，B(大)}，在这里输入的隶属度函数使用高斯型函数，如图5所示。

图5 输入隶属度函数Fig.5 Input membership degree function

其表达式为：

(12)

可以根据雷达的量测精度选择不同的c，σ值，确定输入模糊集合的位置。模糊系统输出为关联波门门限Gout，定义其模糊集合为{VS(较小)，S(小)，M(中)，B(大)}，输出隶属度函数采用高斯型，如图6所示。

图6 输出隶属度函数Fig.6 Output membership degree function

当关联波门内没有候选回波时，即m(k)=0，说明此时目标的机动性特别强，已无法通过模糊推理来调整关联波门门限，所以下一时刻的关联波门门限取最大模糊子集的门限值GB。

步骤2：用模糊规则表征模糊推理过程

由最优关联波门的表达式可知，输出量关联波门门限和输入量存在以下相互约束关系：如果当前的组合新息较小，归一化候选回波数目较小，说明此时目标的机动性小且杂波密度较小，输出量关联波门门限可以取小；而当组合新息较大，归一化候选回波数目较小时，说明目标的机动性略强，那么输出量关联波门门限应当相应的增大。同理，运用Mamdani方法[20]可以把上述模糊推理过程转换为模糊规则表，如表1所示。模糊推理过程的运算为：

表1 模糊规则表Tab.1 Fuzzy rule table

Ri：μ(G)=μ(v)∧μ(N)，

(13)

式中，∧表示取小的符号；μ(v)，μ(N)分别表示在第i个模糊规则中输入对应的模糊子集隶属度函数值；μ(G)表示输出对应的模糊隶属度函数值。

步骤3：去模糊化

采用面积重心法进行去模糊化[21]，对模糊系统输出进行去模糊化，也就是计算输出隶属度函数曲线与横坐标轴围成的面积，输出量为此面积的重心。假设模糊输出集合中的某一元素为Gi，且此处的隶属度为μ(Gi)，则有：

(14)

式中，Gout为关联波门的门限，也就是模糊推理系统输出的精确值。

4 仿真试验与结果分析

为验证基于模糊推理的自适应关联波门方法的性能，选用相同的目标跟踪场景，分别运用自适应关联波门方法与门限不同的固定椭圆波门对单个机动目标进行跟踪，通过仿真实验验证算法的性能。

目标运动场景如下：跟踪对象为杂波环境下二维平面中的单个机动目标，目标起始位置状态为x(0)=[0 m，10 m/s，10 m/s2，0 m，100 m/s，0 m/s2]，目标的运动轨迹如图7所示。杂波的数目服从参数λ的泊松分布且是时变的，杂波位置在以目标预测值为中心的矩形区域内服从均匀分布。

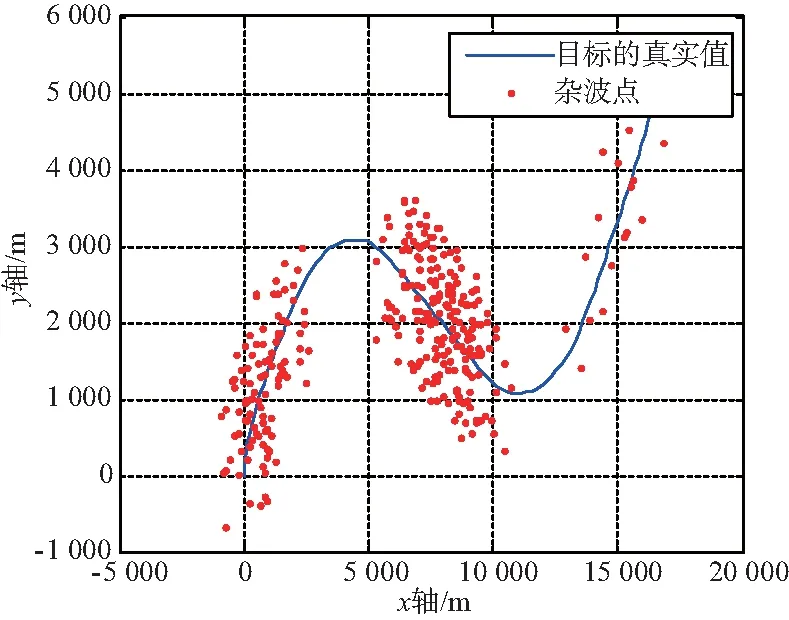
图7 二维平面中单个机动目标的运动轨迹Fig.7 Motion trajectory of single maneuvering target in two-dimensional plane

状态模型及算法：数据关联算法运用PDA算法，其中滤波算法采用匀加速模型的卡尔曼滤波算法。

传感器量测及其他参数：雷达的量测噪声均值为0，方差为100 m2的高斯白噪声，目标的检测概率PD=1，采用椭圆跟踪波门规则，采样间隔T=1 s，每次仿真步数100步。仿真结果由100次蒙特卡罗实验统计得到。

如果连续4个采样周期目标的位置估计误差超过了量测标准差的5倍，则认为丢失目标。定义失跟率为蒙特卡罗仿真中出现丢失跟踪目标的次数占总仿真次数的比例[17]。算法耗时是指不同算法在仿真实验中完成对目标的跟踪所需时间。

在不同关联波门下目标的滤波曲线如图8所示。不同关联波门在目标失跟率和算法耗时方面的性能对比如表2所示。由于丢失目标后的滤波会发散，误差无限增大，会对均方根误差有误导影响，所以统计目标的均方根误差时，剔除了丢失目标的跟踪结果。

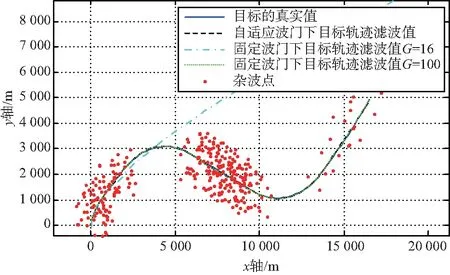
图8 目标轨迹的滤波曲线Fig.8 Filter curve of target trajectory

表2 不同算法性能对比Tab.2 Performance of different algorithms

由图8中可以看出，对于门限较小的固定椭圆波门，在目标发生机动时，很容易丢失目标，跟踪性能最差，而自适应波门与门限较大的固定椭圆波门能够较好地跟踪目标。由于门限较小的固定椭圆波门丢失了目标，其滤波结果中的目标位置均方根误差越来越大，所以在图9中没有画出其曲线。

目标位置的均方根误差曲线和目标速度的均方根误差曲线如图9所示。

图9 目标跟踪状态的均方根误差曲线Fig.9 Root mean square error curve of target tracking state

由图9可以看出，门限较大的固定椭圆波门的均方根误差要大于自适应波门，所以自适应波门提高了对目标的跟踪精度。

由表2可以看出，门限较小的固定椭圆波门的失跟率最高，这是显而易见的，自适应波门的失跟率比门限较大的固定椭圆波门降低了21%，算法耗时增加了13.3%。对于算法的耗时对比，由于固定波门存在丢失目标的情况，所以不需要进行滤波处理，这将会导致算法耗时大大降低，从理论上分析，自适应波门方法能够减少波门内候选回波数目，是可以降低计算量的。

5 结束语

在PDA算法框架下，提出了一种基于模糊推理的自适应关联波门的设计方法，该方法主要借鉴模糊推理的思想求解最优波门数学模型，首先根据雷达的量测信息和滤波结果，提取出表征目标机动性和杂波密度的参数，然后通过查询模糊规则表，推理出关联波门的门限值。其中自适应关联波门的设计，可以得到近似最优的量测点迹集合，进一步降低目标失跟率，提高了跟踪精度。通过仿真实验对比测试，验证了自适应关联波门的设计方法在轻微增加算法耗时的情况下能够有效提高杂波环境下的机动目标跟踪能力。另外，本文提出的自适应波门方法只考虑了单目标场景下的跟踪问题，针对杂波中多目标的跟踪问题将是下一步需要研究的内容。