基于窗函数频谱设计NLFM信号波形的方法性能分析

马 兰 张苡宁 李照照 井 伟 陈俩兴

(1.西安电子工程研究所 西安 710100；2.中国人民解放军32382部队 北京 100071)

0 引言

由于NLFM信号脉压时无需作加权处理便可获得较低的副瓣，近年来广泛受到关注。相较于LFM信号，NLFM信号的改进主要是将经过匹配滤波后的信号主副瓣比提高，同时减小脉压时的SNR损失。本文是基于相位逗留原理，首先通过利用窗函数的频谱来求出群时延函数，对群时延函数作插值拟合将频率函数估计出来，再根据NLFM信号相位函数与频率函数的关系，可对频率函数累加求和计算出相位函数，最后得到NLFM信号波形。

文献[1]主要是根据脉压输出波形峰值主副瓣比或主瓣宽度的实际需求来设计NLFM信号，采用的方法是动态优选法，该方法运算量小，灵活性高，但设计的前提是已知脉压结果的主副瓣比或主瓣宽度[1]。文献[2]是从NLFM信号的最小峰值旁瓣抑制器出发，采用凸优化方法进行实现并设计了一种新的NLFM信号，通过迭代法进一步抑制了信号的距离旁瓣。该方法主要适用于小时宽带宽积的NLFM信号的设计[2]。文献[3]是通过设计振幅窗函数并对NLFM信号进行脉压处理来获得较低的副瓣电平，该方法的缺点是幅度加权会带来一定的SNR损失[3]。

为更好地满足实际需求，本文对所设计的NLFM信号进行了谱修正滤波处理[4-5]，在主瓣展宽和主副瓣比可接受的范围内，进一步降低了信号的旁瓣电平，改善了NLFM信号的脉压性能。同时，对NLFM信号的多普勒容限进行了验证，实验结果表明，NLFM信号对多普勒频移敏感[6-8]。

1 基于窗函数频谱设计NLFM信号的基本原理

假设NLFM信号的频谱为

(1)

由于匹配滤波器的传输函数h(t)与输入信号s(t)之间满足关系式(2)为

h(t)=ks*(t0-t)

(2)

其中，k为一常数，一般令其为1，t0表示回波信号的时延，一般都假设为0，因此，式(2)可以简写为

h(t)=s*(-t)

(3)

则匹配滤波器的频域表达式为

H(f)=S*(f)

(4)

故信号经过频域脉压之后的频域输出为

Y(f)=S(f)·H(f)=S(f)·S*(f)=|S(f)|2

(5)

根据相位逗留原理，脉压输出Y(f)会与一个理想的窗函数W(f)等价，即

Y(f)=|S(f)|2=W(f)

(6)

其中，W(f)为理想窗函数的频域表达式。

根据信号相位函数θ(f)与信号频谱S(f)的关系

(7)

以及群时延函数的频域表达式T(f)与相位函数的一阶导数θ′(f)的关系为

(8)

可知，群时延函数具有如表达式(9)所示。

(9)

其中，B为信号带宽，Ka为常数，其表达式为

(10)

其中，T为信号脉冲宽度。

由于频率函数f(t)是群时延函数T(f)的反函数，即

f(t)=T-1(f) (-T/2≤t≤T/2)

(11)

由于常见的窗函数频谱表达式W(f)均是由一些正余弦项组成，故对其进行积分得到的群时延函数表达式T(f)也必定是一些与正余弦相关的项，求其反函数一般较为困难。通常，频率函数f(t)的求取是对群时延函数T(f)进行插值拟合来近似获得。具体如下：

假设dt为采样间隔，df为均分带宽，tf为群时延函数元素值，则频率函数f(t)的元素组成近似可以表示为

(12)

最后，根据相位函数φ(t)与频率函数f(t)的关系

(13)

对频率函数累加求和得到相位函数各元素值。

假设NLFM信号的表达式为

y(t)=a(t)ejφ(t)

(14)

令幅度函数a(t)=1，并将相位函数φ(t)代入，就可得到NLFM信号表达式。

2 NLFM信号的低旁瓣脉冲压缩

2.1 NLFM信号的脉压性能仿真分析

假设在NLFM信号的设计过程中分别选择Hanning窗、Hamming窗和Blackman窗的频谱进行设计，则它们的频域表达式分别为

W1(f)=0.54-0.46cos(2πf/B)

(15)

W2(f)=0.42-0.5cos(2πf/B)+0.08cos(4πf/B)

(16)

W3(f)=0.5-0.5cos(2πf/B)

(17)

结合式(9)和式(10)分别得到对应的群时延函数为

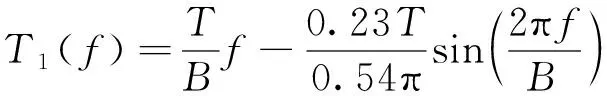
(18)

(19)

(20)

根据式(12)的插值拟合方法，可以得到频率函数对应的近似S型曲线。

假设雷达仿真参数设计如表1所示。

表1 仿真参数设计1

具体设计过程如下：

1)Hanning窗函数下的仿真分析：

图1 Hanning窗频谱波形

图2 群时延函数曲线

图3 近似频率函数曲线

图4 相位函数曲线

图5 NLFM信号波形

图6 NLFM信号频谱特性

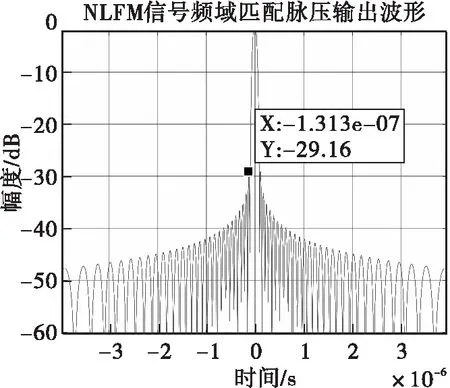
图7 NLFM信号频域匹配脉压波形

2)Hamming窗函数下的仿真分析：

图8 Hamming窗频谱波形

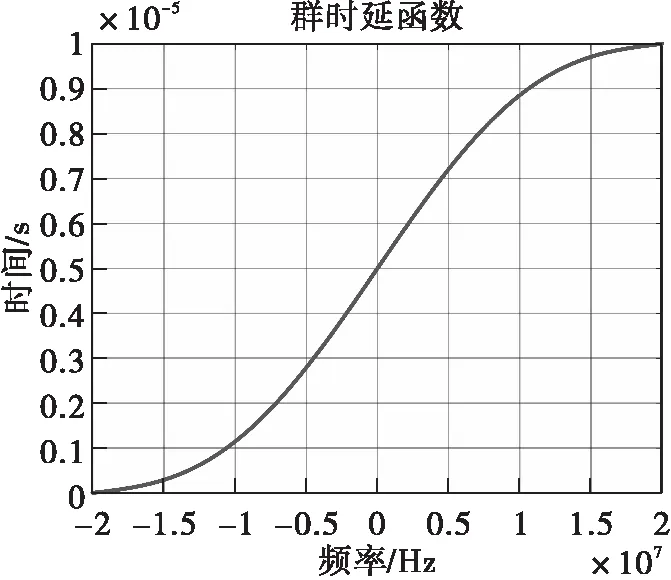
图9 群时延函数曲线

图10 近似频率函数曲线

图11 相位函数曲线

图12 NLFM信号波形

图13 NLFM信号频谱特性

图14 NLFM信号频域匹配脉压波形

3)Blackman窗函数下的仿真分析：

图15 Blackman窗频谱波形

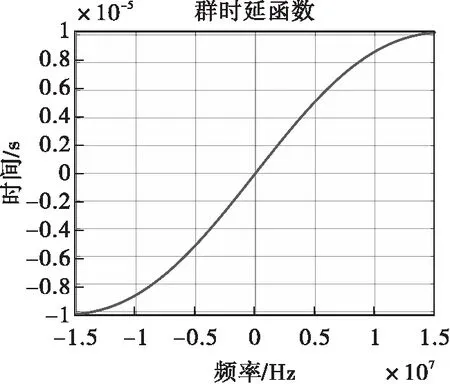
图16 群时延函数曲线

图17 近似频率函数曲线

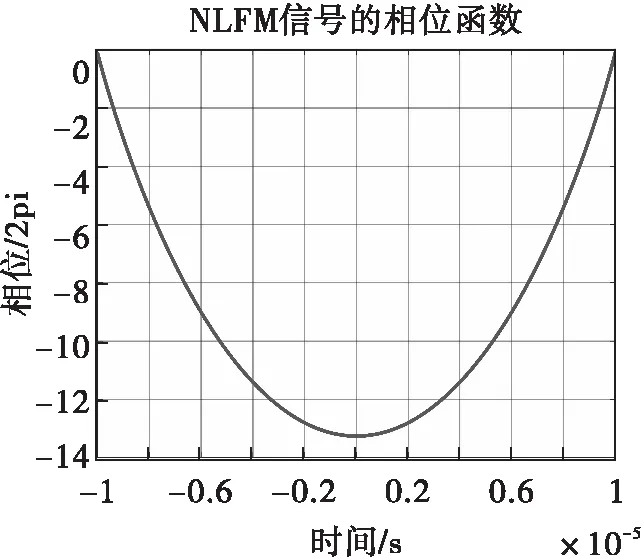
图18 相位函数曲线

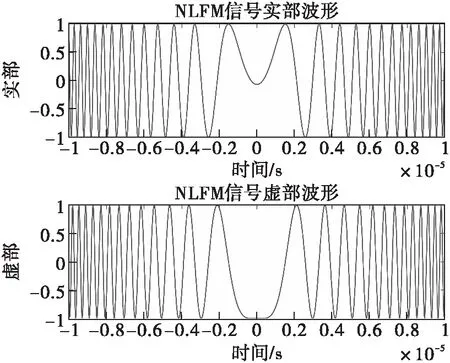
图19 NLFM信号波形

图20 NLFM信号频谱特性

图21 NLFM信号频域匹配脉压波形

比较三种窗函数下的仿真结果可以看出，在该组雷达设计参数下，利用Hamming窗设计的NLFM信号具有较好的脉压性能，其频域匹配脉压波形主副瓣比仅为-36.19dB。相比于LFM信号，NLFM信号具有较好的低旁瓣电平脉压性能。

2.2 谱修正后NLFM信号的脉压性能仿真分析

由于在NLFM信号波形的设计过程中，求取频率函数采用了插值拟合的方法，因此最终得到的信号波形与理论结果存在一定的偏差。为进一步降低NLFM信号的旁瓣电平，使其信号频谱更接近于理想窗函数，考虑到直接加权会引起SNR损失，有人提出了采用谱修正滤波器[9-10]来改善NLFM信号脉压性能。

谱修正滤波原理如图22所示，其中，s(n)表示NLFM信号的离散形式；h′(n)表示谱修正滤波器的离散形式；w(n)表示理想窗函数的离散形式。

图22 谱修正滤波原理框图

假设谱修正滤波后的信号输出为理想窗函数，则可以得到谱修正滤波器的频域表达式为

(21)

其中，W(f)为理想窗函数频域表达式；S(f)为设计的NLFM信号频域表达式。

假设雷达仿真参数设计如表2所示。

表2 仿真参数设计2

仿真结果如图23至图26所示。

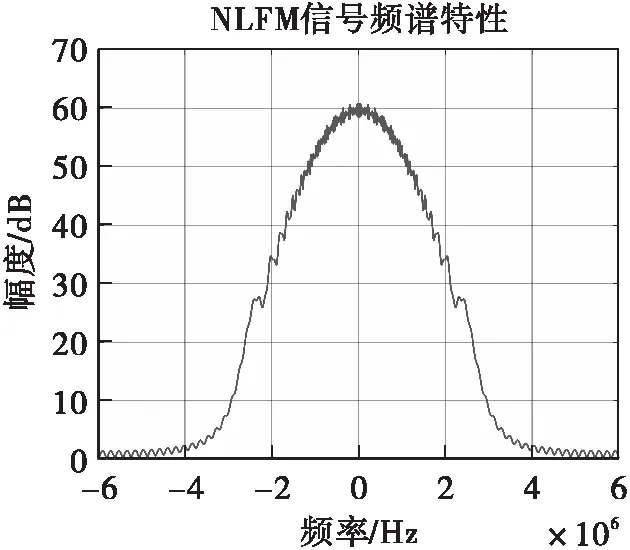
图23 NLFM信号频谱特性

图24 谱修正后NLFM信号频谱特性

图25 NLFM信号匹配脉压结果

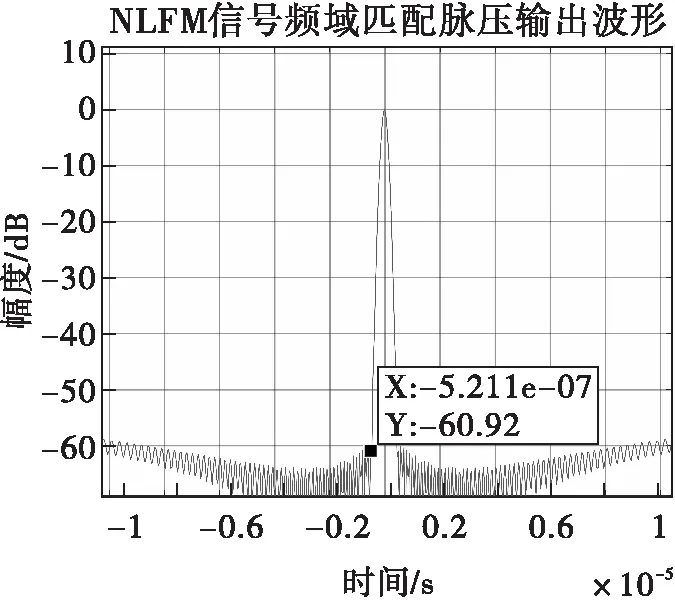
图26 NLFM信号谱修正滤波脉压结果

对比图25和图26可以看出，相较于直接对NLFM信号作匹配脉压，经过谱修正滤波后NLFM信号的副瓣电平明显降低，大约为16dB左右，故谱修正滤波可以明显改善NLFM信号的脉压性能。

由于实际脉压结果受很多因素的影响，下面针对信号时带积和采样率对脉压结果的影响进行对比分析。

如表3所示，分别选择时带积为480和600，采样率为fs=2B和fs=4B，且每种情况下分别选择Hamming、Blackman和Hanning窗函数进行谱修正滤波处理，仿真结果如表4所示。

表3 仿真参数设计3

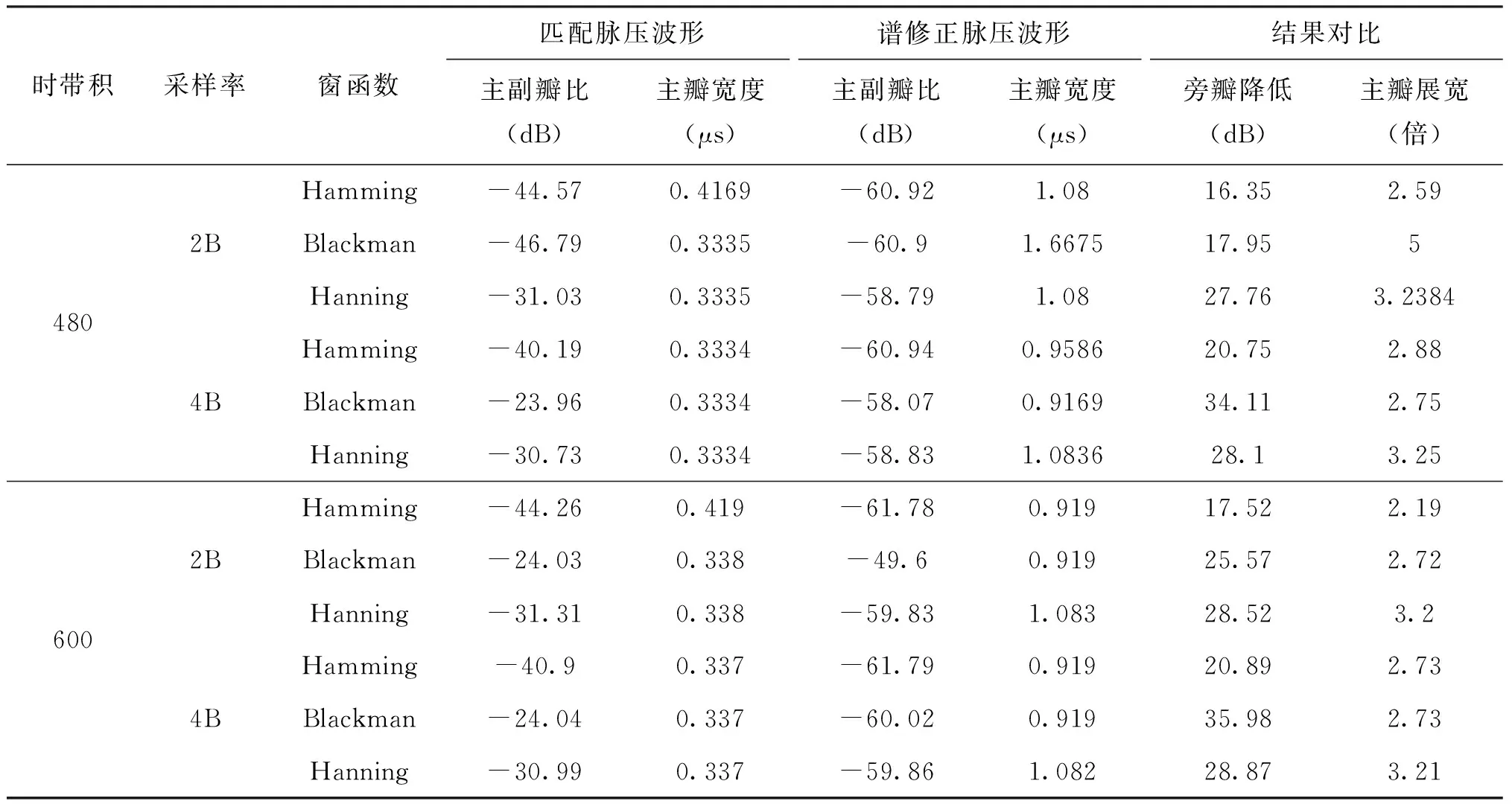
表4 不同因素对NLFM信号脉压性能的影响对比分析

从表4可以看出，随着时带积的增加，NLFM信号的脉压性能越来越好；随着采样率的增加，谱修正滤波之后NLFM信号的旁瓣电平被进一步抑制，且当fs=2B时，选取的三种窗函数中Hanning窗的旁瓣抑制性能最好；当fs=4B时，Blackman窗的旁瓣抑制性能最好；谱修正滤波器的引入可以改善NLFM信号的脉压性能，但同时也带来了一定的主瓣展宽。

综合考虑，在脉压波形主瓣展宽可接受范围内，通过谱修正滤波降低NLFM信号的副瓣电平是可行的。

3 NLFM信号的多普勒容限

假设仿真参数设计如表1所示，多普勒频率fd分别取±10kHz、±50kHz，则加入fd后NLFM信号的匹配脉压结果如图27所示。

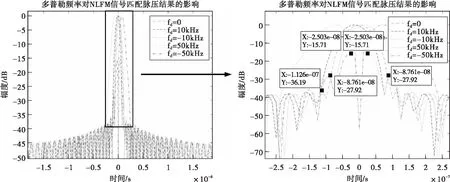
图27 多普勒频率对NLFM信号匹配脉压结果的影响

根据仿真结果可以看出，当多普勒频率fd=±10kHz时，NLFM信号匹配脉压波形的主副瓣比由-36.19dB增加至-27.92dB；当多普勒频率fd=±50kHz时，输出波形主副瓣比增加至-15.71dB。故当回波信号中有较大的多普勒频移时，匹配滤波器将不能起到较好的脉冲压缩作用，即NLFM信号是一种多普勒敏感信号。

4 结束语

本文基于相位逗留原理，利用不同窗函数频谱对NLFM信号波形进行了设计，比较了不同窗函数频谱下设计的NLFM信号脉压性能。实验结果表明，Hamming窗具有更好的脉压性能，且相较于LFM信号，NLFM信号匹配脉压结果具有较好的低旁瓣电平。同时，仿真分析了多普勒频移对NLFM信号匹配脉压波形的影响，仿真结果验证了NLFM信号是一种多普勒敏感信号。