五次多项式优化的平行泊车路径规划

胡勤明，王金刚，张小俊

河北工业大学 机械工程学院，天津 300132

近几年，我国的汽车保有量快速增长，但城市的停车位已无法适应汽车数量的快速增长，拥挤的停车场给驾驶员泊车入位带来了很大的难度。因此，人们对于自动泊车系统的需求越来越强烈。目前，自动泊车技术主要分为三个方面：环境感知、路径规划和跟踪控制。本文将主要从自动泊车路径规划的角度进行研究。

Sungwoo等[1]、张持等[2]采用两段相切圆弧的方式规划平行泊车的路径；Zhdanov等[3]采用圆弧与直线相结合的方式规划平行泊车路径，上述两种泊车路径规划的方简单、计算效率高，但在切点处存在路径曲率突变。Qin等[4]利用圆弧-直线进行泊车路径初次规划并使用贝塞尔曲线对初始路径进行平滑处理。Vorobieva等[5]、张家旭等[6-7]采用回旋曲线对泊车路径进行平滑处理，避免车辆出现前轮原地转向的情况，并提出了车辆在狭小车位泊车的路径规划方法。李红等[8]、吴中伟[9]基于车辆运动学模型对泊车碰撞进行了分析，并建立约束方程避免碰撞，然后通过B样条曲线进行自动泊车路径规划，所得路径曲线的曲率连续无突变。胡文等[10]提出了基于驾驶员经验的自动泊车规划算法，按驾驶员的操作习惯将泊车路径分为六段，根据控制需求对每段路径进行不同的求解计算，解决原地转向问题。Zhang等[11]、黄江等[12]基于五次多项式对泊车路径进行优化，整条路径均为多项式曲线，保证了路径曲率的连续性。五次多项式路径曲线不仅光滑、具有连续的曲率，还能保证加加速度（Jerk）连续变化。Takahashi等[13]已经证明：任何Jerk最优化问题中的解都可以使用一个五次多项式来表示。Jerk直接关系到车内人员的舒适度，Jerk连续平缓的变化可以确保乘客拥有舒适的乘车体验。上述方法虽然对泊车路径进行了优化，不过还存在一些不足：如B样条曲线求解复杂、计算量偏大；整条路径均为五次多项式曲线的平行泊车路径需要的泊车位尺寸较大；回旋曲线无法使Jerk连续平缓变化等。

借鉴以上研究的优势与不足，提出一种五次多项式优化的平行泊车路径规划方法。考虑到多项式如果低于五次则无法获得具有较优Jerk的曲线，如果高于五次则会导致计算量偏大，因此选用五次多项式。在自动泊车的过程中，整条路径均为五次多项式曲线的路径需要的泊车位尺寸较大，车辆只有保持以较小的转弯半径不变进行转向，所需的最小平行泊车位尺寸才能较小，所以在“圆弧-直线-圆弧”路径的基础上，只对曲率突变处进行平滑过渡，而其他部分仍为直线或圆弧。

1 车辆运动学模型

车辆运动学模型在阿克曼转向几何的基础上建立，且将车辆视为刚体。车辆在泊车的过程中，车速一般小于10 km/h，无需考虑车轮的滑移，认为车轮只做滚动和转向运动；如图1所示，为简化泊车路径规划时的避障分析，通常将车辆外形简化成矩形，矩形的大小为车身的最大外形尺寸。

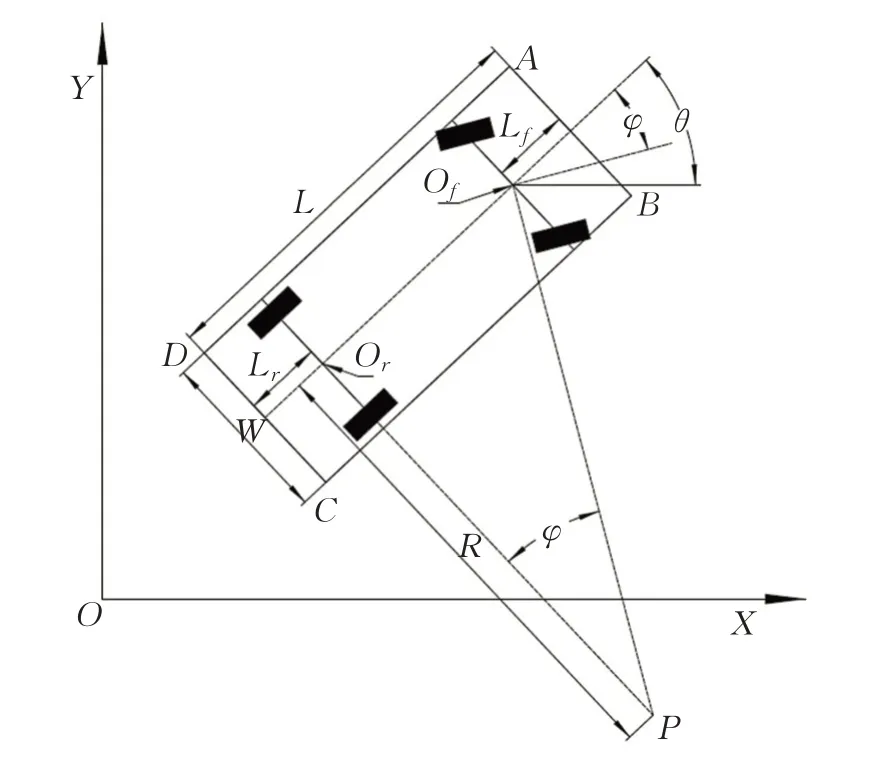
图1 车辆运动学模型Fig.1 Vehicle kinematics model

由于车辆后轮的运动方向始终与车身的运动方向相同，因此车辆的位置坐标选在车辆后轴中心点(xr,yr)。车辆参数符号如表1所示。

建立车辆的运动学模型：

式中，xr和yr分别为车辆后轴中心点处的横、纵坐标；θ为车身航向角；vr为车辆后轴中心点处的速度；ω为车身转动角速度。

为方便描述车辆在某一点处的位置和航向角，定义车辆的位姿状态为Sn=(Xn,Yn,θn)。

表1 车辆参数符号Table 1 Symbols for vehicle parameters

2 多项式过渡曲线

在自动泊车的过程中，若车辆的泊车路径存在曲率突变点，当车辆匀速经过该位置时，理论上需要转向盘在瞬时由当前角度转到另一个角度，但这是不可能实现的，所以路径的曲率突变点最终会导致车辆的实际行驶路径与规划路径相比产生较大偏差。

“多项式过渡曲线”的核心是以多项式曲线作为过渡曲线，来保证路径曲率平滑过渡。如图2所示，设过渡曲线的起点O为坐标系原点，则车辆的初始状态为S0=(X0,Y0,θ0)=(0,0,0)。如果车辆直接以最小转弯半径Rmin向左转动，则车辆的转动瞬心为C01=(0,Rmin)。圆C00由圆C01平移得到，其圆心坐标为(XC00,YC00)=(Lccosμ,Lcsinμ+Rmin)。“多项式过渡曲线”的终点P在圆C00的某一位置，选取合适大小的角λ，并定义为过渡角，过渡角便决定了点P的坐标。另外，设偏角为ψ，直线OC00的长度为R0。其中R0可以由余弦定理计算得出：

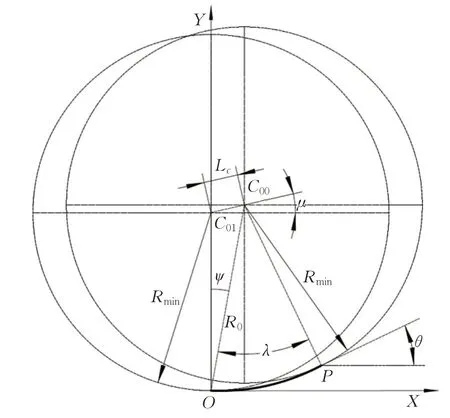
图2 多项式过渡曲线Fig.2 Polynomial transition curve

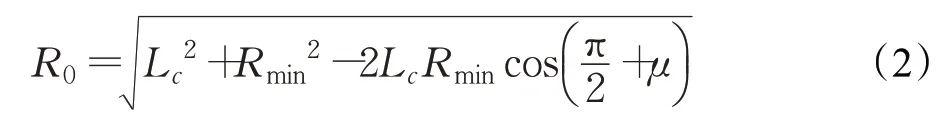
偏角ψ可由正弦定理计算得出：

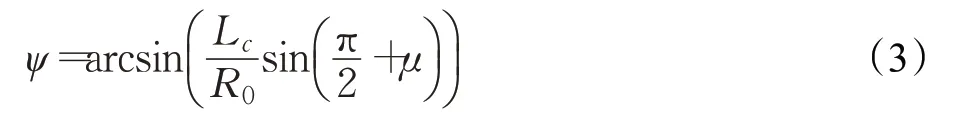
进而可计算出过渡曲线终点P的坐标：

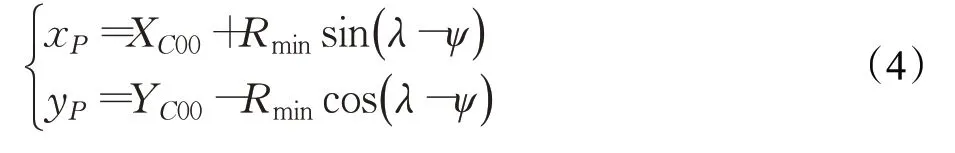
过渡曲线终点P处的切线与X轴之间的夹角为：

则车辆在过渡曲线终点P处的位姿状态为SP=(xP,yP,θP)。

设过渡曲线的表达式为：

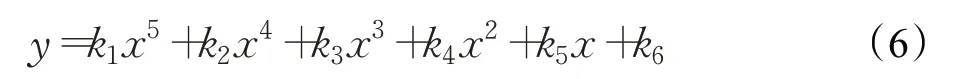
式中，k1～k6为过渡曲线表达式的系数[14]。

设车辆在过渡曲线起点和终点的坐标分别为(xO,yO)和(xP,yP)，由此可得：

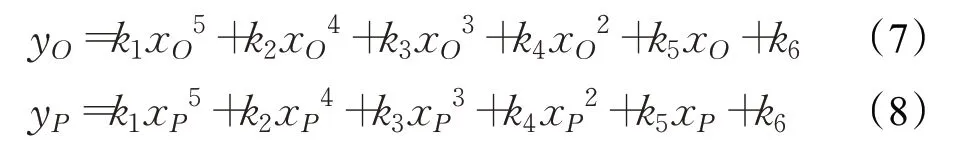
将过渡曲线的表达式（6）对x求导可得：

因为车辆在过渡曲线的起点和终点处的航向角分别为θO和θP，所以可以得到如下约束方程：

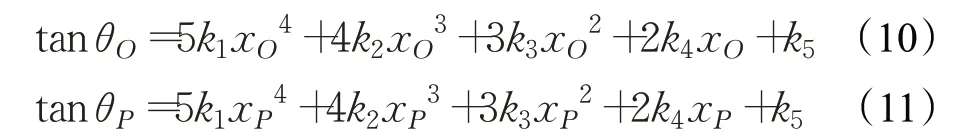
过渡曲线还需要保证曲率的连续性，其中曲率的计算公式为：

根据曲率计算公式（12）可计算出过渡曲线的曲率方程为：

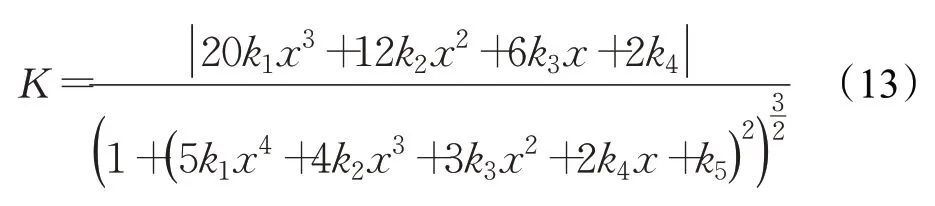
因为过渡曲线为五次多项式，过渡曲线的曲率必定连续，但过渡曲线的起点和终点在与其他曲线相切时，曲率也不能存在跳变。图2中O点可以认为是过渡曲线与水平线相切，P点可以认为是过渡曲线与半径为Rmin的圆弧相切，两点处的曲率应分别为KO=0和KP=1/Rmin，因此可得出以下约束方程：

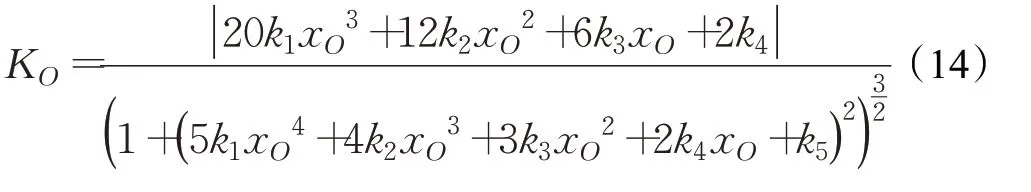
将式（7）、（8）、（10）、（11）、（14）和式（15）联立便可节出系数k1～k6，从而可以得到车辆的过渡曲线。

得出过渡曲线后，车辆可沿过渡曲线切入到半径为Rmin的圆C00路径上，当车辆沿圆C00路径再转过一定角度后，车辆的转向盘还需要回正，这一个过程同样可以用上文提出的“多项式过渡曲线”。

如图3所示，为简化后续路径规划的复杂度，以C00为圆心，RO为半径作圆，此圆弧称为虚圆路径，其起点和终点分别为O点和N点。

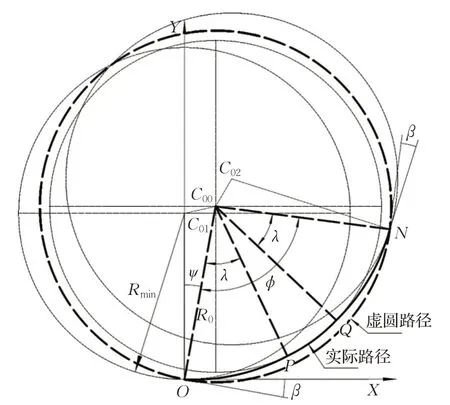
图3 虚圆路径Fig.3 Virtual circle path

其中，在虚圆路径的起点O和终点N处，车身航向与虚圆路径切线的夹角为β，其中β=ψ。因此，引入虚圆路径后，只需要知道车辆的初始状态S0、圆心C00的坐标、虚圆半径R0和虚圆路径转过的角度φ，就可以快速地由几何关系计算出车辆的转弯末状态SN，进而根据上文确定的过渡角λ求出P点和Q点处的车辆位姿状态SP和SQ，最终便可由上文的方法解出过渡曲线OP、QN和圆弧曲线PQ。虚圆路径的引入为实际转弯路径以及后续的路径规划提供了便捷，大大提高了计算效率。

如图4所示的路径称为“圆弧-直线-圆弧”平行泊车路径，以下简称“C-L-C”路径。由于O1O2和O3O4段的转弯半径固定不变，所以路径曲率在起点、终点以及圆弧与直线的相切点上均存在突变。本文基于上述“多项式过渡曲线”对“C-L-C”路径进行优化。因为车辆在低速运动的情况下车轮不会产生横向和纵向滑移，所以规划平行泊车路径时可使用“逆向工程”的方法，即规划出一条车辆从平行泊车位驶出的路径。

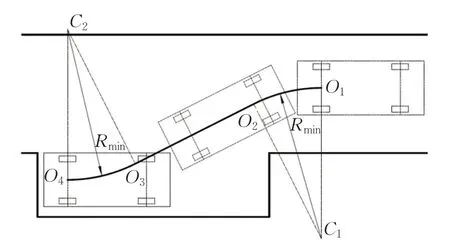
图4“圆弧-直线-圆弧”路径Fig.4“C-L-C”path

3 最小平行泊车位尺寸计算

3.1 最小平行泊车位长度分析

如图5所示，设平行泊车位的4个顶点分别为a、b、c、d，其中d点设为坐标系的原点。为降低碰撞风险，在车辆四周取长度为Lsafe的安全距离。所以在终点O4处S4=(X4,Y4,θ4)=(Lsafe+Lr,W/2,0)。

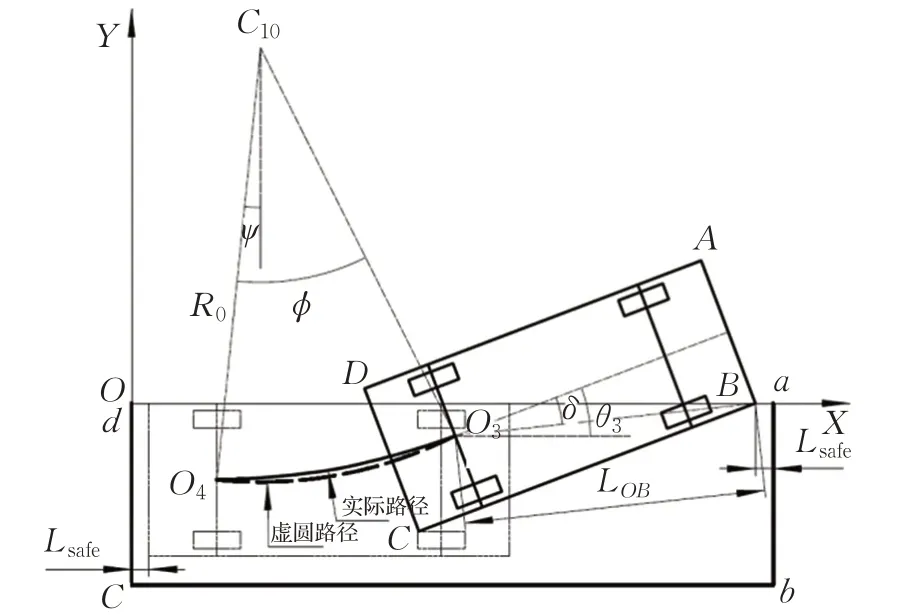
图5 最小平行泊车位长度分析Fig.5 Analysis of minimum parallel parking space length

按“逆向工程”的方法，车辆左转向驶出平行泊车位，当车身的B点与车位的a、d点在同一条直线上时，车辆的转向盘完成回正，车辆将沿直线前进继续驶离平行泊车位。在该位置时，车身的B点与平行泊车位的a点的最小距离为Lsafe[12]。若求出B点的坐标(XB,YB)，则平行泊车位的最小长度为：

设虚圆路径转过的角度为φ，则O3处车辆的横、纵坐标及车身航向角分别为：

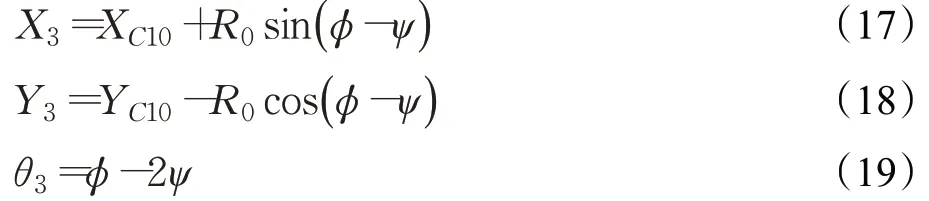
根据车辆在O3点处的坐标及车身航向角可得出车身B点的坐标：

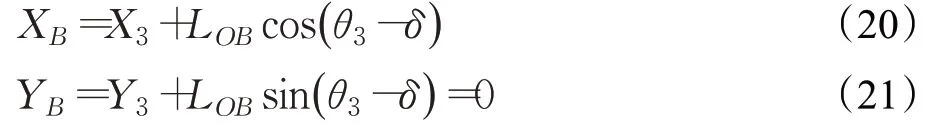
将式（16）～（21）联立便可解出平行泊车位的最小长度LPmin以及车辆在O3点处的位姿S3=(X3,Y3,θ3)。

3.2 最小平行泊车位宽度分析

平行泊车位的最小宽度取决于车身C点的运动轨迹，即C点轨迹纵坐标的最小值YCmin。车辆从O4点驶出泊车位时，车辆会首先沿过渡曲线行驶，过渡曲线的曲率半径是由∞逐渐过渡到Rmin，由几何关系易知曲率半径越小，则YCmin的数值越小。所以，如图6所示，为了简化计算，将车辆直接以最小转弯半径Rmin驶出平行泊车位，车身C点沿曲率半径为RC的路径CC′运动，其中曲率半径RC的大小为：

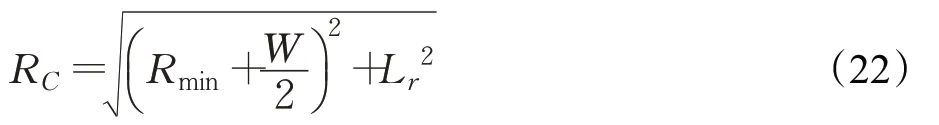
则路径最低点的纵坐标为：

所以，最平行小泊车位的宽度为：

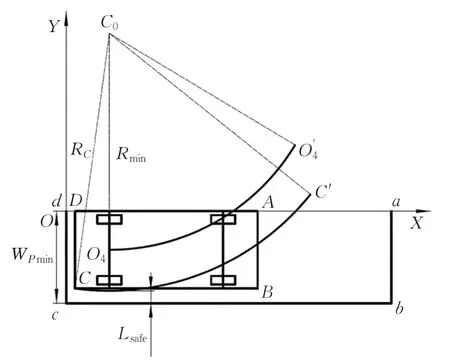
图6 最小平行泊车位宽度分析Fig.6 Analysis of minimum parallel parking space width

4 泊车可行起始区域分析

4.1 道路上边界碰撞分析

如图7所示，车身AD边易与道路上边界mn发生碰撞，因此需要确定泊车起始点O1纵坐标的上极限Y1max，这与分析最小平行泊车位宽度相同，Y1max的大小取决于车身A点轨迹纵坐标的最大值YAmax。同理，为了简化计算，将车辆直接以最小转弯半径Rmin行驶，车身A点沿曲率半径为RA的路径AA′运动，其中曲率半径RA的大小为：

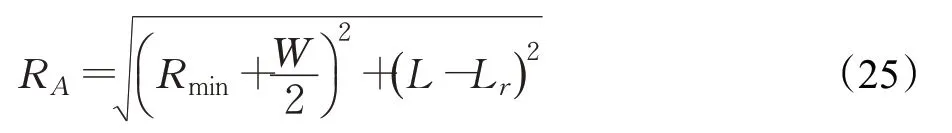
则车身A点运动轨迹最高点的纵坐标为：

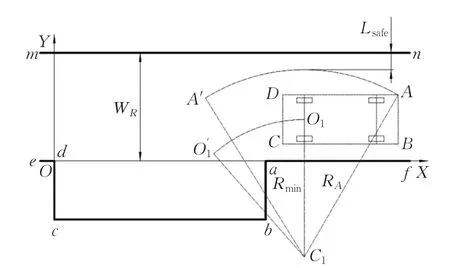
图7 道路上边界碰撞分析Fig.7 Collision analysis of upper road boundary

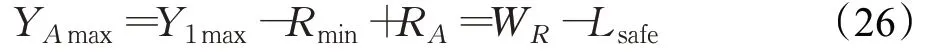
式中，WR为道路的宽度。

将式（25）与式（26）联立可解出车辆泊车起始点O1纵坐标的上极限Y1max。

4.2 道路下边界碰撞分析

如图8所示，避免车身BC边与道路下边界af发生碰撞，关键在于O2的坐标。车辆后轴线与车身BC边的交点记为K，因为K点运动轨迹的曲率半径最小，所以车辆在从O2点向O1点行驶时，只需要考虑避免车身K点与道路下边界的a点发生碰撞。当车辆在O3点时，记此时车身A点的位置为M，车辆沿直线行驶，当车身的K点到达M点位置时，记此时车辆坐标为O2min，即O2点的下极限位置。

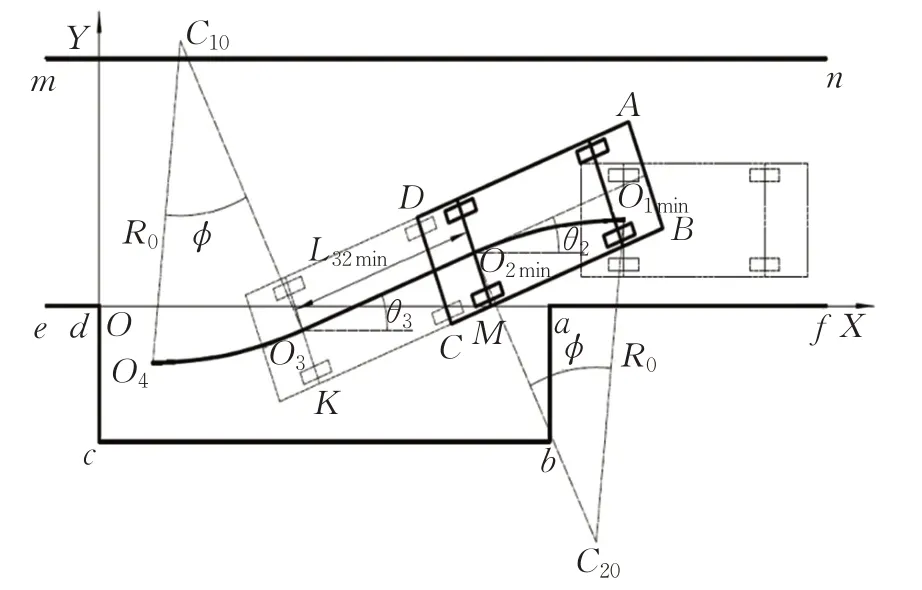
图8 道路下边界碰撞分析Fig.8 Collision analysis of under road boundary

设O2min点与O3点间的距离为L32min，车辆在O2min点处的位姿状态为S2min=(X2min,Y2min,θ2)，其中θ2=θ3，另外：

M点的纵坐标为：

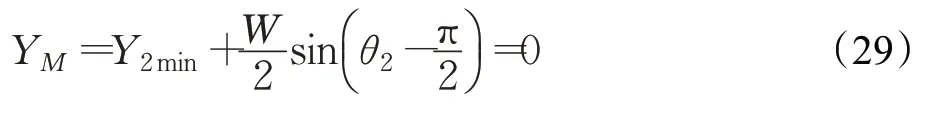
将式（27）、（28）、（29）联立可求解出O2min的坐标。

4.3 确定泊车可行起始区域

泊车可行起始区域是由泊车起始极限位置O1min和O1max决定的。在上文分析车身BC边与道路下边界af的碰撞情况时，已经求解出O2min点的坐标，所以可求出O1下极限O1min点的坐标：

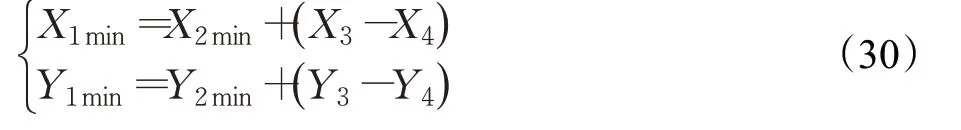
如图9所示，O2O3段直线路径与X轴之间的夹角为θ3，而且由几何关系易知泊车可行起始区域的边界O1maxO2max与X轴之间的夹角也为θ3，所以O1max点的横坐标为：

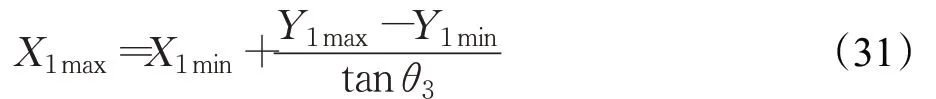
所以，泊车可行起始区域为：

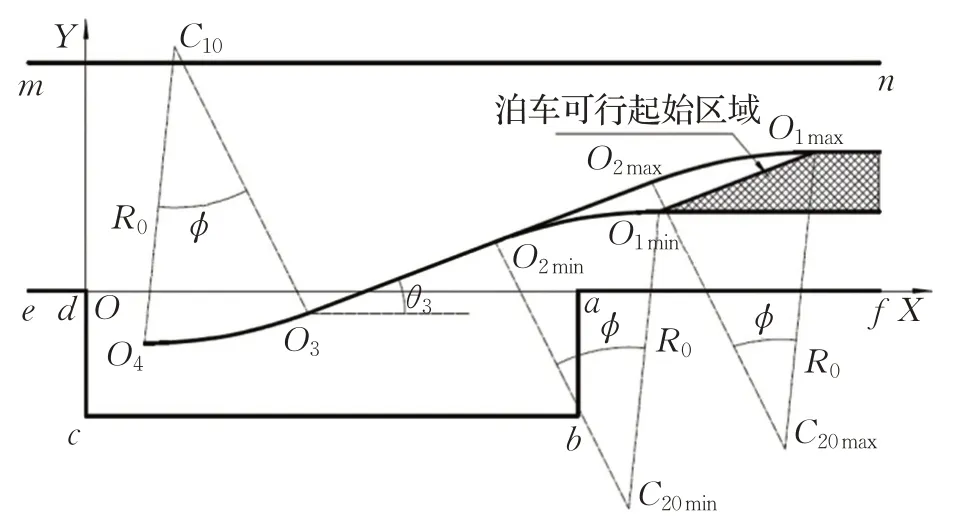
图9 泊车可行起始区域分析Fig.9 Analysis of parking availability starting area

5 仿真验证

5.1 路径规划仿真

基于以上所提出的路径规划算法以及车辆的运动学约束和碰撞约束，建立平行泊车仿真模型。根据某车型的尺寸参数，仿真模型的车辆参数设置如表2所示。

表2 车辆参数Table 2 Vehicle parameters

根据城市道路工程设计规范[15]，平行泊车位的尺寸设置为7 m×2.4 m，道路宽度设置为3.5 m。同时，车辆四周的安全距离设为Lsafe=200 mm。为避免偶然性，选取两个不同坐标点（10，1.5）和（10，1.7）作为泊车的起始点，进行两组平行泊车仿真，两组仿真实验分别记为A组和B组。

如图10所示，A、B两组的优化路径均能够避免边界碰撞、完成平行泊车。由图11（b）和图12（b）中优化路径与C-L-C路径的航向角变化对比可知，A、B两组车辆在倒车泊车的过程中，优化路径的航向角均先发生变化，而且优化路径的最大航向角要小于C-L-C路径的最大航向角，因此在图11（a）和图12（a）中表现为：优化路径所需的X向距离要略长但路径更为平缓。图11（c）和图12（c）为两种路径的曲率随X坐标的变化对比，从图中的两组仿真结果可以看出，C-L-C路径的曲率在整个泊车过程中存在四个曲率突变点，而且完成泊车时路径的曲率未归零，即车辆前轮仍未回正；优化路径的曲率无突变点，曲率的最大值与最小值之间由一段曲线过渡，可避免因路径曲率突变所导致路径跟踪误差。

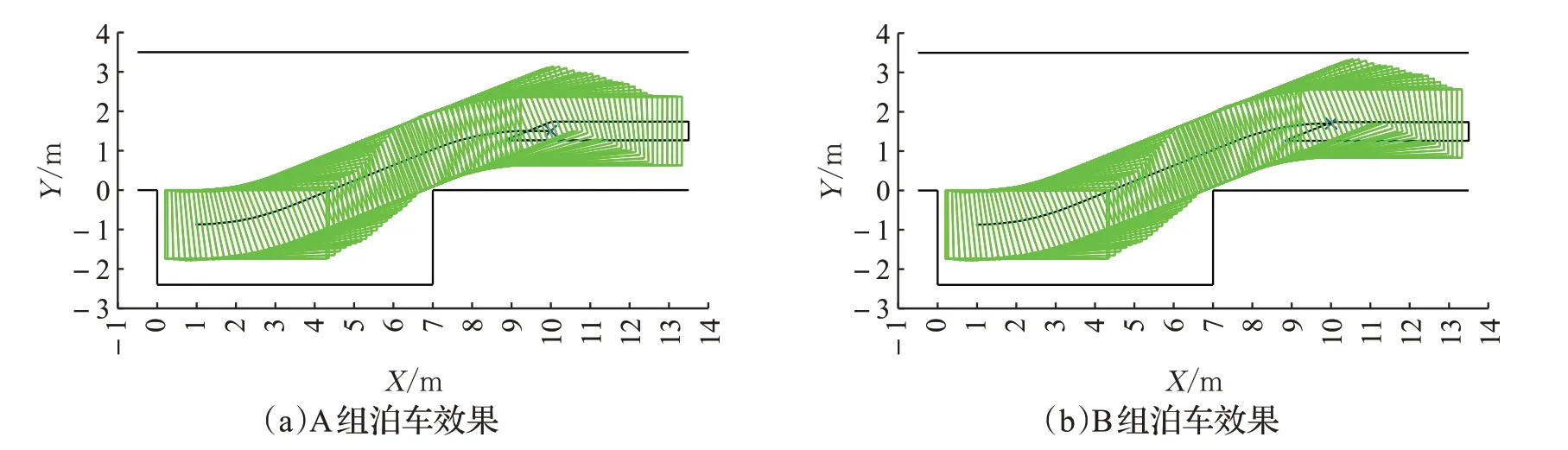
图10 优化路径泊车仿真效果Fig.10 Parking simulation of optimized path

5.2 路径跟踪仿真

为验证优化路径对路径跟踪效果的改善，基于MPC（模型预测控制）[16-18]算法在Simulink中搭建路径跟踪控制模型，车辆的运动速度设为5 km/h，将CarSim与Simulink进行联合仿真，分别对优化路径和C-L-C路径进行路径跟踪，对比两组仿真实验中路径跟踪的效果。

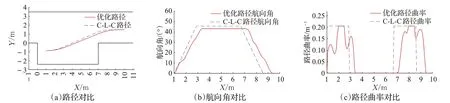
图11 A组起点为（10，1.5）的路径规划仿真结果Fig.11 Path planning simulation results of group A starting point（10，1.5）

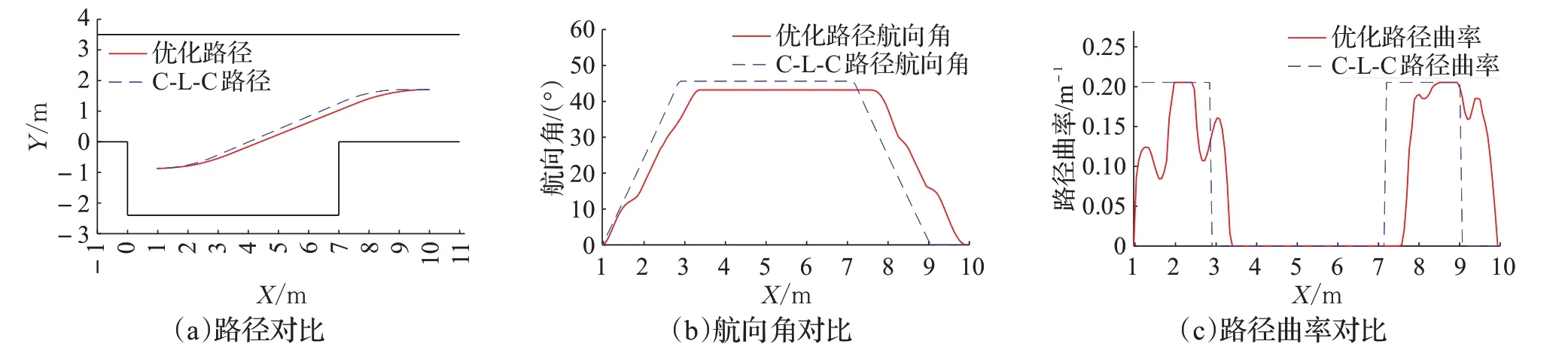
图12 B组起点为（10，1.7）的路径规划仿真结果Fig.12 Path planning simulation results of group B starting point（10，1.7）

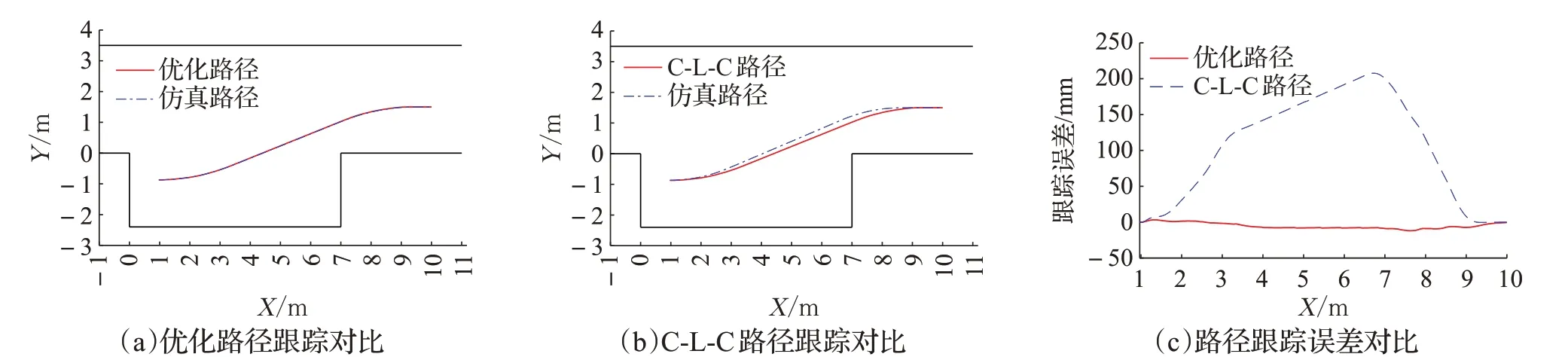
图13 A组起点为（10，1.5）路径跟踪仿真实验Fig.13 Path tracking simulation results of group A starting point（10，1.5）

观察图13（a）和图14（a）可以发现，A、B两组实验中优化路径的实际路径与理论路径吻合度高；而图13（b）和图14（b）所示，C-L-C路径的实际路径与理论路径之间产生了极为明显的偏离。由图13（c）和图14（c）可知，A组中C-L-C路径的跟踪误差最大值为208 mm，B组中C-L-C路径的跟踪误差最大值为219 mm，两组均超出了泊车时的安全距离Lsafe=200 mm，极易发生碰撞；A组优化路径的跟踪误差最大值为9 mm，B组优化路径的跟踪误差最大值为12 mm。因此，优化路径的跟踪效果明显优于C-L-C路径的跟踪效果。

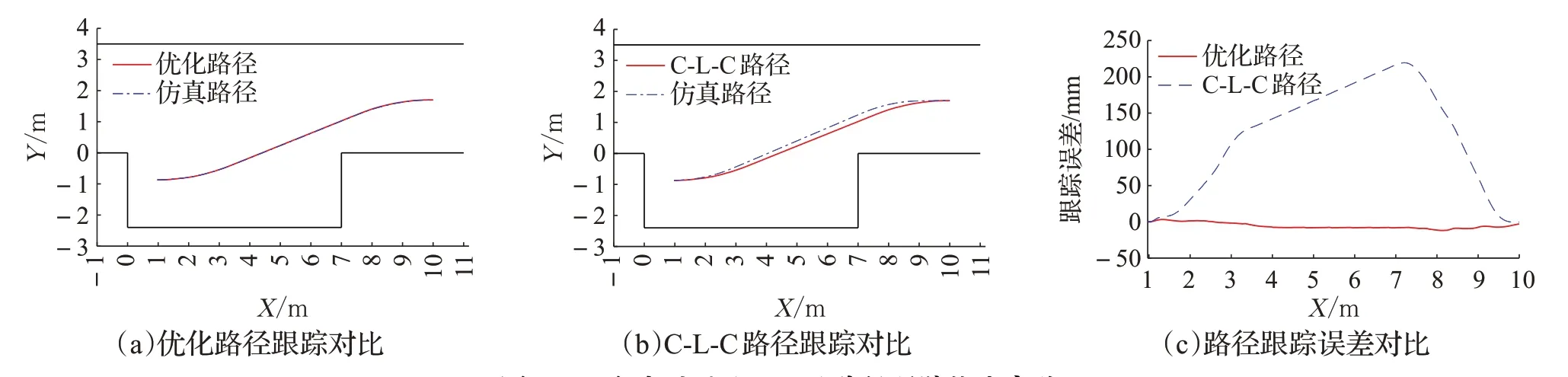
图14 B组起点为（10，1.7）路径跟踪仿真实验Fig.14 Path tracking simulation results of group B starting point（10，1.7）

6 结语

为解决自动泊车路径规划的曲率突变问题，提出了五次多项式优化的平行泊车路径规划方法。使用五次多项式曲线对路径的曲率突变处进行优化，并以“虚圆半径”作为最小转弯半径，按照“C-L-C”平行泊车路径规划的方法进行求解，从而得到优化路径。仿真证明：优化的路径规划方法能够规划出满足避障约束和车辆运动学约束的平行泊车路径，解决了泊车路径的曲率突变问题，从而提高路径跟踪效果，保证平行泊车过程的安全性、可靠性。

虽然优化路径的曲率不会发生突变，但存在小幅度的波动，下一步可对五次多项式的约束方程进行优化，使路径曲率变化更加平滑；后续还将针对狭小车位、垂直车位等场景，对本文提出的路径规划方法进行改进与验证。