融合图特征的多机器人栅格地图拼接方法

黄小杭，曾 碧，刘建圻，汪明慧

广东工业大学 计算机学院，广州 510006

对未知环境构建地图是移动机器人技术中的一项基本挑战，而地图的构建通常需要对机器人位姿的精确估计，因此目前移动机器人主要通过同步定位与建图（simultaneous localization and mapping，SLAM）技术[1-2]构建环境地图，目前已有多种较为成熟的单机器人SLAM算法[3-5]，而在大规模未知环境中，单机器人的地图构建精度、效率和鲁棒性都存在限制，在过去的十年中，多机器人协作已经成为了目前研究的热点，多机器人的引入有助于突破上述单机器人SLAM算法存在的限制。在机器人SLAM算法中，其地图类型可分为特征地图、拓扑地图和栅格地图[1-2]，其中栅格地图可直观地表达真实环境的结构，存储方便，并在精确定位与导航方面更具优势。

在多机器人SLAM中，各机器人在构建各自的局部地图之后，如何拼接局部地图并确定各机器人之间的相对位姿是个热点问题。

Konolige等人指出，机器人地图拼接问题是一个有意义且具有挑战性的问题，但是它并没有像SLAM等其他机器人问题一样受到关注[6]。

其中基于优化和特征匹配的方法是较为主流的思路。Carpin和Brik将地图匹配问题建模为优化问题，然后通过随机搜索算法进行求解[7-8]。在他们的后续工作中通过使用删除异常点的机制和更复杂的方法来优化搜索来提高先前工作的性能[9]。Carpin提出了一种使用Hough变换对搜索空间建模的方法，并将其分解为平移和旋转估计，以合并多机器人系统中的占据栅格地图[10]，该方法拼接速度快，但由于Hough变换存在参数离散化现象，且匹配效果容易受到地图噪声影响，鲁棒性较差。

对于基于特征匹配的拼接方法，其中利用SIFT（scale-invariant feature transform）[11-13]、SURF（speeded up robust features）[14]、PCA-SIFT（principal component analysis-based SIFT）[15]、ORB（oriented fast and rotated brief）[16]等图像特征，将地图视为图像，此时栅格地图拼接可视为图像配准的一种特殊情况。由于室内环境的自相似性，与一般的图像相比，栅格地图提供的特征较少，仅适用于重叠率较大的地图，这些方法容易受到局部最小值的影响，尤其是在没有准确的初值估计的情况下。

地图拼接问题目前主要面临以下挑战：

（1）栅格地图的拼接需要较大的重叠区域。

（2）由于SLAM算法本身存在累积误差和观测噪声，因此构建的地图往往存在一定的非刚性形变。

（3）需要考虑地图拼接的处理时间，尤其是对于大型地图，其计算会非常密集，因此会阻碍某些同时运行的具有实时需求的程序，例如机器人定位和导航程序。

针对上述问题，本文提出通过融合图特征的栅格地图拼接方法，所提出的方法基于ORB特征点，通过建立关特征点之间的中值K近邻图来表征局部关系，建立最优传输模型并求解最优特征点匹配，实现栅格地图鲁棒的配准和拼接。本文方法具备较高的拼接精度，可拼接重叠度较低的地图，且具备一定抗非刚性形变干扰的能力，在本文实验中，本文方法也展现出了较快的计算速度，尤其是在面对大规模场景。

1 栅格地图拼接的问题描述

移动机器人创建的栅格地图，通过将环境划分为等分辨率的平面栅格，这些栅格通过矩阵形式存储于计算机中，可视为图像。假设系统中存在两台机器人A和B，其构建的栅格地图表示为图像IA和IB，其中对于所有像素pij∈I都存在三种可能的状态：占据、空闲和未知。其中未知状态主要受机器人自身观测影响而非真实世界的描述，因此本文将空闲和未知的状态均归为“其他”状态，此时待处理的栅格地图可二值化为两个状态：占据pij=1或其他pij=0，定义两台机器人的栅格地图点集数据为：

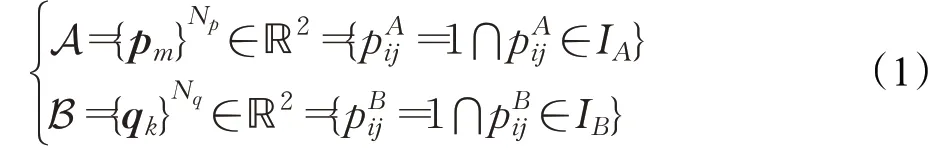
且两者存在重叠区域即A⋂B≠∅，栅格地图拼接问题即求解A到B的刚体变换T={R,t}。其中R∈SO(2)为旋转矩阵，t∈ℝ2为平移向量：

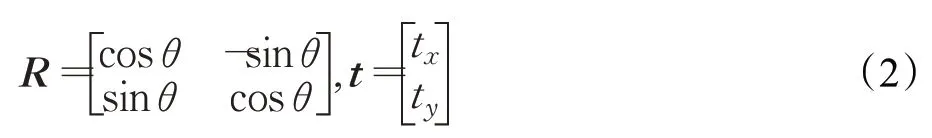
经过变换后点集A与点集B的重叠部分配准，即可进一步将栅格地图拼接表示为如下的最小化问题：

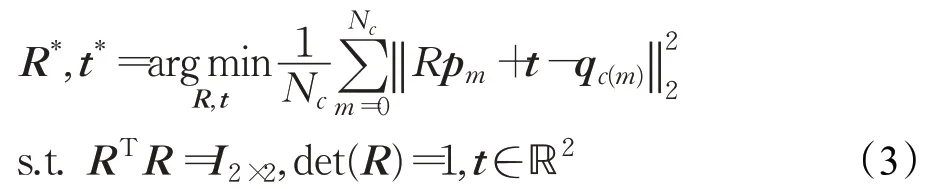
2 融合图特征的栅格地图拼接方法

2.1 ORB特征提取与粗匹配

本文采用ORB[17]特征。ORB是一种FAST特征点检测和BRIEF特征描述符融合的图像特征提取算法，其具有较高精度，较小的计算量，以及良好的旋转不变性和尺度不变性。

ORB特征提取和粗匹配步骤如下：

步骤1利用高斯滤波器对待匹配的栅格地图进行适当的模糊，使二值图像的边缘产生连续平滑的梯度，本文使用尺寸为3×3，标准差σ=1的高斯卷积核。

步骤2提取两张地图图像中具有方向信息的多尺度FAST特征点并采用非极大抑制算法去除Harris响应低的FAST特征点，得。

步骤3以FAST特征点的方向为基准，提取BRIEF特征描述子。

步骤4利用FLANN（fast library for approximate nearest neighbors）库[18]的多探针局部敏感哈希（localitysensetive Hashing，LSH）算法快速搜索两个特征点集中距离最近的匹配点对，同时引入Lowe[11]所提出比率测试方法，剔除不合理的特征点，得到匹配点对，。

经过ORB特征的提取与粗匹配，提前剔除较为明显的误匹配点，降低后续算法的计算规模。

2.2 中值K近邻图的构建

为了度量粗匹配结果的几何关系合理程度，用于优化匹配结果，本文受到Aguilar等人[19]提出的图变换匹配（graph transformation matching，GTM）的启发，通过对每张地图中粗匹配后的特征点构建中值K近邻图，即每个特征点和其满足中值约束条件的最近的K个特征点建立近邻图的边，本文以点集构建中值K近邻图Gp=(Vp,Ep)为例，首先定义一个顶点vi对应于每个点pi，即Vp={v1,v2,…,vnm}，无向边(vi,vj)连接着与pi距离最近的K个邻居pj，并且‖pi-pj‖≤η，其中，η为所有顶点对之间的距离的中间数，即：

K最近邻条件可表达其局部几何结构，而中值约束主要在于过滤由于偏远点引起的结构变形。对待拼接的两张地图特征点分别构建中值K近邻图Gp=(Vp,Ep)和Gq=(Vq,Eq)，本文K值取10。

2.3 最优传输模型优化对应关系

2.3.1 最优传输模型构建

为了融合特征描述子和中值K近邻图的特征，优化特征点间的对应关系，和传统特征点匹配方法不同，本文将ORB特征点之间的匹配问题转换为Gp和Gq的图匹配问题，由此可将该图匹配问题转换为指派问题，假设通过粗匹配后待匹配点集为，经过粗匹配后np=nq,为不失一般性，该指派问题可松弛为最优传输问题[20]并表达为求一个软匹配矩阵P,即可建立最优传输模型：

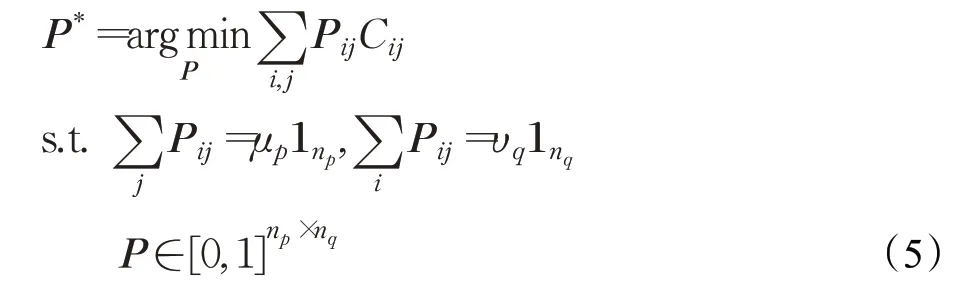
其中，μp和υq表示特征点的总质量，即特征点的权重之和。传输代价矩阵为特征点pi到qc(j)的传输成本，在本文中，特征点权重相等，每个特征点质量可设为1，即：

式（5）中对集合的线性约束确保Vp传递到Vq的质量保持一致，即从集合Vp转移质量到Vq后，系统的总质量保持不变，这就要求此优化问题中Vp和Vq必须具有相同质量，并且每个节点始终以一个质量单位传输，这种情况需要保证最终匹配结果中节点数量np=nq，在实践中可知，由于粗匹配结果中存在无法正确匹配的点对（即离群值），因此传输的质量不一定保持一致。为了移除离群值，同时满足最优传输问题的质量约束，本文引入两个增广节点gp∈Vp和gq∈Vq，用于放置离群值的质量。定义α为离群值权重，用于估计上述最优传输模型中的离群值。增广节点的引入使得式（5）增加了如下约束：

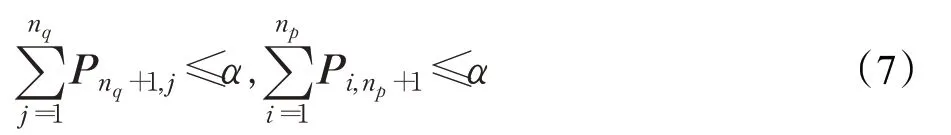
其中：

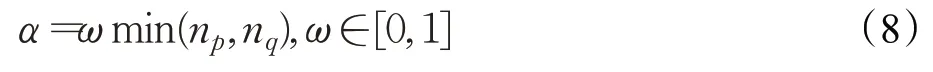
式（8）的参数ω只与离群值的数量有关，可控制离群值筛选的严格程度。为了在求解上述最优传输问题的过程中将离群值吸引至增广节点gp和gq，需要在代价矩阵C中增加关于增广节点传输代价，本文选用C中行或者列的最小值作为其他节点到增广节点的传输代价。在求解该最优传输问题后，所有与增广节点匹配的节点可以认为是离群值，通过从P中删除与增广节点有关的行和列来获得最终的对应关系，示意图如图1所示。

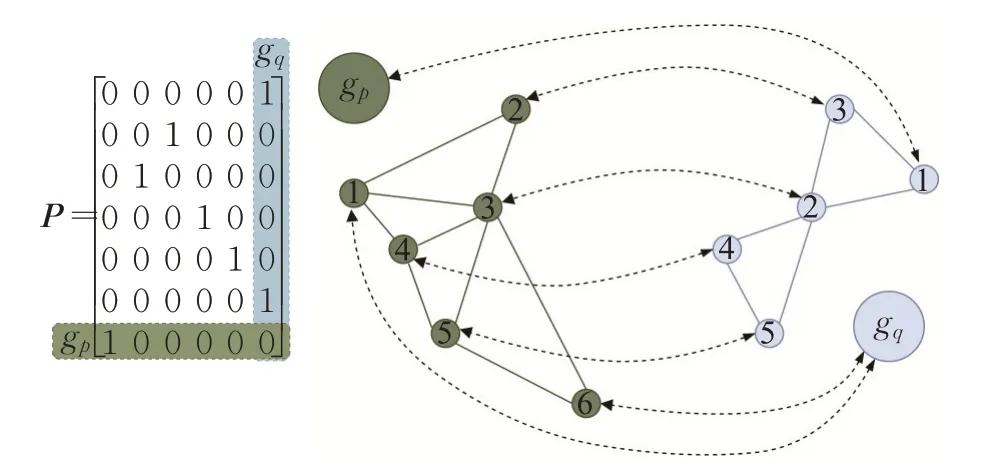
图1 增广节点去除离群值示意图Fig.1 Using additional nodes to remove outliers

2.3.2 最优传输代价矩阵构建

式（5）中的传输代价矩阵C主要由两个部分组成：由Vp和Vq的ORB特征描述子之间的归一化汉明距离构成的节点到节点的相异性矩阵S和表示图Gp和Gq结构相异性矩阵R组成，将代价映射至[0,1)范围内传输代价矩阵可定义为：

其中对于节点结构相异性矩阵R构建，本文对待匹配栅格地图做如下假设：待匹配栅格地图占据点之间的关系约束是保持一致的，因此第一张栅格地图特征点的相邻点对应于第二张地图的特征点的相邻点，若所有对应关系正确，该对节点的邻接结构应保持一致，非正确对应的匹配点将导致两图增加节点间结构相异性。根据这个假设，本文通过计算节点结构相异性矩阵Rij=来度量中值K近邻图的结构相似度，其中Ap和Aq分别为Gp和Gq的邻接矩阵。

2.3.3 最优传输模型求解

待匹配特征点的数量大约在100～2 000这个数量级，若要求式（5）精确解，可利用网络流求解器求解，然而其时间复杂度为O(n3)（其中n与np和nq成正比），时间复杂度较高，因此本文Sinkhorn算法[21]近似求解该最优传输问题，其时间复杂度为O((np+1)×(nq+1))。对式（5）熵正则化：

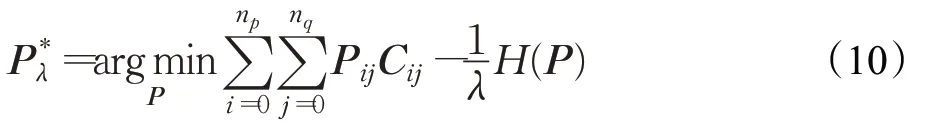
其中：

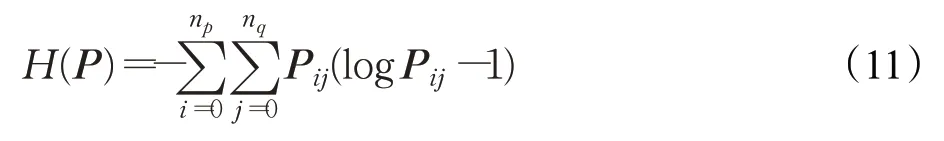
步骤1初始化；

步骤2计算；

步骤3计算P=diag(a)Kdiag(b)并代入式（10）计算Sinkhorn距离ds；

步骤4重复步骤2和步骤3，直到两次迭代的ds之差小于终止条件阈值eps，解得。

2.4 计算拼接结果

2.4.1 变换估计

利用上述方法给出的特征点的对应关系，通过最小二乘法求解式（3）可估计栅格地图IA到栅格地图IB像素之间的刚体变换{R,t}，为了实现较为鲁棒的变换估计，采用随机采样一致性（random sample consensus，RANSAC）算法估计刚体变换参数。相对于传统基于特征点匹配的栅格地图拼接算法而言，本文的特征点匹配关系已经过优化，RANSAC算法仅需较少的迭代次数即可估计精确的刚体变换参数。

2.4.2 地图拼接

创建空白栅格地图IW，栅格地图IA变换为栅格地图T(IA)，其对应像素为：

栅格地图T(IA)和IB均置于空白栅格地图IW，本文采用文献[13]中的融合函数融合对应像素：

其中，x、y分别为栅格地图均为栅格地图的像素值。拼接结果为：

2.5 融合图特征的栅格地图拼接实现

融合图特征的栅格地图拼接方法的具体实现步骤如下：

步骤1输入两张栅格地图图像IA和IB，提取ORB特征并粗匹配。

步骤2构建每张栅格地图特征点的中值K近邻图。首先建立特征点的K维树（KD-Tree），查找每个特征点最近的K个邻居特征点，然后在邻居中筛选出满足中值约束的邻居特征点建立无向边，构建中值K近邻图邻接矩阵Ap和Aq。

步骤3构建最优传输代价矩阵C。分别计算节点相异性矩阵R和图结构相异性矩阵S,代入式（9）计算最优传输代价矩阵C,将C中行或者列的最小值作为其他节点到增广节点的传输代价。设置最优传输权重向量μp和υq,其中特征点节点的权重为均为1，增广节点的权重由式（8）给出。

步骤4将节点权重μp和υq,代价矩阵C和熵正则化系数λ和终止条件阈值eps代入Sinkhorn-Knopp算法中迭代求解软匹配矩阵P,取P每行（或列）最大值的行列索引为节点匹配结果，去除增广节点所匹配的节点后，得到优化后的特征点之间的对应关系。

步骤5将特征点对应关系代入式（3）并通过RANSAC算法估计刚体变换参数{R,t}，创建空白栅格地图IW，地图IA通过式（12）变换后，再通过式（13）所述的融合函数进行像素融合，最后得到拼接结果IW。

3 实验结果

3.1 实验平台、数据集与评估指标

本文方法在一台主频2.5 GHz四核CPU，内存8 GB的笔记本电脑上完成所有实验程序的运行。为了验证本文方法的可行性和性能，并分析所述参数对算法性能的影响，本文主要在TUMindoor数据集[22]和多机器人采集的栅格地图数据集进行实验。

其中TUMindoor数据集采用精度为0.1 m的栅格地图经过人工按一定重叠率裁切，而本文采集的数据集采用图2所示的两台搭载2D激光雷达的微型轮式机器人分别通过Gmapping算法建立栅格地图，所用数据的具体参数如表1，其中T-前缀为TUMindoor数据集，R-前缀为通过多机器人采集的栅格地图数据集。

这里对本文所提出的算法从以下三个方面进行评估：

（1）针对特征点匹配结果，评估算法得出的匹配数，该匹配数由RANSAC算法估计，匹配数可在一定程度上评估特征匹配算法的鲁棒性：当匹配数过低时，经过RANSAC算法估计符合刚体变换规律的特征点较少，故鲁棒性较低；当匹配数足够多时，鲁棒性会相对较好，但过多的匹配数往往会引入假匹配点对和额外的计算量，影响配准精度和运行耗时。可结合后续指标进一步评估。

（3）针对算法实时性的评估，采用算法运行耗时对比的方式评估。

3.2 分析实验

本文方法的匹配数主要受离群值权重ω和正则化系数λ影响，在R-ESAC509数据集中，其参数取值与匹配数的关系如图3所示。

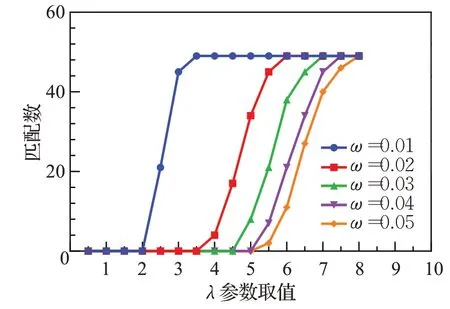
图3 参数ω 和λ 对匹配数的影响Fig.3 Effect of parameters ω and λ on number of matches

可以看出，离群值权重ω取值越大，算法对离群值过滤越严格，若该值过大会导致将正确的匹配归入离群值。熵正则化系数λ越大，算法会尽可能地倾向均匀分配，而该值越小则越倾向于寻找代价最小的匹配，本文的代价矩阵中增广节点的匹配代价最小，因此该值越小过滤离群值的效果越强。在后续实验中，本文选用参数ω=0.02,λ=5。

Sinkhorn-Knopp算法迭代过程中各数据集的Sinkhorn距离收敛曲线如图4。Sinkhorn距离可在4～6轮迭代实现收敛，在工程实现上，直接设定合适的迭代次数而免去Sinkhorn距离的计算可降低迭代计算量。

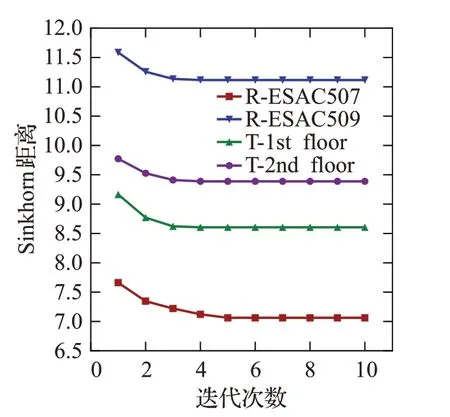
图4 各数据集的Sinkhorn距离收敛曲线Fig.4 Sinkhorn distance convergence curves for each dataset

3.3 对比实验

本文方法将分别与基于SIFT方法和基于ORB方法进行对比，其中鲁棒配准算法均采用RANSAC方法。对比实验数据如表2。图5为地图拼接实验对比，图6为特征匹配结果对比栅格地图。

对于匹配数，基于ORB的拼接方法拥有最高的匹配数，但引入了较多冗余匹配，增加了一定额外计算量。本文算法由于剔除了误差较大的离群值、优化了特征点之间的对应关系，整体匹配数略少，但相对于基于SIFT的匹配方法匹配数量仍然可观，本文算法同时也具有较高的匹配鲁棒性。

对于角度误差和平移误差，本文算法在TUMindoor数据集和多机器人建图数据集均表现出较高的拼接精度和鲁棒性，而基于SIFT的拼接方法在重叠率较低且重叠部分纹理不明显的R-ESAC509中出现配准失误，而基于ORB的拼接方法在数据集R-ESAC507和R-ESAC509中也出现较明显的角度误差。

对于运行耗时，本文算法的平均耗时最短，基于ORB的拼接方法耗时与本文接近，基于SIFT的拼接方法平均耗时最长。尽管在本文算法中最优传输模型的求解部分引入了较多的计算量，但由于该部分如Sinkhorn-Knopp算法主要以矩阵运算为主，且迭代收敛速度快，利用基础线性代数子程序库（basic linear algebra subprograms，BLAS）或GPU并行计算可较为容易地有效提升相关运算速度。在本文实验中仅使用了CPU和BLAS库。

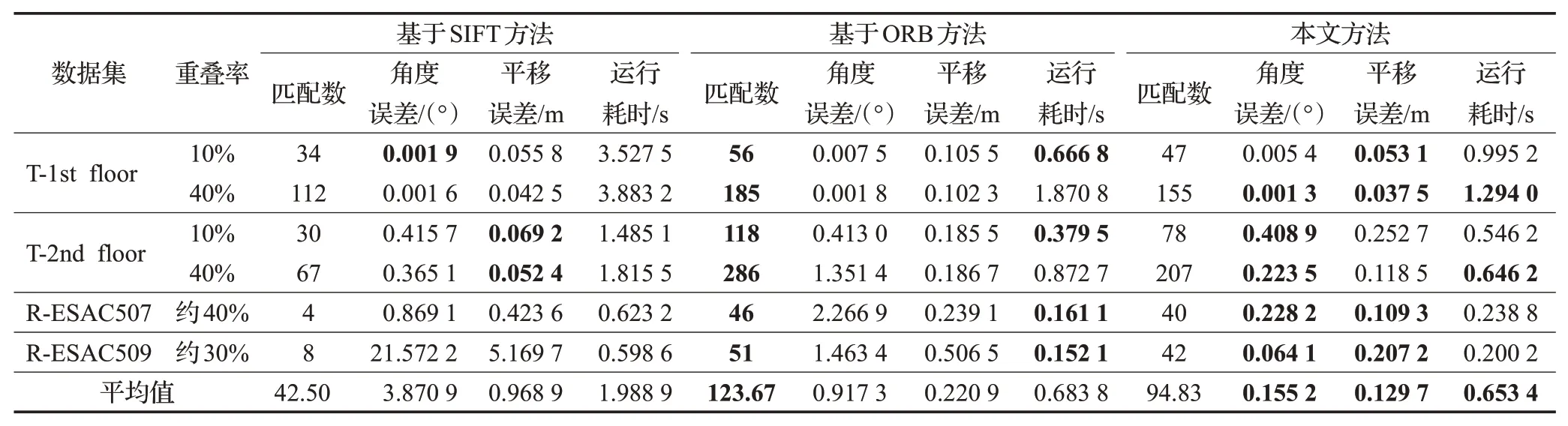
表2 对比实验结果Table 2 Results of comparison experiment

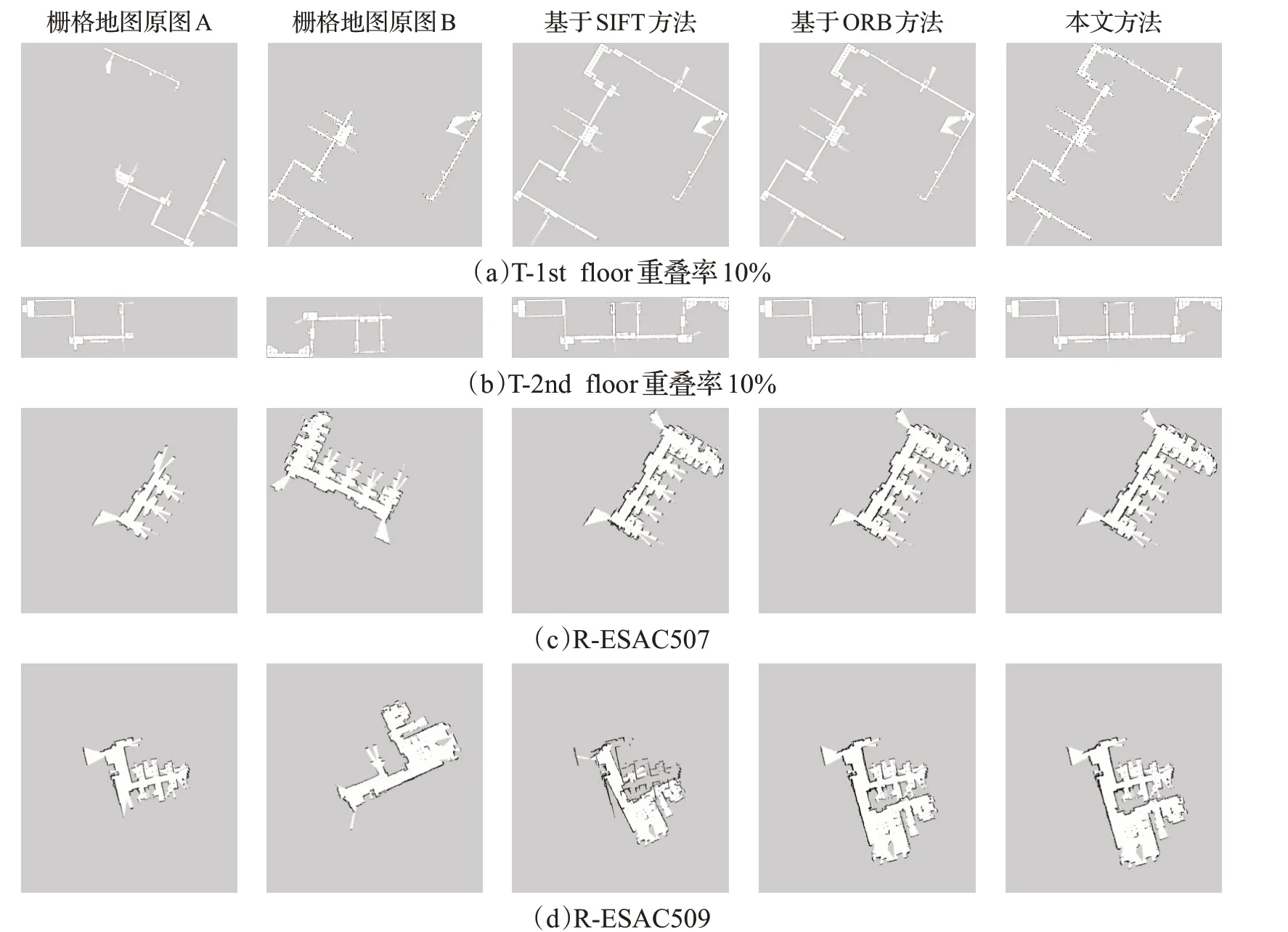
图5 栅格地图拼接结果对比Fig.5 Comparison of results of grid map stitching

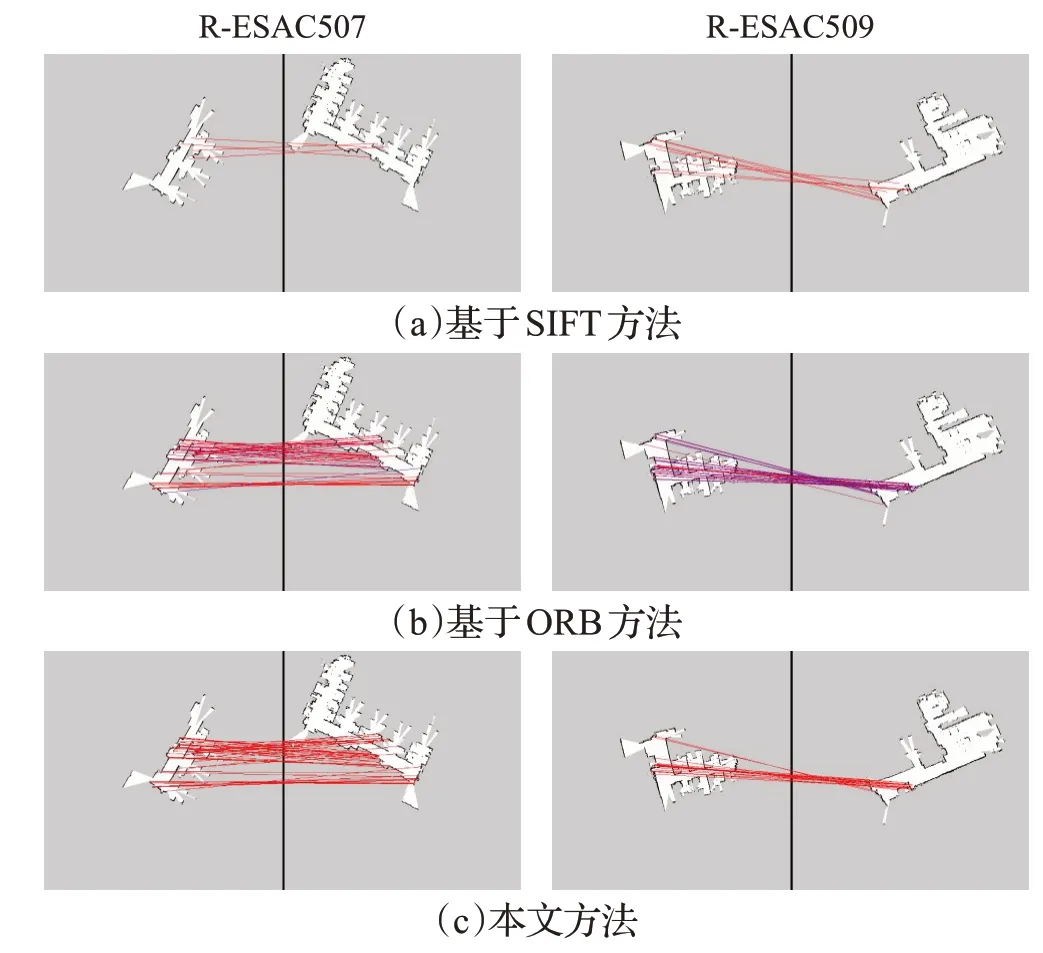
图6 特征匹配结果对比Fig.6 Comparison of feature matching results

4 结论

针对基于特征匹配的栅格地图拼接方法面临的地图特征较少并存在自相似性，依赖栅格地图较大重叠区域、栅格地图存在非刚性形变等问题，本文提出的融合图特征的栅格地图拼接方法，所提出的方法基于ORB特征点，通过建立关特征点之间的中值K近邻图来表征局部关系，并通过最优传输模型求解最优特征点匹配，实现栅格地图的配准和拼接。本文方法具备较高的拼接精度，可拼接重叠度较低的地图，且具备一定抗非刚性形变干扰的能力，在本文实验中，充分分析了相关参数对实验结果的影响，同时本文方法分别与基于SIFT的拼接方法和基于ORB的拼接方法进行了对比，本文方法展现出了较快的计算速度和较高的精度和鲁棒性。