指数平滑与自回归融合预测模型及实证

包研科，陈 然，郑宏杰，冯永安，王 江

1.辽宁工程技术大学 理学院，辽宁 阜新 123000

2.辽宁工程技术大学 智能工程与数学研究院，辽宁 阜新 123000

3.北京泛鹏天地科技股份有限公司，北京 100000

4.辽宁工程技术大学 软件学院，辽宁 葫芦岛 125000

对事物本质的洞察和演化状态的前瞻是正确决策和有效控制的必要条件。随着大数据和人工智能时代的到来，在预测、决策以及系统控制领域，对系统动态指标的在线监控和预测工具的需求持续增加。

对预测理论和技术的研究可以追溯到20世纪初。1927年，数学家Yule为了预测市场变化的规律，提出自回归（autoregressive）模型，标志着时间序列分析方法的产生[1]。至今九十多年的时间，经典的时间序列分析理论与方法已经发展成为一种非常严谨的理论与技术体系。经典的理论可以划分为X-11技术体系和Box-Jenkins方法体系。

1954年，美国普查局的Shiskin首先开发了X-1方法，开始大规模地对经济时间序列进行季节调整[2]。此后，季节调整方法不断改进。1965年发表了X-11方法，该方法基于多次迭代的移动平均法进行成分分解，剔除波动性的影响[2]。X-12方法是在X-11方法的基础上发展而来的，也是基于移动平均法的季节调整方法。X-12方法对X-11方法进行了以下改进[3]：（1）扩展了对贸易日和节假日影响的调节；（2）提出了基于伪加法模型和对数加法模型的季节、趋势循环和不规则要素的分解方法；（3）增加了对季节调整结果稳定性的诊断。20世纪70年代，美国学者Box和英国统计学者Jenkins提出了一整套关于时间序列分析、预测和控制的方法，被称为Box-Jenkins方法，也被称为ARIMA（autoregressive integrated moving average）模型[4-5]。Box-Jenkins方法基于差分技术，剔除趋势特征，再对时间序列进行建模及预测，广泛应用于金融时间序列预测问题[6-7]。1998年，美国普查局季节调整首席研究员David Findley提出X-12-ARIMA方法[8]。X-12-ARIMA方法能够对数据做更加丰富的预处理，检测和修正不同类型的离群值，估计并消除日历因素的影响，对季节调整的效果进行更严格的诊断检验[2]。

近三十年，随着数据科学的发展，特别是人工智能的发展，演化出了基于人工神经网络[9]（ANN）技术和深度学习（DL）的新型预测技术，机器学习（ML）在预测领域得到广泛应用。其中，源于自然语言处理（NLP）领域的循环神经网络[10]（RNN）、长短期记忆（LSTM）循环神经网络[11]、门控循环单元（GRU）网络[12]和脉冲神经网络[13]（SNN）等模型被研究人员引入到时间序列预测应用中，借鉴、改进、融合，服务于管理决策和控制。廖大强等[14]提出多分支递归神经网络学习算法，通过改进一般的BPTT学习算法，对混沌时间序列进行预测。古勇等[15]探讨了循环神经网络在非线性动态过程建模和控制中的应用，提出两步LM算法训练循环神经网络模型，研究了基于该模型的扩展DMC预测控制策略，结果表明控制器的性能得到了很大提高。Ma等[16]考虑时空相关性，提出了一种限制玻尔兹曼机（RBM）与RNN相融合的预测模型，对交通拥堵演变进行建模和预测，在不到6分钟的时间内，预测精度可以达到88%。Zhang等[17]提出一种基于RNN和典型模式发现（RPD）相融合的金融预测策略，对标准普尔500指数（S&P 500 Index）进行预测，结果表明该方法在RNN的基础上最多可提高6%的预测精度，但要以较高的均方误差为代价。王鑫等[18]提出一种基于LSTM的故障时间序列预测方法。黄婷婷等[19]针对金融时间序列预测的复杂性和长期依赖性，提出一种基于深度学习的LSTM网络金融时间序列预测模型。文献[16]虽考虑了时空相关性，但由于梯度消失和梯度爆炸问题的存在，无法处理展开过长的时间序列；罗向龙等[20]针对这一问题提出一种基于K-最近邻（KNN）与LSTM网络相融合的短时交通流预测模型，预测性能得到一定的改善。Liu等[21]提出基于LSTM的银行网点存款准备金预测方法，并成功地将预测系统部署到测试环境中。

GRU模型是LSTM模型简化变体。文献研究表明[22-23]，GRU具有与LSTM类似的性能，但计算速度比LSTM更快。张金磊等[24]提出基于差分运算与GRU神经网络相结合的金融时间序列预测模型，对标准普尔500股票指数进行预测，结果表明该方法能够实现比传统方法（如ARIMA模型）更好的性能，并且具有相对较低的计算开销。Xiuyun等[25]提出一种基于GRU的短期负荷预测模型，在黑龙江省某地区的电力负荷数据上具有较好的预测效果。Hossain等[26]提出一种LSTM和GRU的组合预测模型，实验表明其预测性能优于以往所有的神经网络方法。Jia等[27]提出基于GRU的矿井瓦斯浓度预测模型，随着数据量的增加，与SVR、BPNN、RNN和LSTM模型相比，该模型的时间复杂度更低。

SNN网络以更接近人类神经元工作机理的方式运行，被称为第三代神经网络，往往表现出更好的网络性能[28]。陈通等[29]提出一种基于SNN的光伏系统发电功率预测模型，相对于BP-ANN和SVM预测模型具有更高的预测精度和适用性。

本文的选题，源自北京泛鹏天地科技股份有限公司银行管理会计咨询业务中提出的隔夜头寸预测问题，研究工作始于2019年初。隔夜头寸预测属于金融时间序列一步预测问题，其中各类存款日余额是主要的观测变量。从理论的成熟度讲，马尔科夫链模型应为首选，或者可以选择AR(1)、ARMA(1,k)模型和指数平滑模型。然而，此类模型的应用，一是需要观测变量的大量历史数据支撑，二是依赖观测变量的齐次性或平稳性。由于商业银行业务数据的敏感性，本文的研究工作无法对观测变量的演化特征进行直接的观测和分析，难以直接应用成熟模型及其建模技术。因此，研究团队提出了建立融合指数平滑与自回归模型预测原理的轻启动预测模型的思想路线。所谓“轻启动预测”，指在时间序列预测问题中，不需要对大量的历史数据进行观察和分析、提取时间序列的结构因素和特征，也不需要大量的离线或在线数据对算法进行训练，仅以系统能量变化对序列演化特征的基本影响为先验假设建立一步预测模型，在少量必要的数据支撑下即可启动预测，然后借助滑动窗口技术，实现模型长期在线工作并保持预测的有效性。本文的主要工作包括：提出了EABPs模型并讨论其预测机理，实证分析模型最优启动参数问题，分析了模型预测误差的性质以及序列的波动特征同预测有效性的关系，分析了数据降噪对模型预测性能的影响。

1 EABPs模型

任何系统的发展与波动是系统能量变化的表现。时间序列是一个单变量广义能量系统，预测的不确定性源自外部因素的干扰，表现为系统模型不能恰当地解释系统的所有变化；系统内部的能量变化引起的系统震荡同外部扰动因素造成的不确定性是动态平衡的。基于这样的思想认知，以及参考借鉴混沌时间序列预测的思想原理和技术方法[30]，本文提出了轻启动预测模型。

设x为系统的某个总量指标，假定x(t)是一个二阶矩过程，且至少存在二阶记忆。

所谓对x(t)的一步预测，即以t时刻为预测原点，估计t+1时刻的指标状态，记后验预报误差。

假定Δt=(t+1)-t是一个“小的”单位时间，容易理解，从t到t+1时刻趋势性和周期性因素对x(t)状态变化的解释能力是有限的。因此，对t+1时刻的系统状态进行估计，可以仅考虑t时刻的系统能量变化率和系统发展速率两个因素。本文的观点是：后验预报误差ε(t+1)同t时刻的系统能量变化率正相关，与系统发展速率负相关，即系统因能量的涨跌引发的不确定性受系统演化趋势的抑制。于是，对二阶记忆过程x(t)进行一步预测的微分动力学方程为：

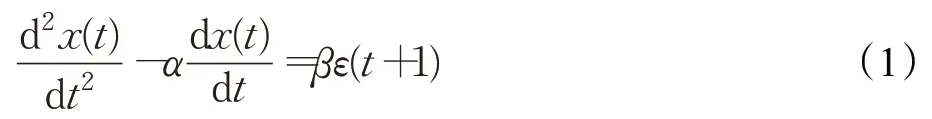
其中，α为系统负阻尼系数，β为系统平衡系数，α＞0,β＞0。

定理微分动力学方程（1）等价于一类无隐层BP神经网络。

证明对微分动力学方程：

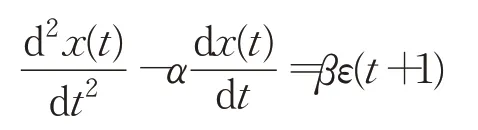
进行有限差分离散化，有：

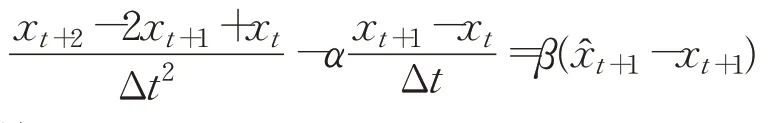
整理得：

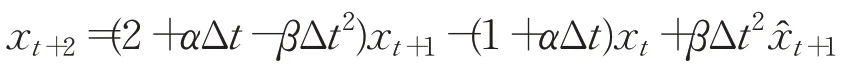
记：

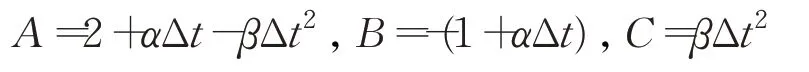
于是，得到递推方程：

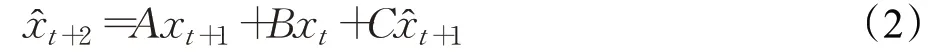
令：

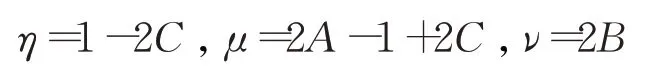
表明递推方程（2）是指数平滑（ES）模型：

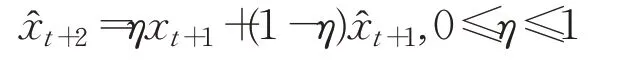
和自回归（AR）模型：

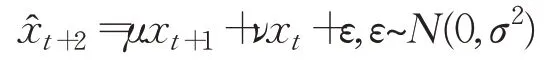
的叠加模型，揭示了微分动力学方程（1）的预测机理。

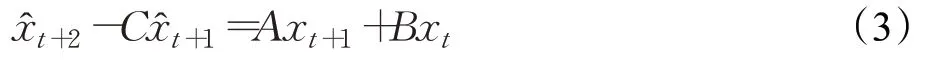
令：

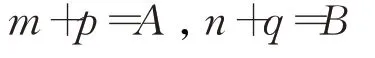
则方程（3）等价于方程组：

即：

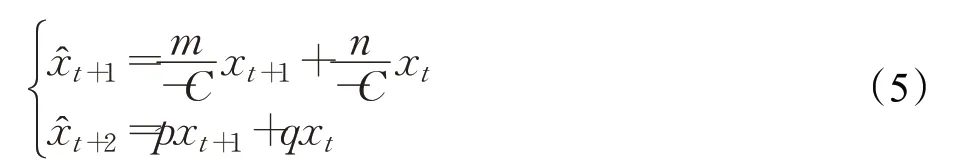
其矩阵形式为：

显然，方程组（6）可表示为一个无隐层BP神经网络：

其中，向量：

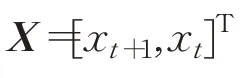
和

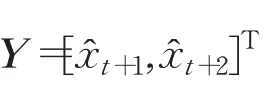
分别为网络输入和输出，b=[b1,b2]T为阈值向量，矩阵：

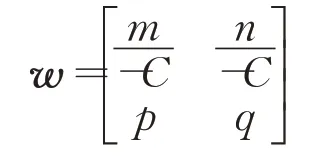
为权值矩阵，f为非线性激活函数。定理得证。

定理的证明过程描述了微分动力学方程（1）同ES模型和AR模型的联系，以及BP神经网络表达和预测应用方法。为后文叙述简便，称由微分动力学方程（1）定义的一步预测模型为EABPs模型（ES和AR模型的融合与BP网络实现），其网络单元结构如图1。

由此可知，本文提出的EABPs模型自身的特点由指数平滑、自回归和BP神经网络模型三者共同决定。

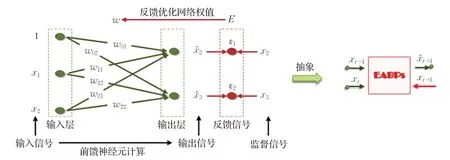
图1 EABPs模型的网络单元结构Fig.1 Network unit structure of EABPs model

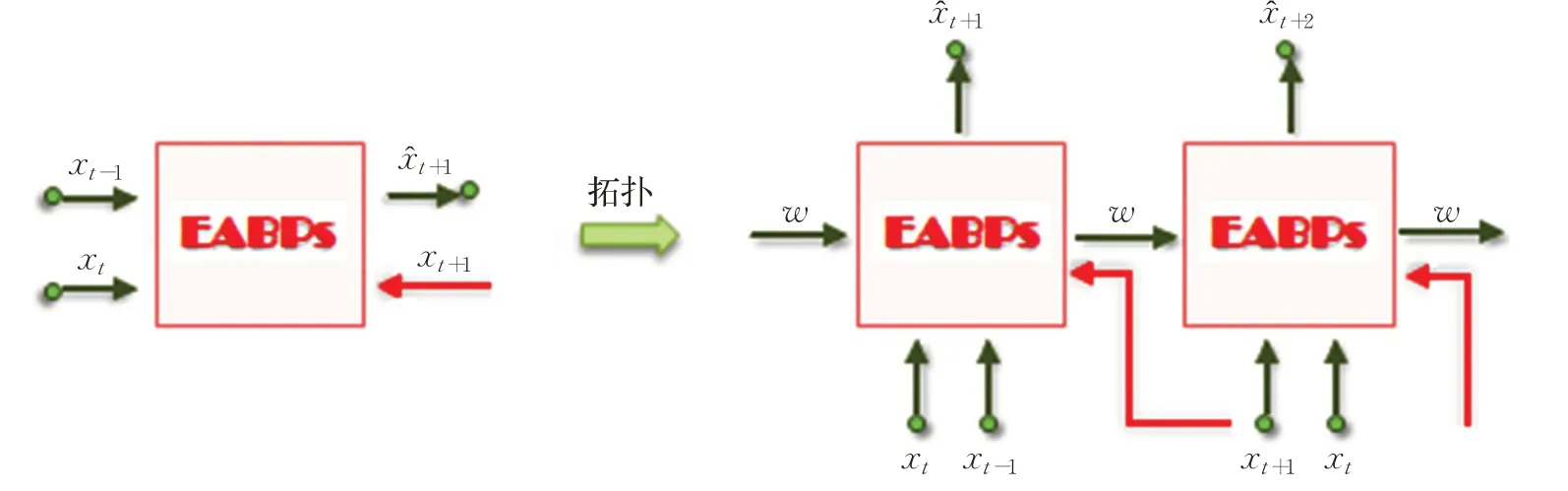
图2 EABPs模型的循环预测机理Fig.2 Cycle prediction mechanism of EABPs model

（1）基于指数平滑模型的预测，理论上是对均值趋势的预测。即在：

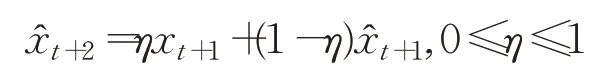
中，通常遵循新值优先的原则[31]，即xt是的最有可能的近似值。显然，指数平滑模型对序列从t到t+1的状态变化不敏感。

（2）自回归模型的参数估计遵循最小二乘规则，因此，基于xt和xt+1预测xt+2时，的期望值在xt与xt+1所确定的直线上：

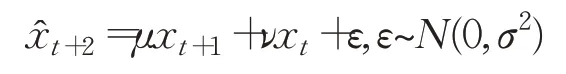
显然，自回归模型对序列从t到t+1的状态变化较敏感。

因此，融合指数平滑模型和自回归模型的预测结果是合理的。在一般情况下，较二者更接近t+2时刻的实际发生值。

（3）前文已经证明了方程（1）同无隐层的BP神经网络等价，则依赖BP算法的自适应性确定融合模型参数，在一定程度上可以平滑模型预报值的过敏反应。

2 EABPs-RNN过程

在应用中，EABPs模型递归使用，形成类似于RNN的结构，如图2。

由图2可知，获得EABPs模型的一个后验预报误差ε需要指标x的3个历史数据，由此构成了模型观测的最小时序窗口，记为e。

由BP算法基于累积误差的“误差反向传递权值修正”原理，可知EABPs-RNN过程的实现需要确定更新权值的时序窗口。因此，设定该时序窗口为由窗口e以单位时间步长连续滑动形成，记为M，如图3。不妨仍以M表示这个窗口的宽度，称为EABPs模型的启动参数。显然，3≤M＜∞。则模型训练次数为M-e+1，即窗口e的滑动次数。

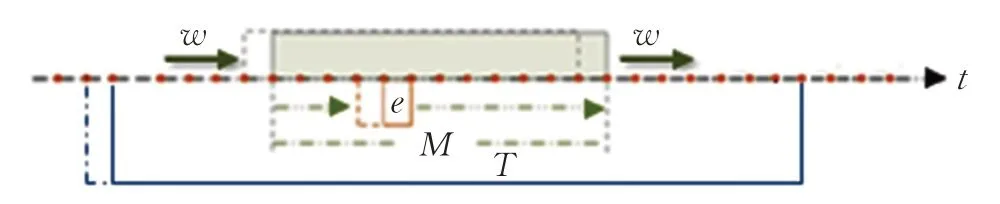
图3 EABPs-RNN过程的计算窗口Fig.3 Calculation window of EABPs-RNN process

2.1 模型训练

下面给出在窗口M上进行模型训练、更新权值矩阵和阈值矩阵的具体计算过程。

步骤1数据预处理

假定以时间t为预测原点，则窗口M中的初始数据向量为：

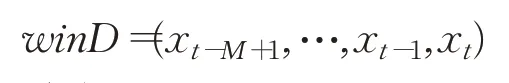
首先，采用min-max归一化对窗口数据wi nD进行处理，以消除不同窗口数据的量级差异。转换公式如下：

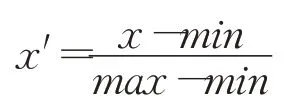
其中，min为窗口数据winD中的最小值，max为窗口数据winD中的最大值。x为原始窗口数据，x′为归一化后窗口M中的数据。

其次，对归一化后的数据进行格式化变换，构造出输入矩阵：

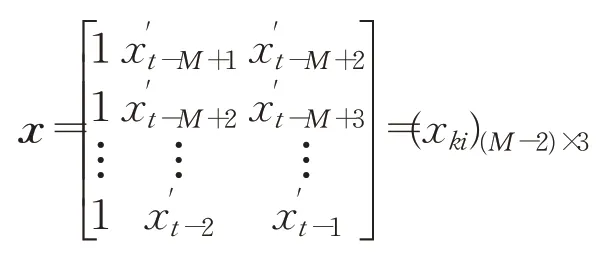
和监督矩阵：

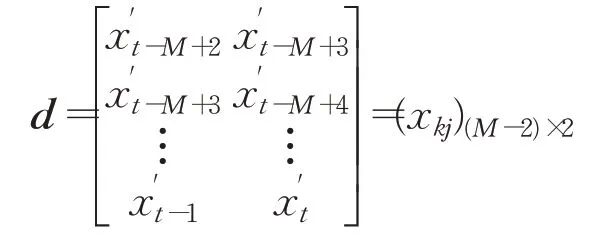
其中，k=1,2,…,M-2表示权值修正需要的最低训练次数；i=0,1,2代表输入节点编号，i=0时代表偏置项1；j=1,2代表输出节点编号。

步骤2正向传递

输出层中第j个节点的输入表达式为：

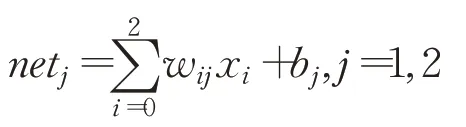
输出层中第j个节点的输出表达式为：

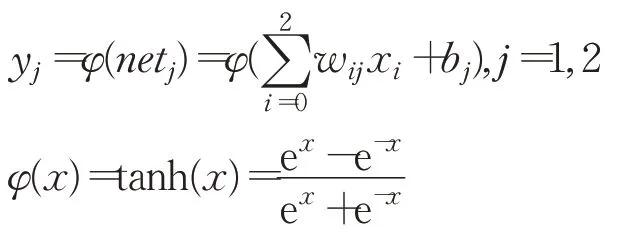
步骤3计算累积误差

步骤4误差反向传递

权值修正表达式为：

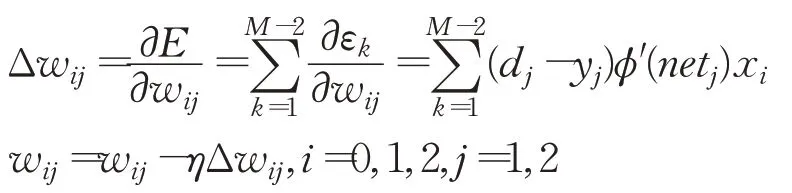
阈值修正表达式：

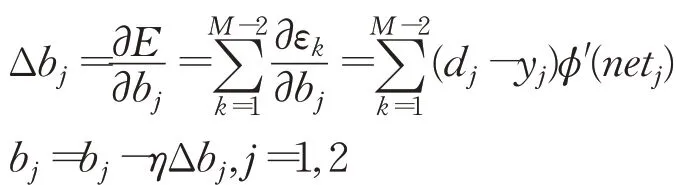
其中，η为最优学习速率。

当累积误差E＜eps（阈值）或达到最大学习次数epoches，则可终止训练。如不满足终止条件，则继续进行模型训练。

2.2 预测过程

训练终止后，提取窗口M中的最后两个数据和，进行窗口M上的一步预测。具体计算过程如下：

步骤1输入数据：

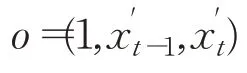
步骤2正向传递。

输出层的输入表达式为：

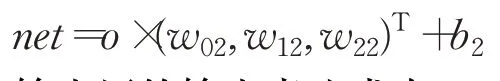
输出层的输出表达式为：

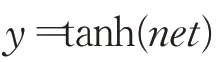
这时，y即为的预测值，又记为。

步骤3由于网络训练时对原始数据进行了归一化处理，因此，需要对进行逆归一化：

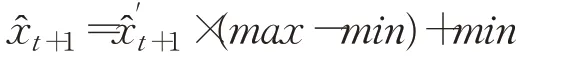
待到第一轮模型训练和预测完成后，将窗口M向前滑动一步，即在窗口M中，淘汰旧数据xt-M+1，添加新数据xt+1，此时窗口数据向量变为：

2.3 模型复杂度

网络模型的复杂度分析包括时间复杂度和空间复杂度。时间复杂度即模型的运算次数，可用FLOPs衡量；空间复杂度即模型的参数数量。

本文模型的创新之处在于，时序长度大于等于M时，便可滚动进行模型训练和预测过程，因此对模型复杂度的分析皆以一个时序窗口为单位进行。

假定网络输入神经元数为Cin，输出神经元数为Cout，下面给出本文模型的时间复杂度和空间复杂度。

（1）时间复杂度

①模型训练

本文讨论的时间复杂度为最坏情况下的时间复杂度，则模型训练的终止条件为达到最大学习次数epoches。故模型训练过程的

又因为输入和输出维数是固定的，Cin=3、Cout=2，则：

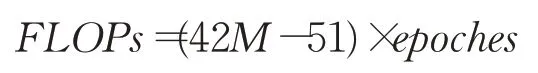
即模型训练过程的时间复杂度为：

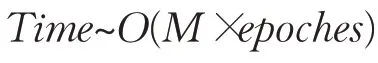
②预测过程

正向传递FLOPs1=2×Cin

激活函数FLOPs2=5

故预测过程的

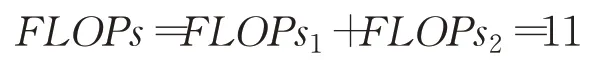
即预测过程的时间复杂度为：

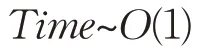
（2）空间复杂度

空间复杂度就是神经网络中待优化参数的个数，即所有的权值w和所有的阈值b的总和。故本文模型的总参数为：

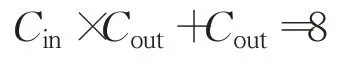
即本文模型的空间复杂度为：

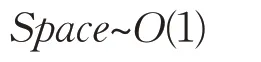
2.4 模型有效性评价

模型有效性评价是机器学习算法研究和应用的重要内容。

本文定义模型有效性评价窗口由窗口M滑动T次形成，不妨记为T，如图3。于是，窗口T的宽度为T+1。在窗口T上，取前T个预测值和与之对应的真实值对预测效果进行评价，然后将窗口T向前滑动一步，用新窗口数据重复进行模型预测效果的评价。

本文主要由预报误差和预报同态性两类指标对模型有效性进行评价。

（1）预报误差本文研究使用平均绝对百分比误差（mean absolute percent error，MAPE），定义为：

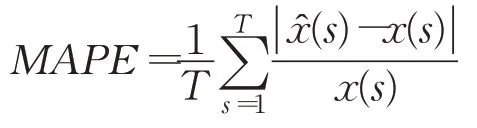
MAPE值越小，模型预报越准确。

在同文献[24]的GRU模型进行比较分析时使用均方根误差（root mean squared error，RMSE），定义为：

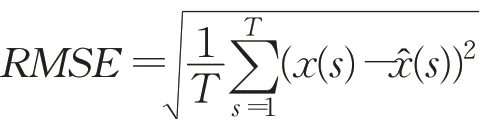
RMSE值越小，模型预报越准确。

（2）预报同态性模型预报的同态度（homomorphism rate，HR）定义为模型预报值的环比指数特征与变量观测值环比指数特征之间相似性的度量：

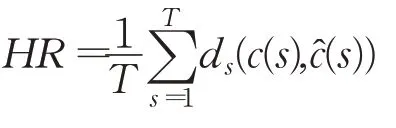
描述预测模型对变量波动态势的跟踪能力，其中：

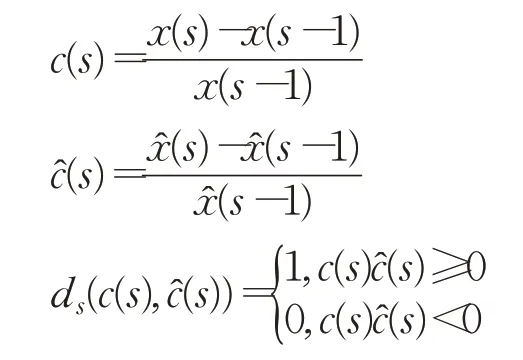
显然，0≤HR≤1。同时，HR值越大，模型对变量波动态势的跟踪能力越强。

模型预报的同态度在有些文献[9]中称为命中率（hit rate，HR）。

3 实证分析

3.1 数据说明

按照时间序列数据的环比中位数大于、等于和小于1，选取了12个样本，用于对本文模型进行实证分析，见表1。

实证分析采用MATLAB自定义程序。

EABPs模型的优化学习速率在0.01～1之间按“预测误差最小”准则实验确定；最大训练次数epoches=5 000，误差阈值eps=6E-10。

3.2 启动参数对预报有效性的影响

EABPs模型的启动参数是“轻启动”的关键指标。

本节考察启动参数M对EABPs-RNN过程预报有效性的影响。实验将M设定为从3到10的八种不同取值，对每一样本根据“预测误差最小”准则确定优化学习速率后，评价模型的预报误差和同态度。同时，基于实验结果给出EABPs模型最优启动参数的参考值。

限于篇幅，仅报告12个样本的中位误差和中位同态度，计算结果见表2。

由表2可知，启动参数M=e=3时，中位误差最小，中位同态度接近最大。

为使观察更加直观，绘制了表2中计算结果的Box图，如图4和图5。

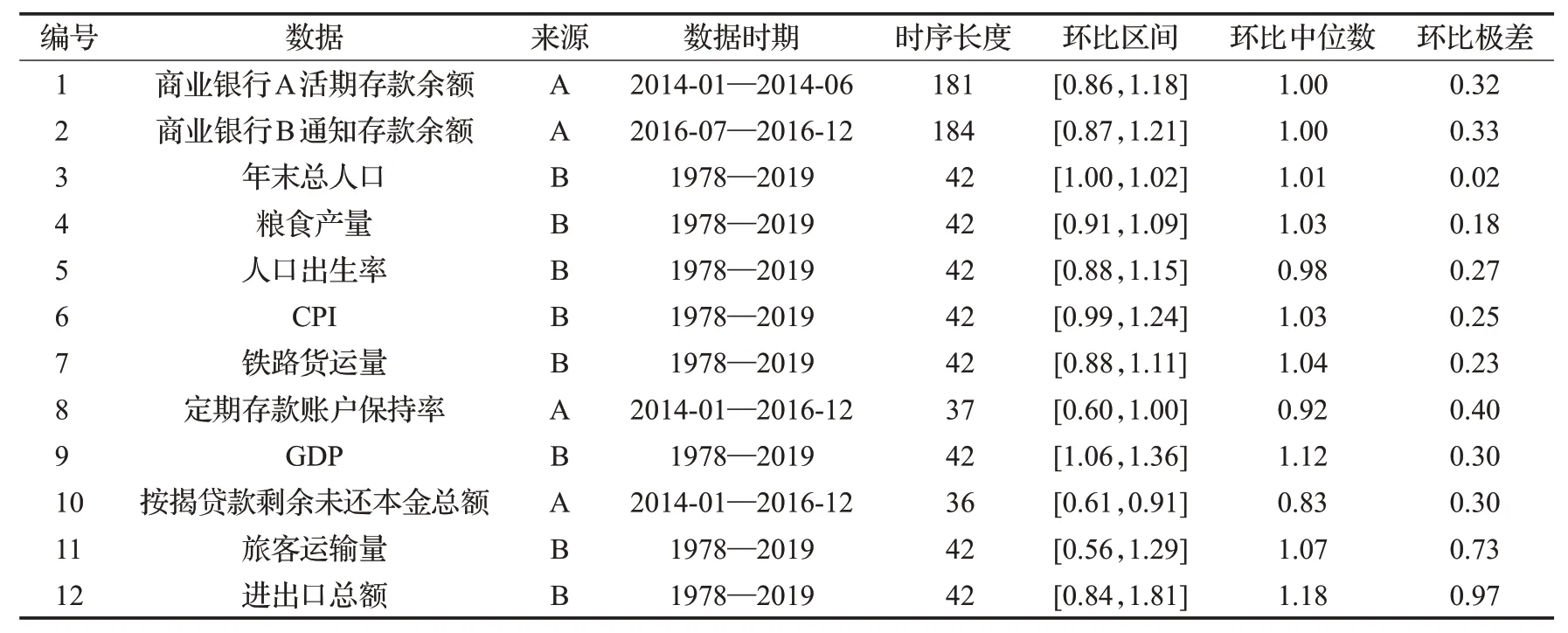
表1 样本数据描述Table 1 Sample data description

表2 启动参数对模型有效性的影响Table 2 Influence of starting parameters on model validity

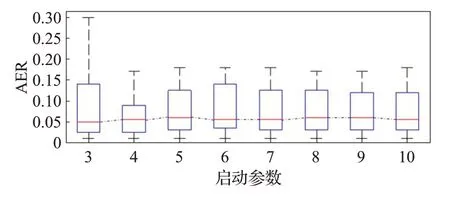
图4 启动参数对预报误差的影响Fig.4 Influence of starting parameters on prediction error

图4表明，启动参数M≥4时，预报误差的变化不大。

图5表明，启动参数M=6是预报同态度变化特征的一个分界点；M≤6时同态度较高，M＞6同态度明显降低。

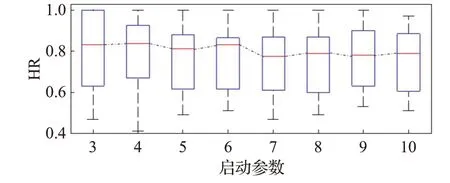
图5 启动参数对预报同态度的影响Fig.5 Influence of starting parameters on homomorphism rate of forecast

综合图4和图5的信息，从模型稳健性的角度看，M=6是最优启动参数的参考值；从本文“轻启动”的预测思想来看，最优启动参数也可选为M=3。

基于上述结果，本文的讨论将在M=3的条件下进行。对表1中12组数据进行预测，其预测结果见图6～17，并通过绝对预报偏差的卡方拟合优度检验结果，分析了EABPs-RNN过程预报误差的性质。

设绝对偏差数据X的概率分布函数为FX(x)，本文假定先验分布为指数分布，则：其中参数θ未知。

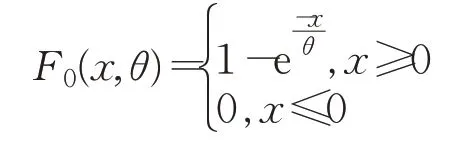
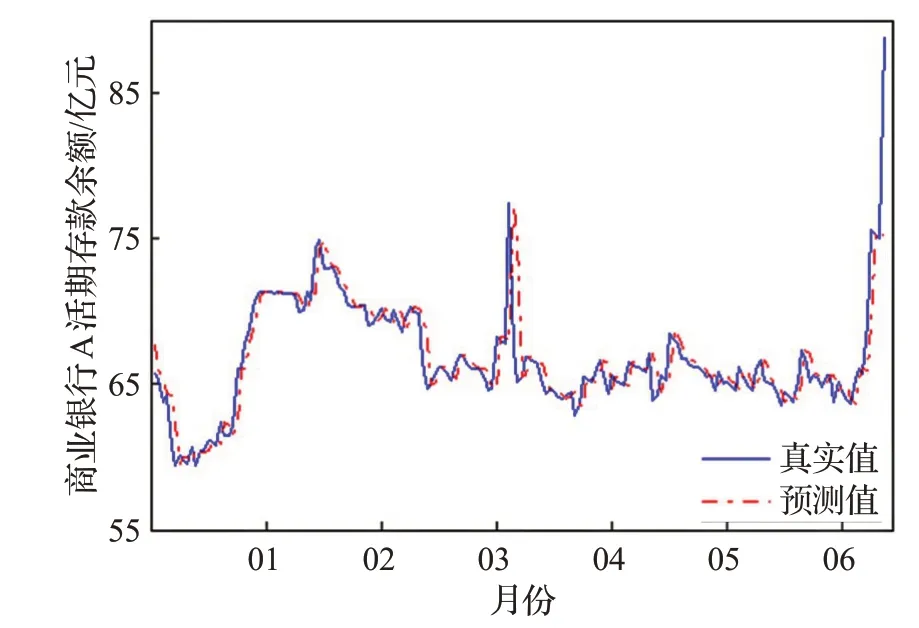
图6 商业银行A活期存款余额数据预测结果Fig.6 Forecast results of current deposit balance data of com-mercial bank A

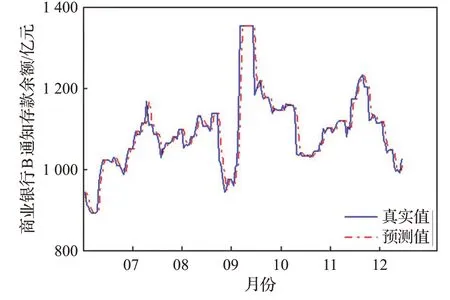
图7 商业银行B通知存款余额数据预测结果Fig.7 Forecast results of call deposit balance data of commercial bank B

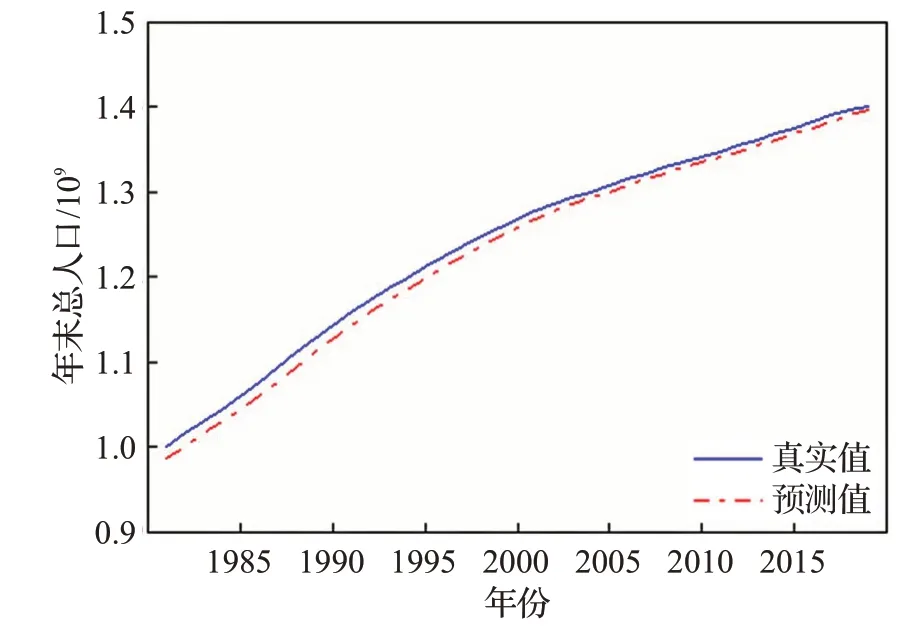
图8 年末总人口数据预测结果Fig.8 Forecast results of total population data at end of year

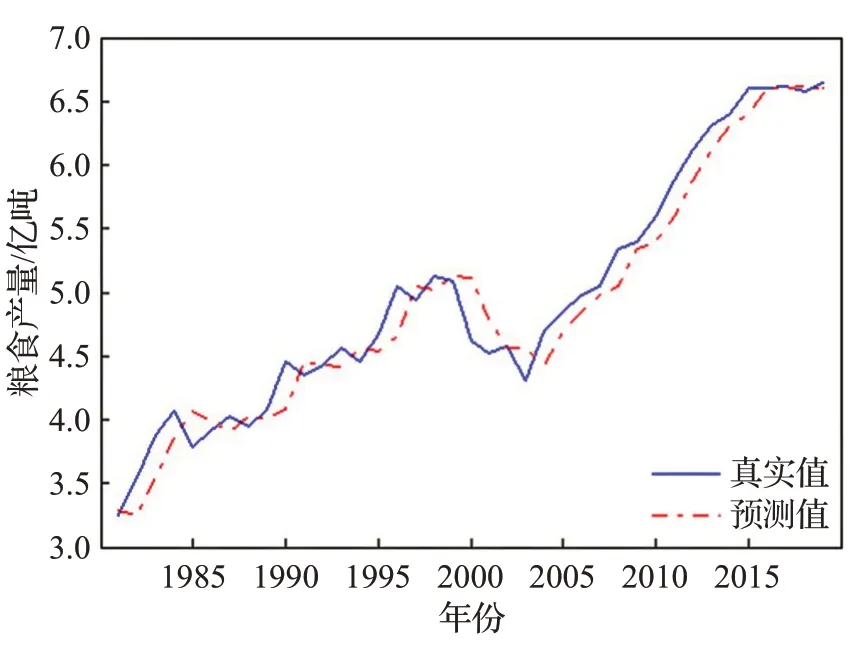
图9 粮食产量数据预测结果Fig.9 Forecast results of grain yield data

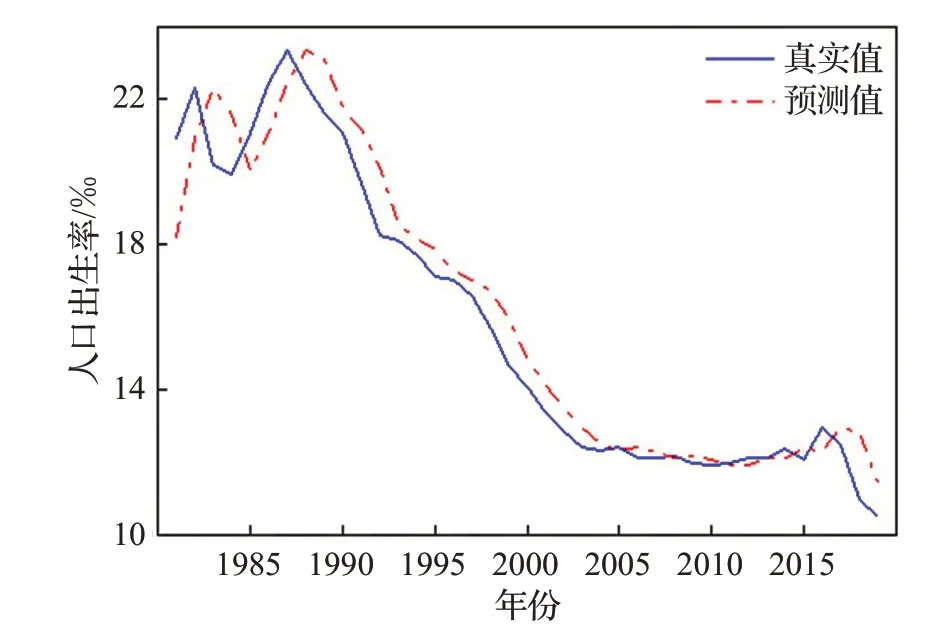
图10 人口出生率数据预测结果Fig.10 Forecast results of birth rate data

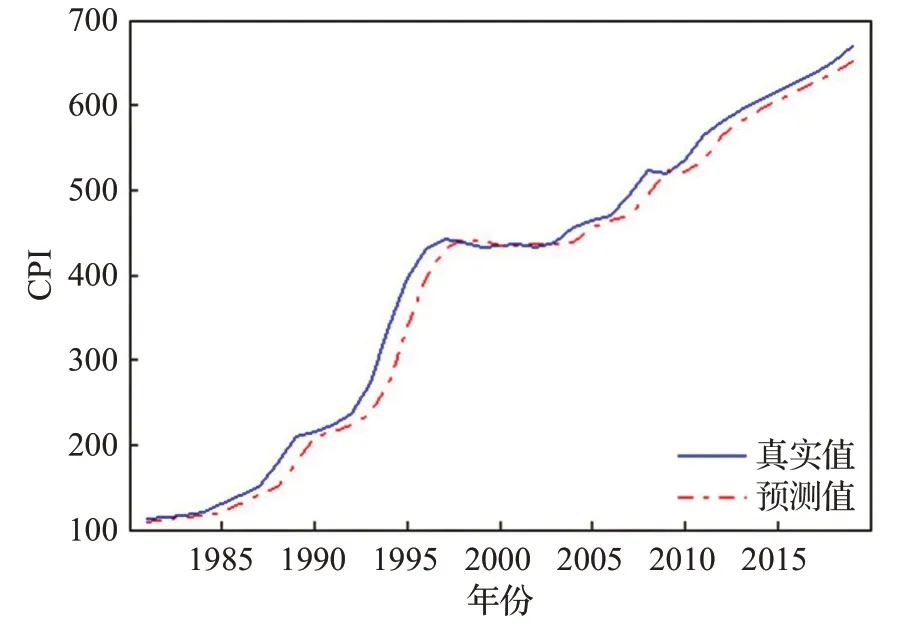
图11 CPI数据预测结果Fig.11 Forecast results of CPI data

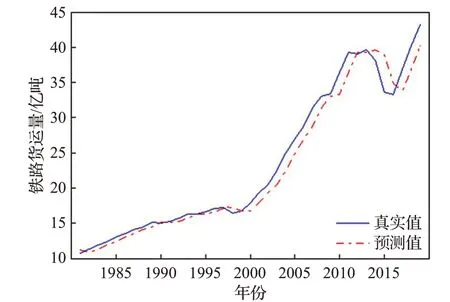
图12 铁路货运量数据预测结果Fig.12 Forecast results of railway freight volume data

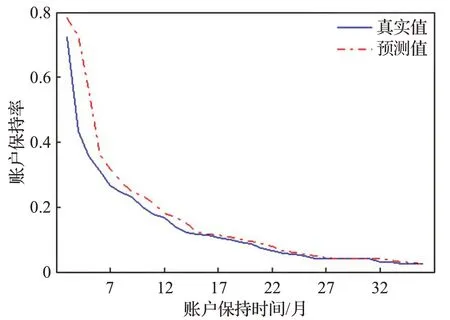
图13 账户保持率数据预测结果Fig.13 Forecast results of account retention rate data

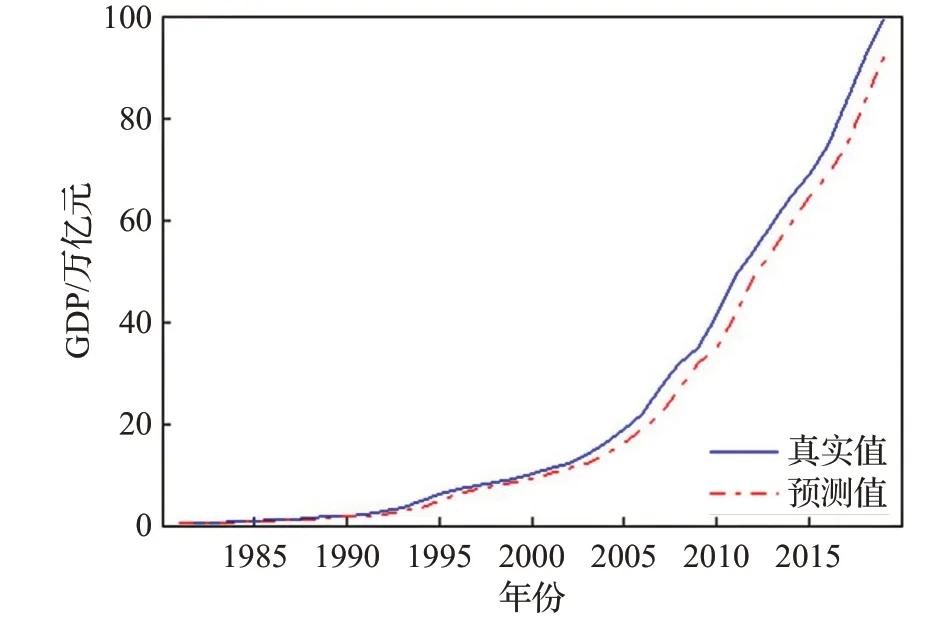
图14 GDP数据预测结果Fig.14 Forecast results of GDP data

在样本数据分组的环节，首先按样本容量的算术根确定组个数进行等距分组，然后遵循小组样本频数大等于5的准则，将不符合条件的小组并入相邻组中；确定分组即组端点后，按标准的卡方拟合优度检验程序进行检验。

检验的计算结果见表3。

由表3可知，在0.01显著性水平下，12个样本的绝对预报偏差的检验p值均大于0.01。考虑到卡方拟合优度检验的结果受数据分组的影响，因此本文的结论是：EABPs模型的绝对预报偏差近似服从指数分布。

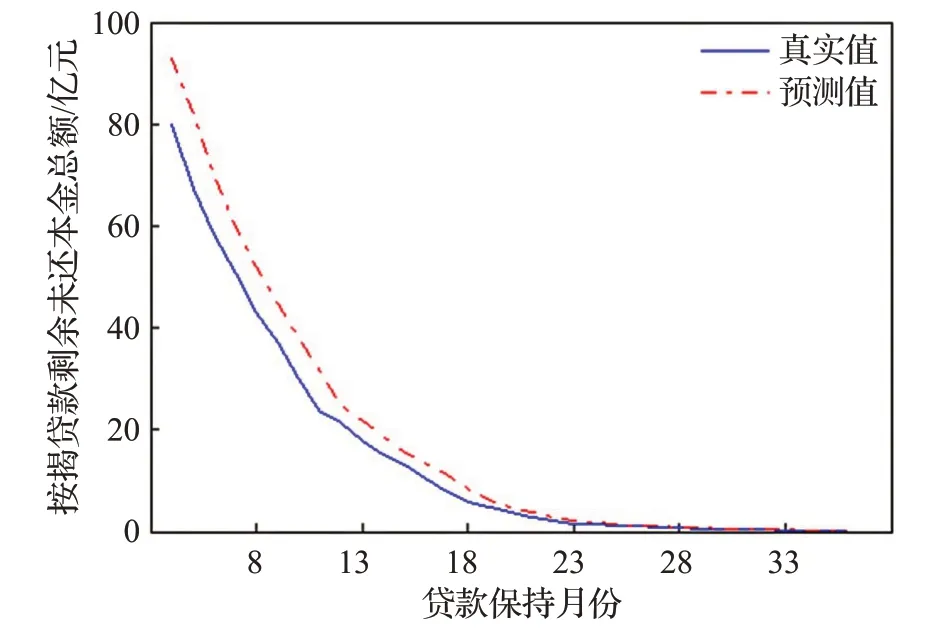
图15 按揭贷款剩余未还本金总额数据预测结果Fig.15 Forecast results of total outstanding principal data of mortgage loan

3.3 数据波动特征与预报有效性的关系

通常，数学模型描述的是变量的变化规律，观测数据的波动是影响模型的有效性的客观因素。

为研究和评价EABPs模型对数据波动的描述和跟踪能力，建立模型适用性的参考知识，本文定义了描述数据波动特征的稳态指数（steady-state index，STI），和转折指数（turning index，TI）。

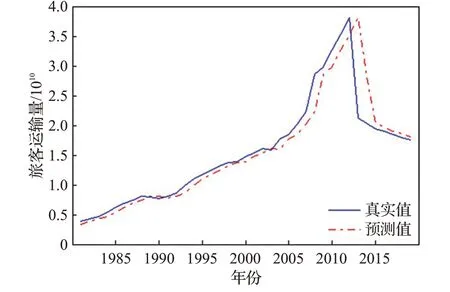
图16 旅客运输量数据预测结果Fig.16 Forecast results of passenger traffic volume data

表3 卡方拟合优度检验结果Table 3 Chi-square goodness-of-fit test results

稳态指数由数据环比指数的中位数及极差度量，即：

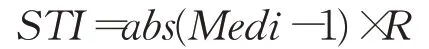
其中，Medi为环比中位数，R为环比极差。

应用中，稳态指数是预判EABPs模型预报误差的工具。

转折指数由数据的转折点在窗口M数据中所占的比例度量，即：

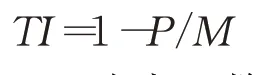
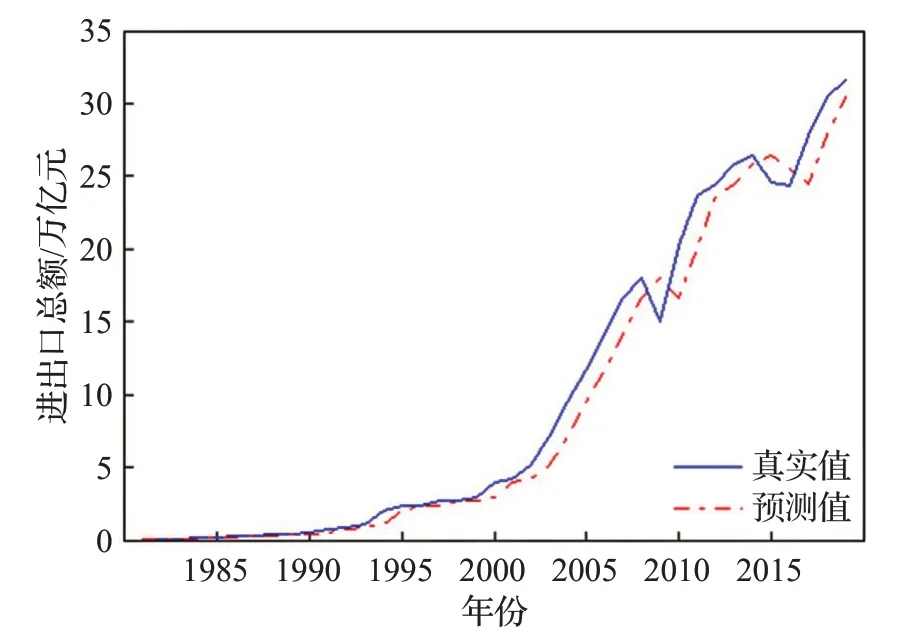
图17 进出口总额数据预测结果Fig.17 Forecast results of total import and export data

其中，P为窗口数据中转折点个数，M为模型启动窗口的数据个数。

应用中，转折指数是预判EABPs模型预报同态度的工具。

表4给出的是在EABPs模型启动参数为3的条件下，学习速率寻优后，一个窗口上模型训练和预测的平均运行时间，即单位运行时间，及稳态指数与预报误差、转折指数与同态度的计算结果。

为使观察更加直观，绘制了表4中数据稳态指数与预报误差的散点图，如图18；绘制了表4中数据转折指数与预报同态度的散点图，如图19。

由图18可知，数据稳态指数与预报误差之间存在近似的混沌分岔特征。分岔[32]就是当参数达到某一临界值时，系统的定性行为发生“质”变的一种现象。

从稳态指数与预报误差的散点图来看，当稳态指数大于0.01时，稳态指数与预报误差的相关关系发生“质”变。即在稳态指数小于等于0.01时，二者基本呈正相关，且预报误差小于等于5%；在稳态指数大于0.01时，二者则不再具有相关性。故，二者的相关关系在S TI=0.01处分岔。

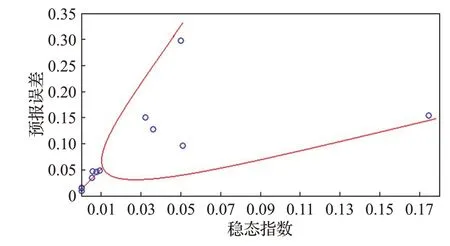
图18 数据稳态指数与预报误差散点图Fig.18 Scatter plot of data steady-state index and forecast error

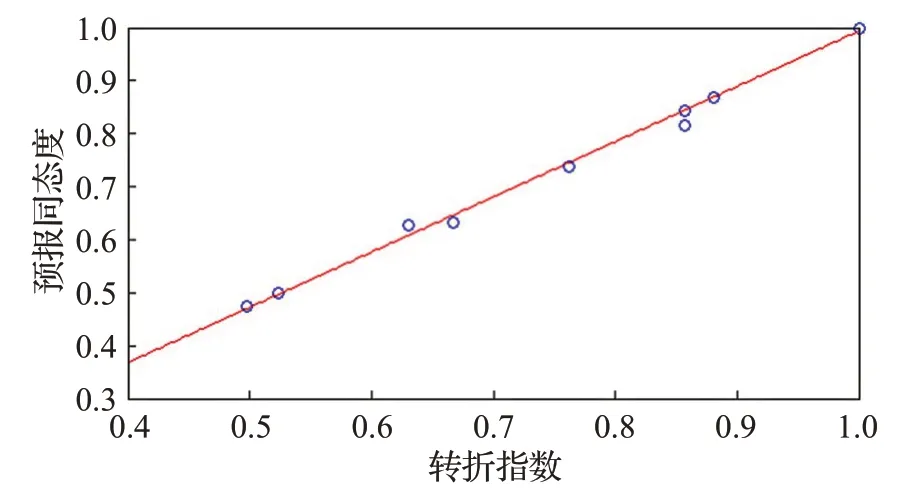
图19 数据转折指数与预报同态度散点图Fig.19 Scatter plot of data turning index and homomorphism rate of forecast

因此，稳态指数可以作为EABPs模型适用性的预估指标，当STI≤0.01时，模型的预报误差基本上可以控制在5%以内。

由图19可知，转折指数与预报同态度呈正相关，且基本相等。因此，由转折指数可预判EABPs模型预报同态度的取值水平。

限于篇幅，由稳态指数和转折指数预估EABPs模型预报有效性的方法，本文不做展开讨论。

3.4 前端滤波对预报有效性的影响

通常，在数据变异的平稳性受到质疑时需要进行数据降噪处理，以抑制模型与算法对大噪声或异常波动产生“过敏”响应。数据平稳波动时，数据的环比指数在1附近一定范围内变化，极差相对较小。由图18的分析可知，当稳态指数STI≤0.01时，EABPs模型的预报误差相对稳定在5%以下，预报效果较好。当STI＞0.01时，数据环比特征对EABPs模型预报误差的解释作用降低，此时，在EABPs模型的前端引进数据降噪过程，虽不能降低预报的误差整体水平，但可以在一定程度上抑制由于数据较大波动引起的模型预报行为的“过敏”响应。

为衡量模型预报行为的“过敏”响应程度，本文定义了预报畸变率（distortion rate，DR）：

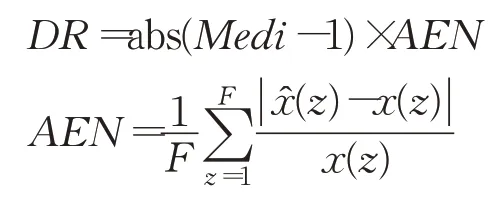
其中，x(z)和分别为时对应的真实值和预测值，即AEN为非同态点的平均预报误差。

对比滤波数据的预报畸变率和原始数据的预报畸变率，如果DR值减小，则说明加入前端滤波后，抑制了模型预报行为的“过敏”响应。

本文采用的数据滤波算法是移动平均算法的一种变式，不妨称为重标记均值平滑算法，同EABPs-RNN过程融合，成为前端自动化的数据处理过程。

在模型启动窗口M上对原始数据进行N项平滑，降噪计算窗口为[1,N](a)，a=1,2,…,N为窗口编号。不妨称N为噪声抑制参数，其中，M=2N-1。

记窗口[1,N](a)中数据为。

降噪计算步骤如下：

步骤1计算N个降噪窗口的数据的均值：

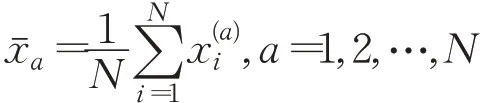
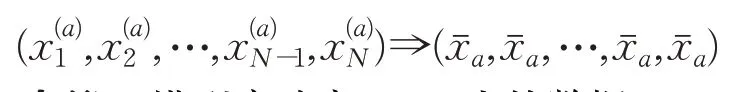
步骤2模型启动窗口M中的数据：

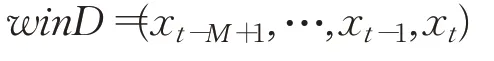
逐点求N重标记的均值，得修匀数据：

其中：

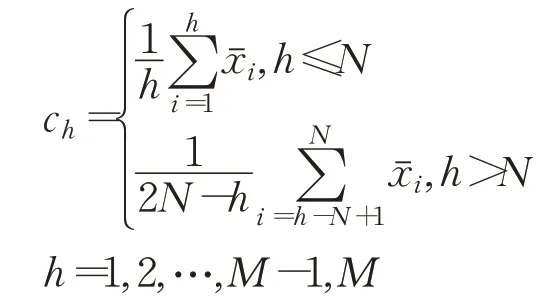
由表3，对STI＞0.01的5个编号为8～12的样本进行前端除噪。

在模型启动参数M与噪声抑制参数N的匹配实验中发现，当启动参数M=3，噪声抑制参数N=2时，5个样本模型预报结果的中位误差为0.19最小，中位同态度为1最大。

因此，计算5个样本在M=3,N=2的条件下，模型预报结果的畸变率，结果见表5。

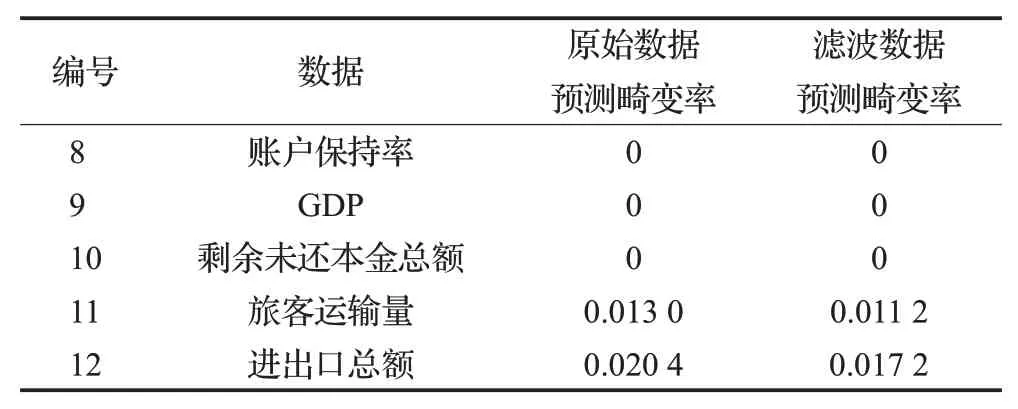
表5 前端滤波对模型预测畸变率的影响Table 5 Influence of front-end filtering on model prediction distortion rate

显然，加入前端滤波后，预测畸变率明显下降，即模型的“过敏”行为得到有效改善。其中，编号为8、9和10的样本数据，滤波前后的预测畸变率均为0，观察图13、14、15，发现这三组为强趋势数据，即数据始终处于上升或下降的状态，且趋势明显增强。

由图13、14、15可以看出，对于强趋势时间序列，EABPs模型的预报有一定的系统性偏差；由偏差绝对值近似服从指数分布，不难建立系统性预报偏差的矫正模型；限于篇幅，本文对此不作展开讨论。

3.5 EABPs模型同LSTM、GRU模型的对比实验

3.5.1 与LSTM模型的对比实验

文献[19]中，黄婷婷等提出了基于深度学习方法的LSTM神经网络预测模型（SDAE-LSTM模型）。首先，利用堆叠去噪自编码从金融时间序列的基本行情数据和技术指标中提取特征，然后，将其作为LSTM神经网络的输入对金融时间序列进行预测。文献[19]中的实验数据为源自雅虎财经官网的香港恒生指数HSI（Hang Seng index）日调整后收盘价数据（2002-01-02—2014-12-31）。

在SDAE-LSTM模型中，SDAE自编码的层数为4，每层的神经元个数分别为16、8、8、8，LSTM层数为2，LSTM隐藏层神经元个数分别为8、8，训练的时间步数为10，即构造的输入序列的长度为10，batch_size为50，即每50个样本更新一次网络参数，训练次数（epoch）为1 000。同时，采用平均绝对百分比误差对模型的性能进行评价，并与文献[33]中的WNN和WPCA-NN预测方法的MAPE值进行比较。其中，WNN、WPCA-NN和SDAE-LSTM模型的平均MAPE值分别为15.5%、4.1%和1.1%。显然，SDAE-LSTM模型的性能优于WNN和WPCA-NN。

为了对比EABPs与LSTM模型的性能，本文用文献[19]中的HSI数据对EABPs模型进行训练并滑动窗口滚动预报。

EABPs模型的启动参数设置为3。本文没有重构文献[19]的模型训练和预报过程，采用同文献[19]一致的模型预报误差评价指标，对预报结果进行评价，评价结果见表6。

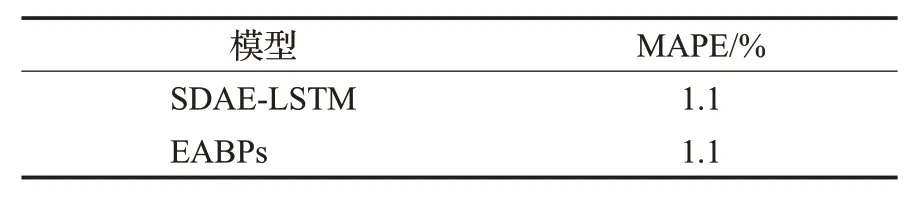
表6 EABPs与LSTM模型的性能比较Table 6 Performance comparison between EABPs and LSTM models

由表6可知，本文EABPs模型的MAPE计算结果为1.1%，与LSTM模型的MAPE值相同。

但是，LSTM模型的网络结构显然相对复杂，模型训练需要大量历史数据；而EABPs模型的网络结构单元仅为无隐层BP神经网络，轻启动无需对大样本数据集进行训练。

3.5.2 与GRU模型的对比实验

文献[24]中，张金磊等提出了基于差分运算与GRU神经网络相结合的金融时间序列预测模型。首先，对金融时间序列进行差分操作，然后，将处理后的数据输入到GRU神经网络进行预测。

文献[24]中的实验数据为源自雅虎财经官网的标准普尔（S&P）500股票指数日调整后收盘价数据（1950-01-03—2018-03-14）。

文献[24]中采用均方根误差RMSE对模型的性能进行评价，并与文献[34]中的ARIMA模型的RMSE值进行比较。其中，ARIMA和GRU模型的平均RMSE值分别为55.30和15.12。显然，GRU模型的性能优于ARIMA。

为了对比EABPs与GRU模型的性能，本文用文献[24]中的S&P500数据对EABPs模型进行训练并滑动窗口滚动预报。

EABPs模型的启动参数设置为3.本文没有重构文献[24]的模型训练和预报过程，采用同文献[24]一致的模型预报误差评价指标，对预预报结果进行评价，评价结果见表7。

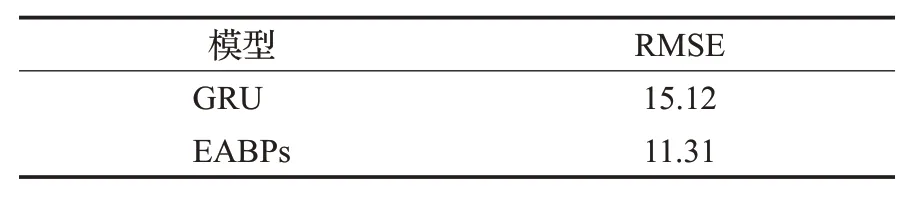
表7 EABPs与GRU模型的性能比较Table 7 Performance comparison between EABPs and GRU models

由表7可知，本文EABPs模型的RMSE结果为11.31，与GRU模型相比，降低了25.2%。同时，文献[24]中提到，GRU模型需要训练781个参数，而EABPs模型只需训练8个参数。更重要的是，GRU模型的网络结构较EABPs模型复杂得多。

故综合表6和表7的结果，在一步预报问题中，EABPs模型比LSTM模型和GRU模型更为适用。

4 结语

综上讨论，对本文的工作总结如下：

（1）本文研究创新性地提出了基于微分动力学方程（1）的EABPs模型以及EABPs-RNN预报过程。实证分析表明，EABPs模型具有明确的“轻启动”性质，网络结构简单，有一定的预报可靠性。EABPs模型随泛鹏天地的业务活动在国内某商业银行的试用结果表明，在隔夜头寸预报中表现良好，能够为业务决策提供有效的参考信息。

（2）本文创新性地提出了稳态指数、转折指数，为分析数据的环比波动特征和模型预报有效性之间的关系提供了一种思想方法，可供同类研究参考。

（3）本文基于几何学思想原理改进了移动平均滤波算法，创新性地提出了畸变率指标，为度量和评价前端滤波对模型预报结果的影响提供了可参考的技术方法。

（4）实证分析表明，EABPs模型的绝对预报残差近似服从指数分布，发生大预报误差事件是可控的；在稳态指数STI≤0.01，可以预估模型预报的误差水平，这时平均绝对百分比误差可以控制在5%以内；由转折指数可以预估模型预报的同态度。对于稳态指数STI＞0.01的时间序列，模型前端降噪可以抑制模型预报的“过敏”行为，能够更好地描述序列的趋势规律。

（5）同NLP框架下的LSTM模型和GRU模型的对比实验虽不充分，但同文献[19]和文献[24]的比较分析结果表明，EABPs模型在时间序列短期预测问题中有更好的表现。

限于篇幅，本文仅讨论了EABPs模型一步预测问题；项目组研究了基于EABPs模型的多步预测问题，方法和结论另文报告。