融合网格划分和DBSCAN的改进聚类算法
2022-07-21梁永全
孙 璐,梁永全
山东科技大学 计算机科学与工程学院,山东 青岛 266590
近年来,信息技术的快速发展使得可用数据爆炸式增长,数据分析在现实生活场景中的应用范围不断被拓展,这对数据分析技术的精度和效率都提出了更高的要求,如何对大规模数据集进行快速、有效的分析和处理变得越来越重要。聚类是一种重要的数据分析技术,是最早研究空间数据集中数据结构和模式的数据挖掘技术之一[1-2],在图像分析[3]、模式识别[4]、知识发现[5]和生物信息学[6]等多个学科领域具有一定的应用价值。随着国内外研究人员对聚类算法研究的不断深入,产生了许多优秀的算法。根据算法实现原理和探究方向不同,目前五种主流的聚类算法为基于划分的方法、基于密度的方法、基于层次的方法、基于网格的方法和基于模型的方法[7]。
DBSCAN是最经典的基于密度的聚类算法之一,其根据数据集的空间分布密度对样本点进行聚类,可以在有噪声的数据中发现任意形状的类簇[8-9],在真实应用场景中处理复杂数据时算法性能优越,得到了国内外学者的广泛关注。然而,DBSCAN算法也存在一些缺陷:(1)采用全局参数导致其在密度不均匀数据集中的聚类质量不高;(2)采用暴力破解法为每个样本点计算邻域密度,计算复杂度较高[10],传统DBSCAN算法在最差情况下的时间复杂度为O(n2),在运行时间为O(nlogn)时,随着数据集的维度或者规模的增加,平方级的时间开销逐渐显现[11],这极大地限制了其在大规模数据集中的应用。近年来,很多学者从不同角度针对这些问题做出了改进。文献[12]通过确定密度峰值点来自适应地选择聚类的局部半径,并据此扩展密度峰值点进行聚类,提高了聚类结果的质量。文献[13]通过贪心策略自适应确定局部最优邻域半径,并通过比较邻域内点之间的平均距离与半径参数发现噪声,提升聚类精度。文献[14-15]通过减少为数据集中每个点计算邻域密度时的冗余计算量,提高算法执行速度。文献[16-17]通过选择几个代表性的核心点作为种子来扩展类的方式,减少重复的邻域检索,加快聚类。文献[18-20]利用图形处理单元(GPU)、空间分区数据结构(如R树和KD树)或并行算法提出了基于密度的快速、可扩展的聚类方法,用于处理大型数据集。这些方法都在一定程度上提升了DBSCAN算法的性能,降低了算法的时间复杂度,但是这些方法大多无法较好地兼顾时间开销与算法性能。
DBSCAN算法中存在大量无用的距离计算,可以通过减少这些无用计算来降低算法的时间复杂度。基于此,本文提出了一种网格聚类与DBSCAN相结合的融合聚类算法(G_FDBSCAN),使用网格划分技术将数据集划分为密集区域和稀疏区域,分而治之,既缓解了全局参数导致DBSCAN算法在密度不均匀数据集上的聚类精度不佳问题,又显著降低了算法的时间复杂度,同时还可以在一定程度上解决网格聚类受网格划分参数影响较大,只能发现边界是水平或垂直的簇而不能检测到斜边界的问题。
1快速DBSCAN算法(fast DBSCAN,FDBSCAN)
1.1传统DBSCAN聚类算法
传统DBSCAN算法将簇定义为由非密集区域间隔开的密集区域的集合。如果用欧几里德距离作为相似性度量,这些密集区域是以给定点p为中心以ε为半径的超球体。假设有n个d维F分布的i.i.d.样本点的集合X={x1,x2,…,xn}。根据DBSCAN的两个超参数:核心点的邻域半径ε和密度阈值δ,给出DBSCAN的一些相关定义。
定义1(ε-邻域)对于样本点p∈X,其ε-邻域是样本集X中与p的距离不大于ε的样本点集合,即Nε(p)={q∈X:|p-q|≤ε}。
定义2(核心点)对于任意样本点p∈X,若p的ε-邻域中至少包含δ个样本点,即若|Nε(p)⋂X|≥δ,则p是一个核心点。
定义3(边界点)对于任意样本点p∈X,若p的ε-邻域中包含小于δ个样本点,即若|Nε(p)⋂X|<δ,则p是一个边界点。
定义4(噪声点)噪声点是在其ε邻域内点的个数少于δ且邻域内的点均为边界点的点。
定义5(密度直达)如果p位于q的ε-邻域中,且q是核心点,则称p由q密度直达。
定义6(密度可达)如果存在一个样本点链p1,p2,…,pi,pi+1,…,pn满足p1=p和pn=q,pi是由pi+1关于ε和δ密度直达的,则点p是由点q关于ε和δ密度可达的。
定义7(密度相连)对于p和q,如果存在核心点h,使p和q均由h密度可达,则称p和q密度相连。
在DBSCAN中簇的定义是从一个核心点出发由密度可达关系导出的最大密度相连点的集合,即为最终聚类的一个簇。
1.2快速DBSCAN算法
将两组点集S1和S2之间的距离定义为d(S1,S2)=min{d(p,q)|p∈S1,q∈S2}。如果两个点集之间的距离大于ε,则两个点集中的点一定属于不同的类。传统DBSCAN算法中假设同一个核心点邻域内的点属于同一类。据此,本文对传统的DBSCAN算法进行了改进,提出了一种DBSCAN的改进算法——快速DBSCAN算法(FDBSCAN)。该算法以子类簇间交叠部分存在核心点为类簇合并依据,基于此扩展类簇完成聚类,避免了类簇扩展过程中邻域的冗余检索,从而加快聚类速度。具体算法步骤如下:
FDBSCAN算法步骤如下:
输入:数据集X={x1,x2,…,xn},半径参数ε,邻域密度阈值δ
输出:样本点类标签
步骤1根据给定超参数ε和δ,求出数据集X中的核心点,并将这些核心点按密度大小降序排序后存入集合S。
步骤2每次选择S中当前的第一个点p(即为当前密度最大的核心点),为p创建一个新的类簇C,然后将p从S中删除;对于p的ε邻域内已有类标号的点,将X中与该点类别相同的点全部标记类别C;将p的ε邻域内其余点的类标号记为C;将p的ε邻域内的核心点从S中删除。
步骤3将数据集X中剩余点聚类至邻域内最近的核心点所在类;邻域内无核心点的标记为噪声点。
2 融合网格划分与FDBSCAN的改进聚类算法(fusion of grid partition and FDBSCAN clustering algorithm,G_FDBSCAN)
2.1 改进的网格聚类算法
基于网格的聚类采用空间驱动的方法,把嵌入空间划分成独立于输入对象分布的单元[21]。该方法使用一种多分辨率的网格数据结构,将数据空间量化成有限数目的互不相交的网格单元,根据密度阈值将网格识别为高、低密度网格,将相连的高密度网格识别为簇。聚类质量取决于网格单元的划分粒度,如果划分粒度很细,则网格单元的数量会显著增加,从而使处理代价显著增加;如果划分粒度太粗,则属于不同类中的对象被划分到同一网格中概率会显著增加,从而降低聚类精度。这种方法具有线性的时间复杂度,对大规模数据集有很好的扩展性,但是,以网格取代数据点作为聚类基本单元,丢失了大部分点的信息,导致聚类质量下降。
有许多经典的基于网格的聚类算法。本文选择了基于网格和密度相结合的CLIQUE聚类算法。根据后面与DBSCAN算法融合的需要,对CLIQUE算法进行改进,提出一种改进的CLIQUE算法。下面根据两个超参数:网格宽度ε和密度阈值δ,给出网格聚类的一些相关定义。
定义8(网格单元)给定一个d维的数据集X,其属性(A1,A2,…,Ad)都是有界的,将d维数据空间的每一维划分成长度为ε的等长区间段,这样d个来自不同维度的区间段相交成一个(超)矩形,即为网格单元。
定义9(相邻网格)相邻网格是指有共同边的网格单元。
定义10(网格单元密度)网格单元u中数据点的个数称为该网格单元的密度,记作N(u)。
定义11(稠密网格)给定一个网格单元u,若N(u)≥δ,则u为稠密网格。
定义12(稀疏网格)给定一个网格单元u,若N(u)<δ,则u为稀疏网格。
改进的CLIQUE算法步骤如下:
输入:数据集X={x1,x2,…,xn},网格宽度ε,密度阈值δ
输出:样本点类标签
步骤1根据给定超参数ε和δ,将数据集X中的点映射到网格中,将所有网格划分为稠密网格和稀疏网格。
步骤2将相邻的稠密网格连接成簇;将稀疏网格中的点标记为噪声点。
2.2 G_FDBSCAN算法
通过结合网格划分方法,并改进原DBSCAN算法的执行步骤(FDBSCAN算法),提出了一种精确高效的聚类算法G_FDBSCAN算法。采用基于网格的聚类算法作为数据集分布度量,给出数据集密度分布特征,分而治之,从而在一定程度上避免DBSCAN采用全局参数引起的误差;仅对稀疏区域的点运用FDBSCAN聚类,将使用FDBSCAN聚类的对象数控制在平方的时间复杂度到达之前的数量级范围内,也可以在一定程度避免基于网格的聚类算法采用硬网格划分技术破坏聚类边缘造成的聚类精度差的问题。通过改进,在优化传统DBSCAN算法聚类结果的同时,大大降低了算法的时间复杂度。
采用网格划分技术将数据空间划分为多个网格单元,稠密网格所在区域称为密集区域,稀疏网格所在区域称为稀疏区域,分而治之。首先,对密集区域内的点进行预聚类,这些点位于类簇中心区域,通过合理调整用户参数,基本可以保证同一网格单元中的数据点属于同一类簇,数量大且易于识别。应用基于网格的聚类算法,可以快速、准确地获得初始聚类结果。稀疏区域中的点通常位于类簇的边缘区域,且其中可能存在噪声容易被误分类,数据量远少于密集区域,聚类难度较大。因此,针对稀疏区域的点,本文在现有网格划分的基础上,采用本文提出的FDBSCAN算法进行处理。
G_FDBSCAN算法步骤如下,流程图如图1所示。
输入:数据集X={x1,x2,…,xn},半径参数ε,邻域密度阈值δ
输出:样本点类标签
步骤1根据给定的半径参数ε和邻域密度阈值δ,利用网格划分技术将数据集划分为密集网格和稀疏网格。
步骤2对密集网格所在区域的点利用改进的CLIQUE算法进行预聚类。
步骤3将密集区域中网格聚类得到的每一个子类作为一个整体与网格聚类后剩余未聚类的点一起运用基于网格划分的FDBSCAN算法(确定核心点的邻域检索只在相邻网格范围内执行)进行聚类,同时识别噪声点,得到最终的聚类结果。
2.3 G_FDBSCAN的时间复杂度
该算法的时间复杂度为O(n)。假设n是数据集中点的数量,该算法的时间复杂度主要由两部分决定:(1)网格聚类,时间复杂度O(n)。此部分的时间复杂度由两部分组成:①划分数据空间,将每个数据点映射到网格单元中需要线性时间复杂度O(n);②筛选出高密度网格需要O(u),u是网格单元数,u≪n。(2)FDBSCAN聚类,即对网格聚类后剩余未聚类的点的聚类,时间复杂度O(ml)。此部分的时间复杂度由两部分组成:①计算核心点,邻域检索只在相邻网格范围内执行,时间复杂度为O(ml),m是网格聚类后剩余未聚类的点的总数,m≪n;l是近邻网格中的点数,l≪m。②扫描剩余的未聚类点就近归类,该部分的点数量很少,且基本都是位于类簇边界上,每个点就近归类时执行邻域检索所需扫描的点也很少,因此这部分的时间复杂度可以忽略不计。
综上所述,G_FDBSCAN算法的时间复杂度为O(n)+O(ml)=O(n)。
3 实验
3.1 实验数据集及设置
通过在人工数据集和真实数据集上进行对比实验来综合评估分析G_FDBSCAN算法的聚类效果和效率。人工数据集选取了5个不同形状、大小和密度的有一定结构复杂度的数据集(表1)。真实数据集选了7个不同大小、维度和类别数目的UCI(http://archive.ics.uci.edu/ml/datasets.php)数据集(表2)。对比算法包括BIRCH算法、KMEANS算法、DPC算法、CBSCAN算法[14]以及传统DBSCAN算法。
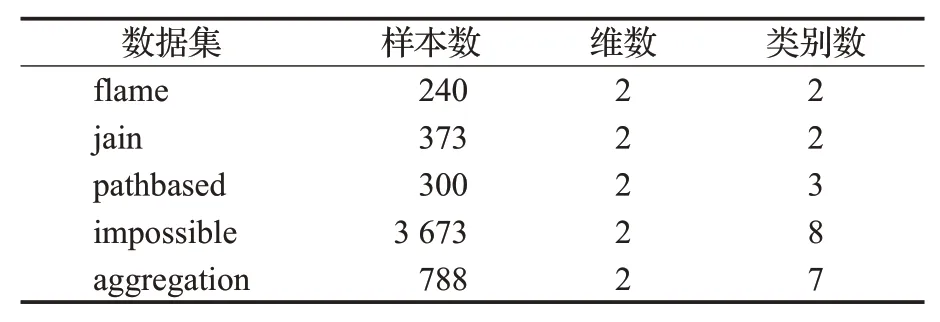
表1 人工数据集Table 1 Artificial datasets
本文通过两种常用的聚类评估指标对算法的性能进行评价:调整兰德系数[22(]adjusted Rand Index,ARI)和调整互信息[23(]adjusted mutual information,AMI),两种指标的取值范围为[-1,1],取值越大表示聚类结果和真实情况越吻合。实验基础环境为Intel®CoreTMi5-7500 CPU@3.40 GHz,8 GB内存,Windows10操作系统和anaconda3 Python。

表2 真实数据集Table 2 Real datasets
3.2 超参数对算法性能的影响
本节在impossible数据集和pendigits数据集上进行对比实验,运用控制变量法,分别将超参数ε和δ固定为最佳调整值,改变另一个参数的取值,来测试和评估这两个参数对新算法性能的影响。
每个超参数对算法评分的影响情况如图2。可以看出,ε和δ值的变化都会引起算法评分的波动,在两个数据集的最佳参数附近(impossible数据集:ε=1.0,δ=20;pendigits数据集:ε=42,δ=10),算法评分随ε值变化而产生的波动较大,随δ值变化而产生的波动较小。这是因为,ε的大小决定了每个数据点在网格划分中的区域定位,从而决定了数据对象在网格空间的整体布局,而δ的大小仅决定一个网格是否是高密度网格。因此,G_FDBSCAN算法评分对ε更为敏感。
图3展示了算法运行时间对两个超参数的敏感性。可以看出ε和δ都会影响算法的运行时间,但是运行时间对两个超参数的敏感性没有明显的偏向。原因是,G_FDBSCAN的运行时间主要受测试数据集中使用网格聚类的点的数量的影响。使用网格聚类的点越多,则使用FDBSCAN的点越少,时间效率就越高。因此,这一过程受到ε和δ的联合作用的影响。
3.3 复杂数据集中应用的鲁棒性
对表1所给出的人工数据集,使用5种聚类算法进行实验,这5个数据集的类簇分布情况和聚类的数目是截然不同的,它们可以更直观地反映出5种聚类算法的鲁棒性。聚类结果可视化描述如图4~图8所示,图中不同颜色(形状)的数据点代表不同类别。

图2 算法评分对ε/δ敏感性分析Fig.2 Sensitivity analysis of algorithm score toε/δ

图3 算法运行时间对ε/δ敏感性分析Fig.3 Sensitivity analysis of algorithm running time to ε/δ

图4 5种聚类算法对数据集flame的聚类结果Fig.4 Clustering results of five clustering algorithms on flame dataset

图5 5种聚类算法对数据集pathbased的聚类结果Fig.5 Clustering results of five clustering algorithms on pathbased dataset

图6 5种聚类算法对数据集aggregation的聚类结果Fig.6 Clustering results of five clustering algorithms on aggregation dataset

图7 5种聚类算法对数据集jain的聚类结果Fig.7 Clustering results of five clustering algorithms on jain dataset

图8 5种聚类算法对数据集impossible的聚类结果Fig.8 Clustering results of five clustering algorithms on impossible dataset
图4~图6是对3种密度均匀但类簇其他分布情况和聚类数目各不相同的非凸数据集聚类的结果。可以看出,KMEANS算法在3个数据集上的聚类效果都不理想;BIRCH仅在flame数据集上可以得到正确聚类数目而在pathbased和aggregation数据集上均出现了明显错误,将同一类簇中的点识别成了多个类;CBSCAN算法在flame和aggregation上聚类结果都很好,但在pathbased上聚类效果不佳;DBSCAN和G_FDBSCAN算法都可以正确划分数据类别。这表明KMEANS算法和BIRCH算法不能很好地对非凸数据集进行聚类。CBSCAN算法不能很好地聚类邻接的带环簇结构。同时,也可以看出G_FDBSCAN算法比DBSCAN算法对类簇边界点的识别更为精准。
图7是两个弧形且同一类簇内存在密度不均匀分布的数据集。从图中结果可以看出,BIRCH算法和KMEANS算法均存在将一个弧形簇的一部分划分到另一个类簇中的问题,CBSCAN算法和DBSCAN算法将存在密度不均匀分布的弧形簇划分成了两个类,G_FDBSCAN算法由于对数据集的不同密度区域采用分而治之的策略得到了正确聚类结果,聚类效果最好。
图8是类簇形状和密度分布情况复杂的数据集。在图8的聚类结果图中,G_FDBSCAN算法和CBSCAN算法均得到了正确的聚类结果,其他三种算法均有一定偏差。BIRCH算法和KMEANS算法聚类效果都很差,将同一类簇识别成多个类,DBSCAN算法在类簇边缘处的识别效果不佳,这主要是由于其使用全局参数所致。
聚类结果量化描述如表3所示。从表3可以看出,在ARI和AMI指标值方面,BIRCH算法和KMEANS算法在5个数据集上的指标值大多在0.5或0.5以下,且在不同数据集上波动较大;G_FDBSCAN算法、CBSCAN算法和DBSCAN算法在不同数据集上的指标值都接近于1,算法性能稳定,且G_FDBSCAN算法在各种复杂数据集上的鲁棒性最强,在所有测试数据集都是最优值或非常接近最优值。在时间性能方面,G_FDBSCAN算法所需时间最短,CBSCAN算法次之,BIRCH和KMEANS算法时间开销也较小但在一些数据集上有波动,DBSCAN算法所需时间最久且和其他3种算法所需时间明显不在同一量级,这在数量较大的aggregation和impossible数据集上尤为明显。
综合分析可知,G_FDBSCAN算法的综合性能最佳,不仅聚类速度快,而且对于各种分布复杂的数据集具有最强的鲁棒性。
3.4(超参数)最佳调整下的性能
本节在7个UCI数据集上测试,因为CBSCAN算法不支持高维数据,所以选择增加和DPC算法的对比实验,参数最优化调整下各算法的聚类结果如表4所示。为减少实验误差,每个数据集独立运行10次,取平均值作为最终实验结果。通过实验结果可以看出,在参数最优调整下,G_FDBSCAN算法的ARI和AMI指标值和运行时间均是最优值或接近最优值,且在不同数据集上性能稳定;DPC算法和DBSCAN算法聚类效果较好但算法时间开销很大,在pendigits这样的大规模数据集上对比更加明显;BIRCH算法和KMEANS算法聚类速度较快,但在不同数据集上聚类结果差异大,在wine数据集上ARI和AMI指标值和G_FDBSCAN算法相差接近100倍。这表明,G_FDBSCAN算法能较好地平衡算法的聚类效果和时间开销,算法性能优越,实际应用中能更好地扩展到各种复杂的大规模数据集。
4 结束语
G_FDBSCAN算法是一种快速聚类算法,该算法通过将密度聚类算法与网格聚类算法融合,以及改进DBSCAN算法执行过程(FDBSCAN算法),两方面降低DBSCAN算法的时间复杂度,同时降低了使用全局参数对算法性能的折损,优化聚类结果。本文通过理论和实验分析,证明G_FDBSCAN算法可以在一定程度上减少计算量,获得与BIRCH、KMEANS、CBSCAN这些快速算法同一量级甚至更快的聚类速度,以及比DPC算法和DBSCAN算法更优的聚类结果,从而在大规模数据上获得较好的可扩展性。此外,改进后的算法聚类结果稳定、鲁棒性强,可以在类簇大小、形状和密度不同的复杂数据集上获得较好的聚类结果。本文还通过实验分析了算法对不同超参数的敏感性,得出的结论可以指导算法实际应用中的参数调整。

表3 5种聚类算法在人工数据集上的性能对比Table3 Performance comparison of five clustering algorithms on artificial datasets
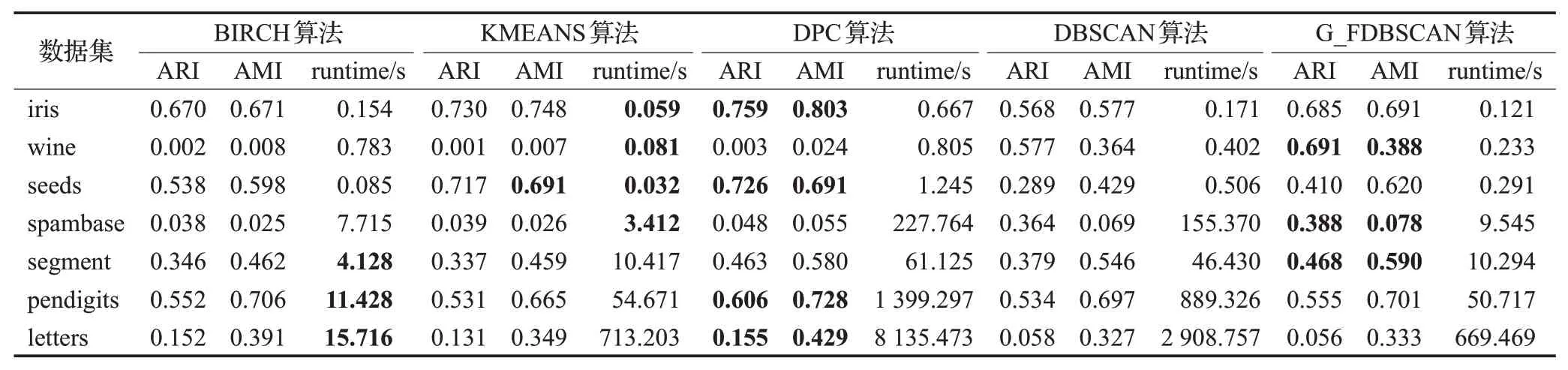
表4 5种聚类算法在真实数据集上的性能对比Table 4 Performance comparison of five clustering algorithms on real datasets
