相约两世纪之网络画板与丹德林双球模型——圆锥曲线证明的直观方法

●付小华，幸世强，代月，张红

笔者在一次四川省国家级“双新”示范区(校)建设推进会，成都市第七中学第43届教育研讨会的研究课“穿越两世纪的魅力内切球”中，通过网络画板深度探究丹德林双球模型在证明圆锥曲线时的一些做法和思考，多种直观证明非常巧妙，极具创造性，网络画板动态立体几何深度融入数学教学，让数学课堂充满智慧的魅力。

一、网络画板辅助构造丹德林双球模型

一个圆锥被一个平面斜截的截口曲线将分别出现椭圆、抛物线和双曲线的一支。要构造丹德林双球模型，可以引导学生思考问题1：一个圆锥被一个平面斜截，与圆锥和斜截面都相切的球怎么构造？球心在哪？半径怎么构造？其设计意图是：让学生经历找球心、构半径的过程，对这种丹德林内切球的空间结构、空间位置关系、几何性质更加熟悉，为后面直观探究丹德林双球模型证明圆锥曲线打下坚实的基础。

①作底面半径为a，高为b的圆锥，在圆锥高SO上任取一点C，过C做SO的垂面α，将垂面旋转角 t，设置变量 t∈（-π，π）（图 1）。

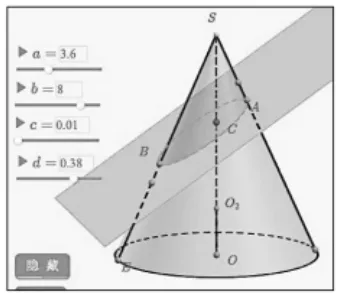
图1

②过S作旋转面的垂线，垂足为D，连接CD交圆锥于A，B，作母线SA与 SB（图 2）。

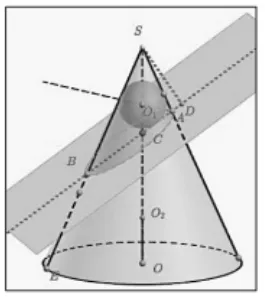
图2

③做∠SAC与∠ABE的角平分线分别交锥高SO于O1、O2，即为内切球的球心,做O1到SA和O2到SB的距离,即为内切球的半径,进而作出双内切球（图 3）。

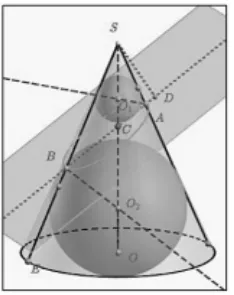
图3

二、网络画板赋能丹德林双球模型证明圆锥曲线

继续引导学生思考问题2：这种与圆锥和斜截面同时相切的双内切球有什么性质特点？如何证明圆锥曲线呢？其立体几何构图和深层次思维在哪里呢？

继续提供和推送网络画板课件资源进行观察探究、想象思考和推理证明，然后在此次基础上进行生生、师生对话分享、展示交流、引导讲解。

（一）丹德林是怎么证明椭圆的

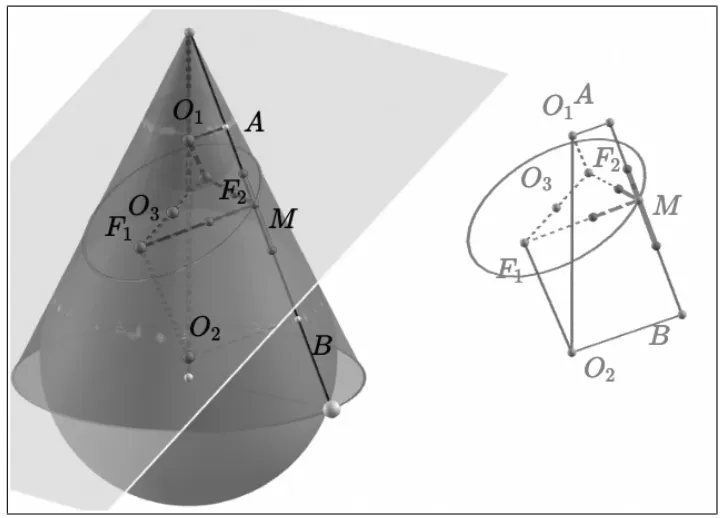
图4

由球和圆的几何性质，因为MF1=MB，MF2=MA，所以MF1+MF2=MB+MA=AB。

所以，A，B随着点M的运动而运动，但是AB长度为定值，即截面曲线上的任意一点M到两个定点F1，F2的距离之和是定值（且大于F1F2），由椭圆的定义可知，该曲线为椭圆。

所以，当β＞α时，截面曲线为椭圆。

（二）沿着数学家的探究脚步，怎么证明双曲线

由球和圆的几何性质，因为MF1=MB，MF2=MA，所以｜MF1-MF2｜=｜MB-MA｜=AB。

所以，A，B随着点M的运动而运动，但是AB长度为定值，即截面曲线上的任意一点M到两个定点F1，F2的距离之差的绝对值是定值 （且小于F1F2），由双曲线的定义可知，该曲线为双曲线。所以，当0°≤β＜α，且截面不过O点时，截面曲线为双曲线（图5）。

图5

（三）丹德林双球模型能证明截口曲线是抛物线吗

丹德林双球模型证明椭圆与双曲线中，我们可以发现双球与平面相切的切点是椭圆或双曲线的焦点，同时通过到这两个定点的距离之和与差的构造，转化为球外一点到球的切线长相等，进而进行计算、得证。但是抛物线没有这样的特点，这种思路明显受阻，怎么办？怎么证明？

（四）探究丹德林双球模型与圆锥曲线离心率关系并证明

再引导学生思考问题3：平面斜截圆锥时锥角与平面倾斜角不同，得到的圆锥曲线不同，与离心率有怎样的关系？运用丹德林双内切球模型，可不可以用离心率统一定义证明圆锥曲线？准线可能在哪？

由题知，圆锥的锥角的一半为α，斜截面与圆锥轴所成角为β。

因为O2F1∥O1F2，所以在面O2F1O1F2中作O2D∥O1F2，O1D∥F1F2交 D。

因为O2B∥O1A，所以在面O2BAO1中作O1C∥AB交O2B于C。

说明只需利用丹德林双球模型中的两个关键角的余弦值之比即为截口曲线的离心率，进而由离心率e的范围就可以判断和证明出圆锥曲线是椭圆、双曲线还是抛物线，十分简洁明了，我们把此模型叫做锥角倾斜角模型（图6）。

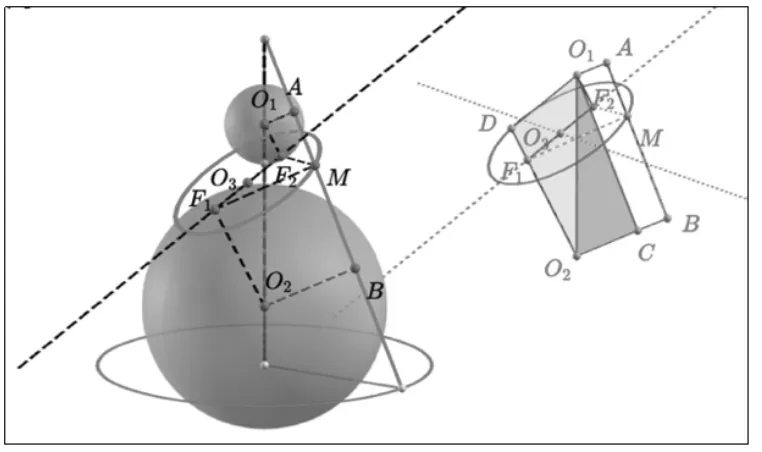
图6

（五）丹德林单球模型圆满证明圆锥曲线

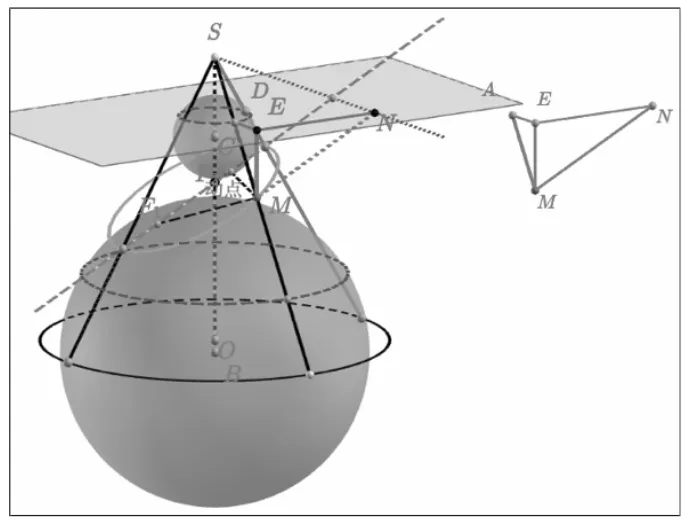
图7

我们把这种构造和证明叫做圆锥曲线第二定义模型，这种思路将圆锥曲线的第二定义与锥角倾斜角模型融会贯通，非常巧妙，一气呵成。

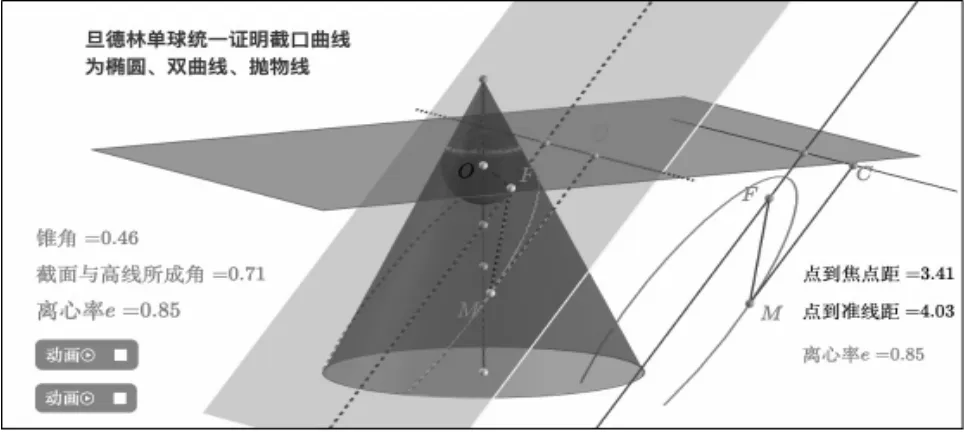
图8

本节课“穿越两世纪的魅力内切球”网络画板课件网址：https://www.netpad.net.cn/presentationEditor/presentationPlay.html#posts/15307

三、网络画板赋能丹德林双球模型证明圆锥曲线的价值

丹德林双球模型和内切球的性质特点证明圆锥被平面所截的截口曲线是三大圆锥曲线——椭圆、抛物线和双曲线，这个问题深奥、难懂，特别是用锥角模型和第二定义模型证明圆锥曲线难度更大，需要充分利用网络画板3D技术辅助识图、构图、思考、探究、推理、计算、证明。

张景中院士一直主张数学教育就是要 “把数学变得容易”“让数学更有趣”“让数学更精彩”“在玩中学，在做中学”[1]，通过网络画板实现了这些要求。