把握数学概念本质,发展数学核心素养
2022-07-20崔永红
●崔永红
《普通高中数学课程标准》(2017年版2020年修订)指出:“数学教学以发展学生数学学科核心素养为导向,创设合适的教学情境,启发学生思考,引导学生把握数学内容的本质。”为此,在数学概念教学中,可以通过信息技术演示、适时问题引领,让学生经历概念的抽象过程,从而把握概念的本质,提升学生直观想象、数学抽象、数学建模、逻辑推理等核心素养。
一、通过信息技术与逻辑推理,把握概念的本质
不少数学概念有其发生、发展的历程,教师要挖掘概念背后深邃的数学思想、方法与文化,揭示概念产生的合理性和必然性,让学生不仅知其然,而且知其所以然,这样学生学习的积极性就越来越高,数学核心素养得到有效提升。
案例1 椭圆的概念
在进行椭圆的概念教学时,让学生用一根细绳和画板动手操作,画出椭圆,然后引导学生观察抽象得出椭圆的概念,但在教学中,学生总有这样的疑问:为什么这样画出的图形是椭圆?怎么想到的?怎么发现椭圆的特征呢?
为了解决学生的疑问,教师利用信息技术动态演示,问题引领,师生合作,取得了较好的效果。
信息技术演示:用一个平面(与圆锥的旋转轴不垂直)将圆锥切开,如图1所示。

图1
师:其截面,如图2所示,这是什么图形呢?

图2
生:椭圆。
师:很好!确实是椭圆。
这一问,让学生产生了认知冲突。这时教师乘势而上,再利用信息技术演示,引导学生观察、分析、交流与讨论。
信息技术演示:在截面的两侧分别放置一个球,使它们都与截面相切,切点为F1、F2,且与圆锥面相切,两球与圆锥面的公共点分别构成圆O1和圆O2,如图3和4所示。

图3

图4
设点M是平面与圆锥面的截线上任一点,过M作圆锥面的一条母线分别交圆O1,圆O2于P,Q两点,如图5。
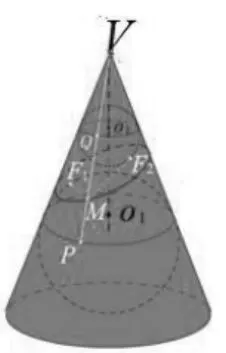
图5

图6
师:在图5中,你能得出哪些结论?
学生一时无从回答,在学生的探究无法深入的时候,教师提示。
师:图5中有哪些线段相等?
这时有学生小声讨论,发现了相等的线段。
这个问题真是“雪中送炭”,起到导向、引领的作用,帮助学生找到研究“椭圆”的方向和突破口。
生 1:MP=MF1,MQ=MF2
师:为什么?
生2:因为 MP和 MF1,MQ和MF2分别是上下两球的切线,因为过球外一点所作球的切线的长都相等,所以 MP=MF1,MQ=MF2
师:将上面两式相加,得到
MF1+MF2=MQ+MP=PQ
师:线段PQ的长有何特点?
学生一边观察,不时交流与讨论,教师与学生为伍,一边指导,一边点拨。
生 3:因为 PQ=VP-VQ,而 VP,VQ 分别是两个圆锥的母线的长,是常数,所以线段PQ的长也是常数。
师:即截线上任意一点到两个定点F1,F2的距离的和等于常数。这就是椭圆的本质特征。至此,你能给椭圆下一个定义吗?(略)
为进一步让学生加深对定义的理解,教师又提出了下面两个问题:
追问1:已知△ABC的周长为20,一条边BC的长为6,则顶点A的轨迹是什么?
追问2:你能用一根长为20厘米的细线在平板上画一个椭圆吗?
教学感悟:在教学中运用信息技术演示用平面将圆锥切开的过程,得到椭圆面,学生自然产生认知冲突:椭圆是怎么定义的?在学生无助时再用信息技术演示,迫使他们深入思考下去,迫使他们认真思考“椭圆”的特征,迫使他们观察、交流、讨论与反思,椭圆概念的产生成为水到渠成、浑然天成的产物,这个概念不是“人造”而是“神造”的。在此基础上,再通过追问1和2进一步引导学生思考,在做中体悟椭圆的本质,加深对椭圆的认识。
二、通过问题引领与数学建模,把握概念的本质
在概念教学中,可以通过设置问题串,引导学生思考与交流,建立数学模型,从而把握概念的本质内涵。
案例2 导数的概念
某市6月2日7时至14时气温变化如图7所示,你会有什么感叹?

图7
生1:12时到14时会让人感到有些闷热。
师:从A时到B时气温变化为15.1,从B时到C时气温变化为14.8。气温变化差不多,使人感到闷热是什么原因呢?
生2:天气热得太快了!前者变化得缓慢,而后者变化得太快。
师:比较气温变化的快与慢,只考虑yC-yB行不行?如不行,还必须考察什么量?
生3:还必须考察xC-xB。
师:那如何比较气温变化的快慢?
生4:可以用单位时间内平均气温来比较。

师:对于上述问题,我们怎样求x=12时的气温呢?
到此,我们就建立了一个数学模型,用瞬时变化率量化变量在某一点处的变化快慢。导数的概念水到渠成,导数的本质就是瞬时变化率。
教学感悟:教学中通过实例由浅入深、由表及里,经历由平均变化率过渡到瞬时变化率的过程,直观认识平均变化率与导数的区别与联系,体会变化率的实际背景。通过问题引领,层层揭示建构数学模型的思维过程和数学知识的内在联系。
三、通过类比归纳与直观想象,把握概念的本质
类比能启迪人们的思维,是数学发现、发明的主要源泉,但类比是一种主观的不充分的似真推理,因此,要确认其猜想的正确性,还须经过严格的逻辑论证。
案例3 异面直线所成角的概念
师:如图8,蜗杆与蜗杆的轴线a和b是什么位置关系?
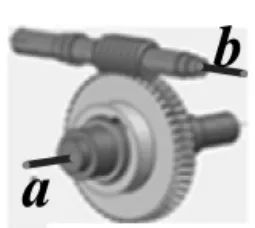
图8
生1:轴线a和b始终是异面直线。
师:如图9,a与b、a与l是异面直线,是否还有什么不同呢?
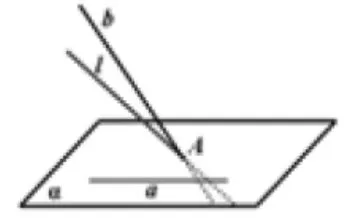
图9
生2:好像b、l相对于a的“倾斜程度”不同。
师:如图10,平面内直线b、c与直线a相交,我们怎样刻画直线b、c相对于直线a的倾斜的程度呢?
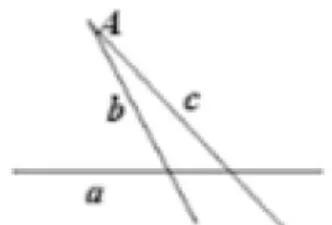
图10
生3:可以过A点作直线c,使c//a,可以用相交直线b与c所成角来表示直线b相对于直线a的倾斜程度。
师:这样表示,所成的角是唯一确定的吗?为什么?
生4:唯一确定,因为过A点作直线a的平行线是唯一的。
师:由于是唯一确定的,因此可以用相交直线b与c所成角来表示直线b相对于直线a的倾斜程度。
生5:过直线b上任一点作直线a的平行线都可以。
师:还有更一般的作法吗?
生6:可以过空间任意一点分别作直线a,b的平行线c,d,用c和d所成角来表示a,b所成角。
师:我们采用的方法是将空间问题转化为平面问题,转化的关键是平移,这种方法在今后的学习中还有很多应用。
于是,学生在老师的指导下,通过类比、合作、探究、归纳发现了异面直线所成角的概念。
教学中始终将数学抽象贯穿于概念产生、发展、应用的过程中,自然生成了异面直线所成角的概念,促进学生养成在生产生活中思考问题的习惯,发展了学生数学抽象的素养[4]。
总之,在遵循认知心理学关于概念获得的相关理论的前提下,要以概念形成方式进行教学设计,让学生经历观察与实验、分析与综合、归纳与概括,感悟概念的产生过程,让数学抽象、直观想象、数学建模等核心素养在潜移默化中得到提升。
