整体教学视域下数学习题统整策略探寻
2022-07-20王灵勇
●王灵勇
2017~2019年,笔者协助江山市教研室对我市200位小学数学教师进行了抽样调查,发现教师很少从“整体教学”理念出发精心设计习题。基于区域课堂教学存在的问题,为切实提高区域教师整体把握教学目标、整体解读教材、整体研究课例、整体设计习题等能力,本文就“整体设计习题”这一主题谈谈自己的实践经验。
一、一题多问,在核心问题的引领下培养探究精神
核心问题是基于教学中的核心知识和学生认知水平,关注数学核心素养,引领学生开展探究学习的数学问题。教学过程中,教师要创设激活学生思维的数学问题,为学生的探究学习提供空间,促进深层次的学习。
(一)基础题学生自主提问,拓宽思维广度
培育学生的数学核心素养,要追求有深度和广度的教学,推动学生思维递进,拓宽学生思维广度。基础题“一题多问”,解决多元化的数学问题,是拓宽学生思维广度强有力的举措之一。
以分数乘除法教学为例,如何能找准单位“1”,这是解决分数乘除法相关问题的关键。教师在课堂练习中可以利用一题多问,强化学生对单位“1”的理解。
例如,学校开展德育币兑换奖品活动,王华有60枚德育币,王琴有40枚德育币,?教师启发学生思考:依据这一组信息,你可以提出哪些用分数乘除法来解决的数学问题呢?放手让学生尝试,学生提出并解决以下六个问题:
通过以上“一题多问”的教学过程,让学生进一步巩固找“单位1”的方法,发现解决这一类型的问题都是由“单位1”作为除数。
(二)常规题一题多问,深入挖掘出亮点
对常规习题进行一题多问,通过分层递进的问题,把看似平常的一些练习题进行深入挖掘,成为题组搭配、一题多练、分层提高的练习,让教学亮点纷呈。比如三角形三边关系中有这样一道题:
哪几组小棒能搭成三角形?在能搭成三角形的后面画“√”。
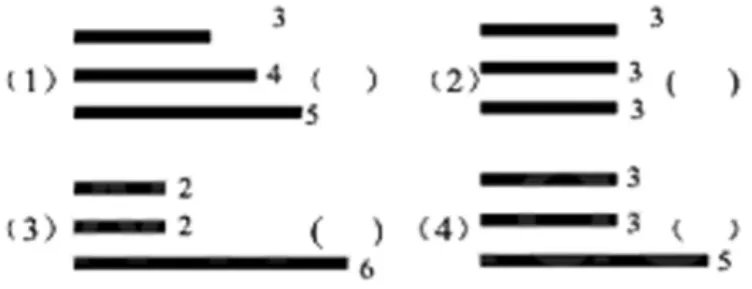
图1
这是一道很常规的练习题,学生可以直接运用“三角形较短两边之和大于第三边”,对学生来说并不难。但我们可以通过分层递进的问题进一步挖掘:
1.为什么(3)不能围成三角形,而(1)(2)(4)能?
2.像3、4、5这样三个连续自然数的三条边围成的是什么三角形?是不是所有三个连续自然数的三条边都能围成三角形?
3.你能想办法使(3)能围成三角形吗?你有哪些方法?
4.(4)中如果调换“5”这根小棒,能换成哪些长度?你发现了什么?
以上四个问题分层递进,让教学亮点纷呈,为探究三角形的特征提供了很大空间,学生的推理能力、想象能力、数感、空间观念得到了很好的发展。
(三)思维题教师预设“问题串”,引导深入探究
怎样更好引领学生进行探究性学习呢?笔者首先进行的实践是:针对每一道思维题,教学中精心预设问题串,用一个个激活学生思维的问题引导学生深入探究。下面以北师版四上“探索与发现(1)”中的“999999×999999=?”一题为例设计问题串。

图2
问题1:看第二关:999999×999999=?怎么算?(生疑惑)
问题2:计算器也帮不了我们了,可否从“111111×111111”中得到一些启示呢?
问题3:先算一算,接下来你有什么好建议吗?
问题4:仔细观察、思考,对积和乘数之间的关系有什么发现?
问题5:再挑战你一题,99999980000001这是几乘几?怎么想的?
问题 6:99999999×99999999,积是几位数?
问题7:我出一道题考考你们,如果是八个三乘八个三,怎么算?
……
以上一道思维题,教师通过问题串,启发学生不断思考探索,经历思维发生发展的过程,体验再创造的快乐:①基于学科本质,学生真正感到有疑问。②教师的问题统领了整个思维过程。③在教师问题的引领下,学生提出了变式问题,实现了再创造。
二、一题多变,在沟通联系中实现数学的融会贯通
一题多变可以克服认知偏差,提升思维广度,训练思维灵活性,它有利于培养学生的数学思维和创新意识[2]。
(一)进行题组对比,理解关系,提升解题方法
根据笔者的教学经验,一题多变的方法,在训练数量关系变式、强化解题方法使用方面能取得比较好的教学效果。改变题目的条件和问题,通过相似或不同材料的对比、分析和思辨,形成正确的思考方式、解题技巧。以“分数乘除法”为例,合理地改变条件和问题,教学效果显著。
学习了“分数乘法”后,学生整体掌握情况都不错。但在学习“分数除法”之后,情况却非常糟糕,遇到实际问题学生往往眉毛胡子一把抓,分不清乘和除。教学中可以通过设计变式题,帮助学生理解数量关系,把握解题方法。
1.信息与问题互相转换,理清数量关系
出示以下三组题:
(1)王华有60枚德育币,王琴有40枚德育币,王琴的德育币是王华的几分之几?
以上三道变式题,能帮助学生整体理解标准量(单位“1”)、比较量(对应量)、对应分率之间的数量关系,解决复杂的分数应用题。
2.体会单位1作为已知和未知不同的解法
掌握了基本数量关系和方法,学生在解决分数乘除法实际问题时还是会出现找单位“1”、分析数量关系存在困难,以及不能灵活应用的情况。教师要重视出类似以下的变式题,逐步提高学生的实际解题能力。
(1)学校组织的德育币兑换奖品活动中,亮亮有80枚德育币,明明的德育币比亮亮少了,明明有多少枚德育币?
(2)学校组织的德育币兑换奖品活动中,明明有80枚德育币,明明的德育币比亮亮少了,亮亮有多少枚德育币?
学生通过两题的对比交流,不难发现,两题中单位“1”的量都是亮亮的德育币数量,第(1)题单位1已知,求明明的德育币用乘法计算;而第(2)题亮亮的德育币数量未知,用除法计算。本组练习结束之后,再让学生创编一组类似的题目来练习。
(二)进行分层变式练习,训练思维灵活性
分层变式练习,有助于巩固基础,促进提升,实现学生差异性发展;有助于沟通知识间的联系,让思维融会贯通;有助于提高学生的数学综合能力、数学迁移能力;有助于训练学生的思维灵活性,提高思维品质。
比如,在复习分数乘除法的时候,根据“图书馆有2400本故事书,借出,借出了多少本”这一情境,设计如下的开放分层变式训练:
(3)图书馆有一批故事书,第一次借出300本,第二次借出500本,还剩下。一共有多少本故事书?
……
这种分层变式练习,思维多元,解决问题的策略更多样;思维灵活,思考问题角度更具创新;思维深刻,思考问题更有深度。
三、一题多悟,在质疑思辨中培养理性精神
教学中常常发现这种现象,一道题即使反复讲解和练习,仍有很多学生出错,对核心内容理解不到位,解题策略没形成。数学教学应注重一题多悟,达到“解一题,学一法,会一类”,感悟解题策略,培养理性精神。
(一)注重“素材重组”,悟透“疑惑”,明晰“本质”
当大部分学生解题方法出现混乱和疑惑时,我们需要追本溯源,重组素材,悟出本质,以求促进学生的发展。
学习了“分数的意义”和“分数与除法的关系”后,对于下面的题目:把3米长的彩带平均分成5段,每段长( )米,每段占全长的( )。笔者对班级情况做了一些摸底,答题情况如表1所示。
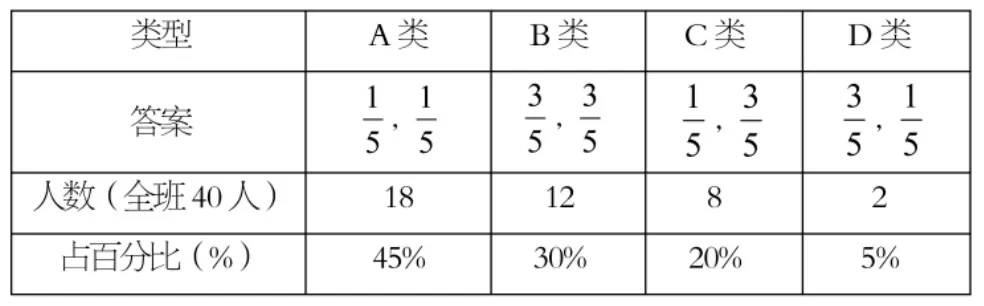
表1
教师整体呈现以上四种情况,引导学生讨论:(1)在小组当中说说自己这样填的理由。(2)对其他同学的方法你是怎么想的?(3)正确的是怎么样的?想办法把道理说清楚。
通过对A类、B类这两组同学做法的交流感悟,发现很多学生从刚开始不知道“有单位”“无单位”有区别,到发现有区别。但在讨论和说理过程时也说不清楚两者有什么本质的区别:什么时候应把一些物体看成单位“1”,什么时候应该考虑具体的数量。
接着教师追问:你们的两个( )的答案为什么不一样?(指C、D类同学)
通过C类、D类两组同学的交流感悟,孩子们的思路逐渐清晰,题目中两个( )要解决的问题不一样,一个是每段长多少米,一个是每段占全长的几分之几。第一个问题,可根据“总数÷段数=每段数”来填,比如改成5米长的彩带平均分成5段,每段就是 5÷5=1(米),以此类推,3 米长就是,而第二个问题是把全长看成单位“1”,把单位“1”平均分成5段,每段占全长的,和多少米长度无关。
学生经过激烈的思辨和充分的感悟,教师变换不同的长度,配合图进行解释,学生感悟到用“总数÷段数=每段数”理解米的道理,感悟到根据分数的意义理解了这个不变的道理。学生通过一题多悟疑惑点,理清了概念和计算的不同。
(二)注重回顾反思,悟透“脉络”,领悟“思想”
教师要根据不同的习题、不同的学段,教学中有针对性地引导学生进行回顾反思。教学对中低段要注重让学生初步形成回顾与反思意识,培养学生“一题多悟”的意识,重视对结果合理性的判断。一道题解决完后多问:你的解答正确吗?应该怎么检验?对中段年级学生注重培养回顾自己思考过程的习惯,能对结果的实际意义作出解释。平时教学中学生解完一道题以后多问:回顾你的解题过程,你有什么体会?对高段年级,在引导学生回顾的基础上,学会分析自己思维结果的合理性、思维过程的得与失,并总结经验,提炼数学思想方法,积累解决问题的策略经验、应用经验。教学中学生解完一道题后可以多问一些:解决这道题的关键是什么?你成功或失败的原因在哪里?它还可以解决哪类问题?
平时教学中教师要做到心中有数,教会学生灵活选择方法,做好回顾反思。如果是学生以前接触的旧题型,之前已经形成解题策略,那么就只对结果进行检验;如果是新题型,就有必要反思回顾过程形成策略,沟通与旧知的联系,领悟数学思想,再检验结果。
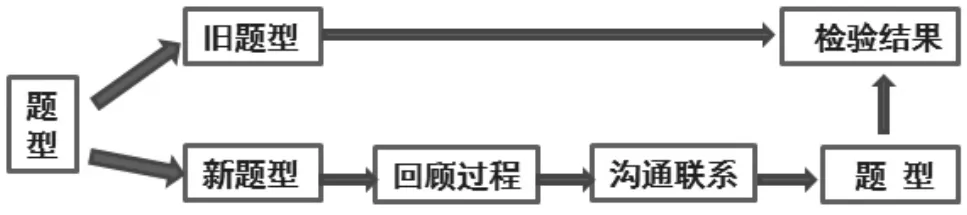
图3
总之,数学教育者应该重视“整体教学”视域下数学习题的研究,以“一题统整”的方式进行教学,如此,相信学生的数学核心素养定能得到实实在在的培育。
