时间测度链上四点边值问题正解的存在性
2022-07-20魏嘉王静
魏嘉, 王静
(兰州文理学院教育学院, 甘肃兰州,730000)
1990 年Hilger[1]首次提出了时间测度链相关理论。时间测度链理论将连续分析理论和离散分析理论进行了完美统一, 不仅避免了连续分析和离散分析的重复研究, 而且可以系统地洞察微分方程和差分方程之间的关系, 这对发展分析理论研究具有重要意义。而后人们利用时间测度链相关理论解决了诸多原来微分方程、差分方程无法单独解决的应用性问题, 如Thomas 等用时间测度链上的动力方程弥合了西尼罗河病毒传播的连续与离散之间的空隙等[2]。近20 年来, 时间测度链上的动力方程边值问题的研究引起了学术界的高度关注和广泛兴趣[3-12]。文献[13]利用上下解方法研究了方程uΔ4(t)=f(t,u(σ(t))·uΔ2(t)),t∈[ 0,1]在条件u(0) =0,u(σ4(1)) =0,auΔ2(η)-byΔ3(η) =0,cyΔ2(ξ)+dyΔ3(ξ) = 0下正解存在性。
受此启发, 本文研究时间测度链上四阶四点边值问题

的正解存在性。其中,T表示时间测度链,σ(t)是T上的向前跳跃算子,t∈[0,1]⊂T,0≤η<ξ≤σ(1)。
1 预备知识
为了讨论边值问题(1)正解的存在性, 先介绍如下定义。
定义1测度链是指实数集R 的任意一个非空闭子集, 通常记为T。
定义2对于t∈T, 定义向前跳跃算子σ:T→T为σ(t):= inf{s∈T:s>t},定义向后跳跃算子为ρ(t):= sup{s∈T:s<t}。
假设:(H1)a,b,c,d≥0,λ≥σ3(1)-σ2(1);(H2)q(t) ≥ 0。若q(t) ≡ 0,则a+c> 0;(H3)k=ad+bc+ac(ξ-η)>0,b-aη≥0,d-c(σ(1)-ξ) ≥ 0。
首先考虑线性边值问题
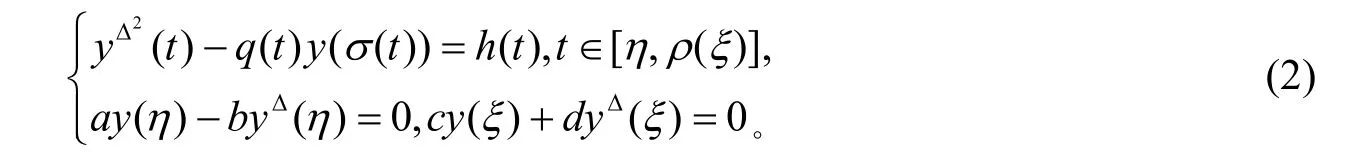
设φ和ψ是式(2)中所对应的齐次方程

在初始条件

的解。设

由式(3)和(4)可得

下面给出几个重要引理。
引理1若(H1)和(H2)成立, 则有φ(t) ≥ 0,t∈[η,σ(ξ)];ψ(t) ≥ 0,t∈[η,ξ];φΔ(t) ≥ 0,t∈[η,ξ];ψΔ(t) ≤ 0,t∈[η,ξ]。
证明由条件(H1)和(H2), 易证结果。
引理2若(H1)和(H2)成立, 则D>0。其中D如式(5)所示。

若q(t) ≡ 0, 则式(8)成立。再由(H2), 可得D> 0。
引理3设(H1)和(H2)成立, 若h∈C[η,ρ(ξ)], 则边值问题(2)有唯一解

其中
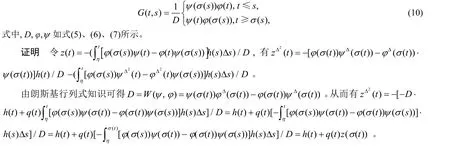

式中,D,φ,ψ如式(5)、(6)、(7)所示。

2 主要结果


证明考虑边值问题,

