基于病毒侵染和逆转操作的改进遗传算法
2022-07-20刘艳琪刘一杰
刘艳琪, 刘一杰
(南华大学数理学院, 湖南衡阳,421001)
能用多项式时间算法计算得到结果的问题称为多项式问题, 也就是P 问题[1]。能用多项式时间算法检验解的正确性但不可以用多项式时间算法求解的问题叫做NP 问题。研究NP 问题是否可以转换为P问题的这一类问题就是NPC 问题, 也被称为NPC 完全问题。
作为典型的NPC 问题,TSP 优化问题[2]等价于一个人一次性无来回遍历N个地点最后回到起点的最短路径问题。通过穷举法求解该问题的时间复杂度随着问题的规模呈指数增长, 而蚁群算法、模拟退火算法和遗传算法等启发式的智能算法[3]可以较快时间地得到该类问题近似最优解。意大利学者Marco Dorigo 在研究蚂蚁觅食的过程中提出了蚁群算法[4]。在蚁群中, 虽然单个的蚂蚁行为简单, 但其种群的整体却表现出了智慧性。蚂蚁们在搜寻食物的时候会释放信息素, 信息素浓度随时间递减, 蚂蚁们会偏向选择信息素浓度较高的路径行走并释放新的信息素, 从而达到正反馈调节得以寻找优化路径。Dorigo等人模仿该原理, 在待优化的问题上随机生成初始解以构成初始解空间, 再通过编写信息素产生函数来模拟蚂蚁产生信息素, 并在有限个解空间中进行迭代以模仿蚁群行为得到问题的较优解[5], 但是这类算法搜索速度较慢, 搜寻时间长, 并且当没有“蚂蚁”去寻找新的路径时, 信息素会被主流路径统治, 从而使算法陷入局部最优解。模拟退火算法是在N.Metropolis 研究“固体在加热后粒子会逐渐呈无序态而温度下降时固体内部粒子逐渐呈有序态”之后提出[6], 算法的基本思想为: 研究待优化问题设置初始解,若该解不“好”则通过“加热函数”使得该解跳到其邻域内并且逐渐冷却(即收敛到该邻域的极值点), 如此循环直到解符合优化后的条件才算评估完成。该算法具有渐进收敛性, 而且可以达到全局并行收敛, 具有较强的鲁棒性。但其加热函数和冷却函数等函数的参数不好调节, 如冷却太快的话可能较快得到最优解, 也可能直接跳过最优解。美国John holland 提出的遗传算法基于遗传学进行进化的模式, 对复杂问题进行简单编码、选择、进化的步骤来产生问题的自适应解[7]。同样作为启发式算法, 遗传算法依据简单的自然选择优胜劣汰学说, 将生物学的基本原理融合运用到了搜索进化过程, 使其具有广泛的适用性。它将自然界适者生存理论作为进化的基础, 结合随机交换的思想, 提高了搜索速度所以可以在短时间内获得复杂问题的较优解。在此之上,Holland 还提出了加入逆转操作的遗传算法。这种融合算法[8]在进行染色体编码、交叉互换和自然选择等操作时的基本原理与传统算法相同, 其不同点是额外加入了逆转操作[9]。编码后的染色体在遗传过程中通过依概率进行生物学中的“染色体倒位”操作, 使染色体更具有多样性。不仅如此, 倒位后的染色体也会进行自然选择从而保证染色体的质量进而使得该算法更容易跳出局部最优解。二十世纪九十年代,Kubota 加入病毒种群感染[10]的形式对遗传算法进行优化研究,基本原理是: 种群在每一次自然选择后, 病毒种群都会去复制较优秀的个体染色体来实现“寄生”, 相当于每次都选出本代优秀个体使得它们的存活率增加, 这样可以显著加快其收敛速度但是也同样使算法容易陷入局部最优解[11]。
通过分析不同算法的原理及各算法在对应条件下的优缺点, 从而对各种算法进行融合应用使得原算法得到改进。这是提升算法性能的有效方法。本文在遗传算法的基础上加入病毒侵染操作和染色体逆转操作以优化遗传算法。在宏观上继承传统遗传算法框架, 依旧完成种群的编码、初始化、交叉变异、自然选择、繁衍等过程, 从微观来看加入病毒种群来侵染每一代种群以加快收敛速率。侵染后的种群在染色体交叉互换和变异后采用逆转录的思想提高种群多样性(即解的多样性), 以此来加快该算法的收敛速度并使优化遗传算法难以陷入局部最优解。
1 TSP 问题描述
本TSP问题的具体描述为: 一个推销员需要去若干个城市推销, 每个城市只可以去一次, 那么去完所有城市回到出发地经过的最短路程是多少?如果采用暴力求解的方法, 它的时间复杂度以指数级增长。人类目前还无法将TSP 问题转化为多项式时间复杂度的问题, 所以TSP 是NPC 问题。因此目前只可以采取近似求解的方法来寻找较优解。
以C作为求解TSP 问题的有序序列, 其中ci代表各个城市。假设共有n个城市,C=ci1,ci2,…,cin(i1,i2,…,in∈Z)。
以d作为按城市遍历序列C遍历完所有城市的距离,dij是lij的遍历相邻两城市之间的距离。
求解TSP 问题就是最终要求出一条有序序列C, 使得该序列拥有最小的d(即求出min∑dij)。
2 改进遗传算法求解TSP 问题
由于TSP 问题是完全NP 问题, 所以只有通过求近似最优解的求解算法来解决该类问题。如蚁群算法、模拟退火算法和遗传算法等。遗传是生物个体中都具有的功能, 它复杂且具有多样性。传统遗传算法在遗传基础上只继承了生物遗传中的交叉互换、基因突变、自然选择的大致框架而没有考虑到细胞具有遗传多样性。细胞在遗传过程中还存在多种行为, 如染色体的倒位、异位等。细胞外还存在病毒侵染生物细胞等行为。通过结合染色体倒位和病毒侵染行为来加深传统算法模拟生物遗传的程度, 实现对传统算法的优化以跳过局部最优解和加快收敛速度。
2.1 编码方式
路径编码是按照城市访问顺序排列的一种编码方式。通过随机产生不重复的遍历路径作为路径编码(染色体)可以将问题简化。以9 城市的TSP 问题为例, 编码方式如图1 所示。
2.2 初始化种群
融合遗传算法通过随机函数将城市点坐标排序打乱作为个体基因型。采用交叉遗传的方式, 选择迭代过程中最优(适应度最高)的个体的染色体为该算法的解。该条染色体的编码就是最终求得的近似最优遍历路线。以9 城市的TSP 问题为例, 其含n个个体的种群初始化如图1 所示。

图1 种群的初始化
2.3 初始化病毒种群
迭代开始之前设置初始基因为空的病毒种群(含m个个体),它通过复制初始优势个体基因以获得自身初始基因, 并与其他种群一同参与优胜劣汰。迭代开始前病毒种群侵染过程如图2 所示。

图2 初始病毒的侵染过程
在迭代开始之后, 每一轮迭代, 病毒种群都会优先以复制优势个体基因的方式侵染适应度较高[12]的个体以加快融合遗传算法的收敛。迭代开始之后病毒种群侵染过程如图3 所示。

图3 迭代开始之后病毒种群侵染过程
2.4 个体种群和病毒种群适应度的计算
定义1个体适应度: 个体在自然选择下的存活的能力(能力越大适应度越高, 反之则越低)。
根据个体基因越优异该个体越容易生存下去的原则, 即以个体的染色体所表示的遍历城市序列的总距离越小就越容易生存的原则, 建立适应度模型。种群中个体按序列顺序遍历城市后的总距离为Objv(n)。将总距离的倒数作为个体适应度函数。其中主个体适应度ffitness(n), 病毒个体适应度为ffitvirus(m)。主个体适应度一般表达式为

病毒个体适应度一般表达式为

根据遗传学原理, 当个体发生“进化”(其欧氏距离更小了)时, 个体的适应度就会提高。这样可以在不破坏算法的性能的情况下直接加快算法的收敛。
2.5 比例选择法进行自然选择
定义2比例选择法: 以一定比例进行自然选择的方法。
自然界中, 适应度高的个体不一定就不会被淘汰, 同理, 适应度低的也不一定会被淘汰。在该原理的基础上设定权重系数, 遵从适应度越高的个体被淘汰的概率越低, 适应度越低的个体被淘汰的概率越高的规则, 依照概率淘汰个体。
主个体选择系数: 基于每个个体的适应度函数所占总体种群适应度的比例来确定。个体的选择系数Pi表达式为
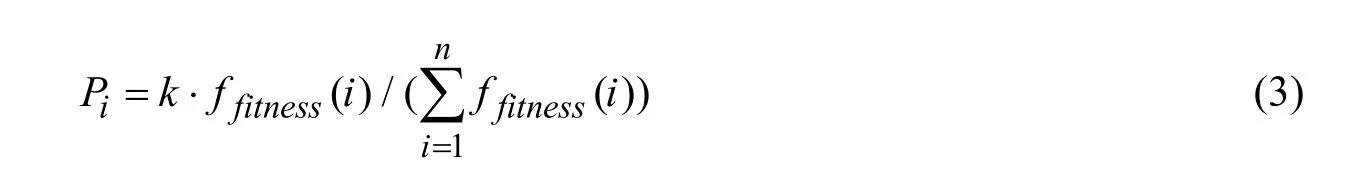
其中k为调整参数, 用于将Pi固定于区间[0,1]。
病毒选择系数: 由于每一代种群优势个体可能不同, 对于病毒种群, 将其侵染目标个体前的适应度fithostk和侵染目标个体后的适应度fithostk'之差作为该病毒种群的自然选择的概率系数Pv。其表达式为

其中kv为调整参数, 用于将Pi固定于区间[0,1]。
2.6 个体交叉和变异
由于简单地进行基因的复制和优胜劣汰不足以支持基因产生多样性。自然界中生物通过一定概率的染色体交叉互换、染色体的缺失、异位和倒位等行为构成了基因的多样性。基于该生物学原理, 解决该类TSP 问题的遗传算法通过设置交叉因子Pc和变异因子Pm让种群的染色体在遗传过程中进行交叉互换和变异[13]以产生新解, 从而模拟基因的多样性。
2.6.1 交叉
人体细胞在有丝分裂的四分体时期有概率会在同源染色体的非姐妹染色单体之间发生交叉互换的行为, 即染色体之间通过交换基因的片段获得新的基因。于是新旧基因一同参与优胜劣汰, 最终产生更适应环境的个体。
模拟这一行为, 遗传算法设置交叉因子Pc依概率交换基因的片段。由于每个城市出现的次数具有唯一性, 所以具体操作应该考虑以下情况:(i) 交换后的片段无重复基因: 直接进行交换;(ii) 交换后的片段中有重复基因时: 取消此次两个基因的交换。以图4 片段交换为例, 本次交换片段为个体1 的(5487)段和个体2 的(1678)段。由于片段中都包含基因7和基因8, 所以个体1 和个体2 的基因7 和基因8 位置互换, 其他基因位置不变。
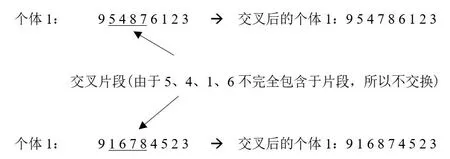
图4 交叉互换过程
2.6.2 变异
在自然界各个生物体中的基因的复制时期基因并不是每次都可以得到正确的复制, 复制错误就会产生新的基因。基因突变是物种多样性的重要来源。
遗传算法通过设置变异因子以模拟这一行为来进一步实现解的多样性。基本形式如图5所示。

图5 基因变异过程
2.7 染色体“倒位”(逆转)操作
生物学中还可以通过倒位操作来进一步丰富基因种类。在细胞分裂期, 染色体的某一片段会发生逆转, 从而产生新的基因型。本算法模仿自然生物学的染色体倒位操作[14], 算法基本步骤如下:(1) 随机挑选种群部分个体;(2) 随机生成染色体两个倒位点;(3) 对选中的染色体个体的倒位点中的基因进行逆转操作(见图6)。

图6 逆转操作
3 应用实例及评估
通过模拟75 个地点的仿真TSP 问题和34 个省会城市的实例TSP 问题, 来对比本文改进的遗传算法和传统遗传算法的相关性能。
3.1 初始实验环境及变量设置
本文的仿真实验在MATLAB 上进行。在同一个TSP 问题下, 分别用融合遗传算法L1和传统遗传算法L2进行仿真求解实验。通过对比2 个算法所求解的优越性、解收敛时的迭代次数和求解花费的时间来检验算法的有效性。
对于L1: 取初始种群系数S1=300, 交叉系数Pc=0.6, 变异系数Pm=0.1, 最大迭代系数gnmax=1 000。
对于L2: 取初始种群系数S2=250, 初始病毒种群系数S3=50,(保持总代数不变)交叉系数Pc=0.6,变异系数Pm=0.1, 最大迭代系数gnmax=1 000。
3.2 实验结果及分析
在该实验数据下, 迭代1 000 次的情况下, 融合遗传算法所求路径更加短暂, 并且在动态迭代视图中观察发现, 传统算法最优路径(见图7)在24、37、5、38 和23 等地点的路线成为了交叉路径(并非最优路径)并且基本保持不变, 可见传统算法易于陷入局部最优解, 从而验证了改进后的融合算法(见图8)加入了逆转操作从而更容易跳出“舒适圈”。
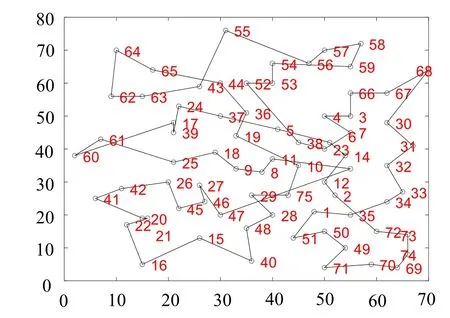
图7 传统算法路径
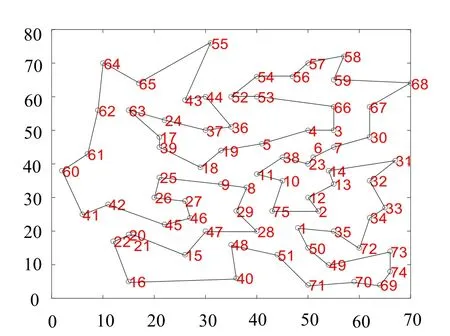
图8 融合算法路径
在仿真搜索最优解的过程中, 优化前的传统算法在800 代左右开始收敛(见图9), 而优化后的算法在450 代左右开始收敛(见图10)。

图9 传统算法搜索过程

图10 融合算法搜索过程
下面对多次实验的结果进行分析, 见表1(实验1~4: 传统算法; 实验5~8: 融合算法)。
由表1 数据可知, 仿真中优化算法达到最优解所需的迭代次数显著低于传统算法, 且优化算法得出的最优解较传统算法得出的最优解更为优越。

表1 仿真实验结果
关于迭代次数和平均运行时间的结果见图11 和图12。如图11、12 所示, 算法平均运行时间会随着迭代次数的增加而增加, 融合算法运行时间较传统算法运行时间稍多, 但得出的最优解对于传统算法有较大的差异。

图11 优化前后运行时间对比

图12 优化前后得出最优解对比
3.3 改进遗传算法与传统算法的实际应用对比
以34 个省会城市的TSP 问题为实例, 建立融合遗传算法模型和传统算法模型(相关参数与75 城市TSP 问题保持一致), 分别搜寻最优遍历方案。结果如图13~16 所示。

图13 融合算法最终轨迹图

图14 传统算法最终轨迹图

图15 融合算法优化过程

图16 传统算法优化过程
分析图13~16 可知, 虽然融合算法和传统算法都是在120 代左右开始收敛, 但传统算法陷入了局部最优解, 导致最终遍历序列并不是最优序列。从而验证了传统算法易陷于局部最优解的缺点。由于问题规模较小, 所以传统算法和融合算法的收敛代数基本一致。
4 结论
相对于传统的遗传算法, 本文将逆转操作和病毒侵染操作同时融入遗传算法以加快算法的收敛速度并使得遗传算法更容易跳出局部最优解。通过传统遗传算法和融合遗传算法的对比实验验证得到, 融合后的算法在解决规模大的TSP 问题时更容易跳出局部最优解, 拥有更优越的解。不仅如此, 它对比传统算法拥有更快的收敛速度, 即达到收敛所需的迭代次数更短。不足的是, 由于融合算法加入了新的循环函数, 导致运行时间成本增加了些许(75 规模的TSP 问题中平均运行时间增加了2 s 左右)。而通过优化暴力循环代码或采用CPU、内存利用率更高的高级程序语言如(C 语言)可以用于缩短算法运行时间。融合算法对于解决生活中复杂的物流运输、物资调用等问题[15]有重要参考意义, 也对其他启发式算法的融合操作提供了可借鉴之处。
