充填与垮落协同开采覆岩层间滑移破坏规律研究
2022-07-20郭宇鸣刘恒凤朱存利董超伟夏康祺
郭宇鸣,刘恒凤,殷 伟,朱存利,董超伟,夏康祺
(1.中国矿业大学 煤炭资源与安全开采国家重点实验室,江苏 徐州 221116;2.淮阴工学院 江苏省交通运输与安全保障重点实验室,江苏 淮安 223003)
0 引 言
近年来,随着绿色开采理念的提出,煤炭资源安全开采与环境保护协调发展被世人所提倡[1],固体充填开采技术则是实现绿色开采的重要途径之一,该技术可将矸石等固体废弃物充填采空区[2-4],达到置换“三下”压煤、保护地表建筑物及矿区环境的目的。为兼顾充填与采煤效率的双重目标,发挥综采高产高效与充填开采处理矸石的双重技术优势,充填与垮落协同开采技术应运而生,该技术是将固体充填开采技术与传统垮落法开采技术有机结合从而实现协同采煤的开采技术[5-7],即在一个工作面中包含充填开采和垮落开采2种开采方法。目前,对传统垮落法开采和固体充填开采覆岩移动规律的研究均已取得了丰硕的成果,具有代表性的成果:钱鸣高等[8]提出了关键层理论和砌体梁理论;史元伟等[9]分析了传统垮落法开采长壁工作面基本顶力学关系;赵晓东等[10]在岩层薄板理论系统工程级数求解方面的研究为岩层移动规律的进一步深入研究提供了新的途径;蒋金泉[11]采用薄板理论分析了基本顶的破断形式;李德海[12]用连续介质力学的方法,分析了开采煤层上覆层状结构岩层受开采的影响;刘东燕等[13]基于随机介质理论建立了承受非均匀荷载的等效复合岩梁模型,并对上覆岩层的层间剪切滑移进行描述;邓喀中[14]提出了开采沉陷的结构效应,并根据复合岩梁理论推导出开采沉陷中层面滑移函数和层面滑移判别式;肖岩等[15]针对组合梁受界面滑移效应的影响,进行了静力线弹性分析,提出了组合梁挠度计算的二阶算法;GIRHAMMAR等[16]给出了部分复合Euler-Bernoulli梁和梁柱的常微分方程及挠度和内部作用的通解。固体充填开采方面有:张吉雄等[17]推导出充填面支护强度力学关系式;黄艳利[18]对采空区充实率控制基本顶的作用进行了分析;李剑[19]建立了矸石充填采煤覆岩弹性地基叠层组合梁力学计算模型,得到上覆岩层的弯矩和挠度方程;王金安等[20]对采空区矿柱-顶板体系流变力学模型进行了研究;郭庆彪等[21]基于离散介质运移规律推导出固体密实充填开采的地表沉陷预测模型;郭忠平等[22]建立了充填体和上覆矩形薄板系统的力学模型,运用板壳理论和材料力学理论,给出了顶板最大下沉量计算公式等。
充填段向垮落段的不连续过渡将导致上覆岩层的倾斜变形并出现层间滑移效应,而现有研究缺少对覆岩层间滑移规律的揭示。笔者介绍了充填与垮落协同开采技术原理、工作面布置及工艺,并以平煤十二矿己15-31010协同工作面地质条件为背景,将协同开采工作面上方砂质泥岩(复合岩梁上层)和细砂岩(复合岩梁下层)视为双层复合岩梁,基于充填与垮落协同开采覆岩结构特征,建立协同开采工作面非均匀弹性地基复合岩梁滑移力学模型,采用Rayleigh-Ritz法求解方程,分析了协同开采工作面非均匀弹性地基双层复合岩梁挠度、滑移、弯矩和剪力分布规律及充填段复合弹性地基系数对四者的影响规律,同时采用物理相似模拟试验得出不同充实率条件下覆岩层间滑移规律,并对理论计算和物理模拟结果进行对比,验证了充填与垮落协同开采非均匀弹性地基双层复合岩梁力学模型的可靠性,为协同开采技术理论的发展提供基础。
1 充填与垮落协同开采技术
1.1 协同开采技术原理
充填与垮落协同开采技术将综合机械化固体充填与传统综采2套设备分段相接并协调布置于同一工作面内,实现采煤与充填作业同时高效进行[5]。其联合采用充填法和垮落法管理采场顶板,将工作面的充填段和垮落段首尾相接,实现采煤机的连续割煤。充填与垮落协同开采工作面具有兼顾充填、满足产能、保护环境、双重系统(充填、垮落)的特点。
1.2 协同开采工作面布置及工艺
协同开采工作面布置方式如图1所示,充填段布置充填液压支架、多空底卸式输送机、液压升降平台、充填物料转载机;垮落段布置传统液压支架;充填段和垮落段共用采煤机、带式输送机、刮板输送机;将充填段、垮落段设备和共用设备按照一定工序进行配合以实现整个工作面采煤与充填平行作业。
协同开采工作面只对充填段采空区进行充填作业,并在充填段支架移架拉直后实施充填,其将常规充填工作面的“一采一充(先采后充)”作业方式转变为“边采(垮落段采煤)边充(充填段充填)”,提高了充填效率、实现了采充并举。充填时通过分组控制落料孔的开合由机尾向机头方向充填;采煤工艺与传统垮落法类似(图1)。
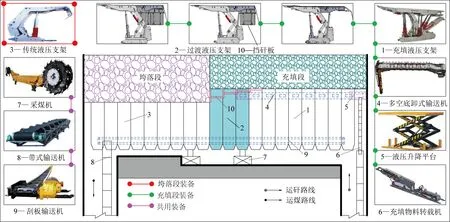
图1 协同开采工作面布置及设备Fig.1 Cooperative mining face layout and equipment
1.3 协同开采工程实例
试验矿井平煤十二矿位于河南省平顶山市东部,矿井采深达1 000 m,现主采己15煤层,煤厚2.9~3.5 m,平均厚3.2 m,平均倾角为5°,属于近水平煤层,赋存稳定。
为消耗矿井矸石,设计己15-31010工作面采用充填与垮落协同开采技术,考虑矸石处理需求和煤炭产量需求,设计协同面总长度为200 m,其中充填段长度120 m,垮落带长度为100 m(图2)。

图2 己15-31010协同工作面平面图Fig.2 Ji15-31010 cooperative mining face floor plan
2 协同开采覆岩移动与层间滑移分析
2.1 覆岩层间滑移力学模型
以平煤十二矿己15-31010协同工作面地质条件为背景,将协同开采工作面上方砂质泥岩(复合岩梁上层)和细砂岩(复合岩梁下层)视为两边固支的双层复合岩梁,充填段弹性地基是由断裂直接顶与采空区充填体共同组成的复合弹性地基[23-24],垮落段仅有断裂直接顶,即充填段与垮落段弹性地基不同,故可将协同开采工作面上方砂质泥岩和细砂岩视为非均匀弹性地基双层复合岩梁滑移力学模型,如图3、图4所示,其中工作面倾向为x轴,垂直向下为y轴,沿工作面走向为z轴,O点在垮落段与充填段分界位置,图中a为充填段长度,b为垮落段长度,q(x)为上部岩层载荷,p(x)为地基反力,u为层间滑移位移。
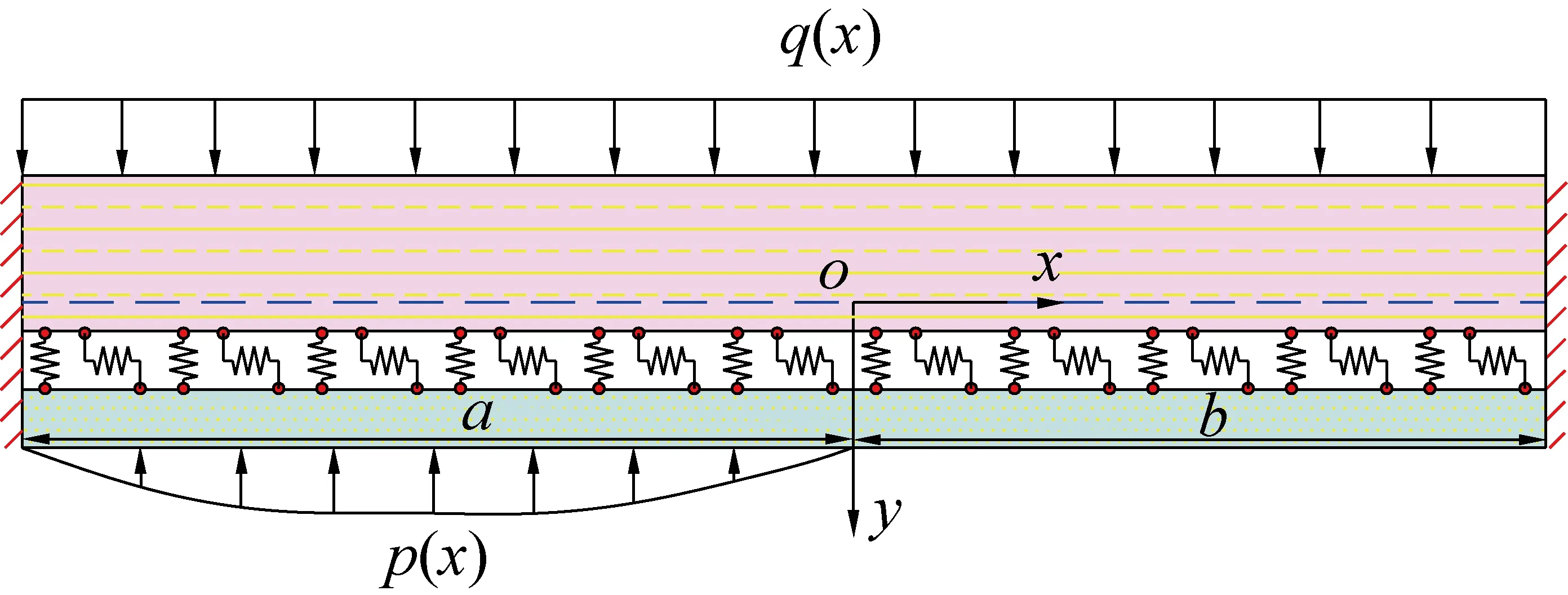
图3 非均匀弹性地基双层复合岩梁力学模型Fig.3 Mechanical model of double-layer complex rock beam on heterogeneous elasticity foundation
非均匀弹性地基的概念是根据实际工程条件提出的,如高层建筑筏板基础的地基、含有填充物质的地基等,其地基往往在水平方向上表现出非均匀性,因此,为了更好地符合工程实际,通常情况下可以把弹性地基系数假设为水平方向位置x的函数,而并非常量。常用的有非均匀Winkler弹性地基模型,其地基反力表达式[25]为
p(x)=ki(x)w(x)
(1)
其中:ω(x)为挠度方程;i=1,2,协同开采工作面非均匀弹性地基梁力学模型是采用分区域变化弹性地基系数的方法表达非均匀Winkler弹性地基对双层复合岩梁的作用,区域划分为充填段k1(x)和垮落段k2(x),其中k1(x)表示充填段基本顶下方破断直接顶与充填体紧密接触后所形成组合体的复合弹性地基系数。表达式[26-27]为
(2)
式中:kz为直接顶弹性地基系数,N/m3;kc为充填体弹性地基系数,N/m3;hz为直接顶厚度,m;hc为充填体高度,m。
取图3中的双层复合岩梁固定端微单元dx分析滑移剪切特征,如图4所示。

图4 非均匀弹性地基双层复合岩梁微单元Fig.4 Micro unit of double-layer complex rock beam on heterogeneous elasticity foundation
当岩梁交界面处的剪切应力大于界面允许剪应力时,双层岩梁发生层间滑移,在荷载作用下双层岩梁发生弯曲下沉,上、下层岩层分别产生弯曲,假设双层岩梁交界面不发生明显离层位移,可得岩层间滑移位移函数du的微分方程[28]为
du=2h1w″(x)
(3)
式中,h1为复合岩梁上层岩层厚度,m。
协同开采包括充填法和垮落法2种,在充分考虑到两者对双层复合岩梁控制特点的条件下,根据边界条件和覆岩结构特征设双层复合岩梁挠度方程为
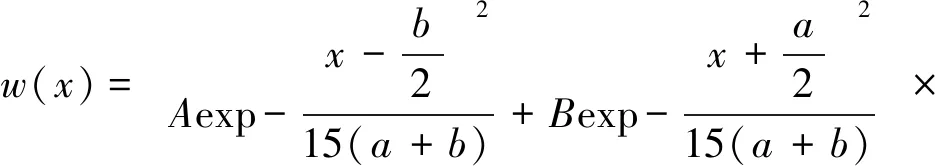
(4)
式中:a为充填段长度,m;b为垮落段长度,m;其作为尺寸参数,具有调节挠度方程特征的性质。
挠度方程的求解采用Rayleigh-Ritz法[29],组合梁形变势能为:
(5)
式中:Vs为上岩层积分区域;Vx为下岩层积分区域;Es与Ex为双层复合岩梁上下岩层弹性模量,Pa;ξs为双层复合岩梁上岩层总应变;ξx为双层复合岩梁下岩层总应变,表达式为:
(6)
式中:Ss为双层复合岩梁上岩层横截面积;Sx为双层复合岩梁下岩层横截面积。
充填段载荷产生的外力势能Vc包括覆岩载荷产生的势能加上充填体对双层复合岩梁支持引起的势能,垮落段载荷产生的外力势能Vk仅包括覆岩载荷产生的势能,Vz为充填段和垮落段载荷所产生的总外力势能即:
(7)
双层复合岩梁上下岩层相对滑移产生的滑移势能Uh为
(8)
其中:ks为双层复合岩梁的等效平均滑移刚度;u(x)为双层复合岩梁滑移公式。双层复合岩梁总势能П=W+Vz+Uh,即:
(9)
根据最小势能原理,总势能变分为0,联立可解出A和B的值,驻值条件:
(10)
求出A和B则得出双层复合岩梁挠度方程,基于弹性理论挠度与弯矩与剪力的关系,求出双层复合岩梁弯矩与剪力方程。
2.2 弹性地基系数对双层复合岩梁整体变形影响规律
根据平煤十二矿工程地质条件,煤层埋深H=1 km,煤层倾角5°,平均煤厚3.2 m,充填段长度a=120 m,垮落段长度b=100 m,砂质泥岩(复合岩梁上层)h1=6.5 m,细砂岩(复合岩梁下层)h2=2.5 m,通过实验室实测得砂质泥岩弹性模量Es=10.6 GPa,细砂岩弹性模量Ex=13.5 GPa,复合弹性地基系数取值详见表1。
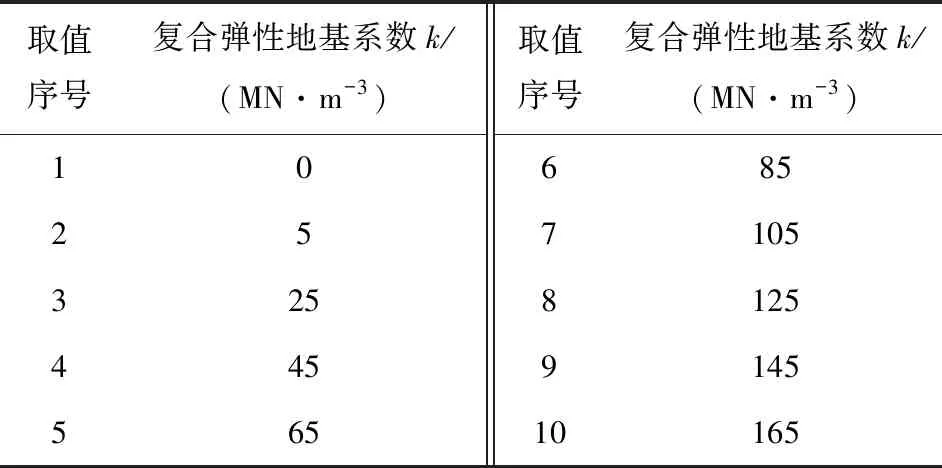
表1 复合弹性地基系数取值Table 1 Value of coefficient of elasticity foundation
将上述参数代入式(1)—式(10)可求解出双层复合岩梁挠度方程、滑移方程、弯矩方程和剪力方程,如图5所示。
协同开采双层复合岩梁变形与内力分布曲线如图5所示,由图5可知:协同开采双层复合岩梁变形和内力的分布规律与垮落开采和充填开采均不相同且更为复杂,其主要是因为协同开采中充填开采和垮落开采相互影响导致协同开采覆岩移动变形发生了突变,其突变规律表现为:
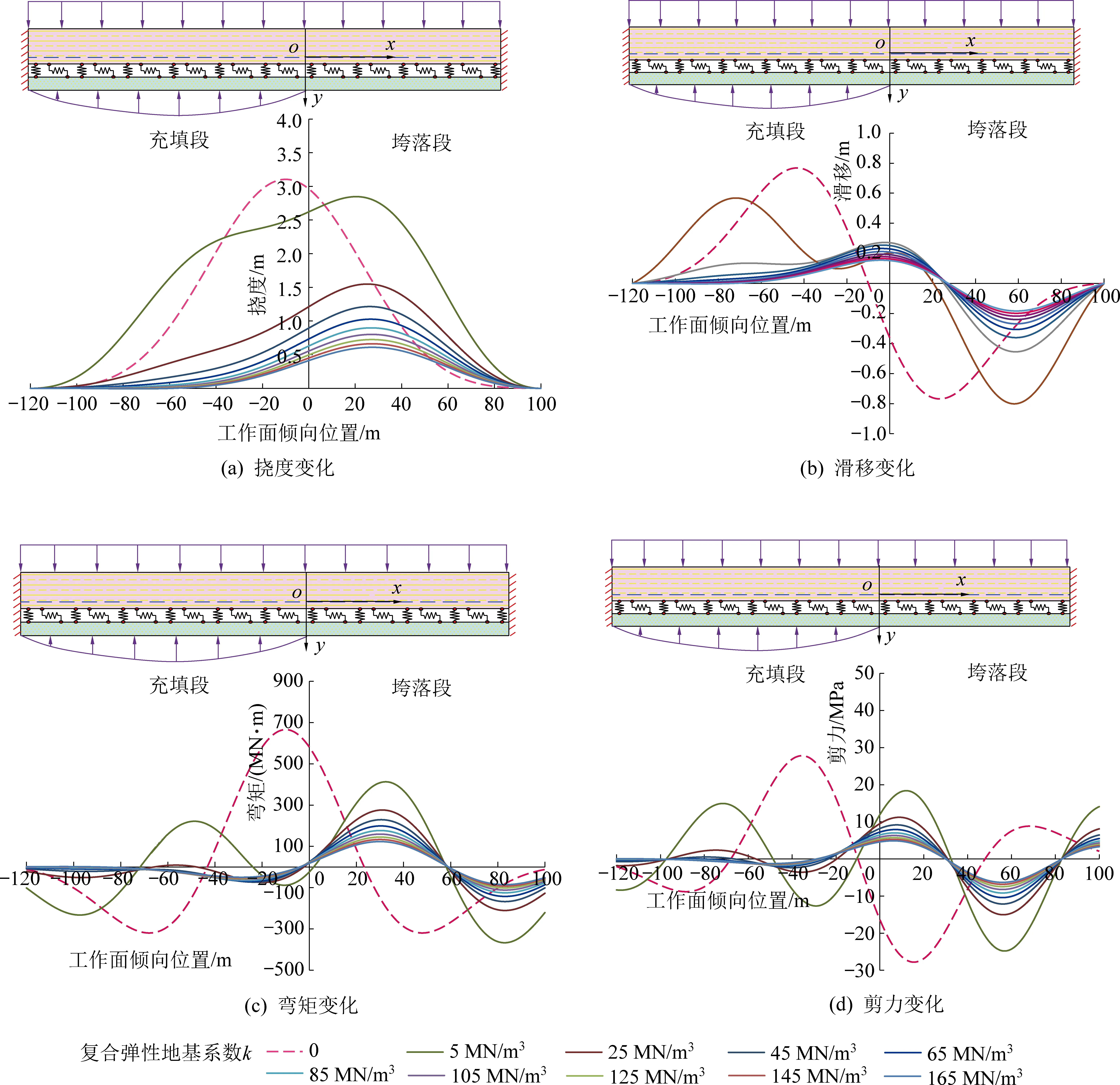
图5 协同开采双层复合岩梁变形与内力曲线Fig.5 Deformation and internal force curve of double-layer complex rock beam in collaborative mining
1)挠度曲线由单个开采方法的单驻点偶函数分布突变为协同开采的“勺状”非对称分布,在工作面长度范围内峰值个数未发生变化,但出现了峰值偏移的现象,即随着充填段复合弹性地基系数的增大挠度峰值从工作面中间位置移动到垮落段25 m左右处。
2)滑移曲线由单个开采方法的双驻点奇函数分布突变为非对称性分布,当充填段复合弹性地基系数较低时滑移曲线会出现3个峰值,位置分别位于充填段的-70 m、垮落段的1.6 m和58 m,当充填段复合弹性地基系数较高时滑移曲线又变成2个峰值,位置分别在充填段的-3.9 m和垮落段的59 m,即滑移曲线随着充填段复合弹性地基系数的增大会从2个峰值转变为3个峰值最后恢复两个峰值状态,垮落段的1.6 m和充填段的-3.9 m为充填段与垮落段的接触位置,因此无论k如何变化两段接触附近滑移均表现较为明显。
3)弯矩分布由单个开采方法的三驻点偶函数分布突变为协同开采的非对称波浪形分布,峰值个数从原来的3突变为5之后又恢复到3,当充填段复合弹性地基系数较低时5个峰值的位置分别为充填段的-96、-47和-10 m与垮落段的35.8 m和84.5 m 左右,当充填段复合弹性地基系数较高时三个峰值的位置分别在充填段的-28 m与垮落段的32 m和83 m左右,岩梁破断的位置会首先发生在最大的峰值位置,该处位置在垮落段34 m附近。
4)剪力分布由单个开采方法的四驻点奇函数分布突变为非对称波浪形分布,峰值个数随着k的改变首先没有发生变化,之后降为3个峰值,当充填段复合弹性地基系数较低时4个峰值位置分别为充填段的-70 m和-32 m与垮落段的10 m和58 m,当充填段复合弹性地基系数较高时4个峰值位置分别在充填段的-50 m与垮落段的10 m和59 m。
从上述分析可知协同开采覆岩挠度方程、滑移方程、弯矩方程和剪力方程驻点数(峰值数)和奇偶性随着充填段复合弹性地基系数k的变化均会发生突变,且峰值大小随着k的增大而减小,较单个开采方法的覆岩挠度、滑移、弯矩和剪力分布更为复杂。
2.3 弹性地基系数对双层复合岩梁分段变形影响规律
根据上述计算结果取协同开采双层复合岩梁挠度、滑移、弯矩和剪力四者的统计数值—平均值、最大值、最小值,分析协同开采双层复合岩梁在不同复合弹性地基系数下四者的变化规律,四者统计数值随不同充填段复合弹性地基系数变化如图6所示(图中第一个字母B为充填段、C为垮落段,第二个字母ω为挠度、u为滑移、M为弯矩、Q为剪力,第三处字符表示统计数值类型ave为平均值、max为最大值、min为最小值,如B-ω-ave为充填段挠度平均值图中68.75%和93.75%的充实率为划分快速降低区、缓慢降低区、平稳区的临界值,此外,由于充实率是直接影响复合弹性地基系数的因素,所以该充实率彩轴与横轴复合弹性地基系数为平行对齐的关系)。

图6 协同开采双层复合岩梁统计数值变化Fig.6 Statistical variation curve of double-layer complex rock beam in collaborative mining
协同开采双层复合岩梁挠度、滑移、弯矩和剪力四者统计数值随着充填段复合弹性地基系数k的变化具有一致性,即随着k的增大四者统计数值的绝对值逐渐降低,但降低幅度在逐渐减小,可将统计数值变化曲线划分为快速降低区、缓慢降低区和平稳区。其中,快速降低区对应k的范围:0≤k<25 MN/m3;缓慢降低区对应k的范围:25≤k<125 MN/m3;平稳区对应k的范围:k≥125 MN/m3。因此在快速降低区内参数降低速度较大,即充填段复合弹性地基系数k的微小变化可引起协同工作面整个双层复合岩梁变形和内力较大的改变,在缓慢降低区和平稳区,充填段复合弹性地基系数的变化对双层复合岩梁变形和内力的变化影响较小,因此在实际生产过程中应将充填段弹性地基系数k保持在缓慢降低区与平稳区内,可降低协同开采工作面双层复合岩梁的变形和内力分布,减缓因采矿作业引起的扰动。另外从图7(0≤k≤165 MN/m3内的变化幅度)中可以看出,充填段复合弹性地基系数对充填段统计数值变化幅度影响均大于垮落段统计数值的变化幅度,且垮落段各统计数值的绝对值均大于充填段各统计数值的绝对值。图7中内部各个短横条内标示数值含义为对应参数随复合弹性地基系数变化而产生的变化幅度。
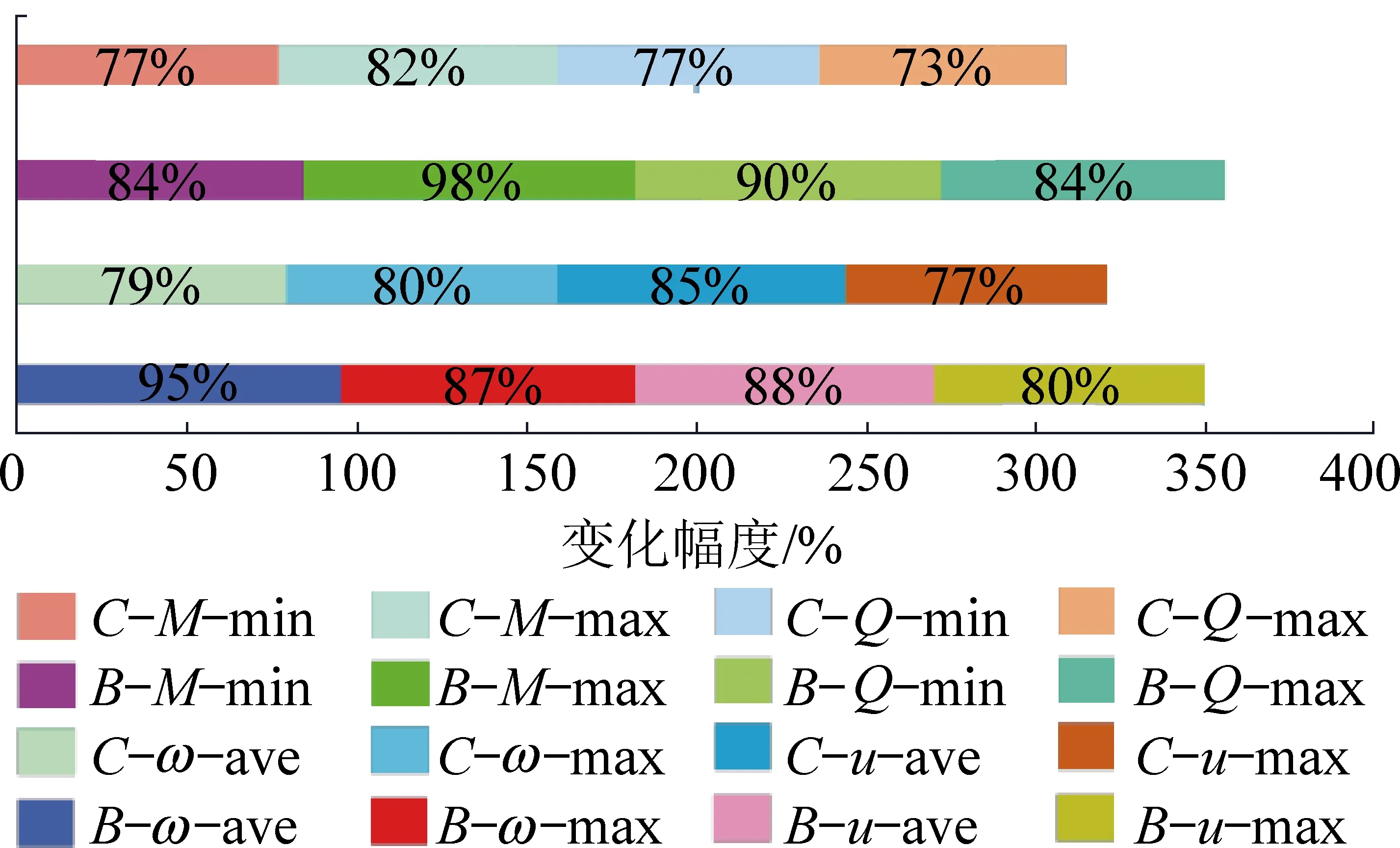
图7 复合弹性地基系数影响各因素变化幅度Fig.7 Magnitude of change in each factor influenced by the composite elastic foundation factor
充填体弹性地基系数k与充实率φ的关系式见式(11)[30]
(11)
式中:q为覆岩载荷,N/m2;h为采高,m;k为弹性地基系数,N/m3。
通过实验室测试可知协同开采工作面双层复合岩梁极限弯矩为56.333 MN·m,以该数值为B-M-max可计算出充填段复合弹性地基系数为125 MN/m3,则充填段临界弹性地基系数为125 MN/m3,当充填段充弹性地基系数大于125 MN/m3时,充填段双层复合岩梁不会断裂,协同开采工作面双层复合岩梁断裂只发生在垮落段,将k=125 MN/m3代入到式(11)中计算出充填段临界充实率为93.75%,比文献[31]计算出的充填段临界充实率92.55%增加了1.2%,因此将滑移理论应用到协同开采中,可提高安全系数。另外充填段最大弯矩位置靠近在-28 m处,距离垮落段较近,其主要原因是垮落段双层复合岩梁的高应力水平影响到充填段双层复合岩梁的应力分布,导致充填段临界充实率大于单一充填开采要求的临界充实率。另外即使充填段复合弹性地基系数达到原煤体弹性地基系数时,充填与垮落协同工作面双层复合岩梁仍会断裂,破断位置发生在垮落段的34 m左右处。
3 不同充实率协同开采覆岩移动与层间滑移分析
采用物理相似模拟的方法通过改变充填段不同充实率研究充填与垮落协同开采条件下覆岩层间滑移规律,物理相似模拟的几何相似比为1∶100,应力相似比为1∶166.7,容重相似比为1∶1.67,模型尺寸(长×宽×高)为2.5 m×0.2 m×1.5 m,模型上方加载0.135 MPa的补偿应力,根据实际地质情况和实验室测试得到模型力学参数并确定材料配比,详见表2。
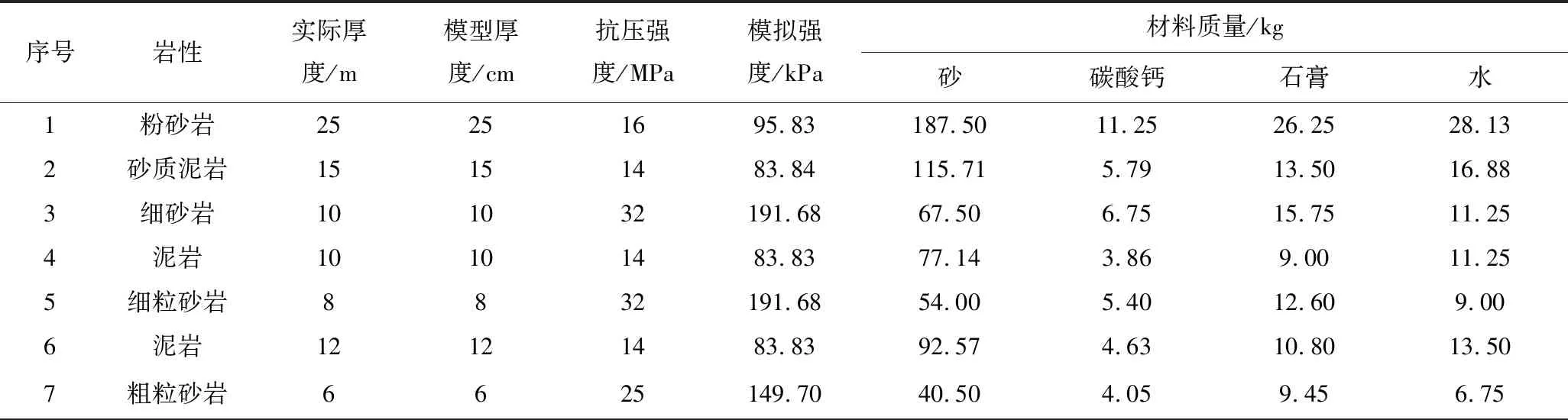
表2 煤岩层力学性能参数及材料配比Table 2 Mechanical property parameters and material ratio of coal strata and rock stratum

续表
充填与垮落协同工作面覆岩层间滑移与变形监测的仪器为Matchid2D非接触式应变测量系统。充填体的相似模拟材料是采用海绵、纸张、薄塑料、厚塑料、木板(1mm厚)等材料组合相似材料[32]。物理模拟实验系统包括相似模拟实验平台、载荷补偿装置、高速摄像机以及Matchid2D软件,物理模拟实验系统如图8所示。

图8 物理相似模拟实验系统Fig.8 Physical similarity simulation experiment system
利用 Matchid2D 软件计算出不同充实率条件下覆岩移动下沉及岩层层间滑移量,通过筛选加工得出基本顶下沉值及层间滑移值,绘制出充填与垮落协同开采工作面复合岩梁在工作面倾向位置基本顶下沉及滑移曲线,如图9和图10所示。

图9 基本顶下沉曲线Fig.9 Basic roof subsidence curve
由协同开采物理相似模拟实验测试曲线图10可知:协同开采工作面直接顶与基本顶组成的复合岩梁下沉与滑移曲线分布均发生了突变,与单一充填和单一垮落开采的下沉与滑移曲线分布均不相同,其中充填段复合岩梁下沉均值和最大值随着充实率的增大而逐渐降低,下沉均值依次为1.51、0.94和0.49 m,最大值为1.98、1.24和0.67 m,最大值位置在工作面充填段与垮落段接触位置(120 m左右);而垮落段下沉均值和最大值并不随着充实率而产生较大的改变,下沉均值分别为1.71、1.75和1.61,最大值为3.05、3.11和2.93 m,最大值位置在垮落段中心点。

图10 协同开采物理相似模拟实验测试曲线Fig.10 Test curve of physical similarity simulation experiment for collaborative mining
图11为图8截取位置开采前后放大图,在截取位置有五层岩层出现4条滑移面(1号~4号),位置对应岩层层面位置,对图中的散斑进行标号(1号~120号),选取图中处于滑移面位置的5个散斑14号、40号、50号、75号和79号,对比分析开采前后选取的5个散斑形状变化可知:岩层层间发生了明显的滑移现象,这是由于工作面上覆岩层受到采动影响,岩层之间发生剪切破坏,同时覆岩伴随着弯曲下沉,即覆岩在受到开采的影响会产生水平和竖直方向上的移动,合运动为转动,对于两层直接接触的岩层,上下层岩层分别向相反方法发生滑移,上层岩层向后方移动,下层岩层向前方移动(图11中数字为标示特征点,方便对比特征点的位置变化情况)。

图11 截取位置开采前后对比Fig.11 Comparison before and after mining of selected position
滑移曲线较单一开采方法的对称分布[33]突变为非对称分布,充填段滑移均值与最大值随着充实率的增加而降低,垮落段滑移均值与最大值同样随着充实率的增加而降低,充填段滑移均值依次为:0.067、0.054和0.051 m,最大值依次为:0.15、0.125和0.112 m,位置同样在充填段与垮落段接触位置(120 m左右);垮落段均值依次为:0.069、0.061和0.053 m,最大值依次为:0.25、0.206和0.168 m,最大值位置在垮落段中心点。协同开采工作面由于受到充填段充填体的影响,导致整个工作面覆岩下沉与滑移均发生了突变,充填段下沉值与滑移值均小于垮落段两者的大小,且充填段滑移随着充实率的改变变化较为显著,垮落段随着充实率的变化改变不大。同时充填段滑移较垮落段变化复杂,当充实率从70%增加到85%时,在充填段0~80 m滑移曲线产生了较大变化,从双峰突变为单峰,但最大滑移位置并没有发生变化,可知充填段与垮落段接触位置覆岩移动较为复杂,实际工程中应注意两者接触位置的覆岩运移情况。
4 理论计算与物理模拟对比分析
为了验证理论计算的准确性,将力学计算得出的滑移曲线和物理相似模拟得到的滑移曲线进行对比分析,得到图12所示的力学计算滑移曲线与物理模拟滑移拟合曲线对比图。

图12 力学计算与物理模拟滑移拟合曲线对比Fig.12 Comparison diagram of slip fitting curve between mechanical calculation and physical simulation
由图12和表3可知:物理相似模拟得到的滑移拟合曲线(R2=0.958 4、R2=0.969 4、R2=0.953 5)与力学计算得出的滑移曲线的分布规律大致相同,两者层间滑移曲线均分为正负2个区域,其中,充填段为正,垮落段为负,即充填段与垮落段均向两者接触位置即协同工作面中间位置移动,且充填段滑移最大值均小于垮落段滑移最小值的绝对值,充填段滑移曲线变化较垮落段复杂。从图中可知两者得出的滑移曲线吻合的较好,相似度较高,可知力学计算的结果较为准确可靠,可将该模型应用到实际同类采矿工程中。
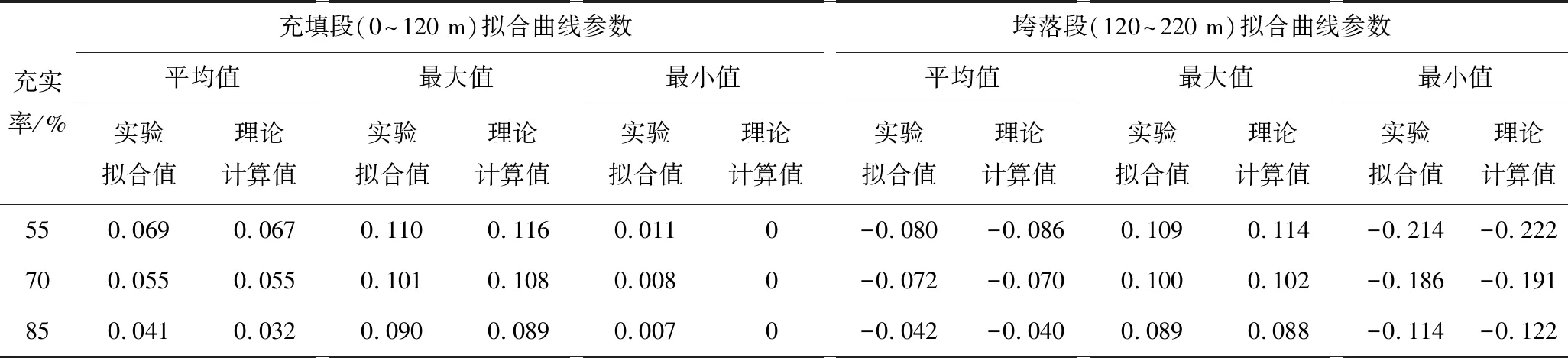
表3 力学计算与物理模拟滑移拟合曲线参数对比Table 3 Comparison of parameters of slip fitting curve between mechanical calculation and physical simulation
5 结 论
1)基于充填与垮落协同开采技术原理,建立了协同开采工作面非均匀弹性地基双层复合岩梁滑移力学模型,所得出的协同开采覆岩挠度、滑移、弯矩和剪力方程的分布情况会因充填段复合弹性地基系数k的变化而发生突变,较单一开采方法更为复杂。
2)分析了充填段复合弹性地基系数k对协同开采双层复合岩梁变形与内力的影响规律:协同开采工作面双层复合岩梁四者方程驻点数(峰值数)和奇偶性随着充填段复合弹性地基系数的变化均会发生突变,且峰值大小随着k的增大而减小,较单个开采方法的双层复合岩梁变形与内力分布更为复杂。
3)根据协同开采双层复合岩梁挠度、滑移、弯矩和剪力统计数值与k的关系,得出四者统计数值的绝对值随k的增大而逐渐降低,可划分为快速降低区、缓慢降低区和平稳区。在快速降低区内,k的微小变化可引起双层复合岩梁变形和内力较大的改变,即在实际生产中应将k保持在缓慢降低区或平稳区内,减缓采矿作业引起的扰动。
4)计算出协同开采充填段临界弹性地基系数为125 MN/m3对应充实率为93.75%,比文献[31]计算出的充填段临界充实率92.55%增加了1.2%,由于垮落段高应力水平的影响导致协同开采充填段临充实率高于单一充填开采的临界充实率。
5)由物理模拟得出直接顶与基本顶组成的双层复合岩梁下沉与滑移分布规律,经过理论计算与物理模拟可知充填段与垮落段覆岩均向协同工作面中央位置移动,且两者得出的滑移曲线吻合的较好,知该双层复合岩梁滑移力学模型适合描述采场覆岩层层间滑移规律。
