含水煤体纵波波速变化规律试验研究——以古汉山烟煤与赵固无烟煤为例

李东会，梁雁侠，张 凯，王晨曦

(1.河南理工大学 安全科学与工程学院，河南 焦作 454000；2.中原经济区煤层(页岩)气河南省协同创新中心，河南 焦作 454000)

0 引 言

声波测试煤岩介质物理力学特性及结构特征是通过记录超声波穿透煤岩信号参数(如波速、振幅、衰减因子等)变化，间接地了解煤岩的物理力学特性及结构特征，在煤矿安全开采中得到广泛应用[1-2]。煤是一种多孔介质，而井下煤层由于地下水、水力增透技术等因素导致煤体内部含水程度不同，不同含水程度的煤层对其力学特性和瓦斯在煤层中流动有着较大的影响，从而会造成瓦斯抽采的困难。为解决含水煤层条件下瓦斯不易解吸、煤层渗透率低而造成的瓦斯抽采困难的难题，利用声波测试技术来预测煤层含水饱和度的方法是可行的。因此，本文在实验基础上,研究了纵波波速随含水饱和度的变化规律,并解释了该变化规律的内在机理。为声波资料应用于煤层含水饱和度评估与预测提供了理论基础,对不同饱和度煤层评价都具有重要意义。

近年来学者针对岩石声波在不同含水饱和度传播变化规律进行了大量研究。WYLLIE、BIOT、GREGORY等[3-5]最早研究岩石纵波波速与不同含水饱和度的变化规律，得出岩石孔隙均匀分布时，随饱和度增加纵波波速增大。AMOS[6]对岩石进行干燥与饱水状态下的声波测试，得出岩石含水对纵波影响较大，对横波影响较小。LOUIS[7]首次提出岩石水力学这一岩石含水特性的力学名称。之后国内外学者对岩石含水进行了大量的研究。国内学者从20世纪80年代开始研究，孙成栋[8]最先进行了岩石试件的S波测试技术。赵明阶等[9]给出岩石变形参数的测试方法，把波速与工程岩体分类联系起来。周治国等[10]、史謌等[11]、陈旭等[12]对不同岩样进行了不同含水率声波测试，得出岩石弹性波速度和含水饱和的关系。段天柱等[13]研究受载条件下不同含水率砂岩力学特性及波速规律。

研究煤体不同含水率的少之又少。李楠、王云刚、赵宇等[14-16]研究煤样吸水率对声波速度的影响，他们分析了干燥和饱水状态煤样声波的变化规律，得出相应的结论。但不同含水率煤样声波变化规律试验分析的很少。因此在研究岩石不同含水饱和度声波变化规律的基础上，研究煤样不同含水饱和度声波变化规律，为煤层物理勘探提供室内试验依据。

1 试验方案

1.1 煤样制作

采用古汉山烟煤与赵固无烟煤为研究对象。首先，将新鲜大块煤体从井下采出并立即用胶带将其捆扎严密，保证煤体得到密封；其次，将煤体尽快运至井上，并立即采取浸蜡固封的方法再次进行密封。根据测量的结果，合理规划如何钻取岩芯，用粉笔划分界线，并记录清晰，然后在切割机上面切割煤块；操作切割机，要确保安全，切煤的时候下刀要连续，稳定。为了保证加工的时候样品稳定，试样尽量有平整断面。煤样的制取是以平行层理及垂直层理方向。煤体式样加工成直径50 mm，高100 mm的圆柱体样品，钻取古汉山与赵固煤样各2组。参数见表1。

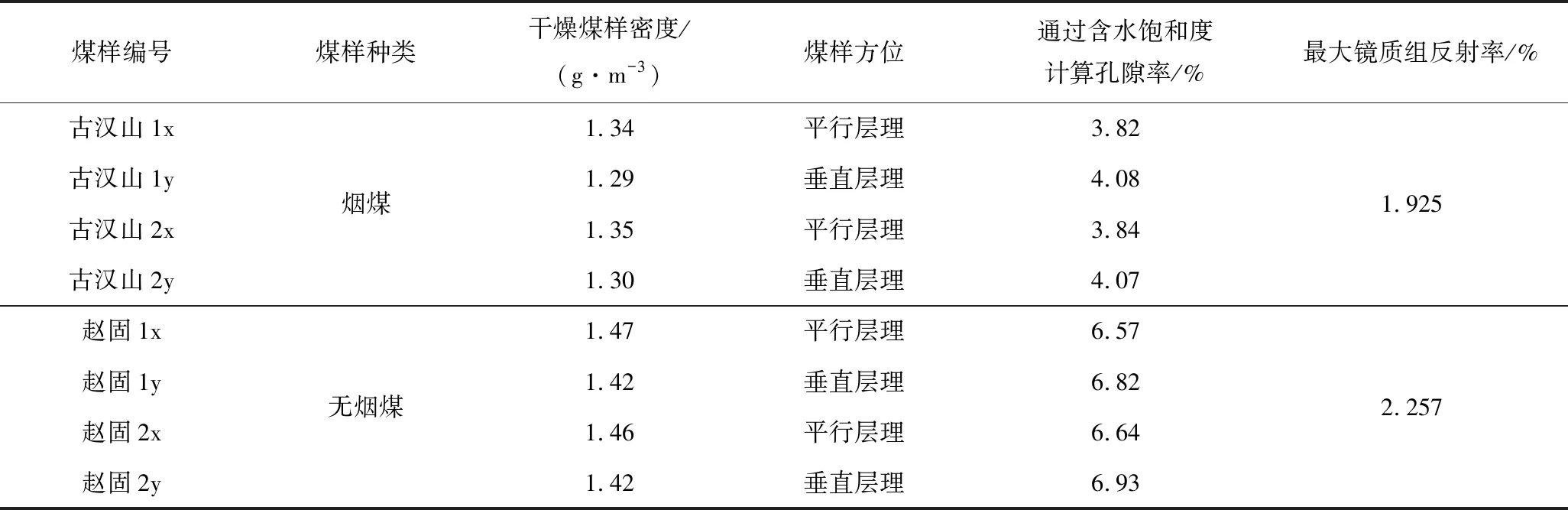
表1 煤样参数Table 1 Basic parameters coal samples

煤样自然吸水处理过程：① 将煤样放入105～110 ℃的干燥箱24 h，取出放入干燥器中冷却室温称重mdry；② 将煤样浸泡在水中使其自由吸水，期间不定时测量不同含水饱和度下试样下的质量m；③当试样含水基本保持不变，每隔24 h称量1次，直到连续3次测量质量差不超过0.01 g为止，最后一次为自然吸水饱水质量msat。

1.2 试验含水饱和度Sr和煤样孔隙率ρ计算方法

(1)

(2)

式中：ρL为水的密度，取1g/m3；V为试样体积；φ为孔隙率。

1.3 不同含水饱和度波速计算方法

选用换能器发射频率为50 kHz，采用适量凡士林耦合煤样与换能器端面。不同含水饱和度波速v=L/T，L为试样长度，m；T为超声波传播时间，s。

2 试验结果与分析

2.1 波速与含水饱和度变化规律

为研究不同煤质含水煤体波速变化情况，选取古汉山烟煤、赵固无烟煤进行试验，分别进行试验4组，分别测试8个煤样不同含水饱和度声波波速(表2、表3)。

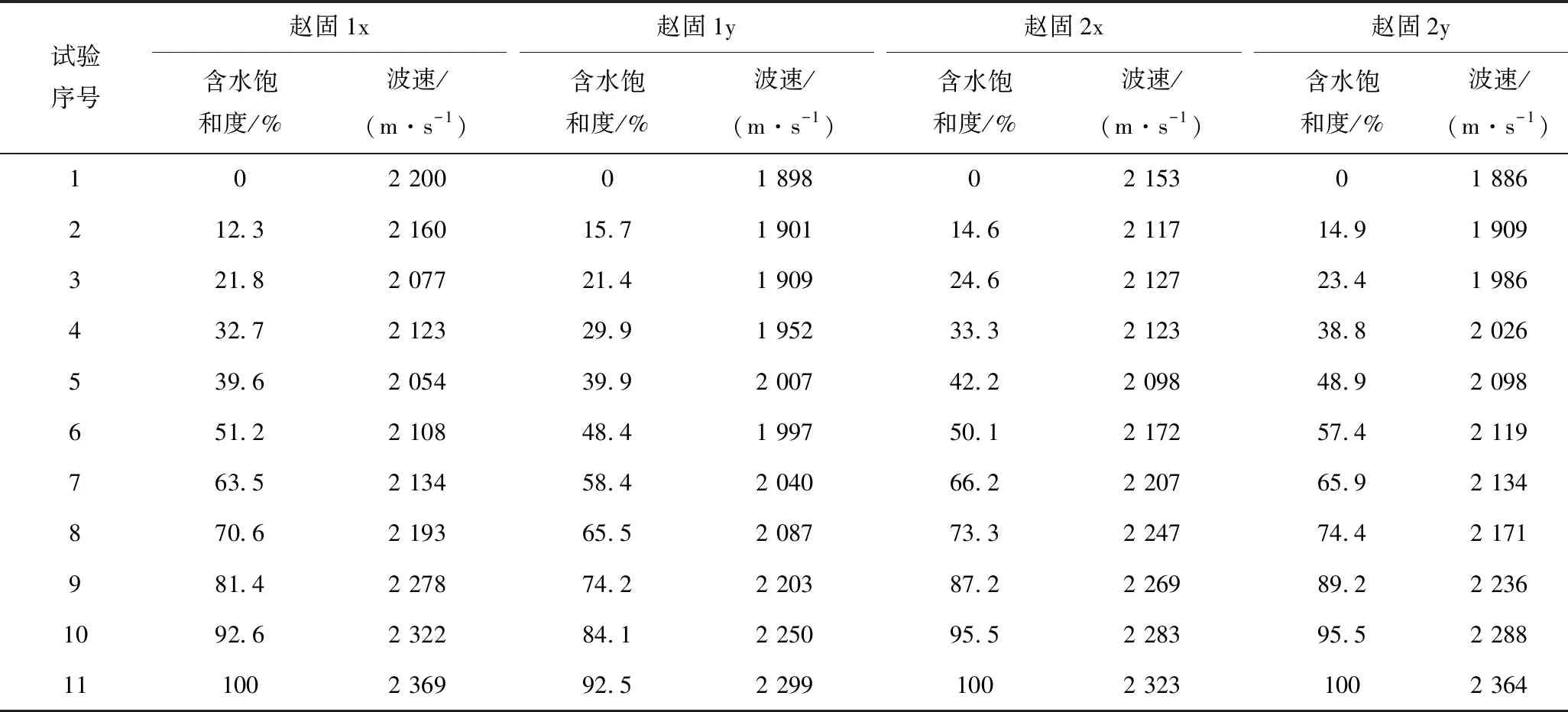
表2 赵固煤样不同含水饱和度波速Table 2 Wave velocities of Zhaogu coal samples with different water saturation

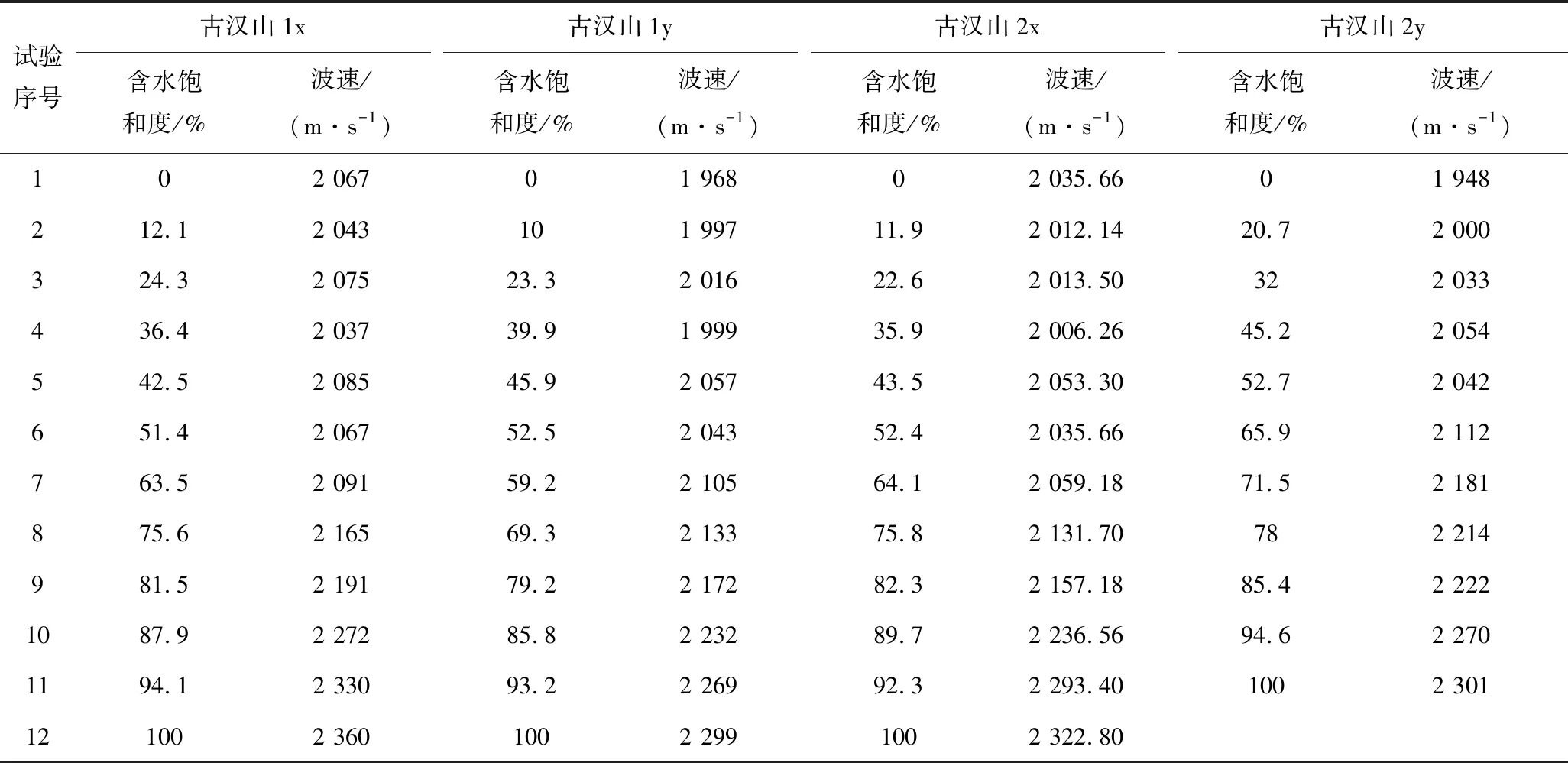
表3 古汉山煤样不同含水饱和度波速Table 3 Wave velocities of Guhanshan coal samples with different water saturation

通过对以上数据分析，赵固、古汉山2组煤不同含水饱和度具有相同的变化规律，因此，以赵固1x、1y，古汉山1x、1y一组为例进行分析，得出结论如图1所示。

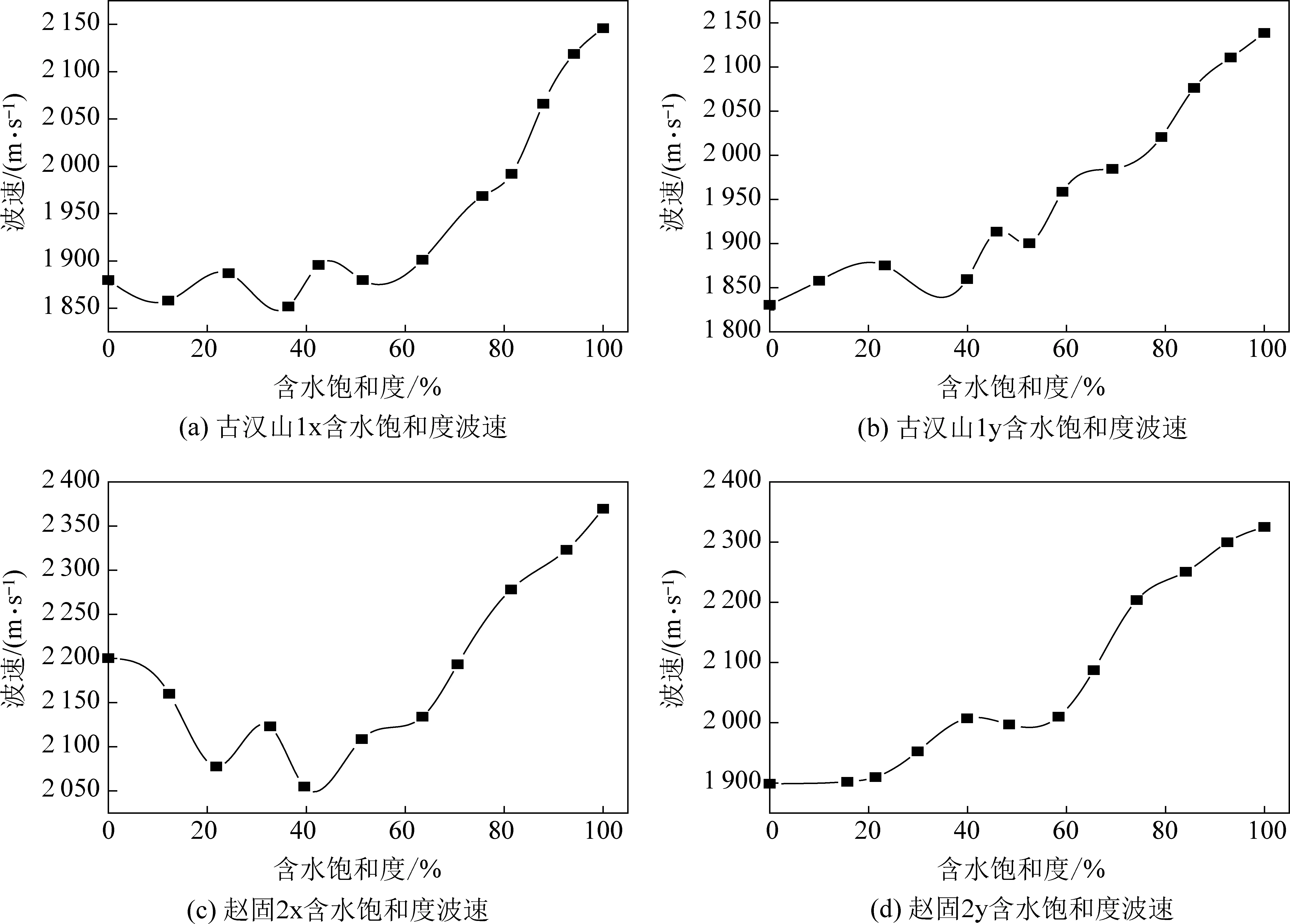
图1 古汉山、赵固煤样含水饱和度变化规律Fig.1 Variation law of water saturation of Guhanshan and Zhaogu coal samples

由图1可得：无论是古汉山烟煤还是赵固无烟煤，在含水饱和度60%之前平行层理波速随着含水饱和度增大而减小，期间有波动。含水饱和度在60%以后波速随含水饱和度增加而快速增大。而垂直层理整体随煤体含水饱和度增大而增大，在含水饱和度在60%之前增加缓慢，到60%以后波速随含水饱和度增加而快速增大。且无烟煤平行层理垂直层理波速大于烟煤平行层理垂直层理波速。是由于无烟煤变质程度高于烟煤，声波在煤体传播衰减、散射低，导致波速传播快。

2.2 波速与含水饱和度关系研究

为了描述了波速与不同含水饱和度二者之间的关系。采用基于Wood理论的Gassmann[17]方程，如下所示：

(3)

其中，

KG=Km+α2M

(4)

(5)

(6)

(7)

(8)

r=ρd+φ[SrρL+(1-Sr)ρa]

(9)

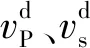
KS=Km(1+50φ)

(10)

根据Wood理论假设，则

(11)

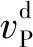
如图2所示，红色线条为基于Wood理论假设的Gassmann方程。无论是古汉山烟煤还是赵固无烟煤在平行层理在含水饱和度60%之前，实际波速与Wood理论假设的Gassmann方程基本吻合，上下偏差不大。是因为在进水最初阶段，样品的进水率大。平行层理煤体孔隙率小，当样品从完全干燥状态到较小的饱和度时，干燥的煤体与水之间会发生物理和化学作用，使煤体发生化学软化，导致煤体弹性模量下降，使弹性波衰减增大，波速减小。当含水饱和度在10%～60%时，波速变化较小，且无规则，此时弹性波按Wood理论的Gassmann方程发生变化。

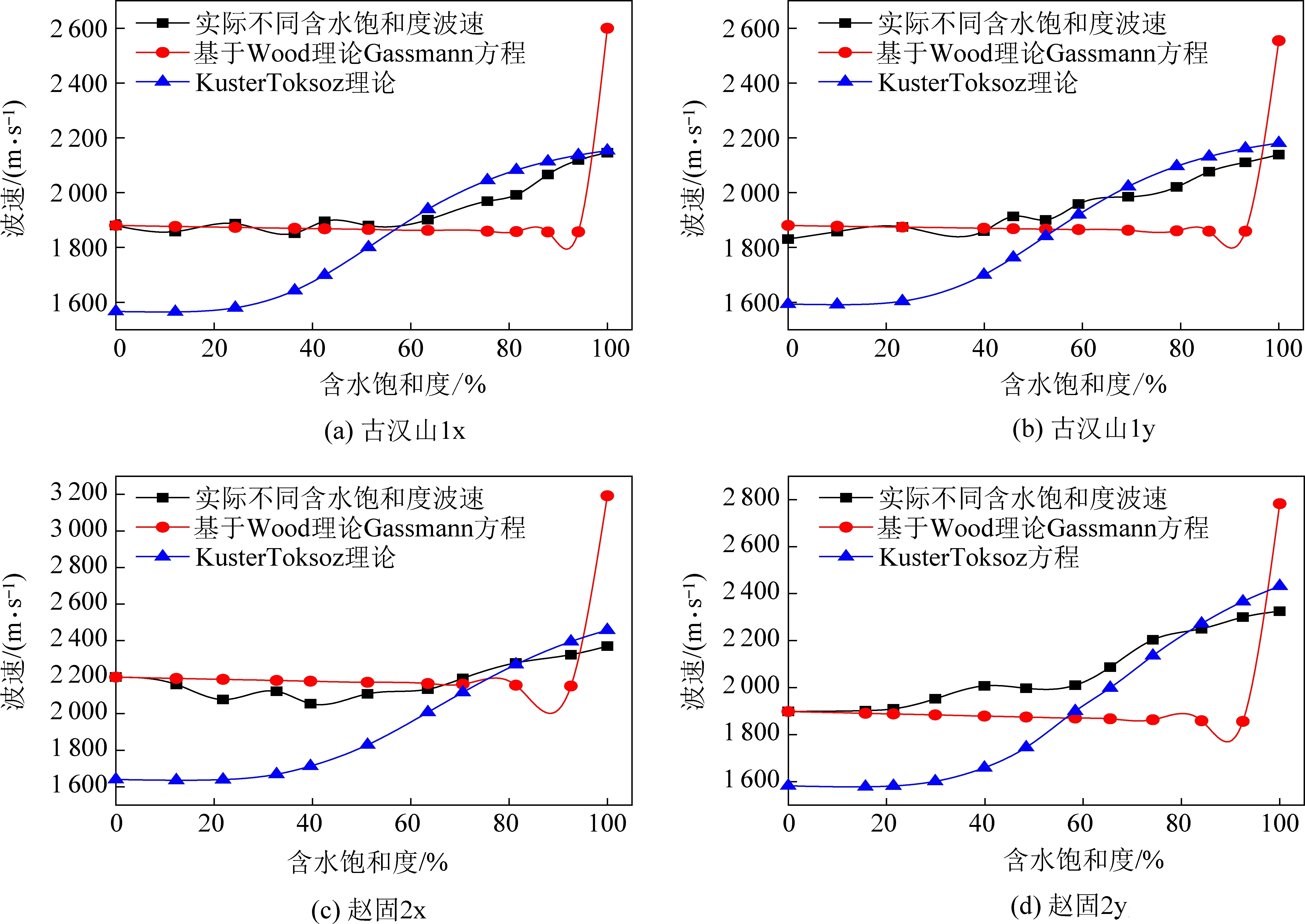
图2 不同煤样实际含水饱和度与不同模型含水饱和度对比Fig.2 Comparison between actual water saturation of different coal samples and water saturation of different models

而垂直层理煤样孔隙发育高，孔隙率较大。当煤样浸水时，水快速进入煤样，使原来煤样中空气减少，而波在水中传播速度远大于空气，使得波速在煤样中传播缩短了传播路径，同时反射、散射等现象降低，从而导致波速上升。同样水的进入也会使煤体软化，阻碍波速的传播。在含水饱和度60%之前，水导致波速加快速度大于水使煤体软化波速降低的速度，导致波速增大，且成缓慢增加。不符合Wood理论假设的Gassmann方程。

当样品的含水饱和度在60%～100%时，无论烟煤还是无烟煤平行层理还是垂直层理波速明显上升。查阅相关文献，此阶段符合Kuster-Toksoz[18]理论。该理论利用弹性波散射理论，将双相介质等效为一种连续介质，使得入射波通过等效介质产生的位移场和由入射波经每个孔隙散射引起的位移场相同，用长波一阶散射理论推导了对多种包含物形状的等效模量的Kuster-Toksoz表达式，其推广后的形式可以写成如下所示：

(12)

(13)

其中：

(14)

(15)

(16)

(17)

(18)

(19)

(20)

F6=1+A[1+g-R(g+φ)]+B(1-φ)(3-4R)

(21)

(22)

(23)

F9=A[g(R-1)-Rφ]+Bφ(3-4R)

(24)

(25)

(26)

(27)

(28)

(29)

式中：Tijij和Tiijj为对称能四阶张量，取决于包含物形状；K*为推导后的等效体积模量；μ*为推导后的等效剪切模量；K为体积模量；μ为切变模量；K′为孔隙的体积模量；μ′为孔隙的切变模量；α为孔隙纵横比；c为孔隙体积；g与φ均为中间变量。

通过Kuster-Toksoz理论计算，如图2中蓝色线所示，不管垂直层理还是平行层理含水饱和度在60%～100%时，Kuster-Toksoz模型计算的波速是增加的，与实际波速(黑色线)走势大小基本吻合。所以此阶段符合Kauster-Toksoz理论。

60%～100%阶段波速明显上升，是由于波速在水中传播速度大于空气，水分逐步充满煤样孔隙，水代替空气而成为孔隙中连同的液相，裂隙状的小孔开始被饱和。导致裂隙状孔刚度增加，使得波速在煤样中传播缩短了传播路径，同时反射、散射等现象降低，从而导致波速上升。

垂直层理煤样含饱和度在60%之前，由于孔、裂隙较发育，水的进入作用大于水使煤样软化的作用，导致纵波波速缓慢上升。结合分析与试验现象，把垂直层理含水饱和度在60%之前，进行波速与不同含水饱和度变化规律定量分析，进过计算分析得出垂直层理含水饱和度在60%之前符合以下修正公式：

(30)

其中：Srt为煤样第1次转折是(第2阶段快速增加的起点)的含水饱和度；Sr为Srt之前煤样不同含水饱和度；v0为煤样干燥时的波速；vrt为煤样在Srt饱和度下的波速。通过计算与实际波速相比较，得如结论如图3所示。

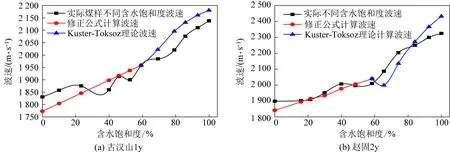
图3 不同煤样实际含水饱和度与修正公式、模型含水饱和度对比Fig.3 Comparison between actual water saturation of different coal samples and water saturation of modified formula and model

分析得出：无论烟煤还是无烟煤煤样含水饱和度在60%之前，修正公式计算的波速(红色线)与实际波速走势基本吻合，波速大小相差不大。含水饱和度60%之后，Kauster-Toksoz理论计算波速与实际波速走势、大小基本吻合，符合Kauster-Toksoz理论。

3 结 论

1)赵固无烟煤平行层理与垂直层理波速大于古汉山烟煤平行层理与垂直层理波速，且无论赵固无烟煤还是古汉山烟煤，干燥时平行层理波速大于垂直层理波速。

2)无论是烟煤还是无烟煤平行层理煤样在含水饱和度60%之前，波速随不同含水饱和度增加而下降，在含水饱和度60%之后波速快速上升。而垂直层理煤样在含水饱和度60%之前，波速随不同含水饱和度增加而缓慢增加，在含水饱和度60%之后波速快速上升。

3)平行层理煤样在含水饱和度60%波速与Wood理论假设的Gassmann方程计算波速基本吻合，在含水饱和度60%之后波速与Kauster-Toksoz理论计算波速基本吻合。垂直层理煤样在含水饱和度60%波速与修正公式计算波速基本吻合，在含水饱和度60%之后波速与Kauster-Toksoz理论计算波速基本吻合。