煤矿高强度长壁开采覆岩破坏充分采动及其判据
2020-12-17郭文兵赵高博白二虎
郭文兵,赵高博,白二虎
(1.河南理工大学 能源科学与工程学院,河南 焦作 454000; 2.煤炭安全生产河南省协同创新中心,河南 焦作 454000)
煤矿开采是一次对矿区地层的扰动,必然引起上覆岩层的破坏和应力场与裂隙场的改变,其中引起的覆岩破坏高度(也称“导水裂隙带高度”,即垮落带与裂缝带高度的总和)对水体下采煤、保水开采、瓦斯治理的解放层开采等均具有重要意义[1-3]。
钱鸣高等[4]提出的关键层理论对采场上覆岩层活动及其结构形态提供了一种重要的思想和方法;许家林等[5-6]在此基础上结合工程探测的方法,研究了关键层位置对覆岩破坏高度的影响,并提出了一种基于关键层位置预计覆岩破坏高度的方法;郭文兵等[7-8]研究了覆岩破坏传递的过程,并将覆岩破坏划分为两个阶段:覆岩破坏非充分采动阶段和覆岩破坏充分采动,基于此提出了一种基于覆岩破坏传递的覆岩破坏高度预计方法;高延法等[9-10]研究了覆岩裂缝与岩层拉伸变形之间的关系,并提出了一种考虑覆岩组合结构与岩层拉伸变形的覆岩破坏高度预计方法。
上述研究针对预计覆岩破坏高度的方法取得了较大的进展,但关于如何控制覆岩破坏高度的研究较少。其中关于近水体下安全采煤的技术措施之一是:缩短工作面开采尺寸[11],但具体将工作面尺寸缩短为多少时可以控制覆岩破坏高度尚不明确。
因此,笔者基于覆岩破坏充分采动的定义,分析了其特征及影响因素,采用理论分析、数值模拟,研究给出了高强度开采覆岩破坏充分采动的判据。
1 覆岩破坏充分采动特征及影响因素
根据文献[8],覆岩破坏充分程度可划分为:覆岩破坏非充分采动和覆岩破坏充分采动,并将覆岩破坏充分采动定义为某一工作面开采引起的覆岩破坏高度达到其采矿地质条件下的最大值,且随开采尺寸的增加,其高度不再增加的阶段。
为分析覆岩破坏非充分采动与充分采动的特征及影响覆岩破坏充分采动的因素,给出了覆岩破坏过程及覆岩破坏非充分采动、充分采动的示意图(图1)。
由图1可知,当工作面推进距离为LS1时,仅形成垮落带(图1(a));随着推进距离的增加覆岩破坏向上发育,裂缝带形成(图1(b)),且与未破坏岩层之间存在较大的离层裂缝(空间);若推进距离继续增加,覆岩破坏高度增加且离层裂缝(空间)减小,这处于覆岩破坏非充分采动阶段。
当推进距离为L′S,裂缝带的岩块与弯曲下沉带的岩层将存在点与面、线与面以及面与面的接触且相互作用,这时离层将趋于闭合,覆岩破坏高度发育到最大值,达到覆岩破坏充分采动。因此,覆岩破坏充分采动的特征为:① 裂缝带与弯曲下沉带之间的离层裂缝趋于闭合;② 覆岩破坏高度随着推进距离的增加不再增加;③ 覆岩破坏高度达到最大值。
基于上述分析可知,直接影响覆岩破坏充分采动的因素主要有推进距离(LS)、离层高度(Δ)、以及覆岩破坏最大高度(Hmax)。另外,离层高度与开采厚度(M)、各岩层厚度(hi)、覆岩碎胀系数(K)有关[12-13];《建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规范》中计算覆岩破坏高度的经验公式表明其与采煤方法、覆岩岩性及开采厚度有关[15];根据文献[8]提出的临界工作面倾向长度公式及文献[16]可知,覆岩充分采动的影响因素有开采尺寸、开采厚度、开采深度、覆岩岩性。因此,综合分析可知影响覆岩破坏充分采动的因素主要有工作面开采尺寸(走向、倾向长度)、开采厚度、开采深度、覆岩岩性。
2 覆岩破坏充分采动理论
为定性分析上述因素对覆岩破坏充分采动的影响,从二维平面及三维空间的角度对覆岩破坏充分采动进行理论分析。
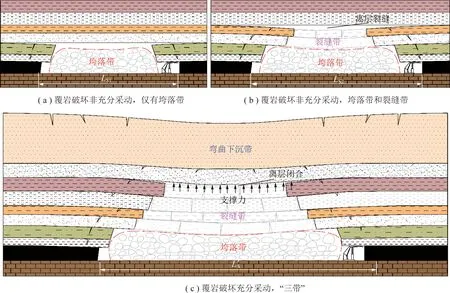
图1 覆岩破坏过程及覆岩破坏非充分采动、充分采动Fig.1 Overburden failure process and overburden failure of subcritical and critical
2.1 二维覆岩破坏充分采动理论
覆岩破坏主要是由于工作面推进距离增加引起的,且覆岩运移最终传递至地表形成下沉盆地。简言之,二维平面下采空区面积的增加引起了覆岩破坏面积与地表下沉面积的增加。根据覆岩破坏传递的过程[7],覆岩破坏后的形态由于覆岩岩层悬伸距的存在将呈现为“梯形”,基于此将覆岩预破坏面积简化为梯形的面积(与工作面推进距离、覆岩破断角及覆岩破坏高度有关),采空区面积简化为矩形的面积(与工作面推进距离和开采厚度),如图2所示。
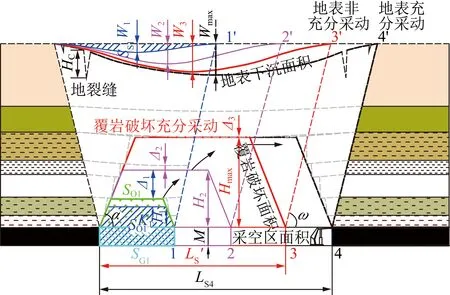
图2 二维覆岩破坏充分采动“梯形-面积”分析示意Fig.2 Overburden critical failure analysis based on the area of trapezoid from two-dimensional perspective
由图2可知,工作面推进至位置1时,采空区矩形面积为SG1,上覆岩层预破坏梯形面积为SO1,覆岩破坏后的面积由于破坏岩层碎胀系数增长至SO1K1,且地表下沉面积为SS1,这时覆岩破坏高度为H1,失稳岩层与未失稳岩层的离层高度为Δ1,地表下沉值为W1。当工作面推进至位置2时,覆岩破坏高度增大至H2,离层高度减小为Δ2,地表下沉值为W2。工作面推进至位置1和位置2时均处于覆岩破坏非充分采动,采空区矩形面积(SG)与上覆岩层预破坏梯形面积(SO)的总和>覆岩破坏后的面积(SOK)与地表下沉面积的总和(SS),即
SG+SO>SOK+SS
(1)
式中,K为覆岩破坏后的碎胀系数。
当工作面推进至位置3时,覆岩破坏发育至最大高度,达到覆岩破坏充分采动阶段,即:理论上失稳岩层与未失稳岩层的离层高度减小至Δ3=0,且采空区矩形面积与上覆岩层预破坏梯形面积被覆岩破坏后的面积与地表下沉面积完全替换。这时,采空区矩形面积、上覆岩层预破坏梯形面积、上覆岩层破坏后的面积、地表下沉面积的关系为
SG+SO=SOK+SS
(2)
SG=MLS
(3)

(4)

(5)
式中,Hi为工作面推进至位置i时的覆岩破坏高度,m;α为覆岩破断角均值,(°);r为主要影响半径,为开采深度(H)与主要影响角正切(tanβ)的比值,m;W(x)为走向主断面内的半无限开采地表下沉曲线公式。
联合式(2)~(5)可得
式中,L′S为二维平面覆岩破坏充分采动时的工作面推进距离,m。
解式(6)得
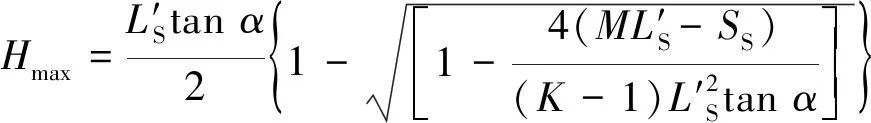
(7)
因此,得到了二维平面下覆岩破坏充分采动时覆岩破坏最大高度(Hmax)的理论计算公式。
当工作面推进至位置3时,虽然覆岩破坏处于充分采动阶段(覆岩破坏高度达到最大),但失稳垮落岩块间的空隙、空间比较发育,失稳岩层间的离层裂缝仍未完全闭合,覆岩弯曲变形尚未完全传递至地表,因此,此时的地表下沉值为W3,尚未达到最大,处于地表非充分采动阶段。当工作面推进至位置4时,覆岩破坏高度不再增加,处于覆岩破坏超充分阶段,这时地表下沉值将达到最大值Wmax,进入地表充分采动阶段。
另外,根据上述分析,可得到覆岩“两带”破坏模式(垮落带和裂缝带)的判别式为
Hmax+HC+Wmax>H
(8)
式中,HC为地表裂缝的深度,m;Wmax为地表下沉最大值,m。
2.2 三维覆岩破坏充分采动理论
现场实际工作面的回采处于三维的空间,为进一步分析现场的覆岩破坏充分采动,将上述二维平面覆岩破坏“梯形-面积”转化为三维空间覆岩破坏,则需要考虑工作面倾向长度(LD),如图3所示。
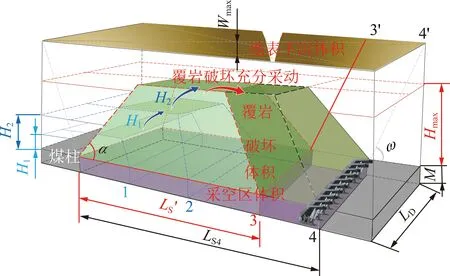
图3 三维覆岩破坏充分采动“四棱台-体积”分析示意Fig.3 Overburden critical failure analysis based on the volume of four prism from three-dimensional perspective
与上述二维平面覆岩破坏理论分析类似,将“梯形-面积”转化为“四棱台-体积”,因此当覆岩破坏处于非充分采动,有
VG+VO>VOK+VS
(9)
式中,VG为采空区长方体体积,m3;VO为上覆岩层预破坏四棱台体积,m3;VS为地表下沉体积,m3。
当达到覆岩破坏充分采动时,有
VG+VO=VOK+VS
(10)
其中,
VG=MLSLD
(11)

(12)
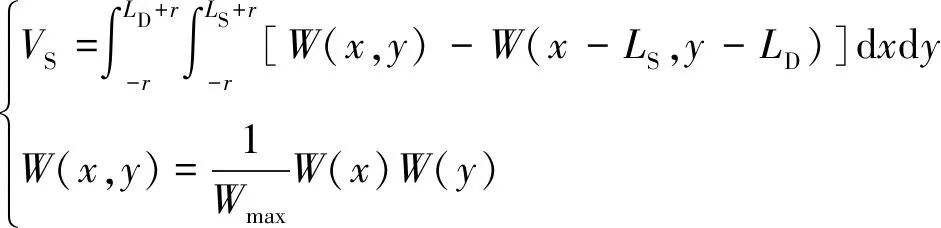
(13)
式中,W(y)为倾向主断面内的半无限开采地表下沉曲线公式[10]。
联合式(10)~(13)得

(14)
式中,L′S为三维空间覆岩破坏充分采动时的工作面推进距离,m。
解式(14)得

(15)
因此,得到三维空间下覆岩破坏充分采动时覆岩破坏高度(Hmax)理论计算公式。
综合式(7),(15)可知,覆岩破坏充分采动时的覆岩破坏最大高度与开采厚度、开采尺寸、开采深度、覆岩破坏后的碎胀系数以及覆岩破断角有关,且与开采厚度、工作面推进距离、覆岩破断角成正相关关系,与覆岩破坏后的碎胀系数、地表下沉面积、体积成负相关关系。
根据上述分析,创新性的将长壁开采三维覆岩破坏及地表下沉简化为4类采动影响体积(采空区长方体体积、上覆岩层预破坏四棱台体积、覆岩破坏后的体积与地表下沉体积)之间的关系,较为直观的体现了长壁开采导致的覆岩破坏与地表下沉,并将采动覆岩破坏与地表沉陷的准静态建立了联系。
3 覆岩破坏充分采动数值模拟
根据上述覆岩破坏充分采动理论分析,得到了二维平面及三维空间下覆岩破坏充分采动时覆岩破坏高度理论表达式,可用于定性分析各个影响因素之间的关系,但因其形式复杂,现场应用困难,因此有必要对覆岩破坏充分采动进行数值模拟分析。
3.1 数值模拟方案
3.1.1高强度开采工作面概况
选取神东沙吉海煤矿B1003W01工作面为研究对象,该工作面平均采深约280 m,走向长度1 930 m,工作面倾斜宽度210 m,推进速度为5.8 m/d,煤层倾角平均13°,开采厚度平均为6.5 m,综合机械化放顶煤开采,符合高强度开采工作面的定义及特征[17-18]。根据实测资料[19],该矿最大水平主应力与最小水平主应力的比值介于1.79~1.91,平均1.85;最大水平主应力与垂直应力的比值介于1.47~1.54,平均1.50。根据地应力测量,沙吉海煤矿最大水平主应力与工作面推进方向的夹角<20°,取18°,工作面上覆岩层岩性属于软弱。综合相关钻孔,工作面上覆岩层180 m范围内的覆岩柱状如图4所示。
3.1.2数值模拟方案及模型建立
根据上述分析的覆岩破坏充分采动影响因素,借助3DEC离散元数值模拟软件分别模拟开采不同厚度(3.5,6.5,9.5,12.5,15.5 m)、不同倾向长度(180,210,240,270,300 m)、不同开采深度(180,280,380,480,580 m)时覆岩达到充分采动程度的工作面推进距离。
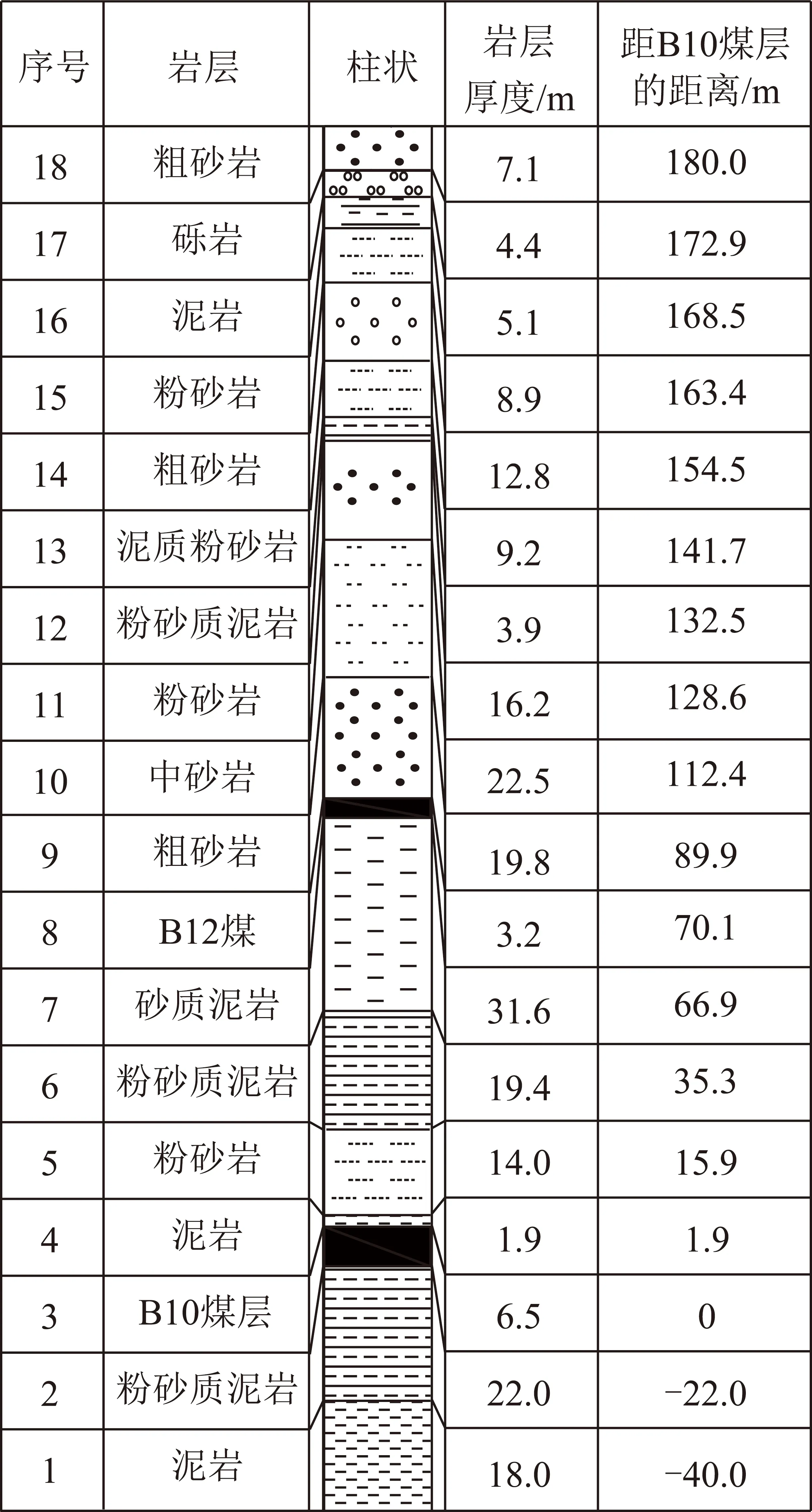
图4 覆岩柱状Fig.4 Overburden strata structure
另外,如图5所示,模拟沙吉海煤矿B1003W01高强度开采工作面与最大主应力的夹角为18°,走向长度为300 m,每15 m开挖1次,共开挖20步。为去除边界效应,边界煤柱为100~193 m。模拟工作面上覆岩层范围为180 m,并在模型上方施加未模拟的100 m岩层载荷2.5 MPa;工作面底板岩层总厚度为40 m。三维数值模型尺寸为:550 m×511 m×226.5 m(长×宽×高)。
3.1.3数值模拟模型校核基于沙吉海B1003W01高强度开采工作面原采矿地质条件,考虑最大、最小水平主应力的比值、最大水平主应力与竖直应力的比值,模拟开采厚度6.5 m,工作面倾向长度210 m,开采深度280 m时的覆岩破坏情况,并对模型进行校核,其中覆岩各岩层及其节理的模拟力学参数见表1。
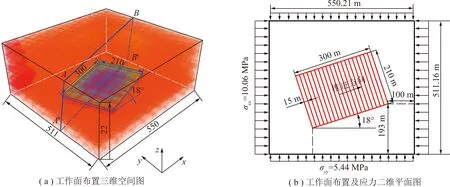
图5 数值模拟模型尺寸及工作面布置Fig.5 Size of numerical simulation model and panel layout
以节理法向位移判断覆岩裂隙发育情况,进而得到覆岩破坏高度,沙吉海B1003W01工作面部分覆岩破坏高度发育过程中的节理法向位移图如图6所示。
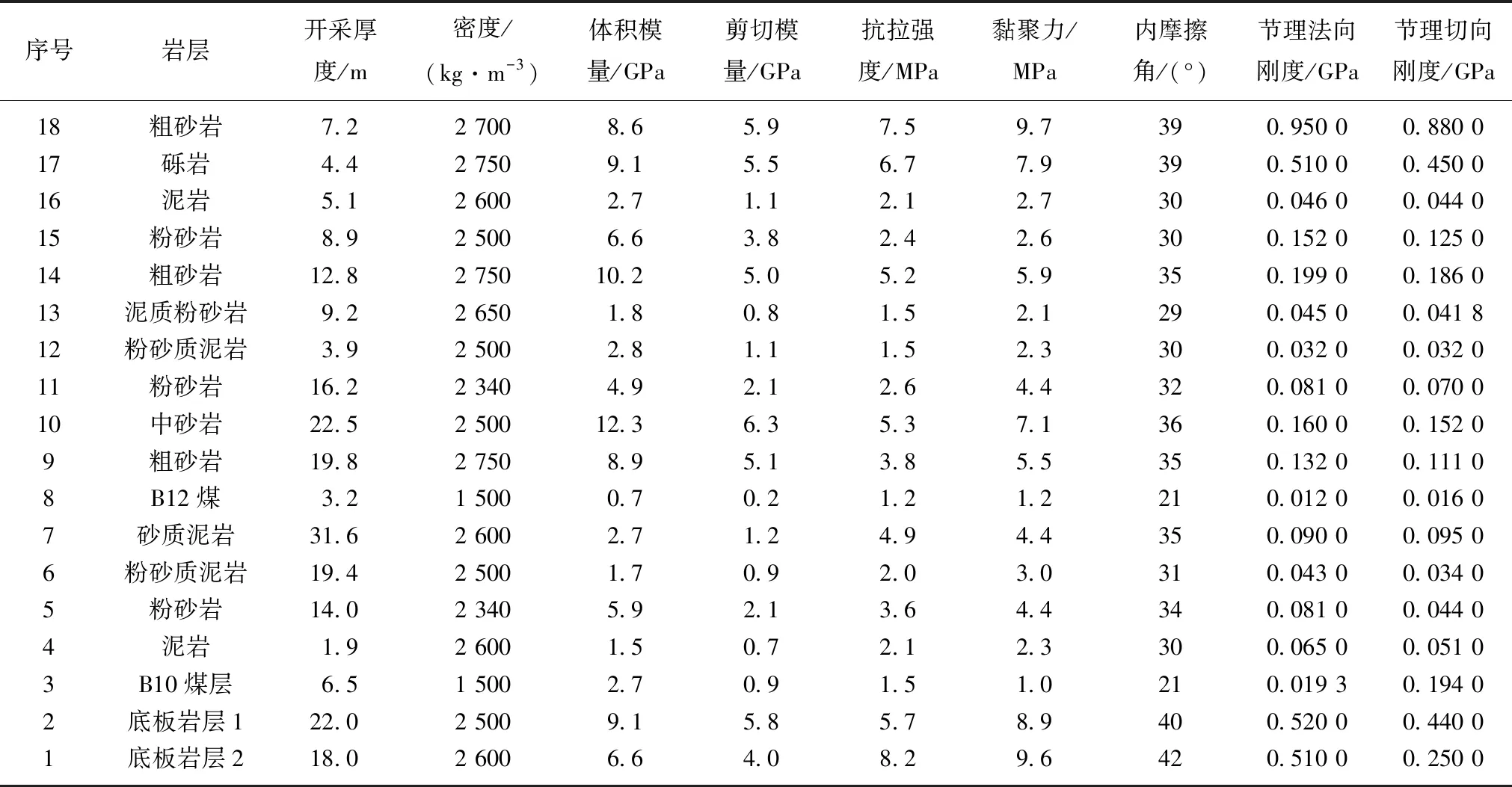
表1 覆岩各岩层及节理模拟力学参数Table 1 Parameters of mining strata and block contact face
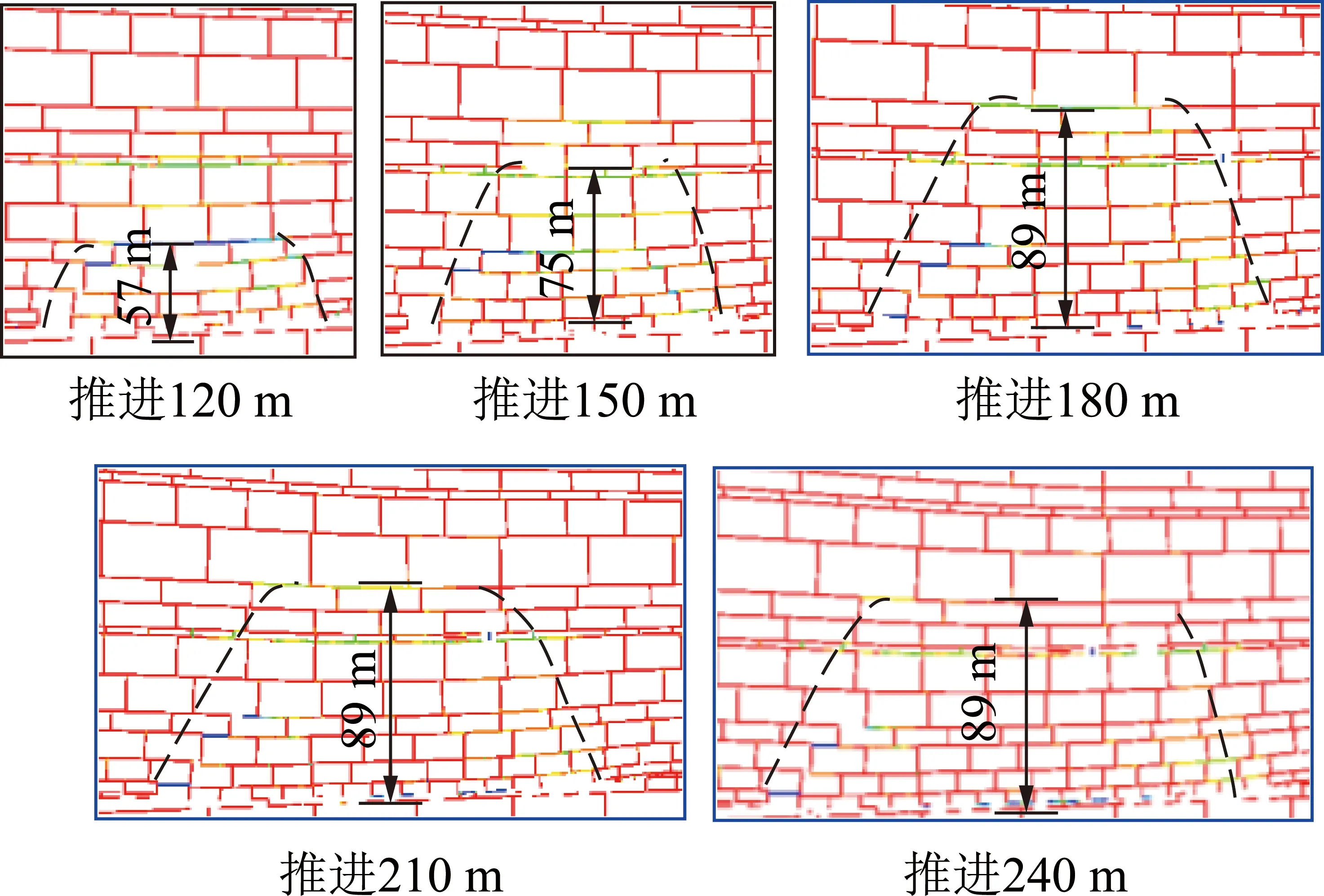
图6 沙吉海B1003W01工作面覆岩破坏法向节理位移Fig.6 Joint normal displacement of overburden failure of No.B1003W01 panel in shajihai coal mine
由图6可知,当工作面推进至180 m时覆岩破坏最大高度为89 m,达到覆岩破坏充分采动,其覆岩破坏发育过程及三维覆岩破坏充分采动节理法向位移图如图7,8所示。
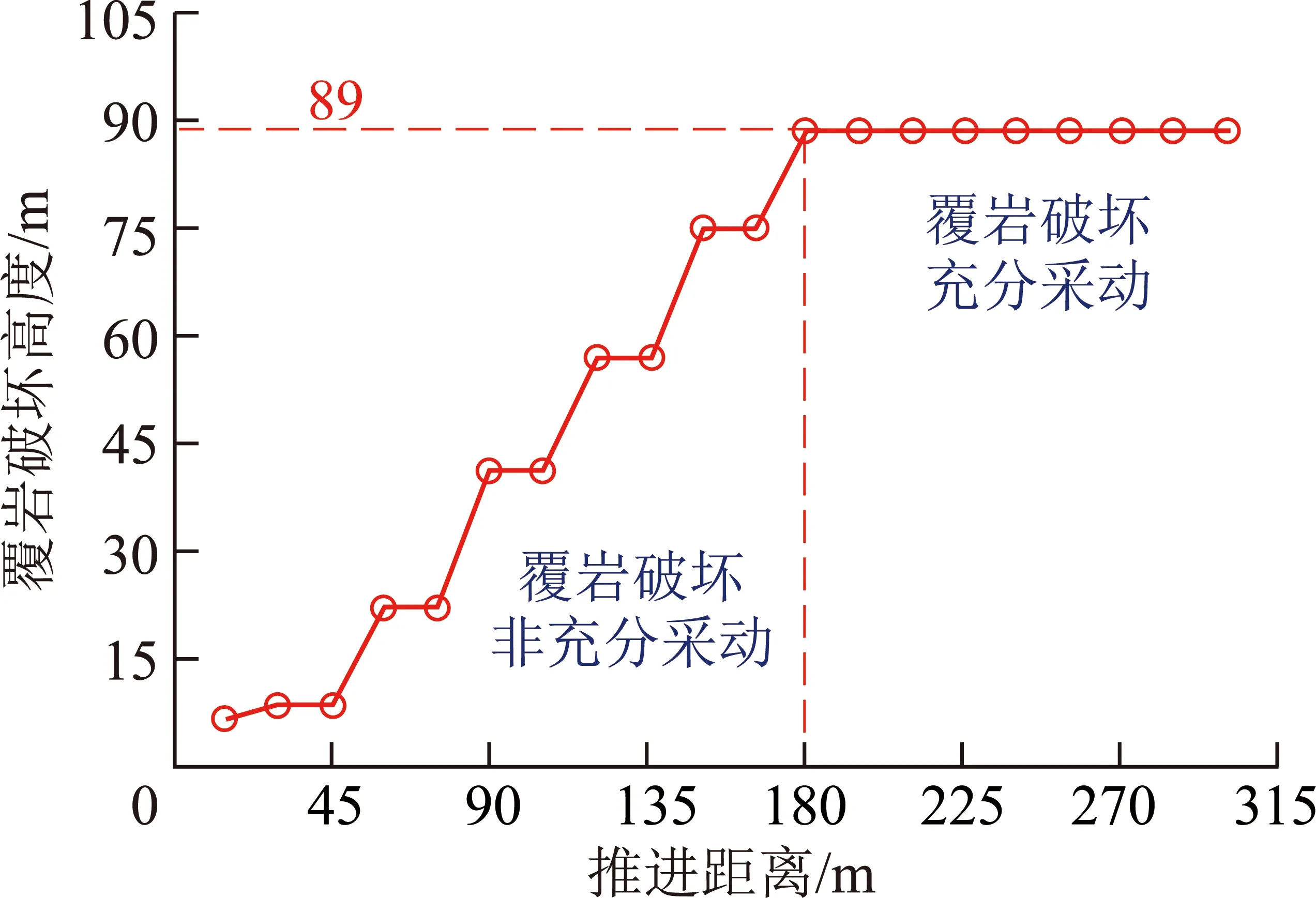
图7 沙吉海B1003W01工作面覆岩破坏高度发育曲线Fig.7 Curve of overburden failure of No.B1003W01 panel in shajihai coal mine
由数值模拟可知,覆岩破坏最大高度(89 m)和初次来压步距(30 m)与现场实测的76~82 m,28~35 m相近[20],数值模拟模型合理,可用于不同开采厚度、倾向长度及深度的数值模拟分析。
3.2 数值模拟结果
3.2.1不同开采厚度对覆岩破坏充分采动的影响
不同开采厚度的覆岩破坏高度发育过程及达到覆岩破坏充分采动时的推进距离曲线如图9所示。
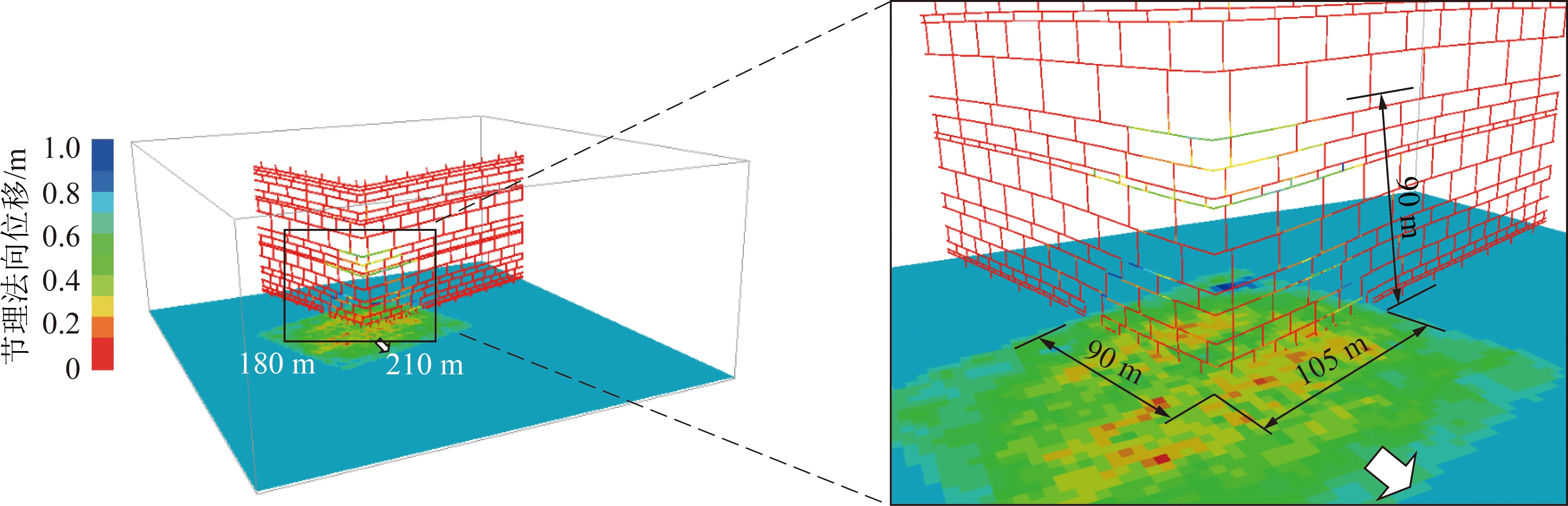
图8 沙吉海B1003W01工作面覆岩破坏充分采动时的三维节理法向位移Fig.8 Joint normal displacement of overburden critical failure of No.B1003W01 panel from 3D perspective
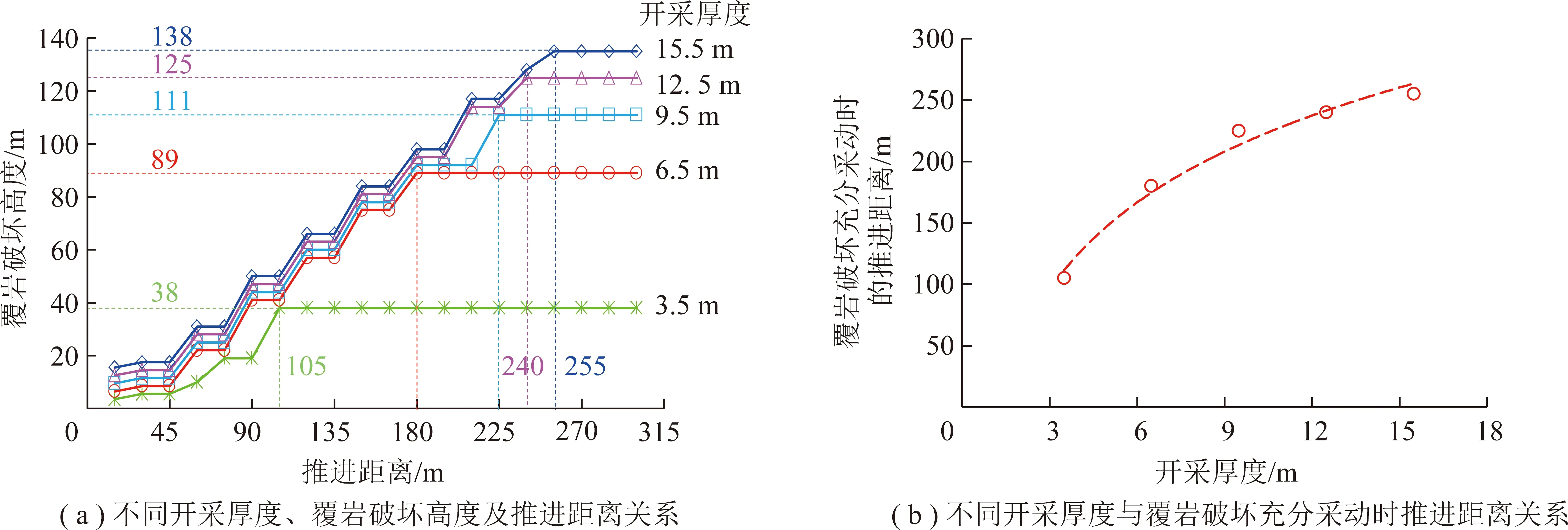
图9 开采厚度对覆岩破坏充分采动的影响分析Fig.9 Influence of the mining height on overburden critical failure in shajihai coal mine
由图9可知,开采厚度越大,覆岩破坏达到充分采动的推进距离越大。开采厚度(M)与覆岩破坏充分采动时的推进距离(L′S)关系式为
L′S=102.1lnM-16.324,R2=0.981
(16)
3.2.2不同倾向长度对覆岩破坏充分采动的影响
不同倾向长度的覆岩破坏高度发育过程及达到覆岩破坏充分采动时的推进距离曲线如图10所示。
由图10可知,倾向长度越大,覆岩破坏达到充分采动的推进距离越小。倾向长度(LD)与覆岩破坏充分采动时的推进距离(L′S)关系式为
L′S=-0.5LD+285,R2=1
(17)
3.2.3不同开采深度对覆岩破坏充分采动的影响
不同开采深度的覆岩破坏高度发育过程及达到覆岩破坏充分采动时的推进距离曲线如图11所示。
由图11可知,开采深度越大,覆岩破坏达到充分采动的推进距离越小。开采深度(H)与覆岩破坏充分采动时的推进距离(L′S)关系式为
L′S=-0.27H+246.6,R2=0.976
(18)
根据上述分析可知,覆岩破坏充分采动时的推进距离与开采厚度成正相关,与倾向长度、开采深度成负相关。
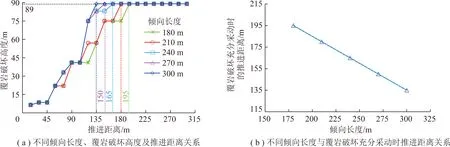
图10 倾向长度对覆岩破坏充分采动的影响分析Fig.10 Influence of the panel dip length on overburden critical failure
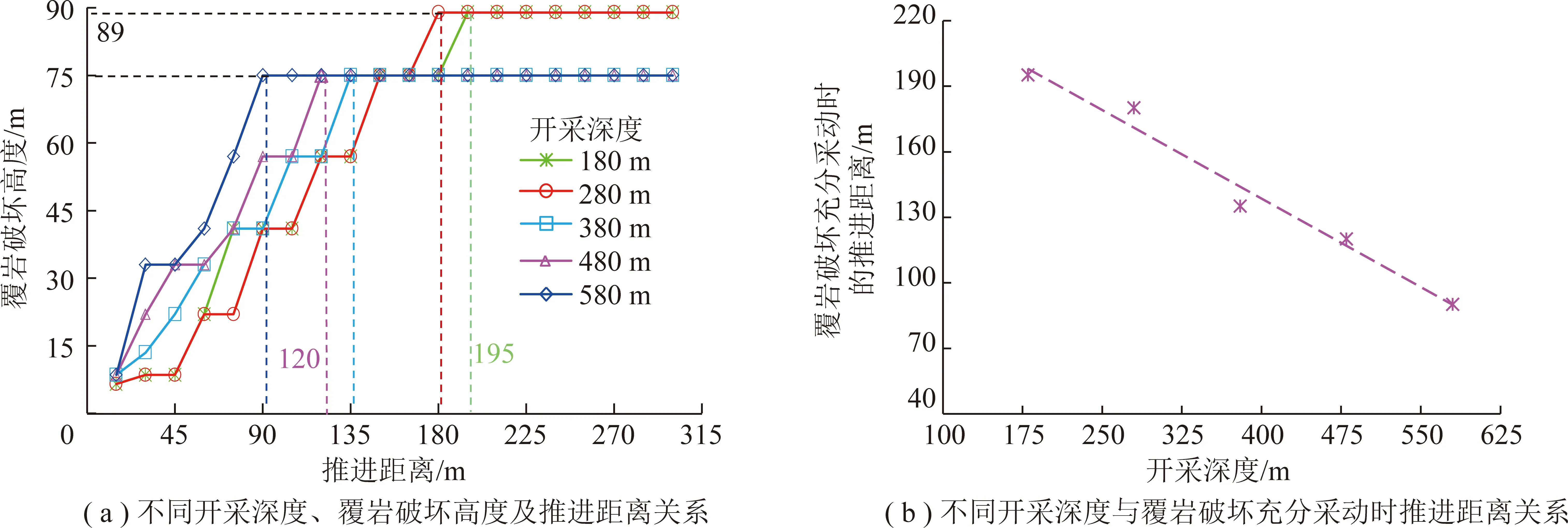
图11 开采深度对覆岩破坏充分采动的影响分析Fig.11 Influence of the mining depth on overburden critical failure
另外,就沙吉海矿地质采矿条件而言,通过上述数值模拟结果分析可得:
(1)覆岩破坏高度随高强度开采工作面推进距离的增加而增加,且与开采厚度成明显的正相关关系(图9),与上述式(7),(15)的覆岩破坏最大高度公式理论分析结果相吻合。
(2)当高强度开采工作面的倾向长度大于180 m时,覆岩破坏高度不再随工作面倾向长度的增加而增加(图10)。
(3)覆岩破坏高度与开采深度(180~580 m)成一定的负相关关系。
4 高强度开采覆岩破坏充分采动判据
4.1 覆岩破坏充分采动模拟结果
为进一步分析高强度开采覆岩破坏充分采动,对数值模拟结果进行汇总,见表2。

表2 中硬或软弱覆岩破坏充分采动模拟结果汇总Table 2 Summary of simulation results of overburden critical failure m
据表2,深厚比(H/M)与覆岩破坏充分采动时的推进距离(L′S)的关系曲线如图12所示。由图12可知,深厚比与覆岩破坏达到充分采动的推进距离成负相关,关系式为

(18)
4.2 高强度开采覆岩破坏充分采动判据
根据上述分析,覆岩破坏充分采动时推进距离(L′S)与工作面倾向长度(LD)、深厚比(H/M)成反比。综合分析得到工作面倾向长度与深厚比的乘积对覆岩破坏充分采动时推进距离的影响曲线,如图13所示。

图12 深厚比与覆岩破坏充分采动时的推进距离的关系Fig.12 Ratio of mining depth and mining height vs.advanced distance at overburden critical failure stage

图13 倾向长度与深厚比的乘积与覆岩破坏充分采动时的推进距离的关系Fig.13 Product of dip length and ratio of mining depth and mining height vs.advanced distance at overburden critical failure stage
由图13得到高强度开采工作面覆岩破坏充分采动的判定公式:
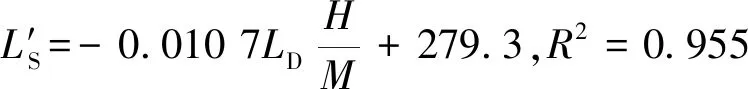
(19)
式中,覆岩岩性为中硬或软弱;开采厚度为3.5~15.5 m;倾向长度为180~300 m;开采深度为180~580 m。
4.3 工程实例验证
选取了8个高强度开采工作面,应用式(19)进行核算,验证判据公式的合理性,计算结果见表3。
根据上述结果,得到高强度开采工作面达到覆岩破坏充分时推进距离均小于其开采深度,说明覆岩破坏达到充分采动提前于地表达到充分采动(需要达到1.2H~1.4H)。另外,根据高强度开采覆岩破坏充分采动判据,将工作面推进距离缩短至小于临界推进距离时可控制覆岩破坏高度。
另外,目前覆岩破坏高度现场实测数据较多,但这些实测结果尚不能确定其是否在覆岩破坏充分采动阶段测得的最大值,根据本文提出的覆岩破坏充分采动判据式(19),可计算得到高强度开采工作面达到覆岩破坏充分采动时所需的推进距离,当高强度开采工作面推进距离满足覆岩破坏充分采动时,可在现场实测出覆岩破坏最大高度。
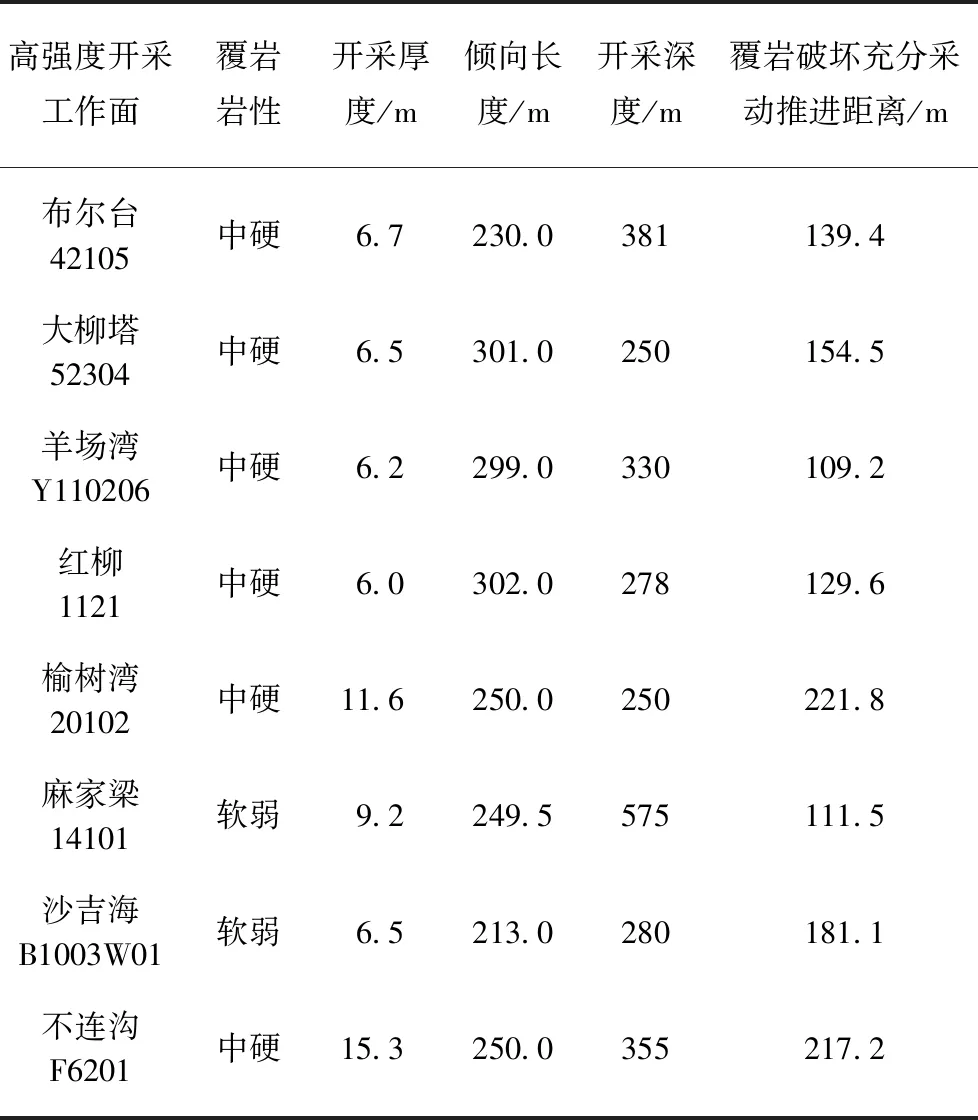
表3 高强度开采工作面覆岩破坏充分采动推进距离Table 3 Advanced distances at overburden critical failure stage with some high-intensity mining panel
5 结 论
(1)分析了覆岩破坏充分采动的特征及其影响因素,提出了一种覆岩破坏充分采动的理论判别方法,将长壁开采三维覆岩破坏及地表下沉简化为4类采动影响体积之间的关系,得出了覆岩破坏充分采动时覆岩破坏高度理论表达式与覆岩“两带”破坏模式的判别式。
(2)以某高强度开采工作面为原型,建立并校核了考虑现场最大、最小水平主应力方向与工作面推进方向夹角的三维数值模型,通过数值模拟分析了不同开采厚度、开采尺寸及开采深度对高强度开采覆岩破坏充分采动的影响。结果表明:工作面达到覆岩破坏充分采动时的推进距离与工作面倾向长度、深厚比成反比。
(3)研究给出了高强度开采覆岩破坏充分采动的判据及其适用条件,并进行了工程实例验证。
