考虑弹性模量退化的砂岩非定常蠕变模型

2022-07-20孙博一孙艺丹晏祥智

煤炭科学技术 2022年5期

杨逾，孙博一，孙艺丹，李珉，晏祥智

(1.辽宁工程技术大学土木工程学院，辽宁阜新 123000；2.云南省房地产开发经营有限公司，云南昆明 650000)

0 引言

岩石的流变性指的是在外力、温度、辐射等条件下，岩石的力学参数和结构呈现出与时间相关的特性变化，包括蠕变、长期强度、应力松弛等[1-3]。目前，岩石流变研究大多基于元件理论，即通过基本流变元件(虎克体、圣维南体、牛顿黏壶)的不同串并联组合模型，合理且有效的描述了许多岩石的蠕变规律，其中应用最为广泛的是西原模型。但西原模型仅能描述岩石蠕变过程中的衰减蠕变和稳定蠕变，对于加速蠕变阶段的特性研究难以实现。笔者旨在研究蠕变曲线进入加速蠕变状态的应力阈值以及对加速蠕变阶段的模型公式进行推导反演。

对于加速蠕变阶段的研究，目前常用的方法有2种[4]：① 采用新的非线性元件代替常规的线性牛顿体，有效地描述了岩石蠕变过程中的非线性变形特征，为研究岩石的非线性流变问题提供了新的思路；② 引入不同的理论，如损伤力学理论、应变能理论、分数阶理论等，更加真实有效的反映出岩石的蠕变机制。其中前者通过引入非线性元件建立岩石加速蠕变阶段的非线性模型，比如邓荣贵等[5]、徐卫亚等[6]提出了一个新的非线性黏滞元件，对黏性元件的本构关系进行改进以模拟加速蠕变曲线，康永刚等[7]基于非牛顿流体的幂律函数形式提出了修正凯尔文体模型，韩阳等[8]提出了一种非线性黏壶元件来改进Burgers模型，并将非定常Burgers模型的蠕变方程推广至三维应力状态。其中后者通过引入不同理论建立非线性蠕变模型，何志磊等[9]基于分数阶理论，在考虑参数非定常特性的基础上，建立可以克服传统西原体难以描述加速蠕变的非线性模型；刘开云等[10]考虑弹性模量随时间的弱化规律，引入一个非线性黏塑性体，建立非定常非线性模型。张强勇等[11]基于损伤力学理论，提出了弹性模量和黏滞系数的损伤演化方程，建立了变参数蠕变损伤本构模型。

采用方法②，基于西原模型，引入损伤变量，对弹性模量、黏滞系数进行非定常变参，且将岩石的长期强度作为损伤应力阈值[12-13]，据此建立以屈服强度σs和长期强度σ∞为判别条件的三段式非定常蠕变模型方程表达式，并将一维本构模型推广到三维本构模型，使之更加符合工程实际状况。并采用该流变模型对辽宁阜新海棠山隧道砂岩流变试验全过程曲线进行模型参数反演，通过与试验结果的对比分析，改进的模型不仅反映出砂岩瞬时应变、稳定蠕变和亚稳定蠕变阶段的流变特性，还能很好地描述了砂岩加速蠕变阶段的流变特性，同时也验证了以屈服强度σs和长期强度σ∞为判别条件的合理性。最后，根据模型参数反演的结果建立砂岩流变参数的损伤演化方程，为岩体流变的非线性问题提供了一个研究思路。

1 砂岩三轴蠕变试验

砂岩试样取自辽宁阜新海棠山隧道，首先进行切割、取样、打磨，根据《岩石试验方法标准》(GB 50218—1994)，制成直径50 mm、高度100 mm的圆柱状试样，选取符合上述规范精度要求的试样24个，其中12个进行三轴压缩试验，剩余12个进行三轴蠕变试验。

首先进行三轴压缩试验，三轴压缩试验是三轴蠕变试验的基础，通过三轴压缩试验测定不同围压下砂岩的峰值强度，以此确定三轴蠕变试验的各级应力水平。取12个试样分成4组，每组3个，使用MTS812.02岩石试验系统，如图1所示，分别进行围压5、10、15、20 MPa的砂岩三轴压缩试验。试验数据由试验机自动采集并输入到数据采集系统，采集间隔为2 s，将试验结果整理见表1。

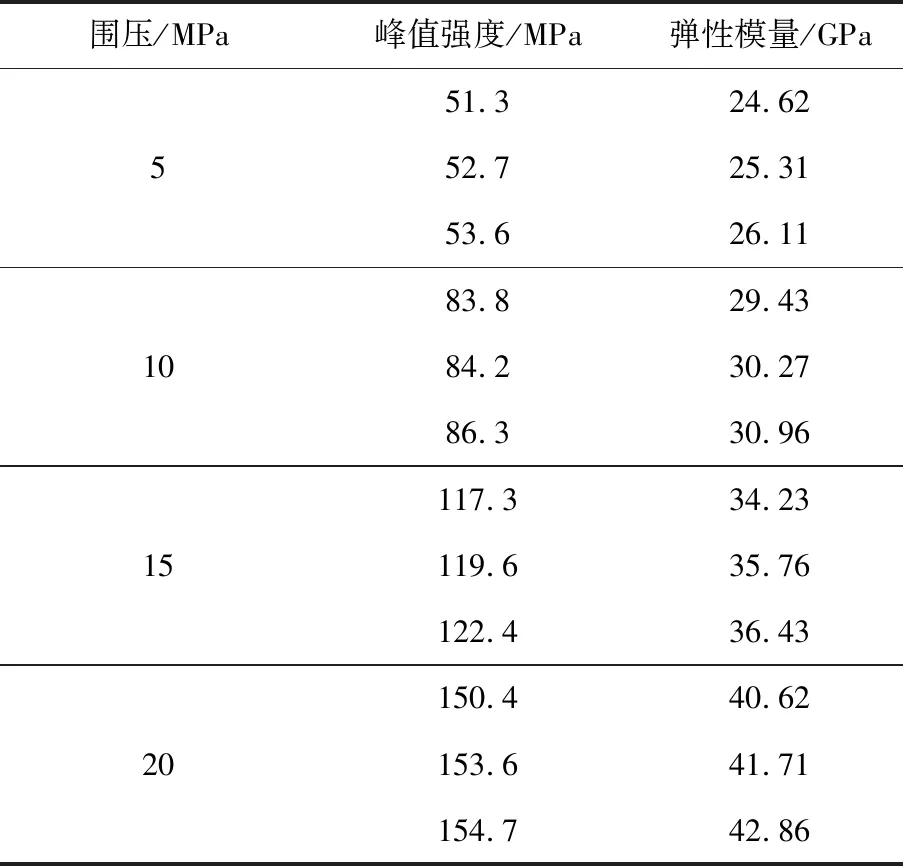
表1 不同围压下砂岩三轴强度参数Table 1 Triaxial strength parameters of sandstone under different confining pressures

图1 MTS812.02岩石三轴试验仪Fig.1 Rock triaxial tester of MTS812.02

三轴蠕变试验采用荷载控制的方式进行加载，首先以0.5 MPa/s的加载速率同步施加围压和轴压至预定的围压值后保持围压不变，继续以0.5 MPa/s的加载速率施加至预定轴向荷载值，并设定荷载持续时间为100 h。试验前准备工作有：① 事先在试样两端涂抹凡士林以降低试样两端与刚性垫片的摩擦损伤，避免端部效应；② 安装试样时尽可能保持横向位移传感器与试样底面水平，且轴向位移传感器的接触点要对称且水平。

根据表1中不同围压下的砂岩三轴强度参数确定三轴蠕变试验的各级应力水平：对于围压5 MPa的砂岩试样，峰值强度平均值为52.5 MPa，轴压初始荷载取其峰值强度的40%，取整为20 MPa；对于围压10 MPa的砂岩试样，峰值强度平均值为84.8 MPa，轴压初始荷载取其峰值强度的40%，取整为30 MPa；同理对于围压15 MPa的砂岩试样，轴压初始荷载取整为50 MPa；对于围压20 MPa的砂岩试样，取整为60 MPa，采用单体分级增量加载方式，其后分级增加10 MPa。若该时间段内试样发生破坏则停止该试验，选取新的试件进行蠕变试验。

其试验数据由试验机自动采集并换算成对应的应力-应变关系输出到数据采集系统，采样间隔为5 s，采用陈氏加载法将分级加载条件下的轴向蠕变-时间曲线转换成不同应力水平分别加载条件下的轴向蠕变-时间曲线如图2所示。

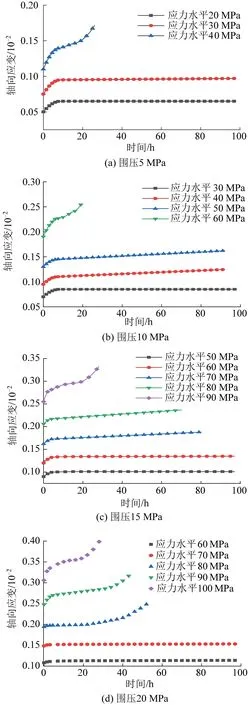
图2 不同应力水平下轴向应变-时间曲线Fig.2 Curves of axial strain - time under different stress levels

由图2可知，不同围压条件下轴向应变-时间曲线变化规律基本一致。在不同应力水平下均有瞬时应变产生，其瞬时应变值随应力水平的增加而增大，这是由于砂岩内部含有大量的原生微裂隙，加载初期使这些裂隙挤压闭合，使试件逐渐密实所致；但瞬时应变值占总应变值的比例先增加后减小，同时当蠕变变形进入衰减蠕变阶段后，衰减蠕变持续时间随应力水平的增加而减小；例如围压15 MPa情况下，轴压50 MPa时其瞬时应变0.091×10-2占总应变0.103×10-2的88%，轴压60 MPa时其比例增加至90%，而轴压70、80、90 MPa时其比例分别减小至86%、84%、77%，这是由于加载后期引起岩石内部不断损伤劣化和裂纹扩张贯通所致。而当应力水平较低时，砂岩进入稳定蠕变阶段，其蠕变速率接近于0，稳定蠕变持续时间较长至100 h时，砂岩未发生蠕变破坏；当应力水平中等时，砂岩进入亚稳定蠕变阶段，其蠕变速率不等于0，但仍未达到蠕变破坏的临界值；当应力水平较高时，砂岩进入加速蠕变阶段，这是由于高应力作用下岩石内部不断损伤劣化，累计至某一临界值时从亚稳定蠕变阶段末端进入加速蠕变阶段，未持续多长时间便发生蠕变破坏。

2 非定常西原模型的建立

2.1 一维非定常西原模型

传统西原模型由3部分构成：弹性元件、黏弹性部分和黏塑性，如图3所示。传统西原模型仅能很好地描述衰减蠕变和稳定蠕变的蠕变特性，对加速蠕变特性难以描述。图3中，E0为材料无损时的初始弹性模量；σs为屈服强度；E1为开尔文体弹性模量；η1和η2分别为开尔文体和牛顿体黏滞系数。

图3 传统西原模型Fig.3 Traditional Nishihara model

根据流变理论可知，传统西原模型的蠕变状态方程为:

(1)

式中，σ0为外荷载。

传统西原模型认为蠕变参数均为常数，不随时间和应力的变化发生劣化，但是实际深部围岩所处地质环境复杂，通常为高应力、强渗流和高温的环境，此时岩石在恒定荷载作用下产生蠕变变形时，岩石的力学参数和蠕变参数都会随着时间的增长而产生劣化，为了更好地描述深部围岩蠕变参数的劣化特性，引入损伤变量对其流变参数进行非定常变参，建立以屈服强度σs和长期强度σ∞为判别条件的非定常蠕变方程。

由文献[12-13]可知，岩石损伤应力阈值与岩石的长期强度一致，即当σ≥σ∞时，岩石才会发生损伤，损伤不断累积至进入加速蠕变阶段，在有限的时间内发生蠕变破坏。由文献[4]可知，岩石的屈服强度σs随着时间不断趋近长期强度σ∞，即σs≤σ∞。故当σ<σs且σs≤σ<σ∞时，应力水平未达到损伤应力阈值，即尚未进入加速蠕变阶段，其蠕变特性可用传统西原模型描述，蠕变方程满足式(1)。

当σ≥σs且σs<σ<σ∞时，岩石开始产生损伤，此时通过引入损伤变量D来描述岩石力学参数随着时间增长的劣化性质。一般情况下，可以通过应变等价性原理定义损伤变量，即

(2)

式中:D(t)为t时刻对应的损伤变量；Et为受损材料的弹性模量(有效弹性模量)。

而张强勇等[11]通过引入长期弹性模量E∞对式(2)进行改进，得到改进后的损伤演变方程为

(3)

式中：α为损伤程度相关系数。

根据文献[14]可知，岩石蠕变模型的弹性模量E(t)和黏滞系数η(t)与损伤变量D存在以下关系。

(4)

将式(3)代入式(4)中，得到弹性损伤元件和黏性损伤元件对应流变参数的非线性表达式为

(5)

(6)

根据式(6)结合西原体模型，得到弹簧元件和牛顿黏壶的损伤本构方程为

(7)

式中,εe(t)为弹性应变随时间变化关系式。

将式(5)和式(6)代入到式(7)中，结合一阶非齐次线性微分方程的求解方法得到弹性损伤元件和黏性损伤元件的蠕变模型为

(8)

(9)

将改进后西原模型中的弹簧元件和牛顿黏壶替换成式(5)、式(6)得到的元件，并串联一个加速蠕变触发的元件，可得非定常蠕变模型如图4所示。

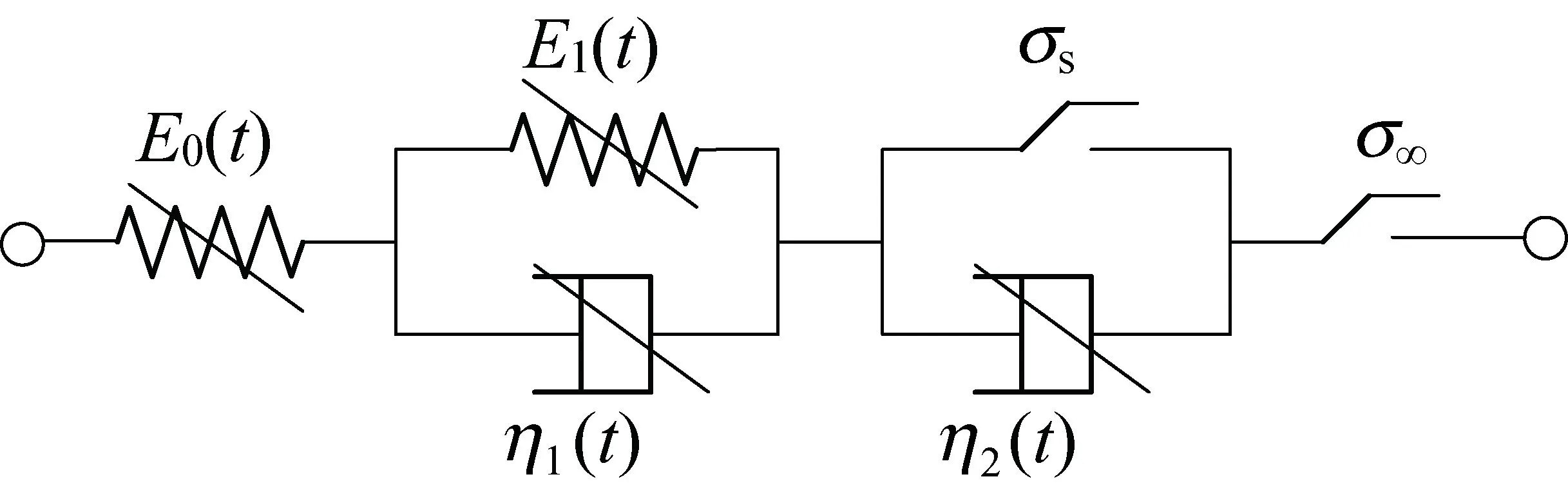
图4 非定常蠕变模型Fig.4 Unsteay creep model

当发生损伤即σ≥σ∞时，根据串联法则，一维状态下蠕变模型总应变ε满足如下条件：

ε=εe+εve+εvp

(10)

式中，εe为弹性应变；εve为黏弹性应变；εvp为黏塑性应变。

将弹簧元件的初始弹性模量E0代入式(8)中，可得弹性部分的变参数蠕变状态方程：

(11)

黏弹性部分由弹簧元件和牛顿黏壶并联而成，其本构方程为：

(12)

令σ=σ0，将σ=σ0和式(5)、式(6)代入式(12)中，两边进行LaPlace变换，可得：

(13)

式中：P为引入的一个复数参量；ε(p)为P满足的拉式函数。将式(13)中的P提取出来，可得：

(14)

对式(14)进行LaPlace逆变换，可得黏弹性部分的变参数蠕变状态方程[14]：

(15)

黏塑性部分由圣维南体和牛顿黏壶并联而成，当引入损伤变量时，其黏性元件进化为损伤体。根据并联法则可得黏塑性部分的本构模型为

(16)

当Maxwell模型中引入损伤变量时，黏滞系数η(t)的表达式可通过引入损伤因子D(t)进行表述，由此假设西原模型黏塑性部分的黏滞系数η2(t)表达式仍以损伤因子D(t)为参数，故结合式(6)，对式(16)进行Laplace变换和逆变换，得到黏塑性部分的变参数蠕变模型为

(17)

将式(11)—式(17)代入式(10)中，可得一维状态下非定常蠕变模型为

(18)

结合式(1)和式(18)可得一维状态下非定常西原模型蠕变方程表达式为

(19)

2.2 三维非定常西原模型的建立

实际工程应用中，围岩多处于三向受力状态，一维本构模型并不能较好地反映岩石的实际受力状态，故需要将一维本构模型推广至三维应力状态下。由文献[15]可知，岩石的三维蠕变本构方程与一维应力状态下具有一致性，可采用类比法[16]将一维物理模型的结果推广至三维流变分析中。

三向受力状态下，蠕变模型总应变εij满足如下条件

(20)

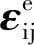
由于本文试验为假三轴试验，存在σ1>σ2=σ3；当岩石处于三向受力状态下，岩石内部的应力张量σij引起体积应变，可分解为球应力张量σm和应力偏张量Sij，应变张量εij引起形状畸变，可分解为球应变张量εm和应变偏张量eij，满足以下表达式[17]

(21)

式中，δij为Kronecker函数；σ1、σ2、σ3分别为3个应力方向的主应力；σm为球应力张量，εm为球应变张量。

由广义胡克定律知，球应力张量σm与球应变张量εm，应力偏张量Sij与应变偏张量eij的关系如下。

(22)

式中：K为体积模量；G为剪切模量；E为弹性模量；μ为泊松比。

由文献[18]可知，一维本构方程中的弹性模量E0推广至三维本构模型时由弹性剪切模量G0和体积模量K代替，一维中黏弹性模量E1推广至三维时由黏弹性剪切模量G1代替。结合式(5)、式(6)可得弹性剪切模量G(t)和黏滞系数η′(t)的表达式为：

(23)

三维蠕变模型中，弹性体的应变为

(24)

将式(21)和式(23)代入式(24)中，得到三维下弹性部分的应变为

(25)

假设体积变化属于弹性范围内，流变特性表现为剪切变形，则黏弹性部分的三维蠕变模型为

(26)

将式(21)和式(23)代入式(26)中，可得三维下黏弹部分的应变为

(27)

上述对于西原模型的弹性部分和黏弹性部分在三维状态下的蠕变方程，采用类比法进行推导是合适可行的，但是黏塑性部分由于涉及到屈服函数F和塑性势函数Q，并不能简单地采用应力张量Sij去替代一维模型中的应力σ，而应该通过屈服函数来确定[19-20]，一般情况下，F取德鲁克普拉格屈服函数为

(28)

黏塑性部分的三维蠕变方程为

(29)

其中，

(30)

式中:F0为岩石屈服函数的初始参考值，一般取F0=1；Q为塑性势函数，一般取F=Q；φ()取幂函数形式，一般取幂指数n=1[21]。

将式(23)、(28)和(30)代入式(29)中，得到三维下黏塑性部分的应变为

(31)

结合式(24)、(26)和(29)，得到当σ<σs和σs≤σ<σ∞时，三维状态下传统西原模型的蠕变方程为

(32)

将式(25)、式(27)和式(31)代入式(20)中，得到当σ≥σ∞时，三维状态下非定常蠕变模型方程为

(33)

结合式(32)和(33)可得，三维状态下三段式非定常蠕变模型方程为

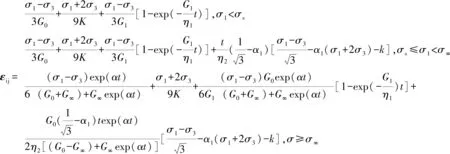
(34)

3 模型参数辨识

3.1 岩石强度的确定

由文献[22]可知，岩石屈服强度可通过三轴压缩试验确定。使用MTS812.02岩石试验系统对砂岩试样进行三轴压缩试验，设置围压为15 MPa，试验数据由试验机自动采集并输入到数据采集系统，整理可得围压15 MPa下砂岩的应力应变曲线如图5所示。由文献[22]可知，A点为屈服强度点，则砂岩的屈服强度σs=σA=60 MPa。

图5 围压15 MPa下应力应变曲线Fig.5 Stress-strain curve under confining pressure of 15 MPa

由文献[23-24]可知，在围压15 MPa情况下，等时应力应变曲线在应力水平80 MPa时呈现明显的发散现象，得到砂岩的长期强度为σ∞=80 MPa(图6)。

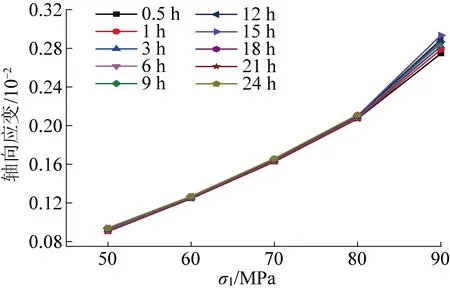
图6 围压15 MPa下等时应力应变曲线Fig.6 Isochronal stress-strain curve under confining pressure of 15 MPa

3.2 模型参数的确定

结合围压15 MPa下不同历时、不同应力水平的砂岩蠕变数据，通过Origin拟合软件对不同应力水平下砂岩蠕变试验数据与改进后蠕变模型进行拟合，得到不同应力水平下非定常蠕变模型参数值见表2，其中不存在数值的参数用“—”表示。由图7可知，不同应力水平下砂岩蠕变试验数据值与相对应非定常蠕变模型理论值具有较好的拟合度。图7中图7a验证了以屈服强度σs作为岩石蠕变曲线从稳定蠕变进入亚稳定蠕变阶段的判别条件的合理性；图7b验证了本模型中屈服函数F取德鲁克普拉格函数的可行性；图7c验证了引入长期强度σ∞作为损伤应力阈值以及进入加速蠕变阶段的判别条件的合理性；图7d验证了引入损伤变量D(t)对弹性剪切模量G(t)和黏滞系数η′(t)进行非定常变参的可行性。

表2 模型参数Table 2 Model parameters

图7 围压15 MPa下不同应力水平拟合曲线Fig.7 Fitting curves of different stress levels under confining pressure of 15 MPa

综上，不同应力水平下砂岩蠕变试验数据与相对应非定常蠕变模型理论值吻合程度较为理想，曲线变化趋势基本一致，决定系数均达到了0.97以上，说明了该模型引入屈服强度σs和长期强度σ∞作为蠕变阶段判别条件的合理性。该模型不仅仅充分反映出砂岩加载后的瞬时弹性应变，还较好地反映出第一阶段的衰减蠕变和第二阶段的稳定蠕变(亚稳定蠕变阶段)，特别是该模型克服了传统西原模型难以描述的加速蠕变阶段，较好地呈现不同应力水平下砂岩的蠕变曲线类型，说明了建立考虑弹性模量退化的非定常蠕变模型的正确性与合理性。

3.3 损伤劣化规律

通过对表2数据的分析表明，在围压15 MPa条件下，应力水平为50、60、70 MPa时G∞数据不存在，进一步证明了“引入长期强度σ∞作为损伤应力阈值以及进入加速蠕变阶段的判别条件”观点的正确性。应力水平为80 MPa时，将G0=8.176 MPa、G∞=2.834 MPa及α=0.002 9代入式(3)中进行反演，得到方程D(t)=0.653 4[1-exp(-0.002 9t)]，同理将应力水平为90 MPa下的G0=6.939 MPa、G∞=2.405 MPa及α=0.002 9代入式(3)进行反演。

将损伤演化方程代入式(23)中，可得砂岩流变参数的损伤衰减方程为X(t)=X0[0.653 4exp(-0.002 9t)+0.346 6]，其中X可表示弹性剪切模量或黏滞系数，X0表示其初始值，如图8所示。

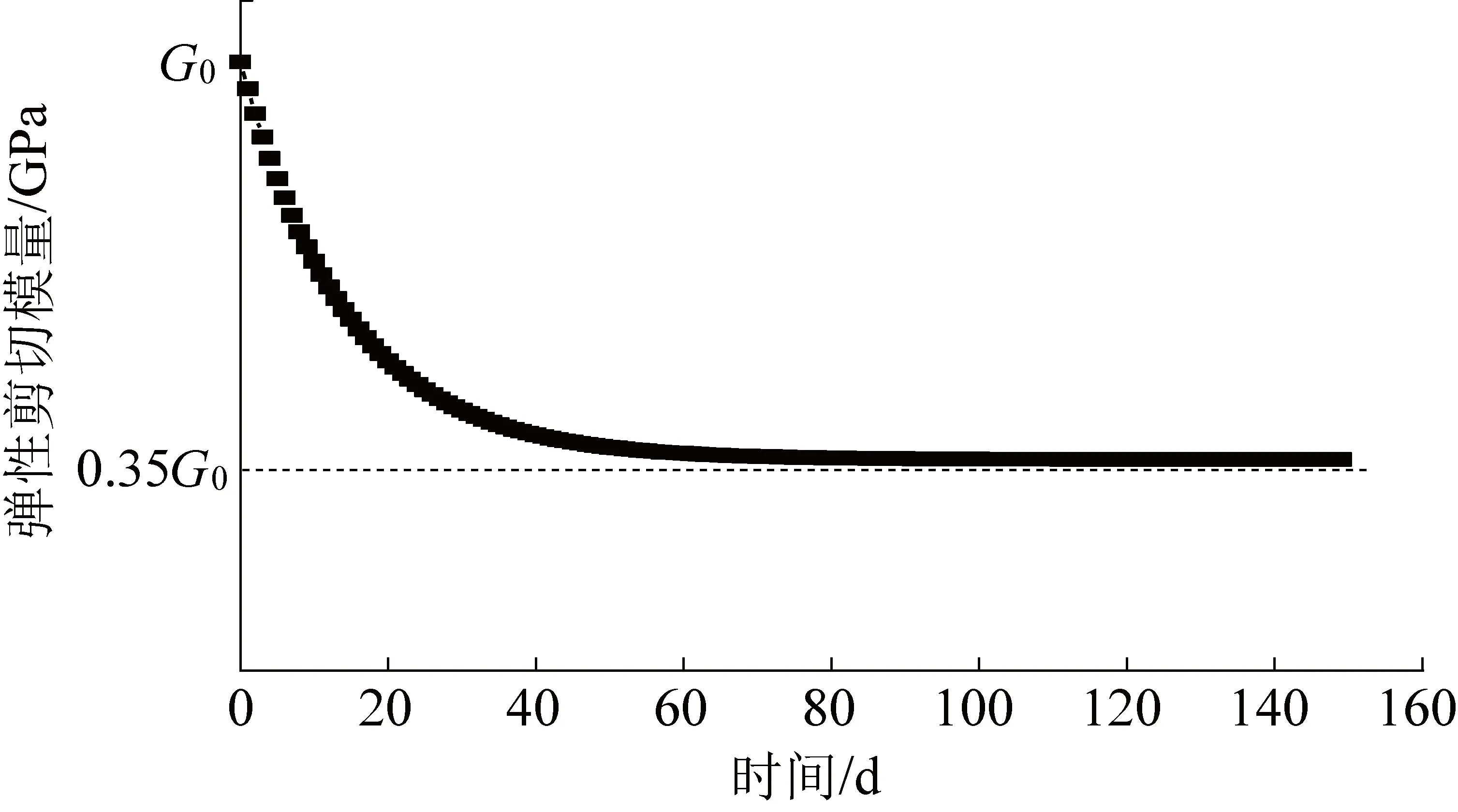
图8 损伤衰减曲线Fig.8 Damage attenuation curve

结合辽宁阜新海棠山隧道的现场围岩应变监测数据见表3，取流变参数初始值G0=6.939、G1=7.574、η1=0.158、η2=1.829，将表3中现场监测数据代入式(34)中，可得各流变参数变化如图9所示。

表3 遂道围岩应变变化现场监测数据Table 3 Strain change field monitoring data

图9中G0、G1、η1、η2的变化趋势与图8流变参数衰减趋势基本一致，反映了流变参数的损伤劣化规律：弹性剪切模量与黏滞系数的衰减规律基本一致，随时间的增长，流变参数呈负指数衰减，大约经历80 d的损伤劣化，流变参数趋于一个稳定值，其稳定值与初始值的比值为0.35。表明实际工程中由于高应力作用导致的岩石流变参数损伤现象十分严重，值得引起广大学者的关注。