基于DNN与IMPDE的武器系统效能优化

王国梁，赵 滟，杨卓鹏，杨 超

(中国航天系统科学与工程研究院，北京 100048)

1 引言

武器系统效能是指武器系统能够满足(或完成)一组特定任务要求的量度。如何在效能参数阈值内，寻找到最佳参数组合，达到效能最大化，是武器系统效能优化的实质。由于影响武器效能的因素众多，这些因素间的相互关系是不确定的，与系统效能的关系也是不确定的。如何确定这些指标参数，从而使武器系统的效能值最大，对于武器的论证、研制、改进具有重要的现实意义。

进化算法作为一种智能优化算法，由于不依赖于解析模型和梯度信息，不进行求导操作，不存在函数连续的约束，并具有很强的全局搜索能力，因此在武器系统效能优化问题上已经得到了应用。汪民乐等设计了新的编码方案和遗传算子，采用改进遗传算法对战术导弹靶场效能进行了优化研究；黄昆鸟等结合系统效能神经网络仿真模型构造的目标函数和混合遗传算法对末敏弹进行了系统效能参数优化设计；李志猛等采用经典的多种群遗传算法对常规导弹综合火力打击效能进行了优化研究；黄凤华等以灰色神经网络构造的仿真模型作为目标函数，采用遗传算法对末敏弹进行了系统效能参数优化设计；汪乐民等设计了一种采用实数编码的多目标遗传进化算法用于求解导弹对面积目标射击效能的优化模型；林涛等将组合差分进化算法引入作战仿真环节，解决了效能优化目标函数难以构建的问题，并为武器装备作战效能的优化提供了手段；张磊潇等通过效能分析建立了舰艇综合防御鱼雷作战决策优化模型，并采用遗传算法求解优化模型。

武器系统效能优化问题具有多变量多峰值的特点，而当前武器效能优化所采用的智能优化算法，在面对此种情况，显现出优化效率低，优化结果不稳定的问题。为此，本文结合深度神经网络建立的系统效能模型，提出一种改进多种群差分进化算法，并对其优化效果和性能进行了对比分析。

2 基于深度神经网络的武器系统效能模型

深度神经网络具有高度非线性映射能力，是一种有效的多层神经网络学习方法，其主要特点是信号前向传递，而误差后向传播，通过不断调节网络权重值，使得网络的最终输出与期望输出尽可能接近，以达到训练的目的。

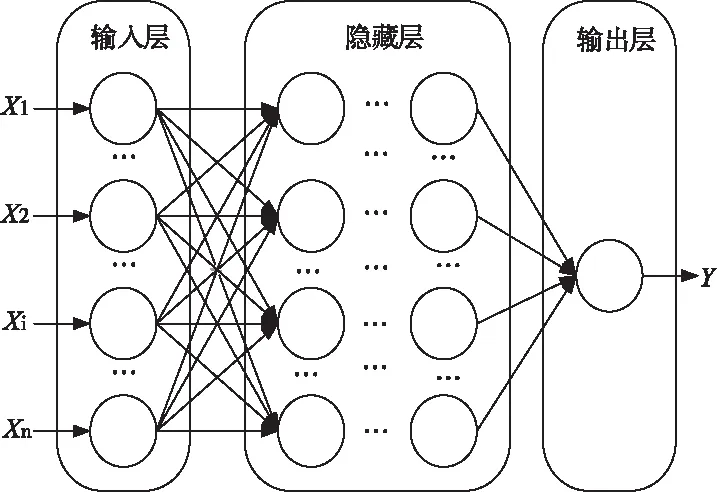
图1 深度神经网络结构图

Z

[]=

W

[]·

A

[-1]+

b

[]

(1)

激活函数

g

[]：

(2)

成本函数

J

(

w

，

b

)为：

(3)

利用得到的误差值进行逆向传播，并采用梯度下降法对神经元权值

W

[]和阈值

b

[]进行修正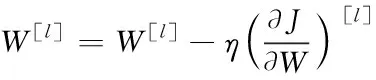

(4)

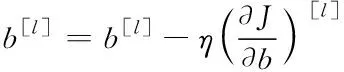
(5)

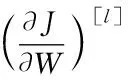
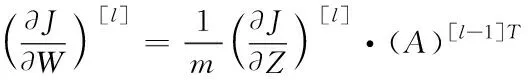
(6)

(7)

(8)

(9)

由于影响防空导弹武器系统效能的因素太多，这里选取发射车辆(

C

1)、平均故障间隔时间(

C

2)、平均修复时间(

C

3)、导弹飞行速度(

C

4)、最大射程(

C

5)、发射质量(

C

6)、导弹数量(

C

7)、目标通道数(

C

8)、系统反应时间(

C

9)、最大探测距离(

C

10)、制导精度(

C

11)、单发杀伤概率(

C

12)、指挥控制能力(

C

13)、机动力(

C

14)等作为影响因素。

由于训练样本的数量与质量关系到深度神经网络模型的仿真可信度，而实际中防空导弹武器系统效能数据样本较少。故通过文献[11]所提方法对已有样本进行了扩增。由此获得800组数据，并采用离差标准化法对数据中量纲类性能指标进行归一化处理，归一化后的数据样本见表1。

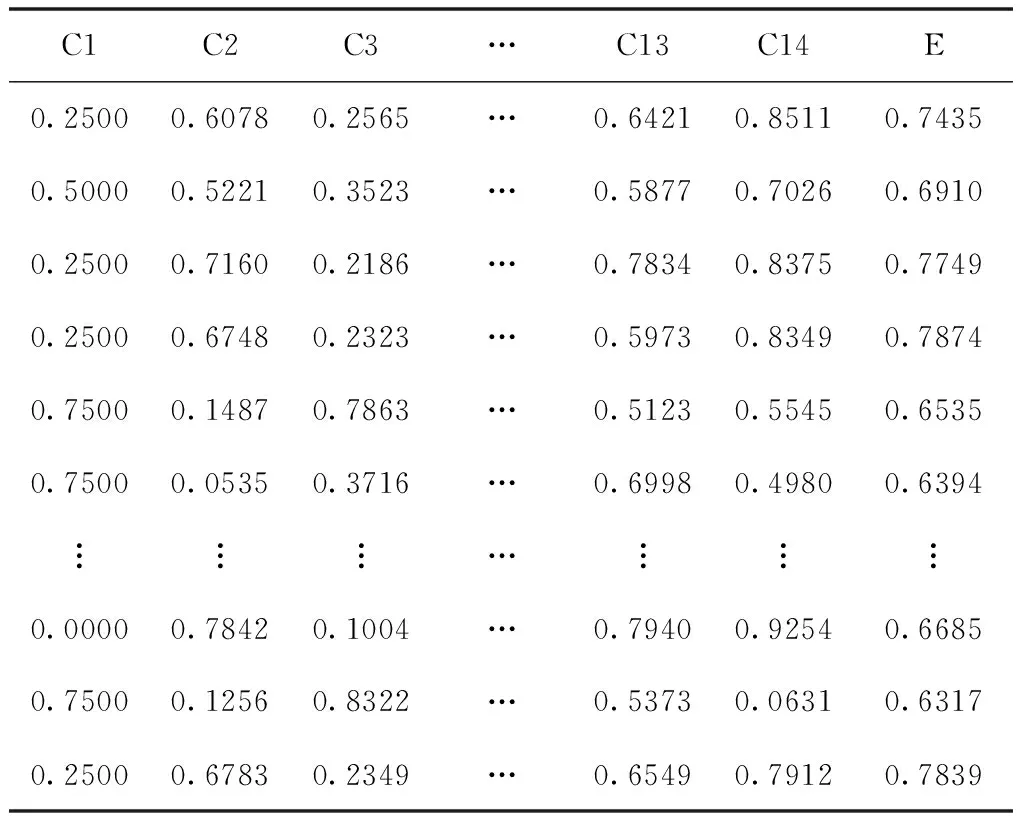
表1 归一化后的数据样本

使用上述训练样本训练深度神网络。通过信号的前向传播与误差值的反向传播理论，利用式(1)-式(9)，最终得到一个基于深度神经网络的系统效能模型，即系统效能优化函数：

(10)

3 改进多种群差分进化算法

3.1 差分进化算法

差分进化算法(Differential Evolution Algorithm，DE)是一种高效的全局优化算法，是将种群中的向量作为寻优个体，利用向量之间的加减、缩放以及互换信息来进行种群的更新，不断生成新的子代，通过适应度选择最后向最优值收敛。该算法的基本思想是：从随机生成的初始种群开始，通过差分变异和交叉不同个体所携带的信息以产生新的种群，比较产生的新种群与原始种群中相应个体的适应度，将优势向量保存到种群中，将劣势向量淘汰，引导搜索向最优解逼近。差分进化算法的流程图如图2。

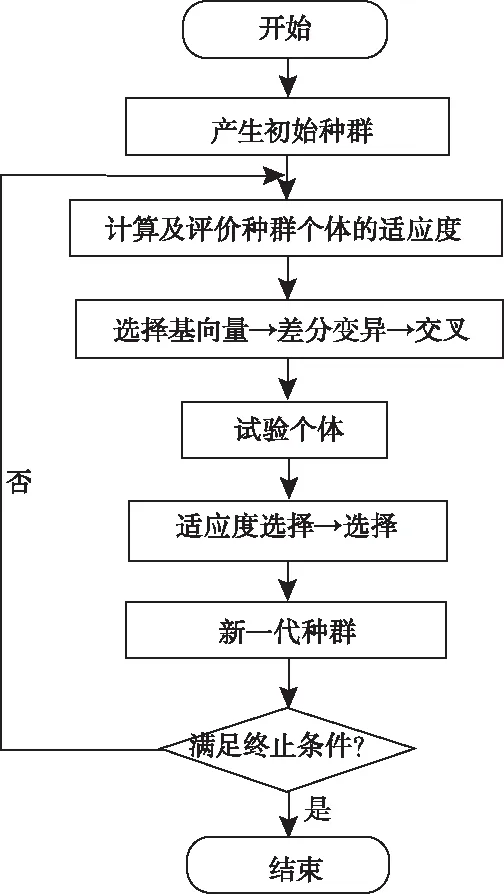
图2 差分进化算法流程图

其主要步骤可总结如下：

1)种群的初始化。DE算法可在解空间中随机产生

M

个个体，每个个体由

D

维向量组成：

X

=(

x

，1，

x

，2，

x

，3，…，

x

，，)。第

i

个个体的第

j

维值取值方式如下：

x

，=

x

min，+

rand

(0，1)(

x

max，-

x

min，)

(11)

式中：

i

∈(1，2，…

M

)，

j

∈(1，2，…

D

)，

x

max，、

x

min，分别为

x

，取值的上下界；

2)计算种群个体适应度。适应度是用于度量群体中各个个体在优化计算中有可能达到或接近于最优解的优良程度。通常可直接选择目标函数或依据变换规则对目标函数进行变换得到适应度函数。其中，线性变换可表示为

F

′=

α

*

F

(

X

)+

β

(12)

式中：

F

(

X

)为目标函数，

F

′ 为变换后的适应度函数，

α

、

β

由目标函数的平均值和变换后的适应度函数最大计确定；3)差分变异操作。基本的差分变异为

DE/rand/

1变异，指随机选取多个父代种群中代表不同个体的向量，通过向量之间的加减缩放运算，得到区别于父代种群的变异个体，实现可行解空间中不同区域的优化，其表示为

H

(

n

)=

X

(

n

)+

F

·(

X

(

n

)-

X

(

n

))

(13)

其变异方式还有很多种，在这里只列出DE/target-to-best/1变异方式，可表示为

H

(

n

)=

X

(

n

)+

F

(

X

(

n

)-

X

(

n

))+

F

(

X

(

n

)-

X

(

n

))

(14)

式中，

n

为第

n

代，

X

(

n

)为当前个体，

p

，

p

，

p

∈[1，

M

]，且

X

(

n

)≠

X

(

n

)≠

X

(

n

)，

X

(

n

)为当前最优个体，

F

为变异因子；4)交叉。

DE

算法通过变换目标向量

X

和变异向量

H

间的部分信息生成新的个体，进而提高种群的多样性，并将变异个体与原个体统称为试验个体存放在试验种群中，二项交叉操作可表示为：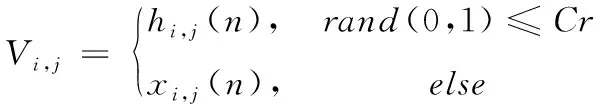

(15)

式中，

Cr

为交叉概率；

V

，为试验个体；

5)选择操作。通过一对一生存竞争，比较原向量与目标向量间的适应值，选择保留更高适应值的个体，进而生成新一代种群，完成种群的更新迭代。选择操作可表示为：

(16)

3.2 改进多种群差分进化算法(IMPDE)

基本差分进化算法及其变种算法在单独用于处理复杂的多维变量、多峰值、非线性程度高的问题时，容易出现停滞现象，收敛到局部最优。为了更稳定、准确地获得导弹武器系统效能的最大化，引入多种群协同进化策略和参数自适应调整策略，结合DE/rand/1/bin与DE/target-to-best/1/bin算法，提出了改进多种群差分进化算法(IMPDE)。其核心思想是将种群分为多个子种群，并利用DE/rand/1/bin算法在优化过程中可维持种群多样性以及DE/target-to-best/1/bin算法快速寻优的特点，对种群进行进化操作。其中，奇数种群采用DE/rand/1/bin算法，且迭代次数与外部循环保持一致，偶数种群采用自适应DE/target-to-best/1/bin算法，且内部设置单独循环，经过一定代数后，种群间进行个体迁移。这种混合模式不仅保证了种群的多样性，防止出现“进化停滞”，陷入局部最优，而且可以快速收敛到最优值，提高了算法的稳定性与准确性。

其实现过程如下：

1)生成和分配多种群。采用实整数编码规则进行编码，在可行解空间内，由式(11)随机初始化生成K个染色体，并将其按一定规模分配给NP个种群；

2)计算及评价种群个体适应度。由式(12)对目标函数式(10)进行线性变换得到适应度函数，评价并记录种群个体的适应度；

3)多种群协同进化。

对奇数种群采用DE/rand/1/bin算法进行进化操作。遍历种群列表，为不同的奇数种群设置不同的变异因子和交叉概率，以等差数列的方式在F(0.4～1)和Cr(0.5～1)内取值；然后由式(13)、式(15)和式(16)，计算得到新一代种群；

对偶数种群采用DE/target-to-best/1/bin算法进行进化操作。首先依据文献[14][15]设置自适应的变异因子与交叉概率，公式分别如下：

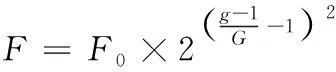
(17)

(18)

其中，

F

=0

.

2为初始变异因子的值，

g

为当前迭代次数，

G

=10为独立循环的最大迭代次数，[

Cr

，

Cr

]=[0

.

3，0

.

9]为交叉概率的变化范围，

c

为初始种群平均适应度方差，

c

为第

g

代种群平均适应度方差的允许值，

c

(

g

)为第

g

代种群平均适应度方差；然后，由式(14)～式(16)，计算得到新一代种群；最后以最大进化代数作为循环的终止依据；

4)循环操作。采用最大进化代数作为终止判据，若达到最大进化代数；则终止进化，否则进入下一步；

5)群间个体迁移。迁移条件设置为每进行2代，开展1次迁移。以环状结构为迁移结构，根据迁出概率，从迁出种群中择优选择迁出个体，择劣替换待迁入种群中的个体，流程图如图3。

图3 改进多种群差分进化算法流程图

4 实验设计及结果分析

本文以防空导弹武器系统效能最大化作为优化目标，其效能优化函数即式(10)，并以表2所列的因素作为优化参数，经归一化处理后，转为输入变量。

表2 效能优化参数

按照上述基于IMPDE算法的导弹武器系统效能优化方法，解的系统参数的最佳组合为：发射车辆C=3，平均故障时间C=220.5h，平均修复时间C=1.42h，导弹飞行速度C=2.250马赫，最大射程C=4.212km，发射质量C=14.67kg，导弹数量C=4，目标通道数C=3，系统反应时间C=3s，最大探测距离C=18.75km，制导精度C=0.65m，单发杀伤概率C=0.74，指挥控制能力C=0.80，机动力C=98.5km/h。此时防空导弹武器系统效能最大为0.7874。

为进一步分析改进算法在防空导弹武器系统效能优化过程中的效果及性能，采用结果对比来验证，对比的算法为：

● DE/rand/1/bin(算法1)

● DE/target-to-best/1/bin(算法2)

● 基于算法1的多种群差分进化算法(算法3)

分别采用算法1、算法2、算法3、改进多种群差分进化算法(IMPDE)对基于深度神经网络的系统效能模型进行寻优。其中进化代数设置为1000代，IMPDE算法种群规模为(60，60，60)；算法1和算法2的种群规模为60，变异因子F和交叉概率Cr采用固定参数(0.5，0.5)；算法3的种群规模为(60，60，60)，不同的种群以等差数列的方式在F(0.4～1)和Cr(0.5～1)内取值。每个算法依次进行100次实验，预设精度为0.00001，分别统计最优值、最差值、均值与标准差，以及100次实验中各个算法进化结果进入预设精度的成功率，并将其作为各算法稳定性的评价指标。各算法进行100次实验的进化结果如表3所示。

表3 各算法进行100次实验的进化结果

由表3数值进行分析。通过100次实验，在规定精度内，改进算法与三种对比算法都有机会寻找到最优值，即效能最大值；但四种算法在收敛稳定性上差异较大，由最优值与最差值的范围可获知，IMPDE算法的收敛结果在极小的范围内波动，算法1和算法3的波动较小，算法2的波动范围则较大；由均值和标准差可知IMPDE算法每次运行的结果基本分布在最优值附近，成功率达到100%，算法1和3大多分布于最优值处，部分处于0.780附近，推测原因为陷入局部极值，算法2的分布最为离散，且其成功率仅为43%。这种差异在图4中表现的更为直观，各算法进行100次实验的进化结果分布如图4所示。由此可得，从算法收敛精度和稳定性角度结合来看，改进多种群差分进化算法(IMPDE)表现的要优于三种对比算法。

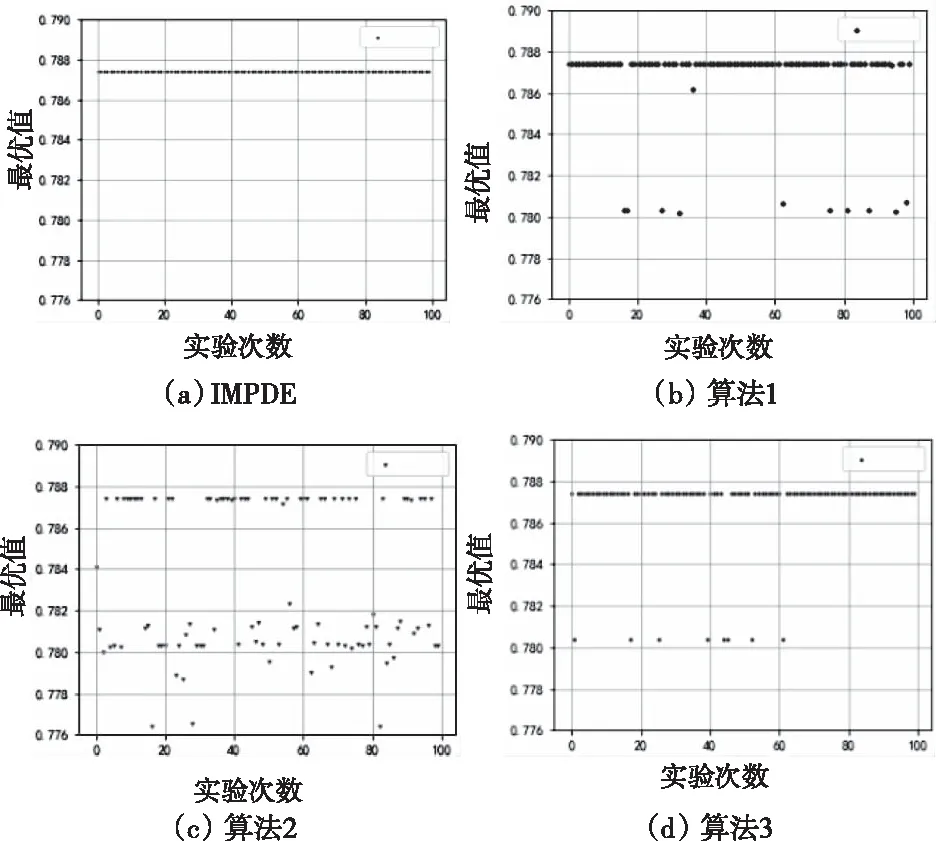
图4 各算法进行100次实验的进化结果分布

由于对比算法的优化结果存在不确定性，导致优化过程不尽相同，故此处只选取IMPDE算法其中一次实验的优化过程进行展示，IMPDE算法在优化过程中种群个体最优目标函数值与种群个体平均目标函数值变化曲线如图5所示。

图5 IMPDE算法在优化过程中目标函数值变化曲线

由图5中两条变化曲线可知，IMPDE算法在整个优化过程中，种群中个体的目标函数值分布较广，维持了种群个体的多样性，有力地避免了在进化后期陷入局部极值的现象，且种群在180代左右时已接近目标函数的最优值，从收敛速度的效果来看，本文所提算法可以较为快速的达到收敛。

从上述所有结果可以看出，当面对多变量多峰值函数时，在同样维度的条件下，改进多种群差分进化算法相较于对比算法在收敛精度、收敛速度和稳定性以及维持种群个体多样性方面皆具有较大的优势，并且这种效果随着变量个数增多或峰值范围变大而更加显著。

5 结语

本文以防空导弹武器系统效能优化为研究对象，根据系统效能优化问题涉及因素复杂，难以稳定、准确地获得最佳参数组合，达到系统效能最大化的难题，提出了改进多种群差分进化算法(IMPDE)，并将该算法与基于深度神经网络的系统效能模型相结合。通过对比实验，表明了本文所提算法在系统效能优化问题中具有较好的寻优效果，为实现导弹武器系统效能研究提供了新的方法和手段。