螺旋桨滑流对环形进气道性能影响的数值仿真
2022-07-20杨成凤段卓毅丁兴志
杨成凤,段卓毅,张 宏,丁兴志
(航空工业第一飞机设计研究院,陕西 西安710089)
1 引言
涡轮螺旋桨发动机在低亚音速飞行时具有拉力大、耗油率低、推进效率高等优点,广泛应用于军民用飞机运输机领域。同时螺旋桨飞机还具有低速飞行时升力大,起飞、着陆时的飞行速度低等特点,对跑道的依赖程度低,在舰载机领域也有广泛应用。独特的动力形式赋予了涡桨飞机一系列优势的同时,也带来设计中不可避免的螺旋桨滑流效应、气动干扰等问题。涡轮螺旋桨发动机进气道位于螺旋桨后,其性能直接受螺旋桨滑流的影响,过大的进气道出口总压畸变会引起发动机不稳定工作甚至失速喘振。因此,开展螺旋桨滑流与进气道气动性能影响的研究具有重要意义。
针对螺旋桨滑流的研究多集中于滑流对全机气动力影响方面的数值仿真及试验研究,其中包括螺旋桨滑流等效盘模型的应用、滑流对机翼绕流流场的影响分析、螺旋桨滑流与飞机主要部件的气动干扰研究等。螺旋桨数值仿真的方法主要有多重参考系(MRF)法、滑移网格非定常法和动量源法。这些技术同样可用于模拟螺旋桨滑流与进气道相互干扰的数值仿真中。文献[16]对军用运输机A400M的螺旋桨短舱进气道模型的气动性能进行了研究,将动量源法和滑移网格非定常法得到的仿真结果与试验结果进行对比,结果表明滑移网格非定常法比动量源法得到的仿真结果与试验结果更相近。文献[17]对高负荷涡轮螺旋桨飞机进气道的性能稳定性进行了数值分析,用数值方法分析进气道几何参数对进气道气动性能的影响规律,结果表明大曲率半径的S弯进气道能够有效抵消由螺旋桨滑流引起的进气道总压畸变指数的增加。
动态重叠网格方法的实质是采用覆盖整个计算域的母网格和运动物体的子网格叠加来描述物体间的相对运动, 其关键是要实现各重叠网格间数据准确、快速地交换。该项技术是模拟多体运动干扰问题的关键技术,国内外开展了大量的算法研究及应用分析工作。在国外,Meakin 等采用了结合贴体网格和笛卡儿网格的动态重叠网格, 求解黏性N-S方程,Kazuhiro在1999年提出了基于非结构网格的重叠网格方法,Rober对非结构重叠网格间信息交换插值方法进行了详细研究;在国内, 李孝伟等采用了结构网格动态重叠方法模拟外挂物投放, 缪涛等采用结构网格动态重叠方法模拟了尾翼对螺旋桨滑流的影响,夏健等采用了非结构重叠网格和并行算法模拟了三维多体相对运动绕流流场,周铸等研究了一种适用于三维复杂外形各种网格拓扑结构的多块重叠网格技术。
本文研究了一种位于螺旋桨根部的环形进气道,受旋转螺旋桨叶片根部复杂流场的影响,进气道的总压恢复系数和畸变指数都发生了很大变化,这与其它机型的螺旋桨滑流的影响机理是不同的,国内外对此方面的研究鲜见相关资料报道。采用动态重叠网格计算了非稳态滑流流场。首先,针对典型构型进行了不同湍流模型下的算例验证,验证模拟方法的准确性;其次,对比分析了地面无风状态、带风速状态、侧滑状态等三个典型状态下有/无螺旋桨滑流对进气道气动性能的影响,归纳总结了各个状态下的滑流影响机理及定量影响结果。
2 数值模拟方法及算法验证
2.1 数值模拟方法
计算采用动态重叠网格方法多节点并行求解非定常雷诺平均N-S方程,湍流模型采用k-ω SST两方程模型。在时间上计算采用双时间步方法,每个真实时间步桨叶在周向运动3°,即每个旋转周期包含真实时间步数为120步,每个真实时间步内的子迭代步数为50步,采用隐式LU-SGS方法进行迭代,空间格式采用Roe通量差分分裂方法。
在采用时间精确的数值方法求解中,网格运动是一个比较棘手的问题,本文采用的方法是结构网格框架下的动态重叠(Chimera)网格方法。重叠网格对相对运动的部件生成不同的网格,分别随各自部件运动,相互之间构成动态的重叠关系。由于部件运动的关系,有必要在网格生成上对运动路径上的网格进行互相适应,照顾好这个区域的网格密度以及均匀程度,以满足重叠插值的要求;同时要求不同部件的网格在接合区域相互匹配,以适应于流场的光滑过渡。
2.2 算法验证
为了验证计算方法,对单独涡桨发动机吊舱带六片桨叶模型(见图1)进行了计算,将计算结果与试验结果进行对比。螺旋桨直径4m,桨叶角为36°,转速为7550转/分,来流风速25m/s,攻角为0°,模型缩比为1:12。
计算网格采用重叠网格方法。分别对运动部件(桨叶及轮毂)和静止部件(发动机吊舱)生成各自的网格,图2中给出了桨叶网格和发动机吊舱背景网格的重叠关系,桨叶网格随桨叶一起作刚体运动,动态地与发动机吊舱背景网格构成重叠关系。桨叶网格的拓扑结构为O型,为了模拟粘性附面层的需要,第一层网格距离物面的距离约为0.01 mm。网格单元总数约330万。

图1 带六片桨叶的涡桨发动机外形

图2 桨叶网格和短舱背景网格的重叠关系
图3给出的是螺旋桨效率计算结果与试验结果的比较,相比SA湍流模型而言,SST湍流模型的计算结果与试验值吻合更好,误差最大不超过3%,因此在以后的计算中均采用SST湍流模型。涡桨发动机吊舱带六片桨叶模型的计算结果证实了动态重叠网格及非定常方法解算器的可靠性,可用于飞机带螺旋桨滑流的气动特性计算分析。
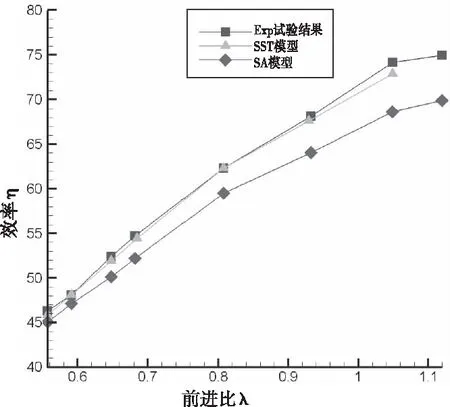
图3 螺旋桨效率计算结果与试验结果的比较
3 简化模型和网格划分
图4给出了本文计算简化构型,包括简化机身、机翼、螺旋桨及发动机短舱。进气道是位于短舱前部、由螺旋桨整流锥和短舱内整流罩构成的环形进气道,后部安装有6个整流支板,整流支板的位置如图6(c)所示。进气道出口面位于整流支板后部,出口边界条件设置在一段等值段的后部,为压力出口边界。由于双发螺旋桨是同向旋转,为了对比研究侧滑状态下的双侧进气道性能,机身对称面设置为对称面边界条件,即计算域实际为一个完整的机身+双侧螺旋桨进气道短舱构型。
计算构型分为无动力构型和带动力构型,无动力构型仍然包括螺旋桨,只是螺旋桨不旋转,为定常计算,带动力构型螺旋桨旋转,为非定常计算。

图4 计算构型各部分示意图
计算中采用多块结构网格,对于定轴旋转的螺旋桨,采用重叠网格方法。对螺旋桨与背景网格交接处、主发进气道内流区域进行适当加密,其余区域网格光滑保持过渡,全机网格量约7600万。全机外流网格与进气道内流网格如5所示。

图5 计算域网格
涡桨发动机进气道性能指标主要包括:进气道出口面上的总压恢复系数及总压畸变指数,定义如下
1)总压恢复系数
σ
=P
/P
∞(1)
式中,P
为进气道出口截面上的流量加权平均总压,P
∞为前方来流的总压。2)总压畸变指数
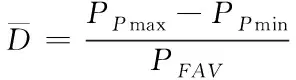
(2)
式中,P
max为进气道出口截面最大总压,P
min为进气道出口截面最小总压,P
为进气道出口面上的平均总压。计算状态见表1。

表1 进气道性能计算状态表
4 计算结果分析
4.1 地面无风速状态滑流对进气道性能的影响
地面无风状态下(计算状态1)的流场如图6所示,唇口绕流是其主要特征,由于环形进气道唇口相对较钝,绕流不易产生流动分离,主要的总压损失来源于气流与整流锥及短舱内整流罩壁面之间的摩擦损失,因此该状态下,进气道畸变指数相对较低,不考虑螺旋桨滑流影响时,约为8.88%,另一方面,由于双侧壁面都有附面层,因此与短舱进气道相比,其总压恢复系数相对降低,约为0.98左右,而短舱进气道总压恢复系数约为0.99左右。环形进气道位于螺旋桨的后方,螺旋桨根部的绕流将对进气道气流的流场品质产生影响,由于地面状态下的流场特征为唇口绕流,因此与带风速等其它状态相比,该状态下的螺旋桨绕流影响相对是较小的,图7和图8给出了带桨状态下的有/无动力计算结果对比,带动力构型为非定常计算结果,由于是6叶桨,每个桨叶旋转60°之后与另一片桨叶位置重合,因此本文给出了单片桨旋转至20°、40°、60°等三个角度时的进气道出口面上的流场信息,即对应60°周期的T/3、2T/3及T。对比有/无动力下进气道出口面上的总压恢复系数图谱和马赫数图谱及有/无动力下的总压恢复系数和畸变指数,可见:在螺旋桨增压作用下,环形进气道的总压恢复系数增大了1.4%,畸变指数增大了约2%,受导流支板的影响,总压恢复系数图谱和马赫数图谱都被分割成了6个区域,6个区域的图谱分布相差不多,支板后部的尾流区为低能区,带动力后,低能分割区变成6个旋转蜗壳状,靠近外壁面出现了6个低能区,主要是叶片根部拉起来的分离区造成的。

图6 地面无风速状态下流场

表2 进气道的总压恢复系数和畸变指数对比结果(地面无风速状态)
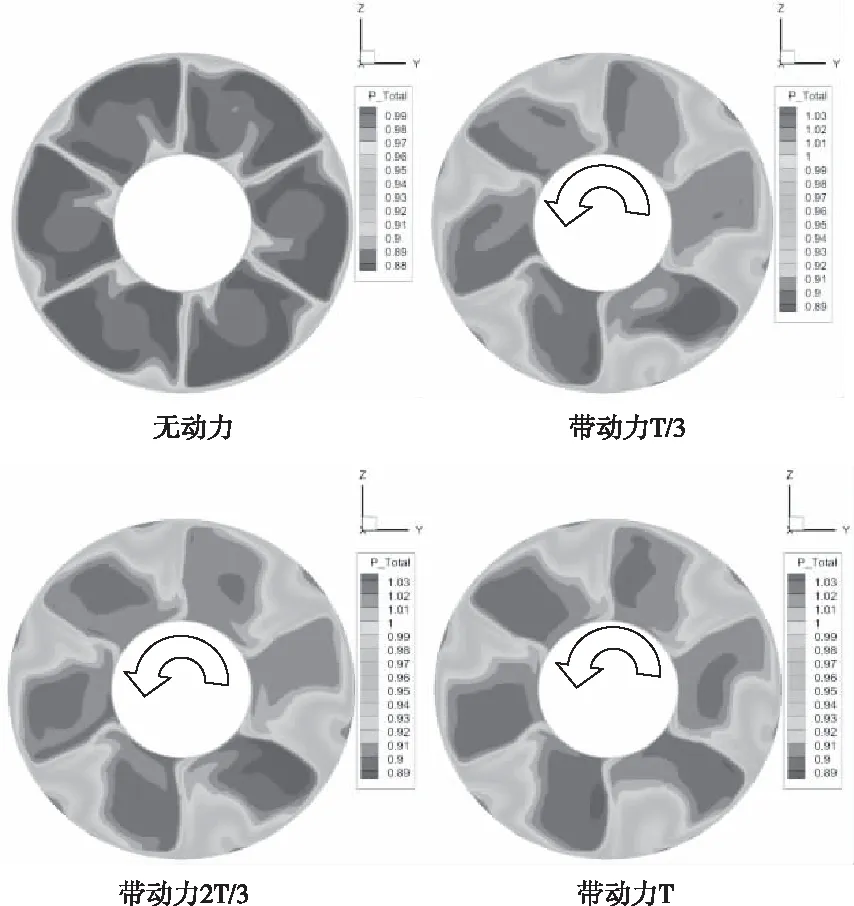
图7 地面无风速状态下进气道出口截面上的总压恢复系数图谱

图8 地面无风速状态下进气道出口截面上的马赫数图谱
4.2 带风速状态下滑流对进气道性能的影响
带风速状态下(计算状态2和3)的流场如图9所示,从图中可以明显看出螺旋桨后滑流的偏转方向,从前往后看,螺旋桨为右旋(从后往前看是左旋),这也造成了进气道出口面上总压图谱形成了左下区域高、右上区域低的非均匀分布形式。带动力后,滑流增压作用使进气道总压恢复系数提高约3%,畸变指数增大4%-5%。低马赫数状态下的进气道性能优于高马赫数状态下的进气道性能。文中所有图谱均为从后往前看的视角(顺航向)。
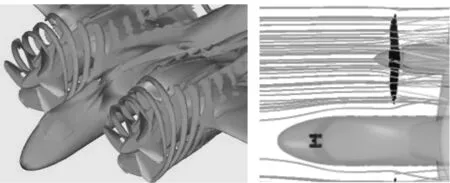
图9 M=0.18,a=15°状态下的流场
图10给出了带迎角状态下进气道出口面上的总压恢复系数图谱,从无动力图谱上可见,外环壁面附近出现了6个低能区,这主要是因为无动力构型也带着静止不动的螺旋桨进行的计算,该低能区是由叶片根部拉起的分离涡形成的。带动力后,环形进气道上部偏右出现低能区,畸变增大。

表3 进气道的总压恢复系数和畸变指数对比结果(带风速)
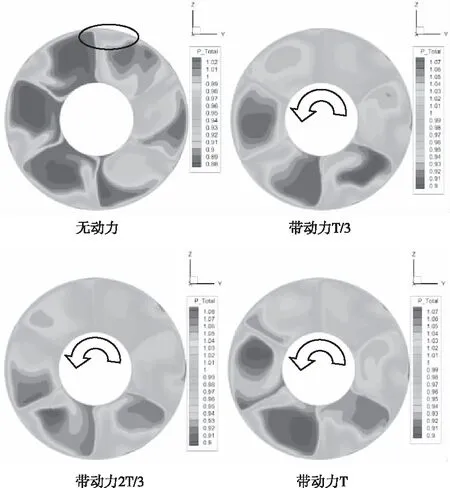
图10 M=0.18,a=15°,进气道出口截面上的总压恢复系数图谱
4.3 侧滑状态下的双发滑流影响对比
侧滑状态下(计算状态4和5)的流场分布如图11和图12所示,在正、负侧滑下,受旋转螺旋桨的影响,左、右发的流场并不是对称分布。从前往后看,螺旋桨为右旋,因此正侧滑时(β=25°),螺旋桨的旋转可抵消部分侧滑角,螺旋桨后的气流局部侧滑角减小;负侧滑时,螺旋桨后的气流局部侧滑角增加。但从表4所示的进气道性能参数上来看,无动力状态下,正、负侧滑下左、右进气道性能基本相当,总压恢复系数为0.96,畸变指数为0.115,主要原因是环形进气道位于螺旋桨根部,螺旋桨根部对前方来流侧滑角的影响量不大,因此左右进气道性能基本没有差别。带动力后,螺旋桨增压作用使进气道总压恢复系数增大约3.3%,使畸变指数增大约7%,可见,侧滑状态下螺旋桨对进气道畸变的影响相对较大。

图11 b=25°流场分布 图12 b=-25°流场分布
图13和图14给出了正侧滑角时左、右进气道出口面上的图谱(顺航向),双侧进气道图谱基本没有差别,无动力时,右上区域为低能区,带滑流后,低能区扩展为整个上部区域。图15给出了负侧滑角时左侧进气道出口面上的图谱(顺航向),无动力时,右下区域为低能区,带滑流后,低能区向右上区域移动。负侧滑时,图谱相对均匀,畸变比正侧滑时低1%左右,可见,正侧滑状态下滑流对进气道性能的影响略大些。
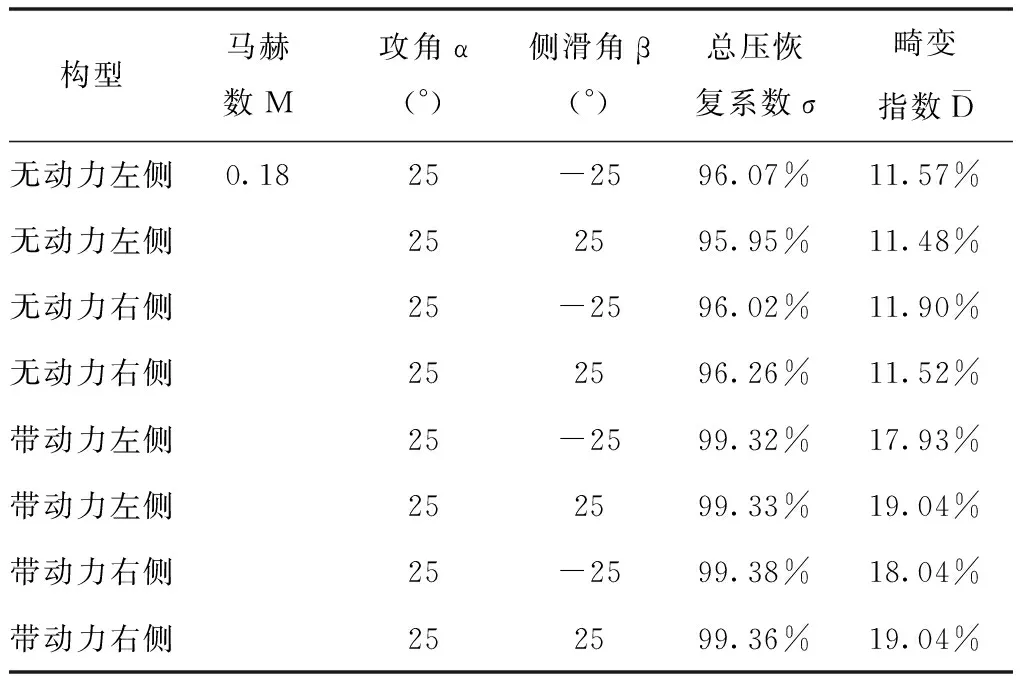
表4 进气道的总压恢复系数和畸变指数对比结果(带侧滑)

图13 M=0.18,a=25°,b=25°,进气道出口截面上的总压恢复系数图谱(左侧进气道)

图14 M=0.18,a=25°,b=25°,进气道出口截面上的总压恢复系数图谱(右侧进气道)
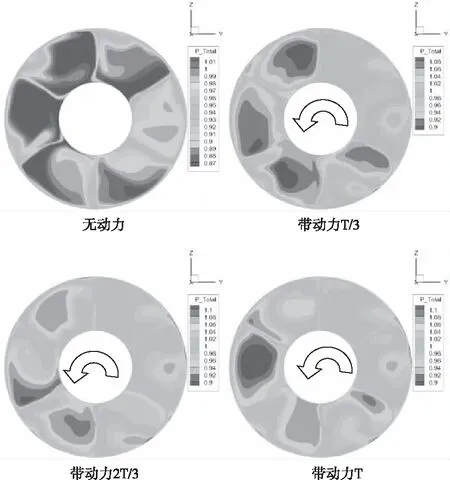
图15 M=0.18,a=25°,b=-25°,进气道出口截面上的总压恢复系数图谱(左侧进气道)
5 结论
本文对一种位于螺旋桨根部的环形进气道性能进行了数值仿真,螺旋桨滑流影响下,该进气道的总压恢复系数和畸变指数发生了显著变化,具体表现为:
1) 地面静态时,唇口绕流为主要形态,滑流影响相对最小,螺旋桨增压作用使总压恢复系数增大约1.4%,畸变指数增大约2%;
2) 带风速状态下,前方来流绕过螺旋桨叶片根部,拉起低能流,滑流影响增强,使总压恢复系数增大约3%,畸变指数增大约4%-5%;
3) 侧滑状态下,机身对双侧进气道的性能影响不大,滑流影响最为显著,使总压恢复系数增大约3.3%,畸变指数增大约7%,负侧滑状态下的畸变略小于正侧滑状态。
