某航天器转载过程中瞬态碰撞动力学研究

郭君斌，于传强，王俊提，高 杨

(1. 火箭军工程大学，陕西 西安 710025；2. 火箭军装备部驻长治地区军事代表室，山西 长治 046012)

1 引言

“航天器-适配器-运输筒”系统在转载运输过程中发生碰撞的概率非常小，但也难免由于操作失误或者操作不当而发生碰撞，而碰撞又直接关系到航天器内部精密仪器的可靠性问题，因此作为系统整体被动安全性的重要内容之一，对于在运输过程中产生的碰撞以及振动问题，如何降低损害是航天器亟待解决的关键问题之一。

航天器在运输过程中涉及的结构主要包括运输筒、适配器等部分。其中，运输筒材质主要以高硬度玻璃钢为主，起保护、定位、支承航天器以及保温的作用。适配器的材质是粘弹性阻尼材料，以聚氨酯泡沫塑料为主体，在内表面布置粘贴海绵橡胶层，在外表面粘贴聚四氟乙烯薄膜，既能较好的调节航天器的舱体公差，提高适应性，亦可以减小进出筒时与筒间的接触阻力，显著提高系统的阻尼，迅速减弱波在系统中的传播速度，在较短时间内使得系统振动得到迅速衰减，从而起到抑制振动的效果。

解析法、数值法、试验法是研究系统碰撞和振动问题的常用方法。解析法计算量大，求解过程复杂，且多数情况无解，目前有李士军等人运用Blatz-Ko应变能函数，以三次缩减的多项式的形式，得到了系统中轴对称面上的位移和应力、应变解析解；Tzou和Kim对弹性面板以及厚板的面内振动进行解析求解，求解了自由振动的振型和振幅等精确解；Park则以圆板面为对象，研究其自由振动，并利用Helmholtz分解法获得了自由振动方程以及固有频率的精确解；罗忠和李恩奇等人以圆柱壳为研究对象，结合其阻尼特性，用解析法解得其动力学固有特性。试验法通常是消耗性，不可往复使用，成本大、耗时长。数值法一般采用有限元法，是一种工程上常用的数值仿真方法，且发现问题可以及时修改模型重新仿真，因此是系统结构设计过程中碰撞安全性结构设计与分析的主要方法。

本文围绕运输过程中的“航天器-适配器-运输筒”系统，利用瞬态动力学理论和有限元数值仿真分析方法，主要研究“航天器-适配器-运输筒”系统在运输过程瞬态碰撞的动力学响应以及适配器在碰撞过程中的减振效能。考虑运输筒和航天器的弹性变形，利用有限元数值仿真软件ABAQUS建立多刚柔耦合体系统动力学模型，并分别对舱体、适配器和运输筒进行刚柔耦合分析，以数值法模拟系统在三种不同停放方式下的碰撞过程，计算航天器系统三种不同停放方式下的动力学响应，得出系统关键节点处的位移、速度、加速度等运动响应特性曲线，最后研究减振装置适配器在碰撞过程中的减振效能。

2 结构模型

航天器在运输中采用的系统结构形式如图1所示。在“航天器-适配器-运输筒”系统中，适配器和运输筒结构相对简单，质量分布均匀，但航天器上包含设备较多，与适配器和运输筒相比，结构也比较复杂，利用质量密度线性分布假设，首先确定航天器舱段数以及各个舱段的质心位置和各个舱段质量，建立航天器模型。模型采用8个舱段，如图2所示，各舱段等效壁厚分别为22 mm、20 mm、45 mm、14 mm、62 mm、18 mm、66 mm和12 mm。“航天器-适配器-运输筒”系统的三维结构模型如图3所示，相应的材料参数如表1所示。

图1 “航天器-适配器-运输筒”系统动力学模型

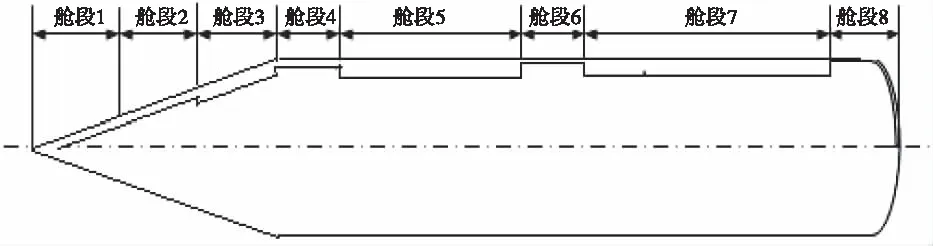
图2 航天器各舱段结构分布简图

图3 “航天器-适配器-运输筒”系统的三维结构模型

表1 材料参数

3 仿真模型

3.1 网格模型

在有限元分析中，网格划分的类型和网格质量是关键因素，“航天器-适配器-运输筒”系统模型网格划分过程中，由于结构相对复杂，各个舱段的壁厚、形状、材料不尽相同，都增加了网格划分的难度，因此，默认的网格划分技术无法自动生成规则网格，需要进行手动划分。根据航天器的等效结构，将航天器依据舱段位置划分为8个区域以扫描技术进阶算法进行网格划分，构建结构化网格或扫描网格。网格尺寸大小为0.05，网格类型为八节点线性六面体单元，网格数量为27921，节点数为35264。与之相对的，在运输筒和适配器模型的网格划分中，网格划分算法、网格尺寸、类型与航天器一致，得到运输筒网格数10265，单元节点数21395，适配器网格数2136，单元节点数3471。网格模型如图4所示。

图4 “航天器-适配器-运输筒”系统结构网格图

3.2 碰撞载荷施加

“航天器-适配器-运输筒”系统被放置于运输车或放置于工作车上时，速度瞬间减小并趋近于零。由于惯性作用，系统会产生加速度，此加速度值的大小由转载放置距离、所用时间、初始状态共同决定，放置、运输时速度越大，放置过程时间越短，那么惯性加速度就越大，且航天器质量较大，相应的惯性力比较大。在动力学分析中，将此加速度等效为系统的前后支承位置同时受加载时间为0.2s、幅值为16kN的集中力作用。而转放安置设备将系统放到运输车上时通常又会出现三种停放方式，方式A：运输筒前后支点同时接触；方式B：运输筒前支点先于后支点接触；方式C：运输筒后支点先于前支点接触。这三种方式等效瞬态载荷加载情况如图5-图7所示。

图5 方式A载荷时间历程

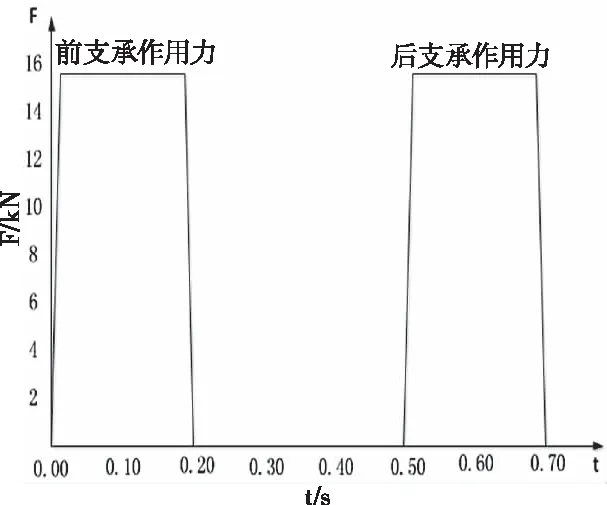
图6 方式B载荷时间历程

图7 方式C载荷时间历程

4 仿真结果分析

4.1 航天器关键节点瞬态碰撞动力学分析

利用有限元数值仿真软件ABAQUS中的模态分析模块对系统三种不同停放方式进行振动分析，对系统结构停放方式A、B、C分别做瞬态碰撞响应计算。图8-图10和图11-图13分别绘制了航天器两个典型位置(航天器舱头位置位于舱段1的节点566处和舱尾位置位于舱段7的节点12820处)的位移、速度、加速度响应结果。

图8 舱段1的节点566处的位移响应

图9 舱段1的节点566处的速度响应

图10 舱段1的节点566处的加速度响应

图11 舱段7的节点12820处的位移响应

图12 舱段7的节点12820处的速度响应

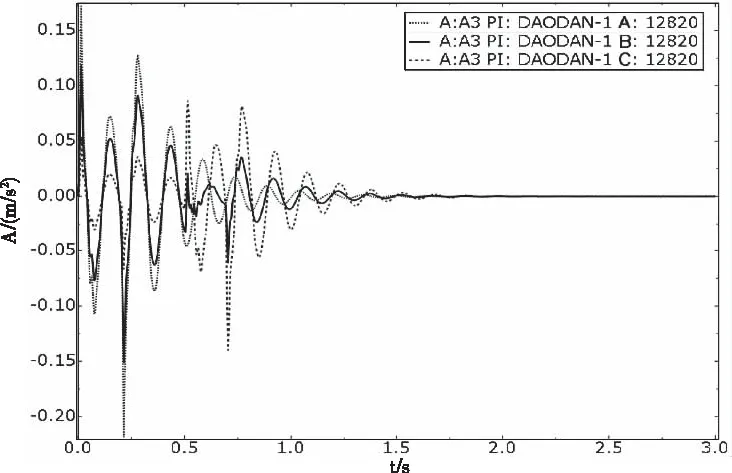
图13 舱段7的节点12820处的加速度响应

通过观察上述三种不同停放方式下航天器舱头和舱尾的瞬态碰撞位移、速度、加速度响应曲线图可以得到如下结论：

1)对于不同停放方式，系统可产生不同的碰撞响应。对于停放方式A，即运输筒前后支点同时接触运输车的情况，系统的瞬态位移、速度、加速度最大；对于停放方式C，即运输筒后支点先于前支点接触运输车的情况，系统的瞬态位移、速度、加速度最小；对于停放方式B，即运输筒前支点先于后支点接触运输车的情况，系统的瞬态位移、速度、加速度响应值介于停放方式A和停放方式C之间。因此，运输筒后支点先于前支点接触运输车的停放方式C最为安全可靠。

2)结构阻尼相同时，系统的瞬态位移、速度、加速度衰减速度最快的是运输筒前后支点同时接触运输车的停放方式A，其次是运输筒前支点先于后支点接触运输车的停放方式B，衰减速度最慢的是运输筒后支点先于前支点接触运输车的停放方式C。

3)同一停放方式下，航天器舱头的位移、速度、加速度响应幅值要大于航天器舱尾。

4.2 适配器减振效能评价

适配器在航天器和运输筒之间主要起减振器作用，即可以衰减振动，振动衰减的效果如何，可以用加速度传递率来衡量。加速度传递率的大小指示该区域内加速度的变化，定义为该频段内系统模型中振动的上下参考点的加速度最大值的比值。传递率数值越低，表明减振器系统的减振性能越好，其形式可以具体用分贝来描述，具体描述为

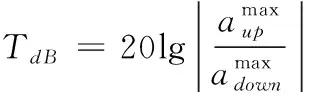
(1)

图14 适配器安装位置

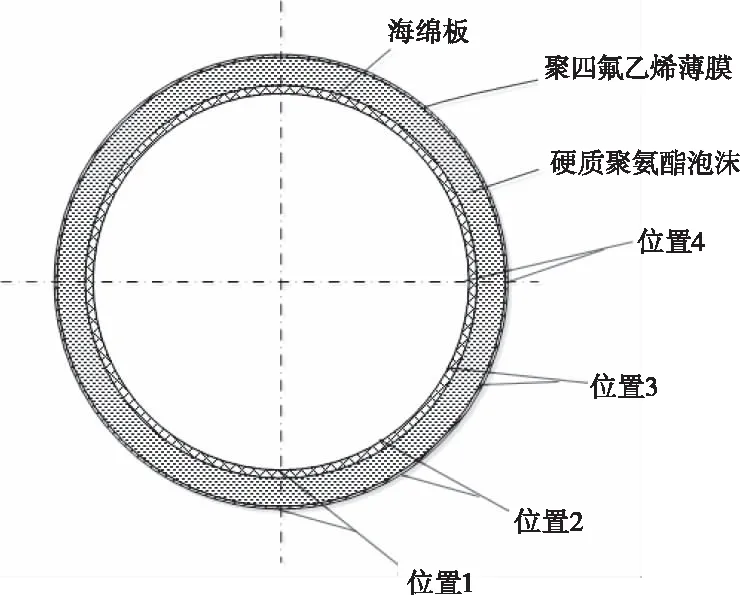
图15 适配器结构简图及关键点位置

以运输筒前后支点同时接触运输车(即停放方式

A

)为分析对象，分别选取图14所示前后适配器，取图15所示最底部位置1向上30°、位置2向上60°、位置3以及水平位置4，求得对应的航天器和运输筒的不同位置处空间最大加速度幅值与传递率，如表2和表3所示。

表2 前端适配器不同位置处上下加速度与传递率

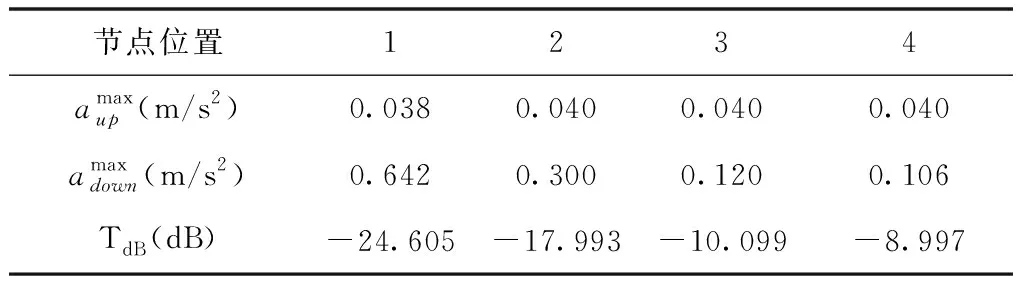
表3 后端适配器不同位置处上下加速度与传递率

从表2及表3可以看出，前端适配器加速度传递率分布在-12.644dB～-5.631dB范围内，后端适配器加速度传递率分布在-24.605dB～-8.997dB范围内。同时，分析表明：

1)航天器轴线方向同一截面上响应加速度一致，且后端适配器的加速度传递率小于前端适配器的加速度传递率，表明后端适配器隔振性能优于前端适配器。

2)沿着适配器最底部往水平方向，加速度传递率呈现增大趋势，表明最底部的隔振性能最好。

3)根据文献[17]提供的常见产品的振动脆值，航天器在该瞬时冲击力下的最大加速度峰值为0.4G，远小于文献中高级精密电子仪器的振动脆值，因此该碰撞对航天器的损害很小，安全性较好。

5 结论

本文结合瞬态动力学理论和有限元数值仿真方法，利用有限元数值仿真分析软件ABAQUS，对转载过程中的“航天器-适配器-运输筒”系统进行了瞬态动力学分析，研究表明：

1)运输筒后支点先于前支点碰撞接触的放置方式最安全，前后支点同时碰撞接触的振动衰减速度最快，且航天器舱头位置的振动响应最大。

2)航天器轴线方向同一截面上响应加速度一致，且后端适配器加速度传递率大于前端，适配器最底部位置隔振性能最好。

3)运输筒后支点先于前支点碰撞接触时，产生的碰撞力对航天器的损害很小，安全性较好。