磁偶极子阵列模型的适用性研究与优化分析*

刘芙妍 颜冰

1) (湖南大学数学学院,长沙 410082)

2) (国防科技大学气象海洋学院,长沙 410073)

随着我国水下探测、通信技术的发展,传统的磁性测量模型已无法满足高精度、高效率建模的需要.本文从舰船磁场积分模型出发,综合分析模型离散化为磁偶极子阵列模型产生的复化中矩形,以及Gauss-Legendre积分余项分析过程引起的离散误差、算法误差,模型简化产生的拟合误差、模型误差等,对模型适用性条件进行分析;同时,以建模精度和计算复杂度为目标构造多目标优化函数,通过NSGA-II 算法对多目标函数进行求解,得到使精度、复杂度较为均衡的最优解集,提出了不同精度、复杂度需求下的选择规则.为了保证结果的有效性,在舰船磁场混合模型的基础上利用数值实验对模型进行验证,充分考虑模型拟合误差,通过对磁性均匀、磁性不均匀潜艇的仿真分析得到模型达到适用范围时距离与磁偶极子数目的相关关系;在保证模型适用的条件下,基于NSGA-II 算法的多目标优化过程所得结果运算效率、精度高,具有很好的工程应用价值.

1 引言

随着潜艇静音技术的飞速发展,传统的声呐探测已无法满足我国水下探测、反潜的需要,为了提高潜艇水下探测能力,磁异常探测已成为水下目标探测的重要手段[1,2].磁异常探测轻便易行、效率高、隐蔽性能好、抗干扰强,具有极高的军事意义和民用价值.为了提高水下探测、反潜能力,建立高精度的磁场模型,提高模型计算效率是重中之重[3].

目前,主要的舰船磁场建模方法主要有两类:一类是由理论推导得到的,如大平面法、边界元法、有限元法等,这类方法计算精度高,但测量要求高,无法满足实际工程需要;另一类是磁体模拟法,将舰船等效为磁偶极子阵列模型,利用其模拟舰船的局部磁场.其中,磁体模拟法可以在少量的磁场测量数据下完成精度较高的舰船磁场建模[4],应用广泛.如生成海洋军事武器物理磁场模型,全面监控水下移动电磁目标[5];水下移动电子装置的识别、追踪拦截[6];地磁勘探和探测、确定未爆炸物[7,8];建立水雷全型号电磁分布模型[9,10];探测几百米外远处的潜艇[11]等.海洋探测、通信等技术的发展,对磁性测量的精确度提出了更高的要求,但磁偶极子阵列模型中磁偶极子数目、分布以及适应性条件等对磁体磁场分布等效效果的影响尚无较为系统的研究和成熟的理论[12,13].

对于磁偶极子模型的高精度高效率计算问题,Lutkenhoner[14]通过数值实验验证了单磁偶极子转化为两个磁偶极子的可行性,探索了成功分离两个偶极子的最低要求;吴旭东等[15]最早讨论了磁偶极子标量模型的推导以及理想磁偶极子成立条件;牛龙飞等[16]提出3 个磁偶极子对舰船磁场进行建模,在不显著增加复杂度的情况下增加了真精度;Lucas 和Richards[17]以及 Nilsson[18]提出磁偶极子阵列可以被视为船舶产生的磁场源,提出船舶磁化范围的各种模型.戴忠华等[19]在阵列模型计算磁场分布的情况下,利用单磁偶极子反演推算得到磁矩收敛性,得出在2.5 倍距离外将水下目标等效为单磁偶极子模型时具有较高精度的结论,这一结论的提出为舰船单偶极子模型的应用提供了依据,但仅适用于单磁偶极子,证明过程依赖阵列模型的准确性;金煌煌等[13]研究了利用多磁偶极子模型等效模拟磁异常目标空间磁场分布时,在不同空间尺度条件下的多磁偶极子磁矩、空间分布对等效效果的影响即多磁偶极子等效规律.但利用混合模型进行适用性研究的过程大都利用单磁偶极子与阵列模型之间的等价性,忽视了模型建立过程产生的误差;而磁偶极子个数的选取过程中较少对计算复杂度进行考虑,往往会造成磁偶极子数过少模型精度较差、数目多计算复杂度高等问题,使模型的适用性较差.

本文从舰船磁场混合模型的相关理论出发,提出了基于复化中矩形、Gauss-Legendre 法余项的阵列模型的适用性研究,通过对积分模型离散化为阵列模型产生的积分余项及余项估计过程产生的离散误差及磁体模拟法产生的拟合误差、算法误差、磁偶极子距离数目差异引起的模型误差进行综合分析,讨论模型的精度,提出了磁偶极子模型的适用性条件;同时,基于模型误差与参数的相关性,以建模精度和计算复杂度为目标构建多目标问题,通过对多目标函数的求解得到使精度、计算量较为均衡的磁偶极子数,实现了模型的高精度、高效率计算.所提出的方法以国外某潜艇进行仿真验证,从计算精度、效率、模型适用性等方面对模型进行分析,结果表明该模型可以显著提高磁场精度和计算效率,具有重要的理论意义和实用价值.本文第2节探究了磁场积分模型离散化为磁偶极子模型的过程;第3 节基于复化中矩形、Gauss-Legendre 数值积分法综合考虑离散误差、模型误差、算法误差对磁偶极子模型的适用性条件,进行了对比分析;第4 节通过磁性分布均匀、磁性分布不均舰艇的仿真计算及模型拟合误差得到了磁偶极子模型的适用性条件;第5 节利用多目标函数优化算法对多目标问题进行求解,提出一种高精度、低复杂度的舰船磁场建模方法.最后对实验结论进行了总结分析.

2 磁偶极子积分模型离散化

积分方程法、微分方程法是电磁场数值计算的重要方法.目前国内外有关电磁场数值计算的著作大多偏重于微分方法求解二维磁场问题,而在许多实际场问题的计算中,尤其是在计算三维场时,需要采用积分方法或者积分-微分混合方法,才能达到较高精度[20].电磁场可以用麦克斯韦方程组描述,对麦克斯韦方程组积分得电磁场积分形式的解,以这些解为基础可形成电磁场的积分方程[21]:

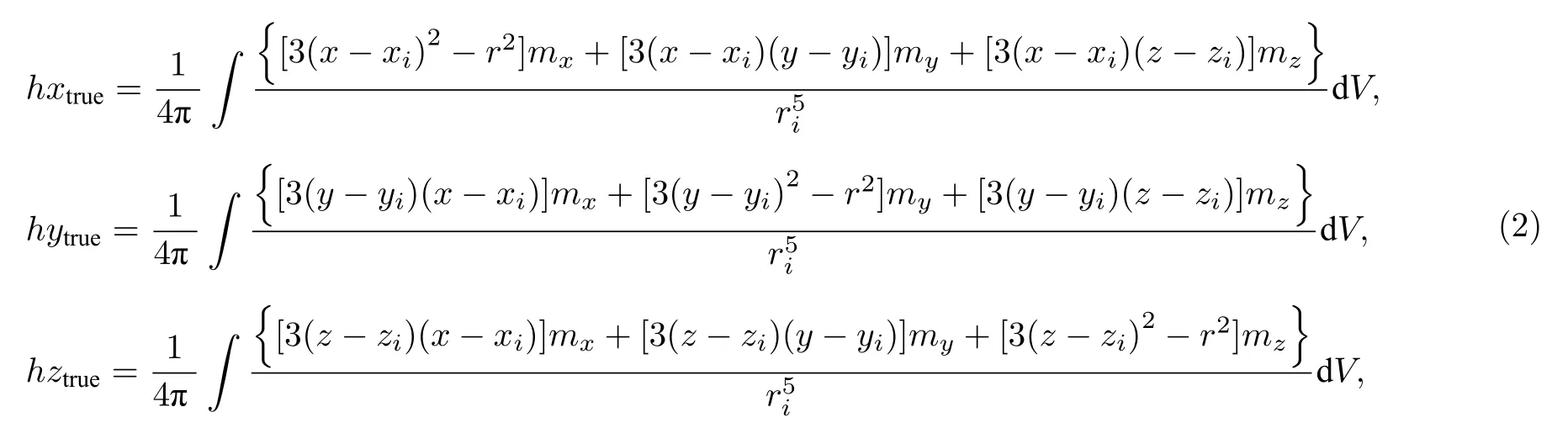
利用积分、微分方程对磁场求解的过程,除非场域极其简单否则无法得到解析表达式,但应用数值计算却可以计算大量的数值问题.数值计算的关键在于把求解对象所在区域进行离散化,即通过互不重叠顶点边界相连的有限个单元的总和来对连续场域进行等价[22].由于分子尺度在连续介质理论中相对于连续介质微元总可以认定为充分小量,假定将磁源分割为n个小磁体,小磁体中心点坐标分别为 (xi,yi,zi),i1,2,···,n,观测点坐标为(x,y,z)处的数值磁场强度 (hxsim,hysim,hzsim),则可得磁场强度离散化模型,即磁偶极子阵列模型[19]:

对积分模型(2)、磁偶极子模型(3)进行简化,假设磁源为磁性均匀各向同性的立方体,可得mxdVmydVmzdVmdV,m为常数,取观测点坐标为 (0,0,0) ,磁偶极子中心点坐标 (x,y,z),得磁偶极子x轴方向的磁场强度简化积分模型为

(4)式的被积函数为

简化后x轴方向磁偶极子模型为

其中mi表示第i个小磁体的磁矩.

积分模型(4)式可以得到的磁源在观测点磁场强度较为精确,但利用微积分基本定理求解存在无法找到原函数、原函数复杂、被积函数没有有限的积分表达式等问题,因此在实际应用中常常采用数值积分方法对多重积分进行估计.磁偶极子模型是积分模型离散化的结果,一般情况下磁偶极子数量越多,对测量点上磁场的拟合精度越高,此外,拟合的精度高低还与磁偶极子的分布有关.因此研究模型适用性需要具体分析的误差包括:模型在离散化过程中产生的误差,即积分余项无法精确计算得到,此时该误差可归入离散误差;磁测物体磁场较为复杂,无法用一个简单的解析式计算,因此采用已知磁场分布的磁性物体来等效实际潜艇带来的模型拟合误差;在计算过程中由于数值分析方法选择的差异产生算法误差;模型在离散化过程中的分布、数目上的差异产生的模型误差;理论分析部分对模型进行一些简化及算法运行过程中产生的舍入误差相对其他误差影响较少,不做过多的分析.

3 磁偶极子模型适用性

通过理论分析积分余项来研究模型适用性的过程,综合考虑了复化中矩形算法、Gauss-Legendre算法的对比分析及磁偶极子数目位置的差异等引起的算法误差、离散误差及模型误差等.

3.1 复化中矩形法余项

多重积分的求解是工程研究中常见的问题,多重积分的复化中矩形法,就是将多重积分转换成多次的定积分,在每重积分计算时用复化中矩形公式对积分进行估计,最后得到多重积分近似值的方法[22].磁偶极子模型为立体空间中的三维模型,因此首先利用复化中矩形公式三重积分余项估计对(4)式的截断误差进行分析,设f(x)在区间[a1,b1]×[a2,b2]×[a3,b3]上连续、可微,得到如下三重积分问题:

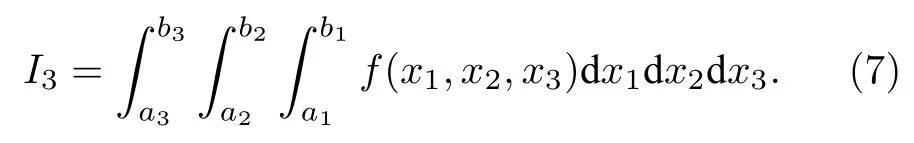
利用复化中矩形法对多重积分(7)式进行数值计算得I3:

3.2 Gauss-Legendre 余项

复化中矩形法是常用的一种有效算法,它突出的优点是计算过程简单,可以很好地在工程中推广应用.与复化中矩形法相比,Gauss-Legendre 法在节点数一定的情况下具有更高的代数精度和收敛性.为了更好地对磁偶极子积分模型离散化误差进行分析,利用Gauss-Legendre 余项估计对多重积分(7)式进行数值计算得:

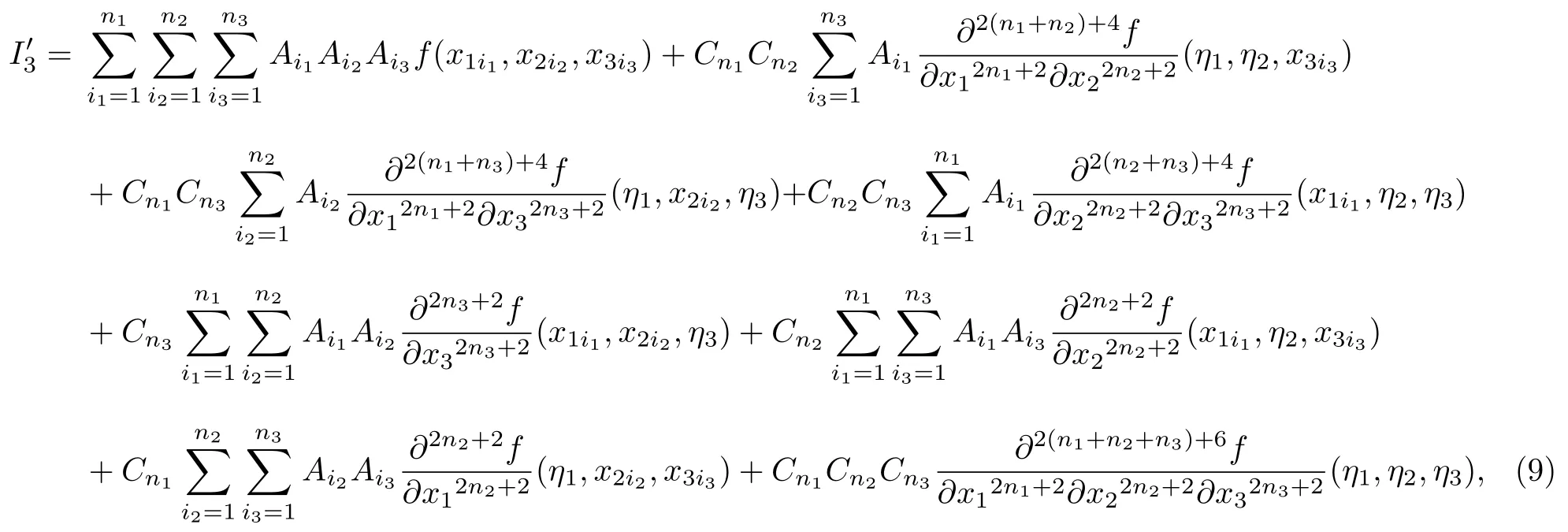
3.3 磁偶极子模型误差

通过积分余项可以对模型误差进行有效估计,得到磁偶极子模型误差的解析解.利用(8)式得(4)式磁偶极子积分公式的积分余项.考虑到η的精确求解较为复杂,为提高计算精度,降低复杂度,分别对单磁偶极子条件下η趋近于均值、最大值、最小值、中值及最大最小值与中间值内部,即等的取值情况进行讨论,得到不同条件下模型实际误差与余项不同取值情况下产生的取值误差之间的相对误差,结果如图1 所示.可以看出,当η取均值时其产生的舍入误差相对较小且最稳定,因此选择η取均值情况下的取值误差及截断误差带来的离散误差对模型进行接下来的讨论.

图1 单磁偶极子条件下相对误差随 η 的变化Fig.1.Relative error as a function of η for a magnetic dipole.

当E≤6% 时磁偶极子模型能够有效对磁源进行建模,当E≤3% 时磁偶极子模型的建模精度较高,能够有效地在相关工程中应用[4].

(10)式给出了求磁偶极子相对误差的具体方法,接下来对距离、磁偶极子数目的差异产生的模型误差进行分析.当磁源为立方体时,分别对磁偶极子数目1—4,磁源与观测点距离为1—3 倍立方边长的情况进行分析,得到基于磁偶极子阵列模型的不同距离及磁偶极子数目的磁场相对误差,结果如图2 所示.可以看出:随着距离的增大,模型相对误差趋于收敛,单磁偶极子在1.8 倍距离处趋于稳定,相对误差为5.9%,达到了有效建模距离;随着磁偶极子数目的增多,模型的相对误差逐渐减小,在2 个磁偶极子时模型在1.3 倍距离处就达到了2%的相对误差,达到了较高的模型精度.

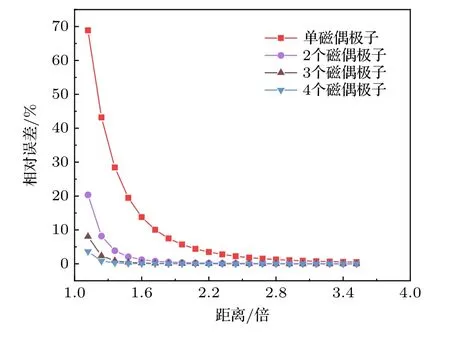
图2 基于复化中矩形法模型误差随距离及磁偶极子数目的变化规律Fig.2.Variation of model error with distance and the number of magnetic dipoles based on composite middle rectangular method.

同理得基于Gauss-Legendre 法的磁偶极子阵列模型的不同距离及磁偶极子数目的磁场相对误差,结果如图3 所示.可以看出,在Gauss-Legendre法下单磁偶极子在1.5 倍距离处趋于稳定,相对误差为5.05%,达到了有效建模距离.与复化中矩形法对比可得,Gauss-Legendre 法对磁偶极子积分模型离散化的过程更易达到有效建模距离,该方法得到的磁偶极子阵列模型对磁偶极子分布的位置与磁偶极子所占的比例进行了规划,较复化中矩形法更为合理.由于理论分析过程存在较多简化,如将磁体假设为磁性均匀各向同性的立方体、积分余项简化取均值等,与实际情况存在一定差距,接下来利用数值例子对上述方法进行检验.

图3 基于Gauss-Legendre 法模型误差随距离及磁偶极子数目的变化规律Fig.3.Variation of model error with distance and the number of magnetic dipoles based on Gauss-Legendre method.

4 数值仿真实验

本数值实验在第3 节的基础上对日本“苍龙”级潜艇进行研究,潜艇艇长80 m,半径5 m,尾部半径2 m,尾部长度15 m.实际应用中,往往需要将空间磁场的分布规律抽象出来,形成一个可快速预测的模型,从而便于利用测量信号进行目标参数识别.因此,基于潜艇的外形特点,有学者提出了等效旋转椭球体模型[23],为了方便计算将其等价为长为80 m,最长半径为5 m 的旋转椭球体,如图4 所示.上述混合椭球体模型采用磁体模拟法,与实际水中磁性目标存在些许差距,但实验表明离开磁性目标的距离在其两倍宽度以上时,旋转椭球体磁场对目标磁场的拟合精度超过85%,为了保证研究的准确性,将该误差作为模型拟合误差代入后续分析过程[24,25].同时跟据潜艇的磁性分布将其分为均匀、不均匀两种情况进行仿真分析.

图4 潜艇模型Fig.4.Submarine model.

4.1 观测点选取

实验时为避免取点不均、取点较少没有代表性带来的偶然误差,利用极坐标求得以(0,0,0)为圆心,以r为半径的球面上均匀分布的N60 个点作为观测点,坐标 (x,y,z) 分别为

图5 r=224 时选取的均匀采样点Fig.5.Uniform sampling points selected when r=224.

4.2 磁性均匀情况

假设潜艇所用材料的磁性是均匀的,即为均匀旋转椭球体.旋转椭球体在均匀磁化时的磁矩等于电流I与最大横截面积S的乘积[26].考虑到旋转椭球体在各个坐标平面上的投影存在差异,根据

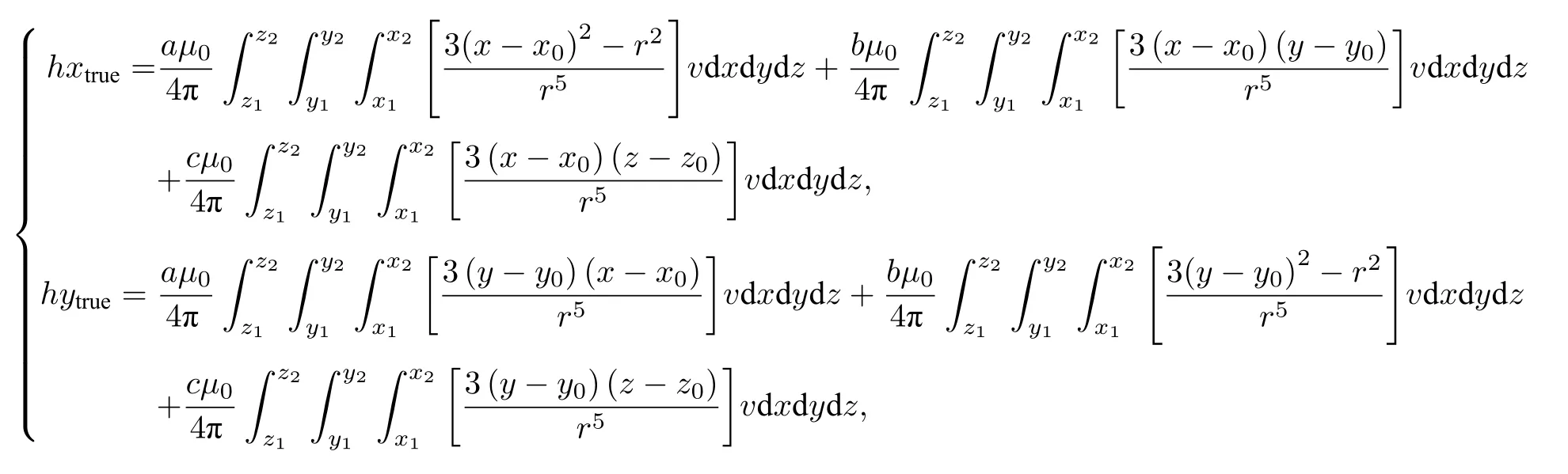
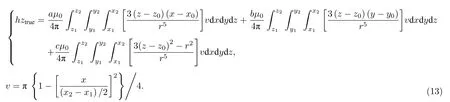
其中 (hx,hy,hz) 为积分模型下目标磁场在各坐标轴上实际磁场强度的投影分量.在磁源取椭球体割块的中心,观测点 (x,y,z) 均匀选取的情况下,由(3)式和(13)式得磁偶极子模型的相对误差:

其中Ej为第j个观测点的相对误差.由(14)式得到模型相对误差随距离及磁偶极子数目的分布情况,如图6 所示,其中不同颜色代表相对误差取值.图6(a)中x,y,z轴对应测量距离、磁偶极子数目、模型相对误差,图6(b)中横纵坐标分别对应测量距离及磁偶极子数目,坐标轴为共用轴.图6(b)中标记线为控制距离或磁偶极子数目,其中一个变量恒定,模型相对误差随另一个变量的变化规律.

图6 磁性均匀时模型相对误差变化趋势 (a)磁偶极子数目、距离对模型误差影响的三维柱状图;(b) 磁偶极子数目、距离对模型误差影响的等高线剖面图Fig.6.Trend of relative error of the model when the magnetic is uniform:(a) Three dimensional histogram of effects of number and distance of magnetic dipoles on model error;(b) contour of effects of number and distance of magnetic dipoles on model error.

1)磁偶极子数目一定时,随着测量点与磁源距离的增大,相对误差逐渐减小并收敛至稳定值,此后增加距离模型相对误差不会产生较大改变,且磁偶极子数目越少相对误差对距离的敏感度越高,如图6(b)中3 个磁偶极子与9 个磁偶极子相比误差随距离的变化更显著.

2)距离一定时,随着磁偶极子数目的增多,相对误差逐渐减少.由图6(a)柱状图的颜色分布可知,在少于5 个磁偶极子时,模型相对误差对距离的敏感性较大,并逐渐达到稳定值;在测量点与磁源距离较近时对磁源进行分割可有效提高磁偶极子模型的适用性,如图6(b)中r=64 比r=204 时误差随磁偶极子数目的变化更显著,磁源的分割次数与模型的复杂度成正相关,增加模型的复杂度在分割次数达到一定程度时并没有显著变化.

假设磁偶极子模型建模有效距离为相对误差≤6%,根据不同距离与磁偶极子数目产生的相对误差,对模型适用性进行分析,计算结果如表1 所列.可以看出:单磁偶极子在r=184 (2.3 倍)时相对误差达到6%的建模有效范围;两个磁偶极子在r=104 (1.3 倍)时相对误差达到有效范围,且两个磁偶极子模型的适用范围相对较大;在距离较近时需要对磁源进行大量的分割,如在1.05 倍距离处需要3 个磁偶极子保证模型的适用性.

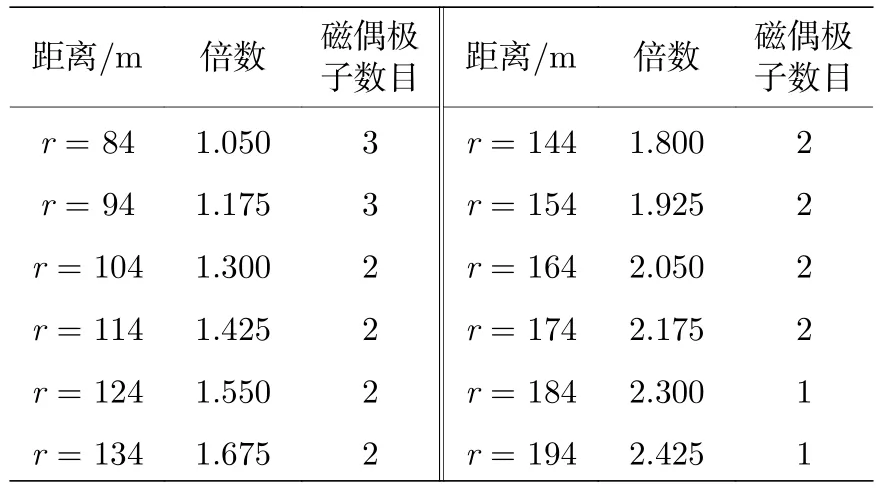
表1 磁性均匀情况下,达到建模有效范围的磁偶极子数目及距离Table 1. Number and distance of magnetic dipoles reaching the modeling effective range when the magnetic is uniform.

4.3 磁性不均匀

假设潜艇材料的磁性是不均匀的,就水平分量而言,通常舰船磁场峰值出现的位置与其所处于的纬度区域无关[27],一般分别在舰首附近、舰船中部、舰尾附近出现峰值,舰船中部可能出现磁场值为0 的情况.为了保证能够充分展现磁偶极子分布不均匀对模型造成的影响,本仿真对潜艇首尾至中部的磁性差异呈线性下降的形式进行了分析[28]:

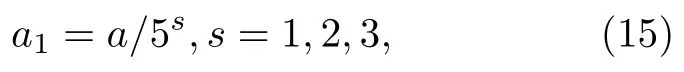
其中a1×106为潜艇首尾两端的常数,a1为潜艇中间常数值.可得磁偶极子积分模型在x轴方向磁场强度为

利用本文第3 节理论得到的磁偶极子模型x方向的磁场强度hxsim,由 (10) 式得相对误差.首先对距离为224 (>2.5 倍)时模型的相对误差进行分析,当两端的磁矩常数a1×106,中部磁矩常数a1分别为200000,40000,8000,即由两端向中心呈线性下降时,相对误差变化趋势如图7 所示.其中图7(a)中不同颜色代表测量距离为224 m 时舰艇磁性的差异,图7(b)中不同颜色代表模型在距离与磁矩存在差异时的相对误差,随着磁偶极子数目的增多、磁性差异的减少,模型相对误差逐渐减少,且相对误差呈现出波动下降的规律.

图7 距离为224 时模型相对误差随潜艇磁性差异的变化趋势 (a)潜艇磁性差异对模型相对误差影响的折线图;(b) 潜艇磁性差异对模型相对误差影响的等高线图Fig.7.Variation trend of model relative error with submarine magnetic difference when r=224:(a) Line graph of the effect of submarine magnetic differences on the relative error of the model;(b) Contour plot of the effect of submarine magnetic differences on the relative error of the model.

接下来对a14×104时的模型相对误差进行分析,结果如图8 所示,其中不同的颜色代表相对误差的差异,图8(b)为图8(a)的投影.图8(b)中的曲线图为距离112 和187,磁偶极子数目为2,6 和12 时,固定一个变量模型相对误差随另一变量的变化趋势.

1)当a14×104,磁偶极子数目一定时,随着测量点与磁源距离变化,相对误差对距离的敏感性较低,如图8(b),距离变化不会造成相对误差较大的波动.

图8 a1=40000 时模型相对误差的变化趋势 (a)磁偶极子数目、距离对模型误差影响的三维柱状图;(b) 磁偶极子数目、距离对模型误差的影响等高线剖面图Fig.8.Tendency of the relative error of the model when a1=40000:(a) Three dimensional histogram of the effect of the number and distance of magnetic dipoles on the model error;(b) contour map of effects of the number and distance of magnetic dipoles on model errors.

2)当a14×104,距离一定时,随着磁偶极子数目的增多,相对误差逐渐减少,当少于4 个磁偶极子时模型相对误差对磁偶极子的敏感性较大,并以波动下降的形式逐渐达到稳定值;随着磁偶极子数目的增多,距离的增大波动逐渐平稳.

对磁性不均匀磁源的磁偶极子模型进行适用性分析,计算结果如表2 所列.可以看出,磁性分布不均时在重心取点的情况下单磁偶极子的相对误差很难达到6%的建模有效范围,且距离增加对模型相对误差的影响较小,更适合通过磁偶极子数量的变化控制其相对误差.

表2 磁性不均匀情况下,达到建模有效范围的磁偶极子数目及距离Table 2. Number and distance of magnetic dipoles reaching modeling effective range when the magnetic is nonuniform.

综合上述仿真可以得到舰艇单磁偶极子模型的适用范围在2.3 倍的潜艇长度,再次验证了2.5 倍距离以外将水下目标等效为单磁偶极子模型具有较高精度的结论.当模型为两个磁偶极子时可以将距离范围缩小为1.3 倍,即距离较近时可以通过增加磁偶极子数目来保证模型的适用性.当磁场不均匀时距离变化对相对误差的影响较磁偶极子数目变化对相对误差的改变要小.因此在磁性不均匀时,Gauss-Legendre 数值积分法离散得到的磁偶极子模型具有更高的稳定性与精确度.

5 潜艇磁场模型的多目标优化

在计算过程中不难发现,随着潜艇分割次数的增加,磁偶极子模型越来越精确,此时模型的计算量也随之增大.因此模型误差及计算量在给定区域内是相互冲突的,不存在唯一最优解,只能通过多目标优化方法进行求解.

传统多目标优化算法是将各目标函数取加权和,将多目标优化问题转化为单目标优化问题,由前文可知,目标函数为建模相对误差及为模型计算量,各目标函数不具备可比性,加权系数难于选择[29].多目标问题中,各目标之间往往是相互冲突的,通常通过决策变量来协调权衡和折中处理,使各子目标函数尽可能达到最优.多目标优化问题不存在单个最优解,而是Pareto 最优解集,它为决策者提供了一个最佳的选择空间,空间内所有解不受Pareto 前沿之外的解支配.如何求得与真实Pareto前沿一致的Pareto 最优解集是多目标函数优化问题的关键[4].

建立变量连续的多目标规划问题

其中x为决策变量,f(x)(f1(x),f2(x),···fm(x))′为目标向量,gi(x),hj(x) 为约束条件[30].首先利用r=234,124 时的数据进行求解,模型的约束条件为模型相对误差<6%,得r=234,124 时决策变量范围分别为X(1){1,2,3,···,16},X(2){3,4,5,···,16}.利用4.2 节计算数据对拟合得到磁偶极子数目与误差的函数,拟合公式为

本实验实际运行时间与磁偶极子数目的拟合结果为

即磁偶极子数目越大模型运行的时间复杂度越大.

建立如下多目标方程组

(20) 式和(21)式为关于潜艇分割规律的多目标最优化问题,接下来研究该问题的求解算法[31].目前基于帕累托最优概念的遗传算法包括:非支配排序遗传算法(NSGA)、带精英策略的非支配排序的遗传算法(NSGA-II)[32,33]等.NSGA 计算复杂度较高、算法的执行速度也较慢;NSGA-II 在NSGA的基础上通过快速非支配排序法,降低了算法的计算复杂度、提出了拥挤度和拥挤度比较算子,代替了需要指定共享半径的适应度共享策略,引入精英策略,扩大采样空间具有很好的适用性,NSGA-II具体步骤[34]包括:

1)对运行参数,交叉率、变异率、交叉分布指数、变异分布指数进行初始化,在解空间内随机生成个体数为N的初始种群Pt,t=0,并将其作为父代种群;

2)父代种群Pt进行二元竞赛选择、模拟二进制交叉、多项式变异操作,产生种群Qt,并将Qt作为子代种群;

3)将Pt和Qt融合在一起,作为规模为2N的临时种群Rt,对其进行快速非支配排序和拥挤度计算,根据个体的非支配排序分层序号和个体的拥挤距离选择出最优的N个个体作为下一代进化操作中的父代种群Pt,t=t+1;

4)判断迭代次数是否等于预设上限值,如果等于则结束运行,否则跳转到第2)步.

已知X(1){1,2,3,···,16},X(2){3,4,5,···,16},参数选择如下:最优前端个体系数为0.3,种群大小为100,最大遗传代数为200,停止代数为200,适应度函数偏差为1×10–100,得Pareto 前沿.

按照实验参数,利用r=234,124 距离处的拟合方程,得到图9 所示的帕累托最优解集,横纵坐标分别为对模型相对误差和运算时间.从图9 可以看出,随着磁偶极子数目的增多,对应的 Pareto最优集的建模拟合相对误差整体减少,计算量整体增大,取误差与计算量的折中数据,即运行时间在t1∈[0.3,1],t2∈[1,2.7]范围内,磁偶极子数为N1∈[3,6],N2∈[7,12] ,相对误差为E1[0.25%,0.5%],E2[0.4%,0.8%],若要尽可能小地减少相对误差,可选择Pareto 前沿中刚处于平衡处的点,可以保证误差较小的同时尽量减少运行时间.接下来对不同距离处的时间与模型相对误差的最优解进行分析,结果如表3 所列.可以看出,当r=124 时磁偶极子数目为8,模型相对误差为0.60%;当r=300时磁偶极子数目为5,模型相对误差为0.30%.可以得到当距离较近时模型不易达到稳定点,随着测量距离的逐渐增大,模型时间复杂度与模型误差达到稳定的数值逐渐减少,且相对磁偶极子数目逐渐稳定.在距离较远、对误差要求较高时,如需考虑时间复杂度,可将磁偶极子数目控制在5 个以内,可以达到二者的相对最优解.

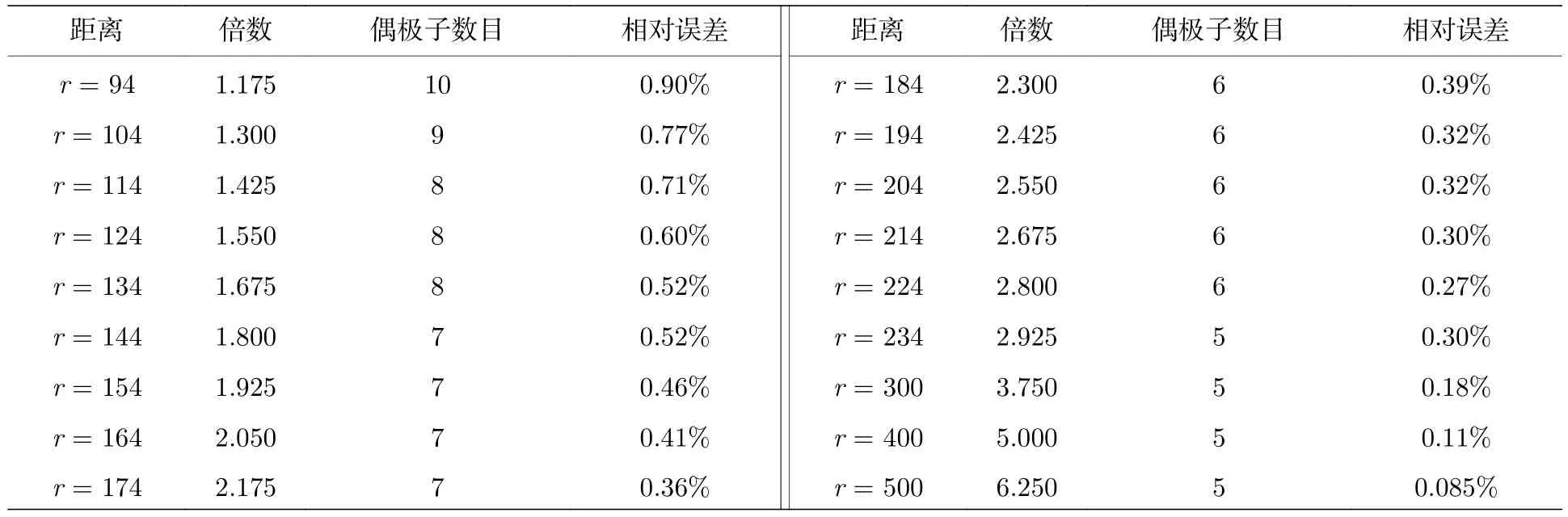
表3 平衡点附近磁偶极子数目及相对误差值Table 3. Number of magnetic dipoles near equilibrium point and relative error.

图9 (a) r=234 和(b) r=124 时Pareto 前沿Fig.9.Pareto front for (a) r=234 and (b) r=124.

该模型能够有效地维护群体多样性,当不同的实验要求对目标偏重有所不同时,此方法可求解得到多个关于显著差别的精度与效率的最终解,提供了多个具有较大差异的选择方案;模型具有较好的收敛性,最终解可以较好地接近帕累托前沿,保证了所求解的真实性.

6 结论

本文围绕磁偶极子阵列模型的适用性、实现潜艇磁场高精度高效率建模的目的进行研究.在对磁偶极子阵列模型的研究中,通过连续模型离散化产生的余项公式对阵列模型误差及磁体模拟法产生的拟合误差、算法误差、磁偶极子距离数目差异引起的模型误差进行分析,来研究模型的适用性条件.首先利用复化中矩形公式法、Gauss-Legendre法对磁偶极子阵列模型余项进行推导,并通过余项估算及模型求解过程中产生的一系列误差对磁偶极子模型的适用进行分析,积分余项即为数值积分产生的截断误差,可归结为离散误差.通过与复化中矩形法对比得到 Gauss-Legendre 法在对磁偶极子积分模型离散化的过程更易达到有效建模距离,该方法得到的磁偶极子阵列模型对磁偶极子分布的位置与磁偶极子所占的比例进行了规划,较复化中矩形法更为合理.

同时对模型误差进行分析,根据磁偶极子阵列模型、积分模型,得到不同距离、不同磁偶极子数目的磁偶极子阵列模型的相对误差及其收敛性.得到磁偶极子模型的适用范围,其中在>2.3 倍潜艇距离外将磁性均匀潜艇等价为单磁偶极子模型具有较高的精度,当距离较近时需对模型进行分割从而达到模型的适用范围.在求解过程中此方法表现出了很强的简便性与适用性.

考虑到潜艇磁性中部与尾部存在较大差异,为充分展现磁偶极子分布不均匀对模型造成的影响,对潜艇首尾至中部的磁性差异呈线性下降的形式进行了分析,发现不均匀潜艇求解过程中增加磁偶极子数目可以有效提高模型精度,且重心的选取尤为重要.

为实现潜艇磁场高精度高效率建模,在充分考虑建模的相对误差与磁偶极子数目基础上构造多目标函数优化模型,通过NSGA-II 算法提出了建模相对误差小于6%的精度与运算效率的相对最优解,仿真分析结果表明该方法能较快地对实验数据进行分析,得到符合人们需求的最佳磁偶极子数目,能够有效地在实际工程中应用.