单层二维量子自旋霍尔绝缘体1T′-WTe2 研究进展*

贾亮广 刘猛 陈瑶瑶 张钰 王业亮

(北京理工大学集成电路与电子学院,低维量子结构与器件工信部重点实验室,北京 100081)

量子自旋霍尔效应通常存在于二维拓扑绝缘体中,其具有受拓扑保护的无耗散螺旋边界态.2014 年,理论预言单层1T' 相过渡金属硫族化合物是一类新型的二维量子自旋霍尔绝缘体.其中,以单层1T'-WTe2 为代表的材料体系具有原子结构稳定、体带隙显著、拓扑性质易于调控等许多独特的优势,对低功耗自旋电子器件的发展具有重要的意义.本文总结了单层1T'-WTe2 在实验上的最新进展,包括基于分子束外延生长的材料制备,螺旋边界态的探测及其对磁场的响应,掺杂、应力等手段在单层1T'-WTe2 中诱导出的新奇量子物态等.也对单层1T'-WTe2 未来可能的应用前景进行了展望.

1 引言

量子自旋霍尔效应是凝聚态物理领域中最基本的量子效应之一,对低功耗自旋电子器件的发展具有重要的意义.量子自旋霍尔效应通常存在于二维拓扑绝缘体中,表现为绝缘的二维体态和导电的一维螺旋边界态[1−6].在无外加磁场的情况下,量子自旋霍尔效应中受拓扑保护的电子可以沿着二维材料的边缘做无耗散运动,且自旋-轨道耦合效应导致不同自旋电子的运动方向相反(图1).

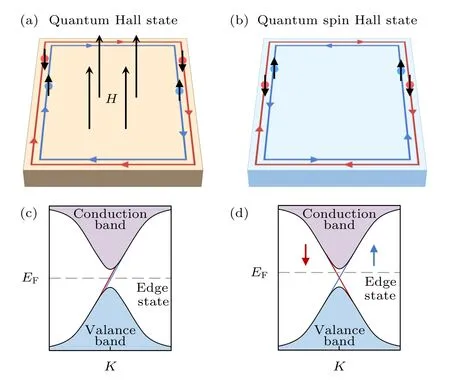
图1 量子霍尔效应和量子自旋霍尔效应的边界态和能带结构示意图Fig.1.Schematic of edge states and band structures in quantum Hall effect and quantum spin Hall effect.

2006 年,美国斯坦福大学Zhang 研究组[7]预言在半导体异质结HgTe/CdTe 量子阱体系中存在量子自旋霍尔效应,并于2007 年被德国维尔茨堡大学物理研究所 Molenkamp 研究组[8]的实验证实,这也是实验上第一个真正实现量子自旋霍尔效应的体系.随后,科学家们在InAs/GaSb[9−12]和InAs/GaInSb[13,14]等量子阱体系中也观测到了量子自旋霍尔效应,但是所需的环境温度通常要远低于液氦温度,这极大地限制了其在自旋电子器件中的应用.基于此,科学家们致力于寻找能够面向未来应用的高温二维量子自旋霍尔绝缘体材料.2014 年,美国麻省理工学院Qian 等[15]预言,以单层1T'-WTe2为代表的单层1T'相过渡金属硫族化合物(transition metal dichalcogenides;TMD)有望成为一类新型的二维量子自旋霍尔绝缘体.其中,单层1T'-WTe2由于具有易于制备、原子结构稳定、体带隙显著、拓扑性质易于调控等许多独特的优势[16−26],引起了实验科学家们的广泛关注.

目前,单层1T'-WTe2已经成为实验性能最好的二维量子自旋霍尔绝缘体之一,其螺旋边界态和量子化的边界电导已被角分辨光电子能谱(angleresolved photoemission spectroscopy,ARPES)、扫描隧道显微镜/扫描隧道谱(scanning tunneling microscopy/spectroscopy,STM/STS)、微波阻抗显微镜(microwave impedance microscopy,MIM)、电荷输运等实验手段相继证实,且其量子自旋霍尔效应在100 K 的温度下仍可稳定存在[17,27−35].此外,利用掺杂、应力等手段可以在单层1T'-WTe2中诱导出包括超导在内的更多新奇量子物态[36−38].因此,对单层1T'-WTe2的可控制备和物性研究不仅能够加深我们对二维量子自旋霍尔绝缘体中新奇量子物态的认识与理解,而且对未来新型自旋电子器件的发展具有重要的推动作用.

本文主要综述了单层1T'-WTe2这一新型二维量子自旋霍尔绝缘体在实验上的最新进展,包括基于分子束外延技术(molecular beam epitaxy;MBE)生长的单层1T'-WTe2制备方法,单层1T'-WTe2中二维量子自旋霍尔绝缘体的探测及调控(图2),并对单层1T'-WTe2未来可能的应用前景进行了展望.

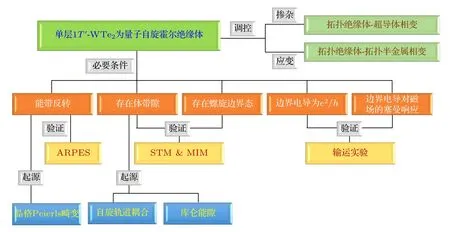
图2 单层1T'-WTe2 中量子自旋霍尔绝缘体的探测及调控Fig.2.Detection and modulation of quantum spin Hall effect in monolayer 1T'-WTe2.

2 单层1T'-WTe2 的晶格和能带结构

TMD 的分子式为MX2,其中M=(Mo,W 等)代表过渡金属原子,X=(S,Se,Te)代表硫族原子.单层TMD 是由X-M-X三个原子层堆垛形成的三明治结构,具有三种典型的结构形态,分别为1H相(空间群P63/mmc)、1T相(空间群P-3m1)、1T'相(空间群P21/m),如图3 所示[15,39].通常来说,单层TMD 的1H相和1T相是热力学稳定的相[40,41].然而,单层MoTe2,WTe2,TaTe2是例外.在这些体系中,单层的1T相是不稳定的,其会自发地存在Peierls 畸变,使中间层的M原子在x方向上会发生位移,形成2×1 超晶格结构,即图3(c)所示的1T'相[40].

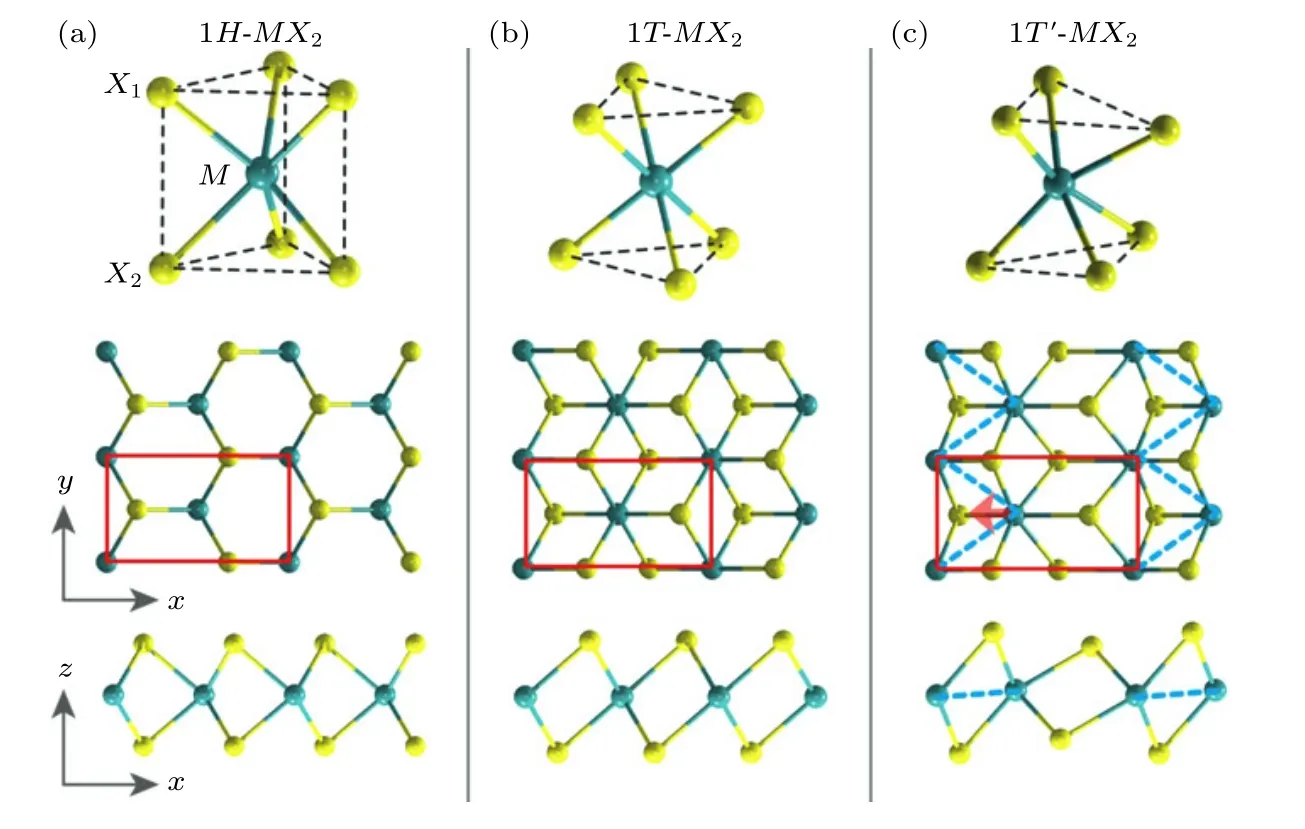
图3 单层过渡金属硫族化合物MX2 的结构示意图[15] (a) 1H-MX2[15];(b) 1T-MX2[15];(c) 1T'-MX2[15]Fig.3.Atomic structures of monolayer TMD MX2[15]:(a) 1H-MX2[15];(b) 1T-MX2[15];(c) 1T'-MX2[15].

单层TMD 由于Peierls 畸变从1T相转变为1T'相的过程中,在二维布里渊区的Γ点处能带会发生反转,如图4 所示[35].当不考虑自旋-轨道耦合时,价带和导带在动量方向Y-Γ-Y出现交叠,形成两个狄拉克点,自旋-轨道耦合进一步将狄拉克点处的简并度解除,形成体能隙.由体边对应关系可知,单层1T'-TMD 的边缘处一定存在非平庸的拓扑边界态[4,42],这意味着单层1T'-TMD 是量子自旋霍尔绝缘体.

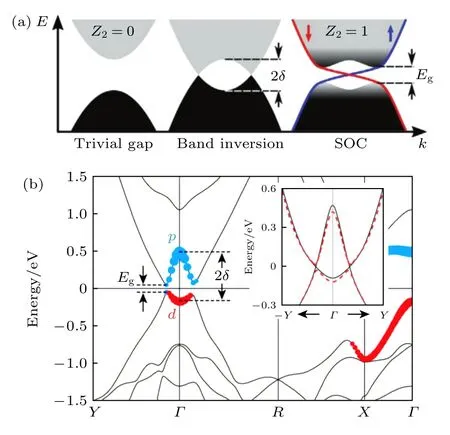
图4 单层1T'-TMD 的能带结构 (a) 能带从拓扑平庸相转变为拓扑非平庸相的示意图.能带的反转导致其从拓扑平庸相转变为拓扑非平庸相,自旋-轨道耦合效应可以进一步使轨道交叠处的简并度解除[35].(b)单层1T'-TMD 的能带结构[15]Fig.4.Band structures of monolayer 1T'-TMD:(a) Schematic of band evolution from a topologically trivial phase to a nontrivial phase.Band inversion causes the band changing from topologically trivial to topologically nontrivial[35];(b) band structure of monolayer 1T'-TMD[15].

下面的介绍将聚焦于具体的材料体系中,即单层WTe2体系.通过第一性原理计算可知,在单层1T-WTe2中,W 原子的 5dxz和 5dz2轨道位于费米面的两侧[27].由于1T'相是1T相发生Peierls 畸变的结果,1T'-WTe2中存在明显的晶格对称性破缺,致使 5dxz和 5dz2轨道向能量相反的方向移动并出现交叠,即发生能带的反转.当引入自旋-轨道耦合时,能带的杂化使 5dxz和 5dz2轨道交叠处狄拉克点的简并度解除,并进一步在其边缘处形成受时间反演对称性保护的螺旋边界态[27,43].此时,体系的Z2拓扑不变量从0 变为1,即能带从拓扑平庸相转变为拓扑非平庸相.因此,单层1T'-WTe2有望成为面向未来应用的一类新型的二维量子自旋霍尔绝缘体.

3 单层1T'-WTe2 的制备与表征

3.1 利用MBE 技术生长单层1T′-WTe2

获得大面积高质量且处于悬浮状态的单层1T'-WTe2是研究其量子自旋霍尔效应的关键.目前,一种比较成熟的方法是利用MBE 技术生长单层1T'-WTe2材料[27,30,38],如图5(a)所示.实验上,通常选择石墨烯作为衬底,一是因为石墨烯具有原子级平整的晶格结构,且性质较为稳定,有助于1T'-WTe2的外延生长;二是因为石墨烯与1T'-WTe2之间是范德瓦耳斯相互作用[30],且石墨烯表面不存在悬挂键,可以有效地避免衬底对边界态的干扰.由于W 原子和Te 原子在相同温度下的蒸气压存在显著的差异,实验上一般控制W 原子和Te原子的束流比约为1∶20,衬底温度控制在200—250 ℃范围内,确保得到高质量的单层1T'-WTe2样品.

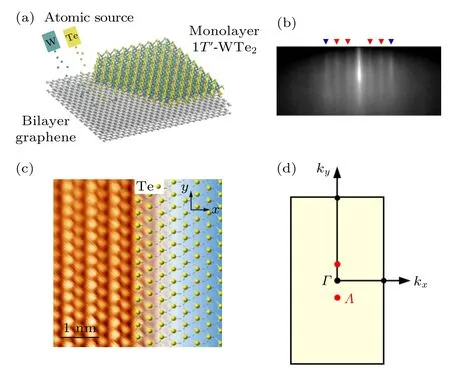
图5 单层1T'-WTe2 的制备与表征 (a)利用MBE 技术生长单层1T'-WTe2 的示意图[30];(b)在石墨烯表面生长单层1T'-WTe2 后的RHEED 图[30],其中蓝色箭头表示来自BLG/SiC(0001)基底的条纹,而红色箭头表示来自单层1T'-WTe2 的3 个等能畴 方向 的条 纹[30];(c) 单 层1T'-WTe2的原子分辨STM 图[54];(d) 单层1T'-WTe2 的布里渊区图[54]Fig.5.Preparation and characterization of the monolayer 1T'-WTe2:(a) Schematic of sample preparation of monolayer 1T'-WTe2 via an MBE method[30].(b) RHEED pattern of monolayer 1T'-WTe2[30].The blue arrow marks the streaks from the BLG/SiC(0001) substrate,while the red arrows represent the ones from WTe2 domains of three equivalent orientations[30].(c) Atomic-resolution STM image of monolayer 1T'-WTe2[54]. (d) Brillouin zone of monolayer 1T'-WTe2[54].

3.2 利用机械剥离技术获得单层1T′-WTe2

机械剥离技术是获得单层1T'-WTe2的重要方法.实验上,首先利用化学气相传输(chemical vapor transport,CVT)等方法实现对高质量单晶1T'-WTe2的制备[44−46];然后在充满氮气的手套箱中,利用胶带从单晶1T'-WTe2中剥离出少层1T'-WTe2样品并转移至285 nm 厚的SiO2衬底上;通过光学显微镜成像,实现对单层1T'-WTe2的辨认;基于干法转移技术,利用热释放胶带将单层1T'-WTe2转移至目标衬底上,进而实现对其晶格结构和电学性质的表征[47−50].此外,脉冲激光沉积技术(pulsed laser deposition,PLD)也是生长高质量拓扑量子薄膜的重要手段,有望实现对高质量单晶1T'-WTe2的可控制备[51−53]

3.3 对单层1T′-WTe2 的结构表征

利用反射式高能电子衍射(reflection highenergy electron diffraction,RHEED)可以对单层1T'-WTe2样品的生长过程进行原位表征.图5(b)为在石墨烯表面生长单层1T'-WTe2后的RHEED图[30].通过石墨烯的晶格常数2.47 Å校准,可得单层1T'-WTe2长轴(a轴)的晶格常数为6.3 Å ±0.2 Å[27].图5(c)给出了单层1T'-WTe2的原子分辨STM 图,图中的亮点由最上层的Te 原子贡献.由于单层1T'-WTe2相对于1T-WTe2存在自发的晶格畸变,中间层W 原子在长轴方向上表现出两倍的周期结构,并在短轴方向上形成一维的锯齿型原子链.W 原子的晶格畸变进一步导致最上层Te原子不再处于同一平面内,因此会在STM 图中表现出明显的高度差,如图5(c)所示[54].图5(d)为单层1T'-WTe2的第一布里渊区.

4 单层1T'-WTe2 的量子自旋霍尔效应

4.1 利用ARPES 探测单层1T′-WTe2 的体能带结构

ARPES 是测量材料体系能带结构的重要手段.图6 是利用ARPES 探测单层1T'-WTe2沿着布里渊区Γ-X方向上的体能带结构.可以看出,由于自旋-轨道耦合,在能带交叠处会打开正能隙,且该能隙在动量方向上不会关闭[55].为了让ARPES中的导带信息更为明显,实验上,通常向体系中引入K 原子实现电子掺杂[27,38].可以发现,当改变电子填充时,由于自旋-轨道耦合打开的正能隙并没有发生显著变化.该实验结果表明,单层1T'-WTe2中的自旋-轨道耦合会导致体能隙的打开.

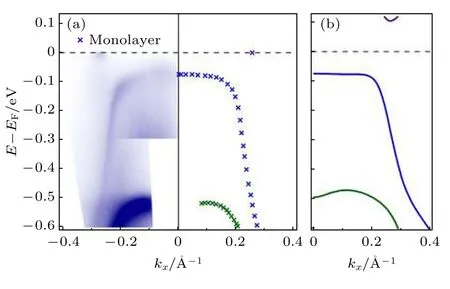
图6 单层1T'-WTe2 的体能带结构 (a) 利用ARPES 探测单层1T'-WTe2 沿着Γ-X 方向的体能带结构[55];(b) 利用第一性原理计算单层1T'-WTe2 的能带结构[55]Fig.6.Band structure of monolayer 1T'-WTe2:(a) Band structure of monolayer 1T'-WTe2 acquired by ARPES along the Γ-X direction[55];(b) calculated band structure of monolayer 1T'-WTe2 along the Γ-X direction by first-principles[55].

4.2 利用STM 探测单层1T′-WTe2 的边界态

量子自旋霍尔绝缘体要求体系具有绝缘的体能隙和导电的一维螺旋边界态.STM 和STS 具有高空间分辨率和能量分辨率,可为一维边界态的存在提供重要的实验证据[22,27,30,38].STM 实验的研究结果表明,无论是在绝对单层的1T'-WTe2体系中[27],还是在1T'-WTe2的单层台阶处[29],都存在着一维边界态.这里将以1T'-WTe2的单层台阶为例,具体介绍利用STM 探测一维边界态的方法.

图7(a)为1T'-WTe2单层台阶处的STM 图,图7(b)为其典型的STS 谱,它可以直接反映不同探测位置的局域态密度.在图7(b)中,黑线为单层1T'-WTe2岛内部的STS 谱,它在费米面附近存在能隙.而在边界处,费米面附近的STS 谱出现态密度峰,这意味着单层1T'-WTe2存在一维的导电边界态[27].图7(c)为STS 谱在跨过1T'-WTe2单层台阶过程中的演化情况.可以发现,费米面附近态密度峰所代表的边界态只存在于1T'-WTe2的单层台阶处,且和样品的尺寸、形状、台阶的整齐程度无关.这些实验现象表明,1T'-WTe2的单层台阶具有拓扑非平庸的边界态.

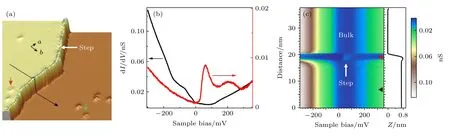
图7 利用STM 探测1T'-WTe2 单层台阶处的一维边界态[29] (a) 1T'-WTe2 单层台阶的STM 图;(b) 1T'-WTe2 内部(黑线)和单层台阶边缘处(红线)的STS 谱;(c)空间分辨的STS 谱,横坐标表示探测点到1T'-WTe2 单层台阶的距离,x=0 nm 为1T'-WTe2 的单层台阶Fig.7.STM detection of edge states in 1T'-WTe2 monolayer step:(a) STM image of 1T'-WTe2 monolayer step[29];(b) typical STS spectra recorded at the step edge (red curve) and at a location at the inner terrace (black curve) of 1T'-WTe2[29];(c) spatial-resolved STS spectra recorded perpendicular to the 1T'-WTe2 monolayer step.The position x=0 nm is at the monolayer step[29].

4.3 利用MIM 探测单层1T′-WTe2 的拓扑边界态

MIM 技术通过测量分析导电针尖与样品之间的复数导纳,可以得到样品的局域电导信号,而电导的空间分布情况正是边界态是否存在的直观体现[32,56−59].其中,MIM 信号的虚部(MIM-Im)反映样品对针尖上微波电场的屏蔽情况,当样品的电阻率降低时,MIM-Im 的信号强度单调增加.因此,利用MIM-Im 可以直观地测量样品的局域电导强度.

2019 年,Shi 等[32]利用电场调控的MIM 实现了对单层1T'-WTe2中拓扑边界态的测量.图8(a)给出了样品的光学显微镜图,单层1T'-WTe2通过机械剥离法转移到SiO2/Si 衬底上,并在上表面覆盖了10 nm 厚的hBN,防止样品被污染或变质.图8(b)—(d)为零磁场下的MIM-Im 图,分别对应图8(a)中3 个标注的区域.可以发现,单层1T'-WTe2内部的MIM-Im 信号强度与SiO2/Si 衬底相差不大,说明其体内是绝缘的.然而,在单层1T'-WTe2的边界处存在明显的亮线,且亮线严格地沿着样品的边缘,强度与边缘的形状无关,说明单层1T'-WTe2的边缘存在一维的导电通道.

利用电场调控的MIM 可以进一步证实该一维导电通道的拓扑行为.理论上,一维拓扑导电通道连接了体能带的导带底和价带顶,因此边界态几乎不受费米面的影响;相反,由于能带弯曲等因素诱导的平庸边界态会格外依赖于费米面的能量.因此,通过测量一维边界态随费米能的变化,可以有效地判断其拓扑性质.图8(e)为零磁场下穿过单层1T'-WTe2边界的MIM-Im 信号随栅极电压的变化情况.可以发现,在费米面从单层1T'-WTe2的导带到体能隙再到价带变化的过程中,当费米面处于体能隙时,边缘处的一维导电通道一直存在.这个现象证实了单层1T'-WTe2具有受拓扑保护的一维导电通道.

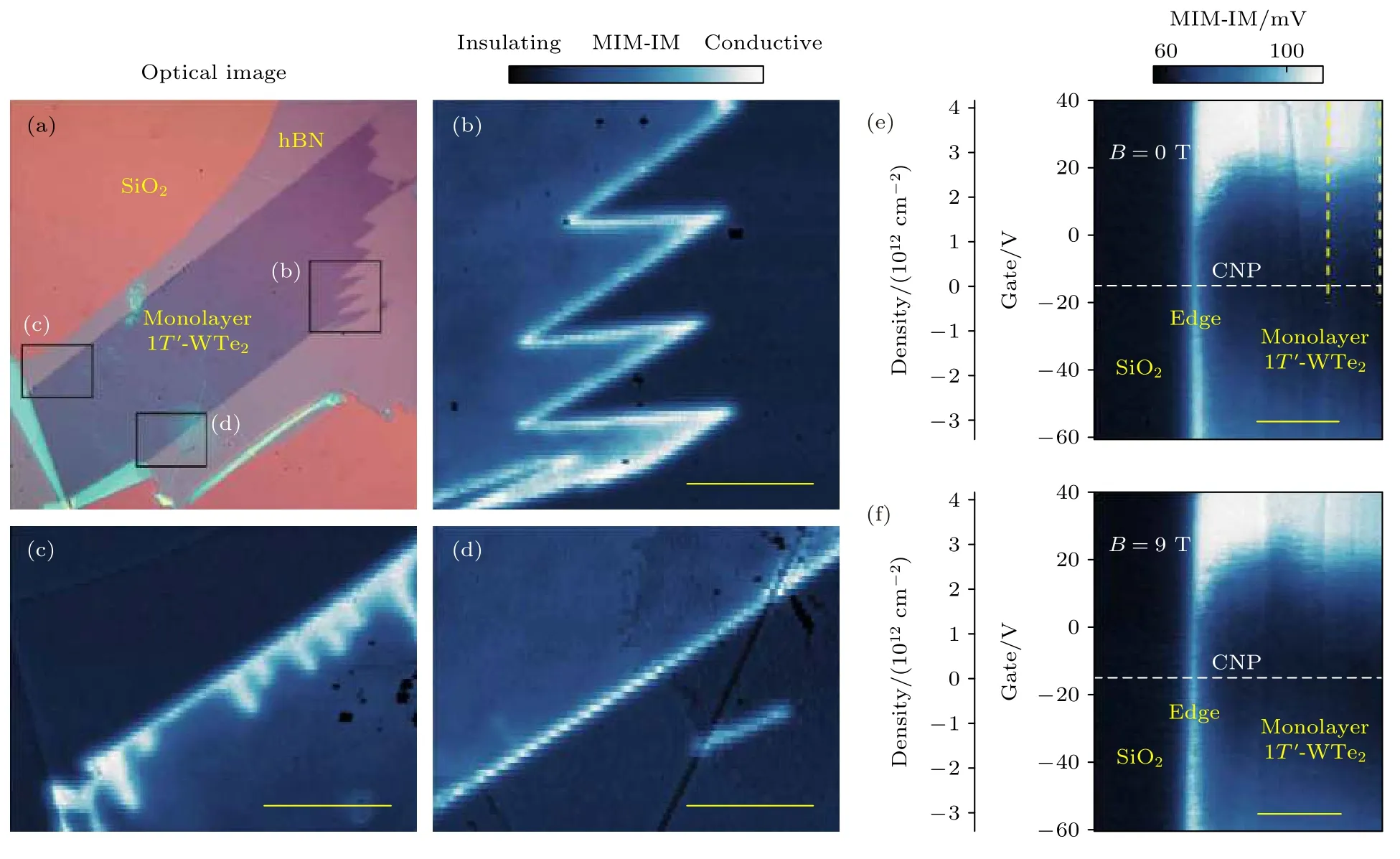
图8 利用MIM 探测单层1T'-WTe2 的边界态[32] (a)样品的光学显微镜图,单层1T'-WTe2 被转 移到SiO2/Si 衬底 上,并覆盖10 nm 厚的hBN;(b)—(d) 图(a)中不同区域对应的零磁场下MIM-Im 图;(e)穿过单层1T'-WTe2 边界的零磁场下MIM-Im 信号随栅极电压的变化情况,其中EGate=–15 V 为电中性点的位置;(f)穿过单层1T'-WTe2 边界的B=9 T 下MIM-Im 信号随栅极电压的变化情况Fig.8.Detection of edge states in monolayer 1T'-WTe2 via an MIM technique:(a) Optical image of monolayer 1T'-WTe2 exfoliated onto SiO2/Si substrate and covered with a 10-nm-thick hBN[32].(b)–(d) MIM-Im images of the regions marked in panel (a) [32].(e) MIM-Im images obtained across the edge of monolayer 1T'-WTe2 as a function of gate voltage EGate under B=0 T[32].The charge neutral point is located at EGate=–15 V[32].(f) MIM-Im images obtained across the edge of monolayer 1T'-WTe2 as a function of gate voltage EGate under B=9 T[32].

利用磁场调控的MIM 可以进一步证实单层1T'-WTe2具有螺旋边界态.在垂直磁场的作用下,螺旋边界态会发生杂化,在靠近体带边时会打开塞曼能隙,同时伴随着电阻率的升高[32].图8(f)为在B=9 T 的垂直磁场下,穿过单层1T'-WTe2边界的MIM-Im 信号随栅极电压的变化情况.可以看到,单层1T'-WTe2体内的MIM 信号几乎不随磁场发生变化,而边缘处的MIM-Im 信号有微弱的衰减,这正是螺旋边界态的典型特征.

4.4 利用电荷输运实验探测单层1T′-WTe2的量子自旋霍尔效应

利用电荷输运实验测量单层1T'-WTe2的边界电导可以为证实体系中存在量子自旋霍尔效应提供最直接和重要的证据[15,28−31].通常来说,量子自旋霍尔效应的电荷输运测量结果需要同时满足以下两点[1,7,8,10,12]:1) 每个边界都具有量子电导平台e2/h(e为电子电荷,h为普朗克常数);2) 外加磁场通过破坏体系的时间反演对称性使其螺旋边界态消失,进而有效地抑制电导.

2018 年,美国麻省理工学院的Jarillo-Herrero团队[31]成功地在单层1T'-WTe2体系中探测到了量子自旋霍尔效应.他们利用背栅电压Vc调控长度为Lc的待测单层条状1T'-WTe2样品,样品的其他部分通过顶栅电压Vtg实现重掺杂,以便有效地避免接触电阻的影响(图9(a)).图9(b)为在不同长度的单层1T'-WTe2中,电阻差值ΔR随局域背栅电压Vc的变化曲线,其中ΔR=R(Vc)–R(Vc=–1 V),R(Vc=–1 V)为重掺杂时的电阻.由图9(b)可知,随着Vc的降低,即单层1T'-WTe2从体金属态(掺杂)到体绝缘态(未掺杂)的转变过程中,ΔR逐渐趋于饱和,阻值接近h/(2e2),且在Lc<100 nm 的短通道器件中都存在,如图9(b)和图9(c)所示,说明其为单层1T'-WTe2本征的属性.考虑到Vc较小时为体绝缘态,则饱和电阻完全由单层1T'-WTe2的边界贡献,而样品存在两个边界,则每个边界的电导约为e2/h,这与量子自旋霍尔效应的螺旋边界态一致.

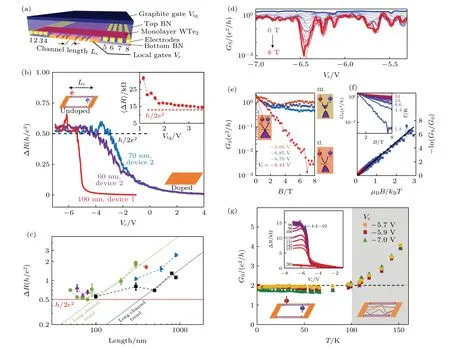
图9 利用电荷输运测量单层1T'-WTe2 的量子自旋霍尔效应[31] (a)基于单层1T'-WTe2 器件的示意图.器件由单层1T'-WTe2、用于封装的hBN、石墨顶栅、8 个接触电极,以及长度不一的一系列局域背栅组成.(b)电阻差值ΔR 随局域栅极电压Vc 的变化曲线,其中局域背栅的宽度分别为100,70 和60 nm.(c)长度依赖的电阻.在短通道极限下,ΔRs 接近于电阻最小值h/(2e2),这意味着每个边界的电导为e2/h,满足量子自旋霍尔效应.(d)在垂直磁场下,边界电导GS 随Vc 的变化曲线,背栅宽度为100 nm.(e)在特定的Vc 下,GS 随磁场的变化曲线.电导是否出现饱和取决于费米面的位置.(f)–ln(GS/G0)随µBB/(kBT)的变化.黑线为线性拟合的结果.插图:对于电导不饱和的情况,在不同温度下测量GS 随磁场的变化;(g)边界电导随温度的变化情况.插图:不同温度下ΔR 随Vc 的变化曲线[31]Fig.9.Observation of quantum spin Hall effect up to 100 K in monolayer 1T'-WTe2 via transport measurements[31]:(a) Schematic of monolayer 1T'-WTe2 encapsulated with hBN.Graphite is applied for the top gate,eight contact electrodes are applied to minimize the effect of contact resistance,and a series of in-channel local bottom gates are applied to study the length-dependent feature.(b) ΔR versus Vc for the gate with the width of 60,70,and 100 nm.(c) Length dependence of ΔRs.In the short-channel limit,the ΔRs values approach a minimum of h/(2e2),in agreement with quantum spin Hall effect.(d) GS versus Vc under perpendicular magnetic fields for a 100-nm-width gate.(e) GS versus B at specific Vc.The saturation or not of GS depends on the Fermi energy.(f)–ln(GS/G0) versus µBB/(kBT).The black line is a linear fit.Inset:Temperature dependence of GS versus B for the non-saturating curves.(g) Temperature dependence of the edge conductance.Inset:gate dependence of ΔR at various temperatures.

电阻/电导对外加磁场的响应是证明单层1T'-WTe2具有量子自旋霍尔效应的另一重要手段[31].图9(d)为磁场下电导GS=1/ΔRs(ΔRs为Lc<100 nm 的短通道电阻差值)随局域背栅电压Vc的变化曲线.从图9(d)可以看出,随着磁场的增加,单层1T'-WTe2的GS发生明显的衰减.GS随磁场的变化规律可以分为以下两种情况:当Vc接近–6.44 V时,GS随着磁场的增加呈指数下降,且即使磁场高达8 T 也没有出现饱和的迹象;而对于其他的Vc值,GS在高磁场下达到饱和,如图9(e)所示.

这个现象与量子自旋霍尔效应具有显著的关联.量子自旋霍尔绝缘效应存在一维螺旋边界态,其中自旋向上和自旋向下电子对应的能带在Kramers简并点相交,如图9(e)中插图I 所示.当费米面位于体带隙时,外加磁场通过塞曼效应有效地破坏了Kramers 点的简并度,使其打开能隙,如图9(e)中插图Ⅱ所示,此时的电导不存在饱和值.进一步测量GS随温度的变化,可以发现–ln(GS/G0)与µBB/(kBT)存在线性关系(G0为零场下的电导,µB为玻尔磁子,kB为玻尔兹曼常数,T为温度),通过拟合斜率可得体系的有效g因子为4.8,满足塞曼效应的规律,如图9(f)所示.该结果说明磁场可以通过塞曼效应打开单层1T'-WTe2边界处的能隙,这是螺旋边界态的直观体现.此外,从图9(g)可以看出,在零磁场条件下当温度升至100 K 时,该量子化的电导仍然存在[31].因此,该实验证实了单层1T'-WTe2表现为高温量子自旋霍尔效应.

5 单层1T'-WTe2 中体绝缘态的物理起源

第一性原理计算结果表明,本征单层1T'-WTe2的体能带为半金属[15],而实验上,体能带通常表现为绝缘体的性质[27,28].目前,基于单层1T'-WTe2中体绝缘态的物理起源问题有两种主流的观点:一种是单层1T'-WTe2由于自旋-轨道耦合打开的体能隙为正能隙;另一种是单层1T'-WTe2由于自旋-轨道耦合打开的体能隙为负能隙,而费米面附近会出现电子-电子相互作用产生的库仑能隙.

第一种观点主要是基于ARPES 实验结果和大部分的输运实验结果.2017 年Tang 等[27]利用ARPES 测量单层1T'-WTe2的体能带结构,发现其由于自旋轨-道耦合而打开的能隙始终为正能隙,且能隙的正负与电子的填充无关.同时,基于电荷输运实验在单层1T'-WTe2中测得量子化边缘态也正是其体能带结构存在正能隙的直观体现[31].理论上,通过考虑单层1T'-WTe2中的电子-电子相互作用,也同样可计算出其能带结构中的正能隙[27].

另一种观点主要是基于STM 实验结果.2018年,Li 团队[54]利用STS 图和准粒子干涉(quasiparticle interference technique,QPI)技术实现对单层1T'-WTe2能带结构的测量.图10(a)为单层1T'-WTe2中体内的低能STS 谱.可以发现,在费米面附近存在能隙,且在接近–60 meV 的能量处存在态密度的极小值.图10(b)为不同能量下的STS图经过傅里叶变换后的结果,其波矢q=kf–ki为电子的布洛赫波从初始态ki散射到末态kf的动量变化.对比图10(c)中给出的单层1T'-WTe2的能带结构可知,第一布里渊区中心用粉色和红色标注的椭圆分别为导带的带内散射q1和价带的带内散射q4,它们在高能量时独立出现,而在低能量时由于发生交叠而同时出现.在第一布里渊区沿着Y-Γ-Y方向对称的两套椭圆分别为导带的带间散射q2(绿色)和价带-导带的带间散射q3(橘黄色)[54].图10(d)为通过QPI 技术测得的沿着Y-Γ-Y方向的能量-动量色散关系,其中,q2—q4已在图中用黑线标注[54].从图中可知,q3在一定的能量范围内出现,这意味着由于自旋-轨道耦合引起的狄拉克点简并度的解除并不能完全打开能隙(负能隙),与基于单电子模型的计算结果一致.而费米面附近单层1T'-WTe2的绝缘特性来源于多体相互作用.通过电子掺杂,发现单层1T'-WTe2的体带隙一直位于费米面,如图10(e)所示,这说明该带隙来源于电子间的库仑相互作用.该实验结果表明,单层1T'-WTe2由于自旋-轨道耦合,在能带交叠处会打开负能隙,而在费米面附近,由于电子-电子相互作用的存在,会打开库仑能隙.考虑到单层1T'-WTe2的晶格结构对其能带结构有显著的影响,而衬底可以使单层1T'-WTe2的晶格发生微小的拉伸和压缩,因此,样品的制备方式的不同(包括MBE 和机械剥离技术)和细微晶格结构的差异可能是影响单层1T'-WTe2能带结构的重要原因.

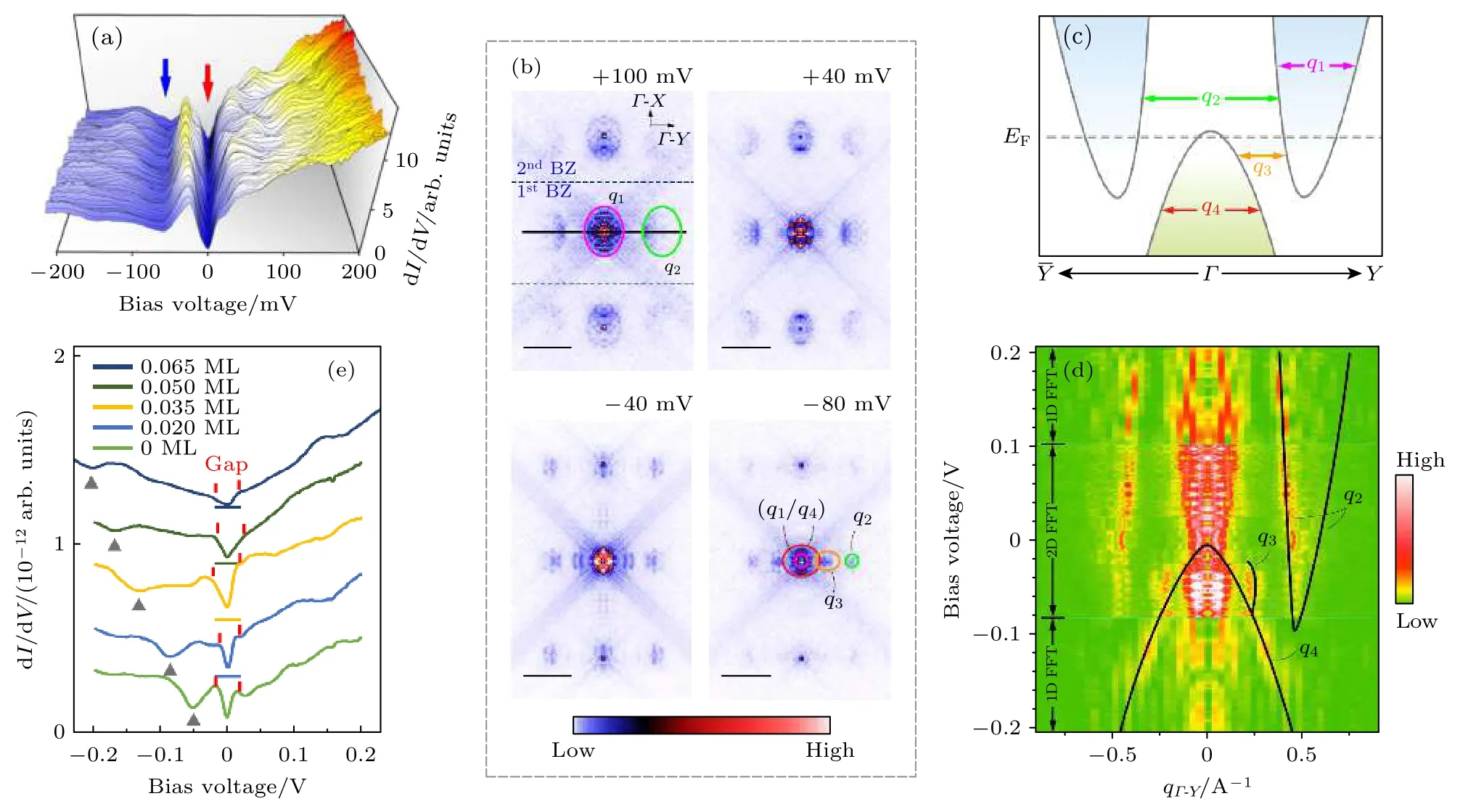
图10 利用STS 探测单层1T'-WTe2 中体绝缘态的物理起源[54] (a)在单层1T'-WTe2 体内不同位置的低能STS 谱,红色箭头表示库仑能隙,蓝色箭头表示局域态密度降低的能量位置;(b)不同能量STS 图的傅里叶变换结果;(c)沿着动量Y-Γ-Y 方向的能带结构示意图,其中q1 为导带的带内散射,q2 为两个导带间的带间散射,q3 为导带和价带间的带间散射,q4 为价带的带内散射;(d)通过不同能量STS 图的傅里叶变换得到的单层1T'-WTe2 能量-动量色散关系,其中黑线为q1,q2,q3 带色散;(e)不同浓度K 掺杂单层1T'-WTe2 得到的STS 谱,费米面处存在库仑能隙Fig.10.STS evidence of the physical origin of the bulk insulator in monolayer 1T'-WTe2[54]:(a) Spatially resolved low-energy STS spectra recorded in the bulk of monolayer 1T'-WTe2.The Coulomb gap and the minimum of local density of states are marked by the red and blue arrows,respectively.(b) The fast Fourier transform (FFT) image of the STS maps at different energies.(c) Band structures of monolayer 1T'-WTe2 along the direction of Y-Γ-Y in the reciprocal space.The corresponding scattering channels of are the intra-band scattering of the conduction band (q1),the inter-conduction band scattering (q2),the inter-band scattering between the valence and conduction bands (q3),and the intra-band scattering of the valence band (q4).(d) Energy-momentum dispersion along the Y-Γ-Y direction.The black lines schematically illustrate the band dispersion of q2,q3,and q4.(e) STS spectra taken on the 1T'-WTe2 surface with different potassium coverage.The Coulomb gap is located at the Fermi energy.

6 调控单层1T'-WTe2 中的拓扑绝缘态

6.1 利用电场在单层1T′-WTe2 中实现二维拓扑绝缘体-超导相变

2018 年,Sajadi 等[36]与Fatemi 等[37]通过轻掺杂单层1T'-WTe2体系,分别实现了将单层1T'-WTe2从二维拓扑绝缘态转变为超导态.通过将单层1T'-WTe2的上下表面用介电层hBN 封装并引入电极(图11(a)),可以测得不同温度下,Rxx随电子掺杂浓度ne的变化关系,如图11(b)所示.其中,Rxx=dV/dI为四探针法测得的电阻,ne=(ctVt+cbVb)/e为电子掺杂浓度(ct和cb分别为顶栅和背栅的电容,Vt和Vb分别为顶栅和背栅的电压).可以发现,在当单层1T'-WTe2未被掺杂时,体系表现为二维拓扑绝缘体的特征;当电子掺杂浓度ne超过临界值ncrit≈5×1012cm–2时,电阻急剧下降,且当温度低于20 mK 时电阻可达至0.3 Ω,这意味着体系中出现了超导态.图11(c)给出了该调控过程的相图.

下面将进一步介绍轻掺杂单层1T'-WTe2体系中的超导特性.图11(d)—(f)分别给出了在超导的单层1T'-WTe2中,Rxx随温度T、垂直磁场B⊥、平行磁场B∥的变化情况.这里定义T1/2为Rxx降低至1 K 时Rxx的一半时的温度,B1/2为Rxx降低至其一半时的磁场.从图11(d)可知,对于所有的ne,Rxx随着温度的升高而下降的过程都是缓慢的,这是由于二维超导体正常态的电导不会超过e2/h.图11(c)中的红色圆点为以T1/2为标准给出的超导边界.同时,单层1T'-WTe2体系中的超导态也可以被垂直磁场B⊥和平行磁场B∥有效地抑制[36].由图11(e)可得,(T0)≈25 mT,且超导相干长度约为100 nm;由图11(f)可得,≈3T.

此外,单层1T'-WTe2中二维拓扑绝缘态与超导态在相图上的近邻关系暗示着螺旋边界态与超导态之间可能存在某种关联[23,36,37].图11(g)为单层1T'-WTe2在不同温度T和垂直磁场B⊥下,电导随ne的变化曲线.在T=200 mK 且B⊥=0 T 的条件下,当ne较低时,单层1T'-WTe2体内是绝缘的而边界是导电的;当ne>2×1012cm–2时,电导随着体内逐渐导电而增加;一旦ne>ncrit,超导态的出现导致电导快速增加.而当温度升至T=1 K 时,超导态不再存在,因此当ne>ncrit时电导相对于T=200 mK 时降低,当ne较低时边界电导升高并接近理论值e2/h=39 µS.同样地,B⊥=50 mT 的垂直磁场也可以有效地破坏超导态,导致当ne>ncrit时电导相对于B⊥=0 T 时降低,这是由于磁场可以通过破坏二维拓扑绝缘体中的时间反演对称性来有效地抑制边界电导.那么,如果此时将磁场降为零,可能会出现超导态和螺旋边界态共存的现象,这也暗示着体系中存在非常规超导配对和非平凡的拓扑序,值得进一步探索.

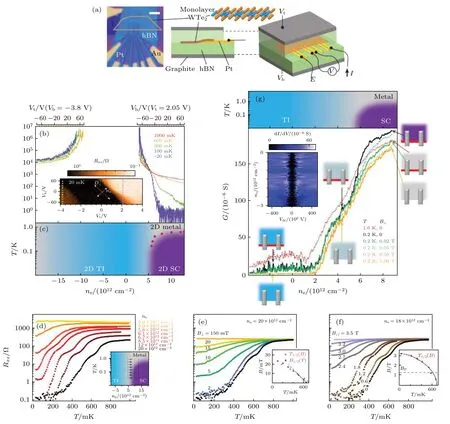
图11 在单层1T'-WTe2 中实现二维拓扑绝缘体-超导相变[36] (a) 基于单层1T'-WTe2 器件的光学显微镜图及模型图,其中单层1T'-WTe2 用hBN 介电层封装,并通过石墨引入电极;(b)在不同温度下,Rxx 随电子掺杂浓度ne 的变化关系;(c)在单层1T'-WTe2 中发生二维拓扑绝缘体-超导转变的相图;(d)在不同ne 下,Rxx 随温度的变化曲线;(e)在高ne 时,Rxx 随垂直磁场强度的变化关系,其中插图为T1/2 随温度的变化以及B1/2 随垂直磁场的变化;(f)在高ne 时,Rxx 随平行磁场强度的变化关系,其中插图为T1/2 随平行磁场的变化,虚线为g 因子为2 时的泡利极限值BP;(g)在不同温度和垂直磁场下,电导随掺杂浓度的变化曲线,其中示意图为不同位置单层1T'-WTe2 体和边界的到点情况,其中体态的颜色与相图一致,边界态用红色表示Fig.11.Realization of phase transition between two-dimensional topological insulating states and superconductivity in monolayer 1T'-WTe2 [36]:(a) Optical image and schematic device structure of monolayer 1T'-WTe2 with encapsulated hBN dielectric layers and two graphite gates.(b) Rxx as a function of electrostatic doping ne under different temperatures.(c) experimental phase diagram of phase transition between two-dimensional topological insulating states and superconductivity in monolayer 1T'-WTe2.(d) Rxx as a function of temperature under different ne.(e) Rxx as a function of perpendicular magnetic field at the highest ne value.Inset:T1/2 as a function of temperature,as well as B1/2 as a function of perpendicular magnetic field.(f) Rxx as a function of parallel magnetic field at the highest ne value.Inset:T1/2 as a function of parallel magnetic field.The Pauli limit BP,assuming g factor of 2,is indicated by the dashed line.(g) Conductance as a function of ne under different temperatures and perpendicular magnetic field.Schematics indicate the state of edge and bulk conduction of monolayer 1T'-WTe2 at different points.The bulk is colored to match the phase diagram,and red indicates a conducting edge state.

6.2 利用应力在单层1T′-WTe2 中实现半金属-绝缘体相变

有效调控量子自旋霍尔绝缘体中的体带隙对自旋电子学器件的发展具有重要的意义[24].2020年,Zhao 等[38]利用STM 首次证实应力可以使单层1T'-WTe2从二维拓扑半金属态转变为拓扑绝缘态.图12(a)—(c)给出了在应力的作用下,单层1T'-WTe2的原子分辨STM 图及其STS 谱.从图12(a)—(c)可以看到,当晶格常数不同时,STS谱存在显著的差异,且在某些特定的应力下,费米面附近表现出明显的带隙.图12(d)和图12(e)为费米附近的能隙随单层1T'-WTe2晶格常数的变化关系.从图12(d)和图12(e)可以看出,单层1T'-WTe2长轴(a轴)的压缩或短轴(b轴)的拉伸都可以导致体能隙的增加,即实现单层1T'-WTe2从半金属到绝缘体的转变[35].

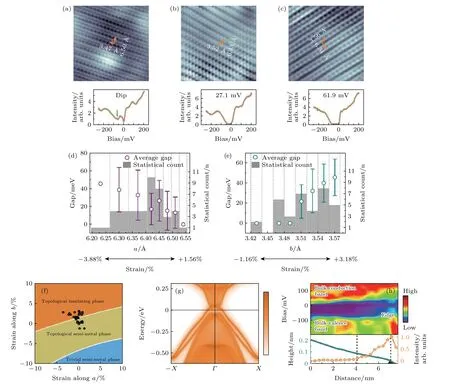
图12 利用应力在单层1T'-WTe2 中实现绝缘体-半金属相变[38] (a)—(c)在应力作用下,单层1T'-WTe2 的原子分辨STM 图及其STS 谱;(d),(e)单层1T'-WTe2 的体带隙随其晶格常数a 和b 的变化;(f)单层1T'-WTe2 随晶格常数a 和b 变化的相图,其中实验上测得的结果用黑色圆圈标注;(g)理论计算单层1T'-WTe2 的A 边界能带结构,计算的晶格常数a=6.33 Å,b=3.54 Å;(h)垂直于A 边界的空间分辨STS 谱,可以看到明显的一维边界态Fig.12.Strain tunable phase transition between topological insulator and semimetal insulator in monolayer 1T'-WTe2[38]:(a)−(c) Atomically resolved STM images and corresponding STS spectra in monolayer 1T'-WTe2 under strain.(d),(e) Energy gap as a function of strains along the a or b directions in monolayer 1T'-WTe2.(f) Phase diagram of monolayer 1T'-WTe2 as a function of lattice constants a and b.Strain conditions acquired from the experimental data are marked by black circles.(g) Calculated edge states along the A edge with the lattice constants a=6.33 Å,b=3.54 Å.(h) Spatially resolved STS spectra recorded across the A edge.One-dimensional edge states can be clearly identified.

这个现象可以用轨道理论来解释[38]:单层1T'-WTe2的导带和价带分别由W 原子的dxz和Te 原子的py轨道主导.在a轴方向上,dxz轨道呈现类似于ddπ*的反键态,而py轨道呈现类似于ppπ 成键态.当对单层1T'-WTe2施加沿着a轴(b轴)方向的拉(压)应力时,ddπ*和ppπ 都变弱,使得导带的能量降低而价带的能量升高,进而增强了它们之间的耦合,导致金属性变强.然而,当对体系施加沿着a轴(b轴)方向的压(拉)应力时,ddπ*和ppπ都增强,使得导带的能量升高而价带的能量降低,导致它们的能量交叠变少,直至消失,实现半金属-绝缘体的相变.值得注意的是,利用MBE 生长的单层1T'-WTe2的晶格常数通常处于拓扑半金属和拓扑绝缘体的交界处,且拓扑边界态在应力的作用下是稳定存在的,如图12(f)—(h)所示[38],这为单层1T'-WTe2中拓扑态的调控带来了便利.

7 总结与展望

以单层1T'-WTe2为代表的二维TMD 材料体系具有丰富的物理性质,为研究新奇量子物态提供了理想的平台.本文主要综述了单层1T'-WTe2这一新型二维量子自旋霍尔绝缘体在实验上的最新进展.量子自旋霍尔绝缘体的必要条件,包括能带的反转、体能隙的存在、螺旋边界态的存在、边界为e2/h量子霍尔电导、以及该电导对磁场的塞曼响应等,近年来已被ARPES,STM,STS,MIM和电荷输运等实验手段相继证实.更进一步,通过电子掺杂和应力等调控手段,成功地在体系中引入更多新奇的量子物态,包括拓扑绝缘体、拓扑半金属、超导等.

然而,基于单层1T'-WTe2的基础研究仍面临着很大的挑战,其中最重要的问题是高质量、大面积单层1T'-WTe2样品的制备工艺尚未成熟.目前,量子自旋霍尔效应都是在机械剥离的单层1T'-WTe2样品中实现的,然而以这种方法得到的薄膜尺寸有限且产量较低,这大大地限制了其应用.利用MBE 和化学气相沉积技术虽然可以实现大面积单层1T'-WTe2薄膜的可控制备,但是薄膜的质量依赖于衬底的选择,且不可避免地会引入缺陷和杂质等,极大地影响了材料本征的性质.同时,单层1T'-WTe2的转移技术尚未成熟,在转移的过程中不可避免地会对样品造成破坏,限制了基于单层1T'-WTe2器件的制备与性能测量.因此,可控制备高质量、大面积单层1T'-WTe2样品和完善基于二维材料的干法转移技术是亟待解决的问题.此外,基于单层1T'-WTe2的物性研究值得更加深入的探索,例如,如何利用更简单、更便捷、更可靠的技术实现对其中新奇量子物态的调控;二维量子自旋霍尔态与超导态等其他物态之间量子序的关联;是否存在更多新奇的量子物态;以及相变的微观机理等,这在低功耗、小尺寸、高可靠性的自旋电子学器件领域具有广泛的应用前景.更进一步,如果能在单层1T'相TMD 材料中通过近邻效应、离子掺杂等手段引入磁性、超导等物态,这将对马约拉纳费米子研究、拓扑量子计算等领域的发展具有重大的意义.