低介电常数MgxZn1.8−xSiO3.8微波陶瓷的结构与性能

段佳露，周港怀，刘绍军

低介电常数MgZn1.8−xSiO3.8微波陶瓷的结构与性能

段佳露，周港怀，刘绍军

(中南大学 粉末冶金国家重点实验室，长沙 410083)

采用传统固相合成法制备硅锌矿结构 MgZn1.8−xSiO3.8(=0～0.4)陶瓷，结合X射线衍射谱、拉曼光谱、扫描电镜和网络矢量分析仪等，研究Mg掺杂对低介电常数Zn1.8SiO3.8基微波陶瓷的晶体结构、微观形貌与微波性能的影响。结果表明：在1 300 ℃烧结温度下，随Mg掺杂量增加，MgZn1.8−xSiO3.8微波陶瓷的理论极化率减小，相对介电常数相应减小；氧四面体的平均扭转度先减小后增大，导致谐振频率温度系数先减小后增大；由Zn(1)/Mg(1)O4、Zn(2)/Mg(2)O4、和SiO4四面体组成的六元环对称性增强；同时Zn(Mg)－O键长减小，键能增大，导致品质因子×增大。Mg0.4Zn1.4SiO3.8陶瓷性能优异，相对介电常数r约为6.2，×约为112 100 GHz，谐振频率温度系数f约为−19.2×10−6℃。

低介电常数；微波陶瓷；掺杂；晶体结构；微波性能

1 实验

1.1 MgxZn1.8−xSiO3.8陶瓷的制备

以MgO、ZnO、SiO2为原料(均为Aladdin公司生产，纯度≥99.9%)，采用传统固相合成法(在1 000～ 1 500 ℃，固体界面间经过接触、反应、成核和晶体生长，生成复合氧化物)制备MgZn1.8−xSiO3.8陶瓷。首先根据MgZn1.8−xSiO3.8(=0、0.1、0.2、0.3、0.4)化学式称量高纯MgO、ZnO、SiO2粉末，以无水乙醇为介质，在装入ZrO2磨球的尼龙球磨罐中球磨20 h 。将球磨后的混合物在75 ℃干燥箱中干燥、过60目筛，然后利用马弗炉(KSL-1700X-A2)在1 200 ℃预烧3 h 。在预烧粉末中添加石蜡和硬脂酸作为黏结剂与脱模剂（添加量分别为粉末质量的5%和3%)，再次球磨10 h后干燥、造粒，用手动压样机(型号WM01269SC)在4 MPa压力下压制成直径为10 mm、高度4～5 mm 的圆柱形生坯。将生坯在400 ℃保温90 min脱脂，随后用马弗炉(型号KSL-1700X-A2)在1 200～1 350 ℃烧结3 h，得到MgZn1.8−xSiO3.8(=0～0.4)微波陶瓷。

1.2 测试与表征

采用阿基米德排水法测定MgZn1.8-xSiO3.8微波陶瓷的密度，用X射线衍射仪(Ultima IV，Rigaku，Japan)进行物相成分和晶体结构分析，Cu-Kα射线，扫描范围2为 5°～120°。利用拉曼光谱(Labram Aramis, Horiba Jobin)分析陶瓷的化学键振动，扫描波数范围为40～1 000 cm−1。用扫描电镜(Quanta FEG-250, USA)观察陶瓷材料的微观结构，用微波矢量网络分析仪(N5230A，Santa Clara，Agilent，USAN5230A, USA)测定陶瓷的微波性能。

2 结果与讨论

2.1 密度

图1所示为不同温度烧结的MgZn1.8−xSiO3.8(=0、0.1、0.2、0.3、0.4，下同) 陶瓷的密度。由图可见，烧结温度对MgZn1.8−xSiO3.8陶瓷密度有显著影响，随烧结温度升高，陶瓷密度先升高后降低。最佳烧结温度为1 300 ℃，陶瓷密度达到最大值，因此在研究Mg掺杂量对陶瓷组织与性能影响时，选择烧结温度为1 300 ℃。从图1还看出，在相同烧结温度下，随Mg离子掺杂量增加，陶瓷密度逐渐降低，这与陶瓷理论密度降低有关。MgZn1.8−xSiO3.8陶瓷的理论密度可用下式计算[15]：

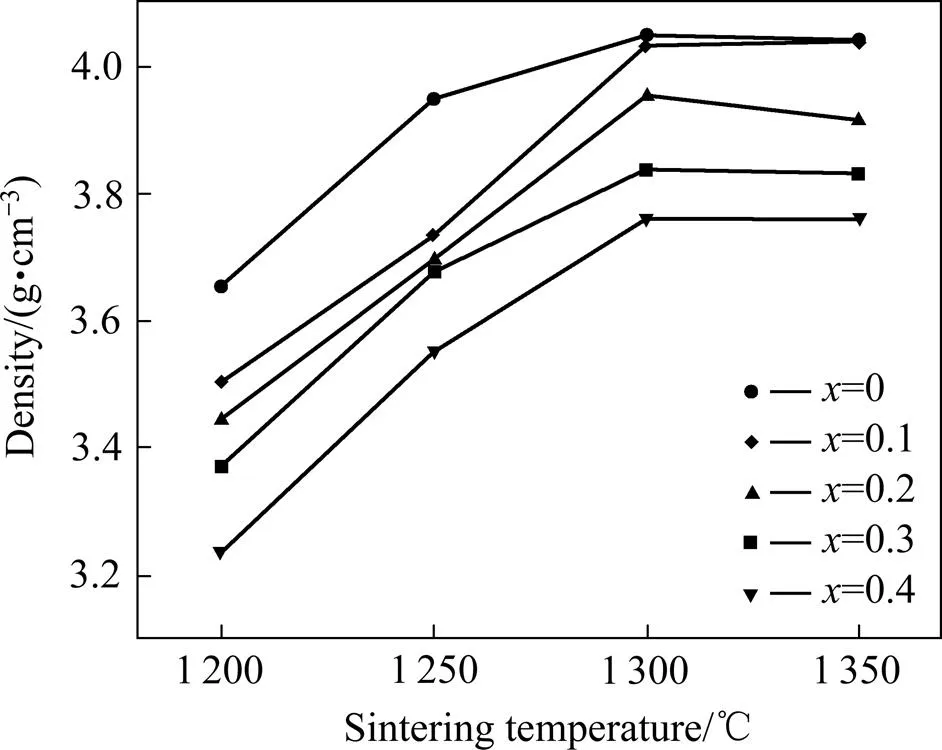
图1 MgxZn1.8-xSiO3.8 (x = 0, 0.1, 0.2, 0.3, 0.4)陶瓷密度随烧结温度的变化

式中：为密度，为单个晶胞中的分子数，为晶胞体积，0为阿伏伽德罗常数，6.022×1023mol−1；r为MgZn1.8−xSiO3.8的相对分子质量。从式(1)可知，由于Mg的相对原子质量小于Zn的相对原子质量，随Mg掺杂量增加，M减小，故陶瓷的密度减小。

2.2 晶体结构

图2所示为1 300℃烧结的MgZn1.8−xSiO3.8陶瓷XRD谱。在传统固相合成过程中，由于SiO2的化学性质不活泼，与ZnO反应不充分，陶瓷中出现第二相ZnO和SiO2，将显著增加陶瓷材料的介电损耗。目前主要采用掺杂[16]、减小粒径[17]等措施来提高粉末的反应活性，进而减少陶瓷中的第二相。而对于Zn2SiO4体系而言，常通过调控ZnO与SiO2的比例来控制第二相的产生[9, 14]。本研究的混合原料中ZnO(MgO)与SiO2的物质的量比为1.8:1.0，即(Zn,Mg)/(Si)的比值为1.8，由图2(a)可见，在XRD灵敏度范围内，没有检测到ZnO或SiO2第二相，所有陶瓷均形成Zn2SiO4主相，这表明Mg可有效固溶在Zn2SiO4晶格中并抑制第二相的产生。从图2(b)可知，随Mg掺杂量增加，(11−3)晶面衍射峰先向高角度偏移，再向低角度偏移，而(410)衍射峰先向高角度偏移，再向低角度偏移，最后再向高角度偏移。图3所示为沿(011)晶带轴方向的Zn2SiO4晶体结构示意图。研究发现，Zn2SiO4是分别以Zn(1)、Zn(2)和 Si原子为中心的3种氧四面体形成的复杂岛状硅酸盐化合物[10]，从图3看出，Zn(1)、Zn(2)和Si分别与周围O原子键合构成Zn(1)O4、Zn(2)O4和SiO4四面体结构，四面体通过角共享形成六元环结构。衍射峰偏移方向不同是由Zn2SiO4陶瓷中六元环结构的复杂性导致的。为进一步探究Mg掺杂对 MgZn1.8-xSiO3.8陶瓷晶体结构的影响，利用 Rietveld 全谱拟合对X射线衍射数据进行精修，相关精修参数列于表1。

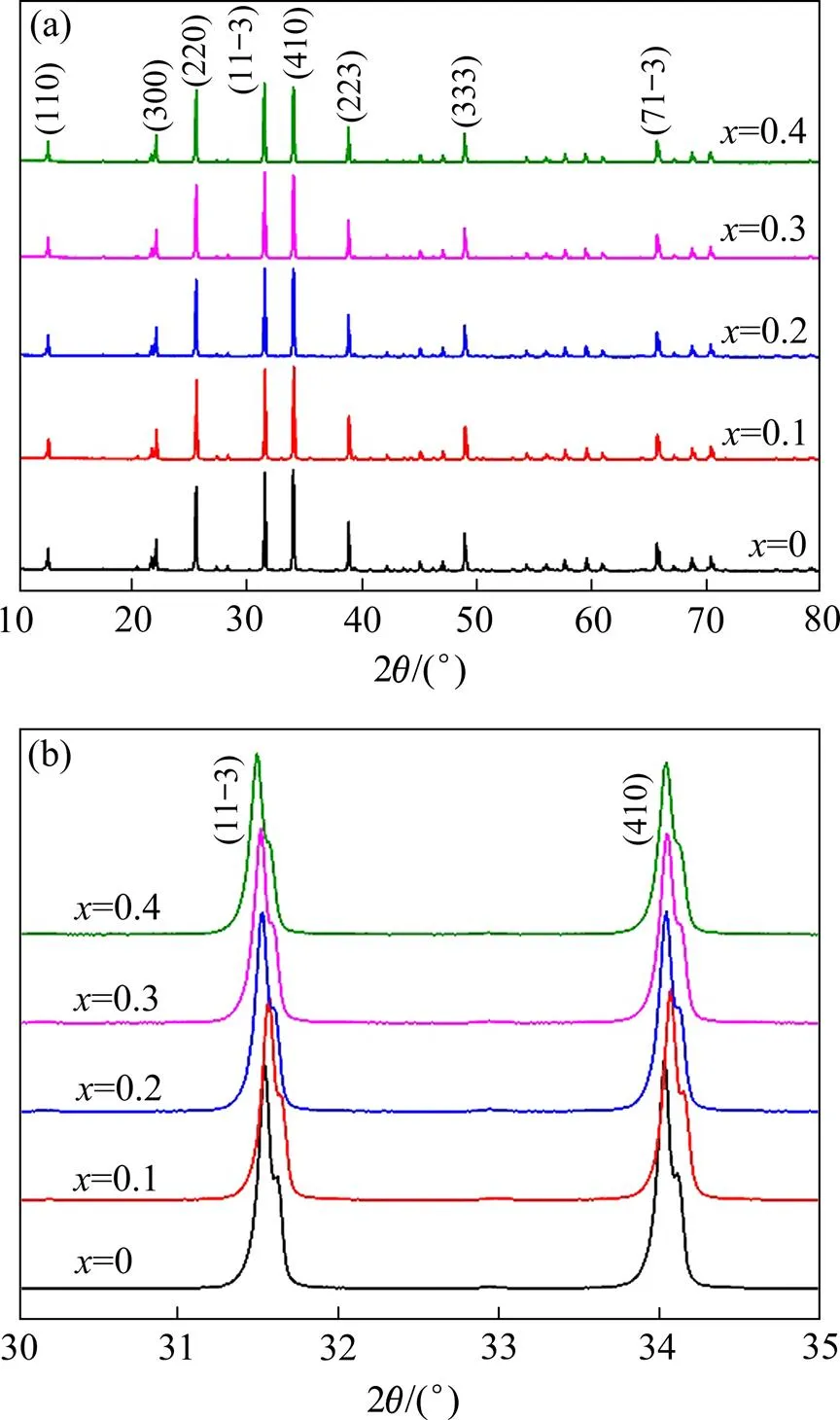
图2 MgxZn1.8−xSiO3.8陶瓷的XRD谱

(a) Overviews; (b) Enlargement of the peaks

图4所示为精修后的晶胞体积与晶格常数随掺杂量的变化。从图4(a)可知，由于Mg离子半径小于Zn离子半径(分别为 0.057 nm和0.06 nm)，所以Mg掺杂使得晶胞体积减小，并随掺杂量增加而进一步减小。晶格常数随增大而逐渐减小，表明Mg掺杂使晶胞沿轴方向收缩，这是由于离子半径较小的Mg替代离子半径大的 Zn导致的；同时，晶格常数逐渐增大，晶胞在方向和方向拉伸，这是由Zn(1)O4、Zn(2)O4、SiO4四面体组成的六元环对称性发生变化及氧四面体扭曲而导致的[18]。

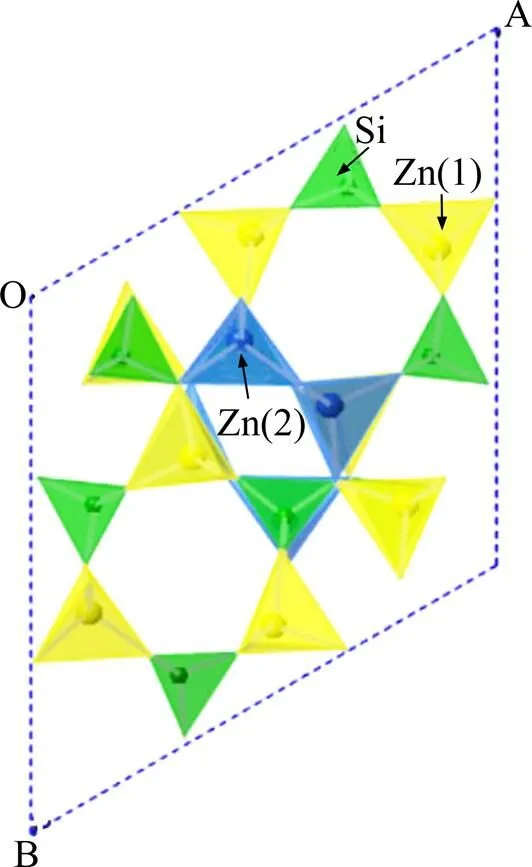
图3 沿(011)晶带轴方向的Zn2SiO4晶体结构示意图

表 1 MgxZn1.8−xSiO3.8陶瓷的Rietveld全谱拟合结构精修参数

图4 MgxZn1.8−xSiO3.8 陶瓷的晶胞参数

(a) Cell volume; (b),

图5所示为MgZn1.8−xSiO3.8陶瓷的拉曼光谱图，通过拉曼光谱可分析陶瓷晶体内部化学键的振动。已有研究表明[19]，中心位置位于800～1 100 cm−1范围内的拉曼峰对应SiO4四面体中Si－O键的拉伸，其中位于870 cm−1和908 cm−1处的峰对应Si－O键的对称伸缩振动，948 cm−1处的峰则与Si－O键的非对称伸缩振动有关[20]。中心位置位于300～700 cm−1范围内的拉曼峰对应O－Si－O键的弯曲振动，中心位置位于0～300 cm−1范围内的拉曼峰对应晶格振动。此外，中心位置位于390 cm−1处的峰对应ZnO4四面体中Zn—O键的对称伸缩振动[21]。对于二元振动，拉曼频率可用以下模型来评价[7]：

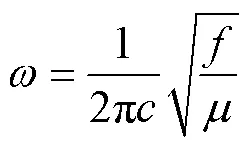
式中：为光速，为力常数，为折合质量，对于相对原子质量为1和2的原子组成的原子对，可表示为：

可由Badger定律计算：

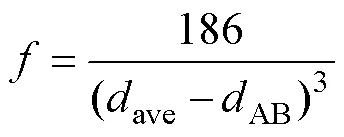
式中：ave为平均键长，AB为A－B键长。由式(2)～(4)可知，对于同种化学键，键长与拉曼频率之间呈负相关关系。图5(b)所示为中心位置的350～425 cm−1范围内的拉曼峰局部放大图，可见随Mg掺杂量增加，对应Zn(Mg)－O键的拉曼峰向高波数方向偏移，表明晶格振动逐渐减弱[22]，这是由于Mg2+离子半径小于Zn2+离子半径，随Mg2+离子含量增加，Zn(Mg)－O键长减小，键能增大，拉曼频率随之增大。

2.3 微观组织形貌

图6所示为MgZn1.8−xSiO3.8陶瓷的扫描电镜二次电子像。由图可见，在晶粒间存在少量第二相(如图中白色箭头所示)，这是由于MgZn1.8−xSiO3.8陶瓷是以非化学计量比的Zn1.8SiO3.8陶瓷为基体，与正常化学计量比Zn2SiO4基陶瓷相比存在Si过量，因此在烧结过程中出现少量液相[11]。但由于烧结完成后液相以非晶相形式存在，因此XRD中未出现第二相的衍射峰。相对于Mg、Ni掺杂的Zn2SiO4陶瓷烧结温度为1 350 ℃[12]，本研究的MgZn1.8−xSiO3.8陶瓷中少量液相的存在有利于烧结致密化，烧结温度降至1 300 ℃。

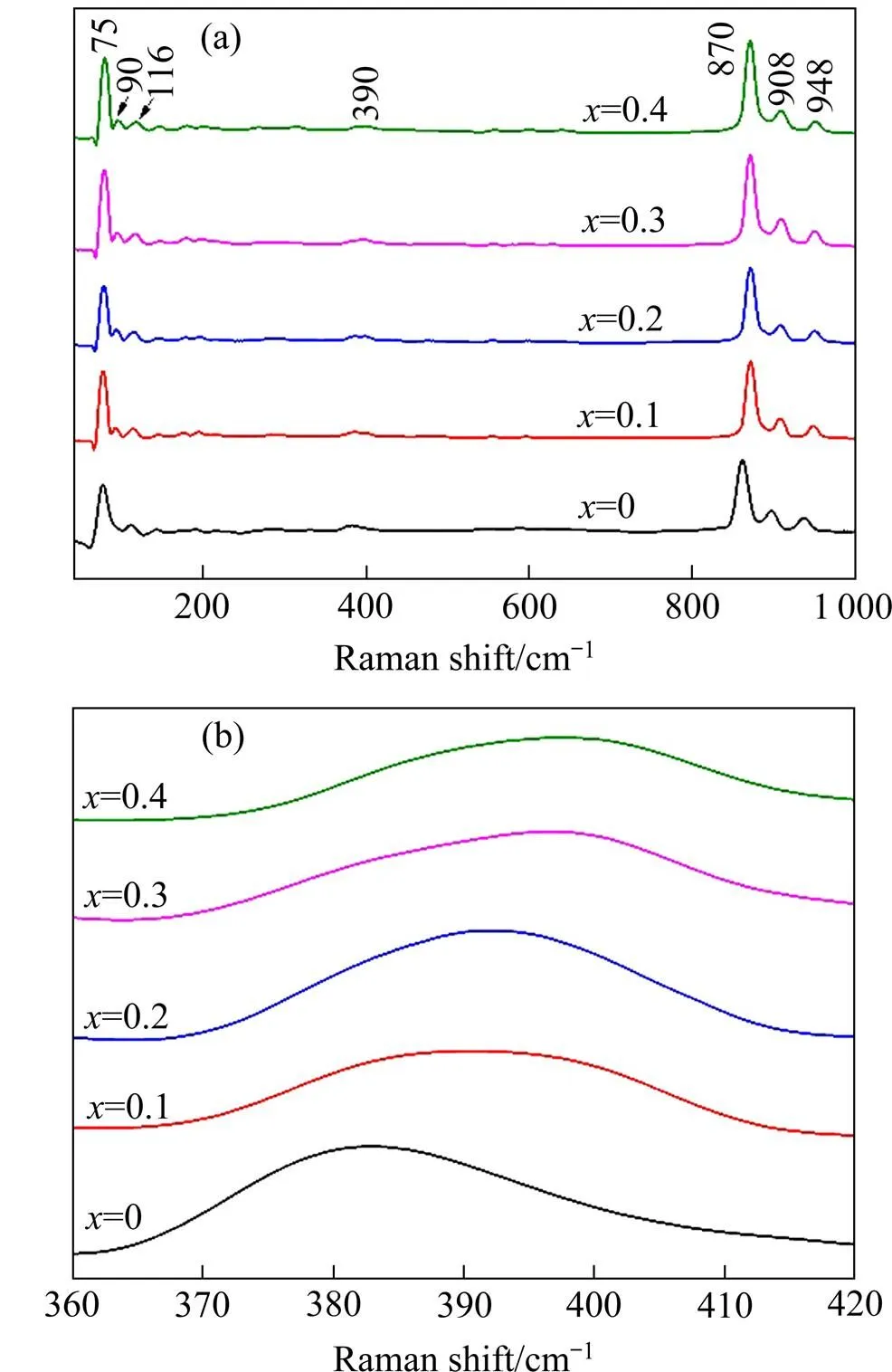
图5 MgxZn1.8−xSiO3.8陶瓷的拉曼光谱

图6 MgxZn1.8−xSiO3.8陶瓷的SEM二次电子像

(a)=0; (b)=0.1; (c)=0.2; (d)=0.3; (e)=0.4

2.4 介电性能

相对介电常数r是物质内部微观极化率的宏观表现，通常用克劳休斯−莫索缔方程(Clausius-Mosotti方程)来表示极化率与相对介电常数间的关系：

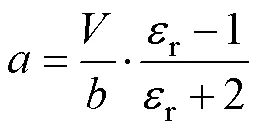
式中：为极化率，nm3；为晶胞体积，nm3；为常数；r为相对介电常数。理论离子极化率为材料各组分离子极化率之和，MgZn1.8−xSiO3.8陶瓷体系的理论极化率可用下式计算[23]：

EOH等[18]研究发现Mg掺杂能有效提高硅锌矿结构Zn1.918GeO3.918陶瓷的品质因子，随掺杂量增加，硅锌矿结构中六元环对称性增强，介电损耗随之减小；而谐振频率温度系数与氧四面体的扭曲程度有关，氧四面体扭曲程度越大，晶体结构越不稳定，进而影响谐振频率温度系数。因此在硅锌矿结构陶瓷的微波性能强烈依赖于六元环结构对称性及氧四面体畸变。氧四面体的平均扭曲度(average tetrahedral distortion)可用下式进行计算[24]：

式中：t为平均扭曲度，R为氧四面体中的单个键长，ave为平均键长。图8所示为MgZn1.8−xSiO3.8陶瓷的谐振频率温度系数f与氧四面体平均扭曲度。由图可知，随Mg掺杂量从0增加到0.4，氧四面体扭曲程度先减小后增大，谐振频率温度系数f先由−21.76× 10−6/℃减小到−18.4×10−6/℃，然后小幅增加至−19.2 ×10−6/℃。

电介质在对外加电场做出极化反应时常伴随着能量损耗，即电介质的介电损耗(tan)。对于微波陶瓷而言，常用品质因数(来表示其滤波质量，而与介电损耗tan成反比。品质因数可通过式(8)来表述：

图7 MgxZn1.8−xSiO3.8陶瓷的相对介电常数εr与理论极化率

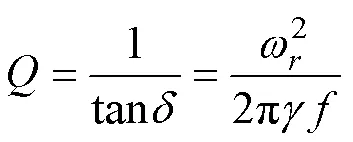
式中：ωr为材料的固有角频率，γ表示衰减系数，f为频率。由于品质因数Q与频率f乘积为定值，故常用品质因子Q×f来衡量微波陶瓷的介电损耗。图9所示为MgxZn1.8−xSiO3.8−x 陶瓷的品质因子Q×f。由图可见，随Mg掺杂量增加，陶瓷的Q×f值呈明显上升趋势。MgxZn1.8−xSiO3.8陶瓷的Q×f值与由Zn(1)/Mg(1)O4、Zn(2)/Mg(2)O4、SiO4等四面体组成的六元环对称性密切相关，六元环对称性越强，能量在离子的不断位移振动中损耗越少，Q×f值随之增大。随Mg掺杂量增加，晶胞沿a，b方向拉伸，沿c轴方向收缩，六元环对称性增强，Q×f值逐渐增加[18]。同时，由于Mg2+离子半径小于Zn2+离子半径，Mg掺杂导致Zn(Mg)—O键长减小，键能增大，从而提高晶格稳定性。因此，随Mg掺杂量增加，MgxZn1.8−xSiO3.8陶瓷的Q×f值增大。

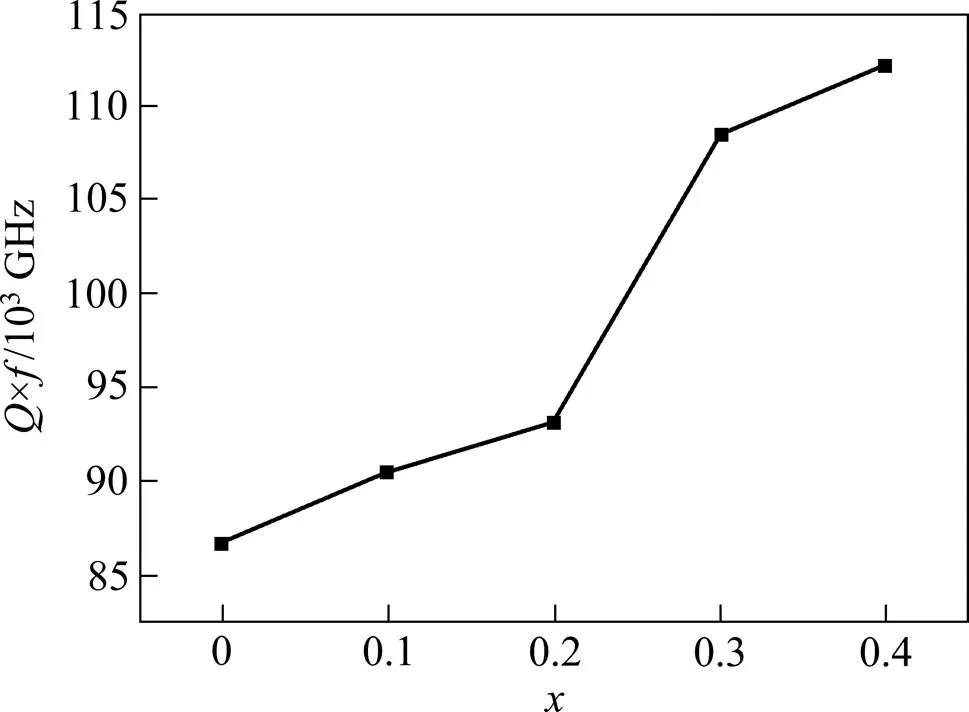
图9 MgxZn1.8-xSiO3.8陶瓷的品质因子Q×f

3 结论

1) 采用传统固相合成法制备硅锌矿结构 MgZn1.8−xSiO3.8(=0、0.1、0.2、0.3、0.4)陶瓷，在1 300 ℃烧结，Mg固溶进入Zn2SiO4晶格中，形成硅锌矿结构的Zn2SiO4主相，由于非化学计量比，烧结时出现少量液相。

2) MgZn1.8−xSiO3.8陶瓷的理论极化率随Mg掺杂量增大而减小，导致相对介电常数减小；随增大，氧四面体平均扭转度先减小后增大，相应地，谐振频率温度系数先减小再增大。随增加，由于Zn(1)/ Mg(1)O4、Zn(2)/Mg(2)O4、SiO4四面体组成的六元环对称性增强，同时Zn(Mg)—O键长减小，键能增大，导致MgZn1.8−xSiO3.8陶瓷的品质因子×值增大。

3)=0.4的Mg0.4Zn1.4SiO3.8具有较好的微波性能，×=112 100 GHz，相对介电常数r为6.2，谐振频率温度系数f为−19.2×10−6/℃。

[1] 吕学鹏, 胡杰, 张天宇. 低介电常数微波介质陶瓷研究进展[J]. 材料导报A, 2017, 31(2): 30−36.

LÜ Xuepeng, HU Jie, ZHANG Tianyu, et al. Research progress of low dielectric constant microwave dielectric ceramics[J]. Materials Reports A, 2017, 31(2): 30−36.

[2] 余海洲, 郑宇, 刘文俊. 低介电常数钒酸盐微波介质陶瓷的研究进展[J]. 中国陶瓷, 2021, 57(4): 1−8.

YU Haizhou, ZHENG Yu, LIU Wenjun, et al. Research progress of vanadate microwave dielectric ceramics with low dielectric constant[J]. China Ceramics2021, 57(4): 1−8.

[3] SYNKIEWICZ M B. Willemite with Li2CO3as a sintering aid for LTCC microwave substrates[J]. Ceramics International, 2020, 37(2): 67−72.

[4] LI S, ZHOU H, LIU X, et al. Phase evolution, microstructure, conductivity behavior and microwave dielectric properties of Li2O-2MgO-Al2O3-6MoO3ceramics[J]. Journal of Electronic Materials, 2019, 48(9): 5672−5676.

[5] TSENG C, TUNG H, HSU C, et al. Dielectric characteristics of (Mg1/2Zn1/2)Al2O4ceramics at microwave frequencies[J]. Journal of Alloys and Compounds, 2010, 502(1): 136−138.

[6] SONG X, XIE M, DU K, et al. Synthesis, crystal structure and microwave dielectric properties of self-temperature stable Ba1−xSrCuSi2O6ceramics for millimeter-wave communication [J]. Journal of, 2019, 5(4): 606−617.

[7] LAI Y, ZENG Y, HAN J, et al. Structure dependence of microwave dielectric properties in Zn2−xSiO4−xCuO ceramics[J]. Journal of the European Ceramic Society, 2021, 41(4): 2602−2609.

[8] OHSATO H, TSUNOOKA T, SUGIYAMA T, et al. Forsterite ceramics for millimeter wave dielectrics[J]. Journal of Electronic Materials, 2006, 17(2/3/4): 445−450.

[9] LiANG Z, HAN X, WANG G, et al. Microwave dielectric properties and sintering behaviors of Zn1.8SiO3.8ceramics[J]. Journal of Materials Science: Materials in Electronics, 2021, 32(1): 517−523.

[10] YE Z, LI J, WANG G, et al. Synthesis, phase composition and modified microwave dielectric properties of Mg2+substituted Zn2SiO4ceramics with uniform microstructure[J]. Materials Research Express, 2019, 6(10):106313.

[11] GUO Y, OHSATO H, KAKIMOTO K. Characterization and dielectric behavior of willemite and TiO2-doped willemite ceramics at millimeter-wave frequency[J]. Journal of the European Ceramic Society, 2006, 26(10/11): 1827−1830.

[12] TSAI W, CHIU K, NIAN Y, et al. Significant improvement of the microwave dielectric loss of Zn1.95M0.05SiO4ceramics (M = Zn, Mg, Ni and Co) prepared by reaction-sintering process [J]. Journal of Materials Science: Materials in Electronics, 2017, 28(19): 14258−14263.

[13] SONG K X, CHEN X M, ZHENG C W. Microwave dielectric characteristics of ceramics in Mg2SiO4-Zn2SiO4system[J]. Ceramics International, 2008, 34(4): 917−920.

[14] NGUYEN N H. Effect of Zn/Si ratio on the microstructural and microwave dielectric properties of Zn2SiO4ceramics[J]. Journal of the American Ceramic Society, 2010, 90(10): 3127−3130.

[15] ZHANG P, HAO M, XIAO M. Microwave dielectric properties of Li3Mg2NbO6based ceramics with (MW1−x)5+(M=Li+, Mg2+, Al3+, Ti4+) substitutions at Nb5+sites[J]. Journal of Alloys and Compounds, 2021, 853: 157386.

[16] 娄本浊. Ti-B位置换改性Mg2SiO4陶瓷微结构与微波介电性能研究[J]. 江苏陶瓷, 2008, 41(5): 8−11.

LOU Benzhuo, Microstructure and microwave dielectric characteristics of Mg2SiO4ceramics modified with Ti-substituted in B-site[J]. Jiangsu Ceramics, 2008, 41(5): 8−11.

[17] MIAO K, CAO J, XU S, et al. Microwave ceramics dielectric properties of Mg2TiO3ceramics prepared by sol-gel method from different size particles[J]. Rare Metal Materials and Engineering, 2012, 41(S3): 548−551.

[18] EOH Y J, KIM E S. High quality factor of (Zn0.6Mg0.4)1.918GeO3.918microwave dielectrics[J]. Ceramics International, 2015, 41(S1): 537−543.

[19] CHANDRA B B, RAO B V, RAVI M, et al. Structural, microstructural, optical, and dielectric properties of Mn2+: willemite Zn2SiO4nanocomposites obtained by a sol-gel method[J]. Journal of Molecular Structure, 2017, 1127: 6−14.

[20] HU G, LI W, HE G, et al. Molten salt synthesis of Zn1.8Mn0.2SiO4luminescent materials in NaCl-ZnCl2eutectic salt[J]. Ceramics International, 2016, 42(6): 7852−7856.

[21] TAGHIPOUR A H, TAHERI N E, BARI M. Effect of annealing time on structural and microwave dielectric characteristics of Li2ZnTi3O8ceramics[J]. Journal of Materials Research, 2015, 30(10): 1619−1628.

[22] 孔树, 程立金, 刘绍军. Mg4−xZnTa2O9微波陶瓷的结构和介电性能[J]. 粉末冶金材料科学与工程, 2017, 217(3): 58−63.

KONG Shu, CHENG Lijin, LIU Shaojun. Crystal structure and dielectric properties of Mg4-xZnTa2O9microwave ceramics[J]. Materials Science and Engineering of Powder Metallurgy, 2017, 217(3): 58−63.

[23] 李晶, 李昊, 刘飞, 等. Ca/Zr协同置换对CaSmAlO4基陶瓷显微结构与微波介电性能的影响[J]. 粉末冶金技术, 2021, 39(2): 127−134.

LI Jing, LI Hao, LIU Fei, et al. Effect of Ca/Zr co-substitution on microstructure and microwave dielectric characteristics of CaSmAlO4-based ceramics[J]. Powder Metallurgy Technology, 2021, 39(2): 127−134.

[24] CHENG K, LI C, YIN C. Effects of Sr2+substitution on the crystal structure, Raman spectra, bond valence and microwave dielectric properties of Ba3−xSr(VO4)2solid solutions[J]. Journal of the European Ceramic Society, 2019(13): 3738−3743.

Structure and properties of MgZn1.8−xSiO3.8microwave ceramics with low dielectric constant

DUAN Jialu, ZHOU Ganghuai, LIU Shaojun

(State Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China)

MgZn1.8−xSiO3.8(=0, 0.1, 0.2, 0.3, 0.4) microwave ceramics with willemite structure were prepared by the traditional solid-phase synthesis method. The effect of Mg on crystal structure, microstructure and dielectric properties of MgZn1.8−xSiO3.8−xceramics were characterized on the basis of X-ray diffraction, raman spectroscopy, and scanning electron microscopy and vector network analyzer. The results show that the theoretical polarizability of MgZn1.8−xSiO3.8microwave ceramics decreases, and the relative permittivity decreases correspondingly with the increase of doping Mg amountof sintering temperature at 1 300 ℃. With the increase of, the average twist of oxygen tetrahedron decreases first and then increases, resulting in the temperature coefficient of resonant frequency decreasing first and then increasing. With the increase of doping amount, the symmetry of the six-membered ring composed of Zn(1)/Mg(1)O4, Zn(2)/Mg(2)O4, and SiO4tetrahedra increases, while the Zn(Mg)—O bond length decreases and the bond energy increases, resulting in the quality factor×increases. Mg0.4Zn1.4SiO3.8ceramicshave excellent properties, the relative permittivityris about 6.2, the×is about 112 100 GHz, and the resonant frequency temperature coefficientfis about −19.2×10−6℃.

low dielectric constant; microwave ceramics; doping; crystal structure; dielectric property

10.19976/j.cnki.43-1448/TF.2022005

TB34

A

1673-0224(2022)03-276-08

湖南省自然科学基金资助项目(2021JJ30831)

2022−01−26；

2022−03−11

刘绍军，教授，博士。电话：13974953502；E-mail: liumatthew@csu.edu.cn

(编辑 汤金芝)