基于直觉模糊集和区间值模糊集模糊推理算法的关系

史宏艳,罗敏霞

(中国计量大学 理学院,浙江 杭州 310018)

模糊推理基本的推理形式是模糊取式(fuzzy modus ponens,FMP)和模糊拒取式(fuzzy modus tollens,FMT):

FMP:输入A*,和模糊规则“如果A,则B”,然后推断出一个合理的输出B*;

FMT:输入B*,和模糊规则“如果A,则B,然后推断出一个合理的输出A*。

Zadeh在文献[1]给出合成推理规则(compositional rule of inference,CRI)来解决上述问题。然而,研究发现该算法运用复合运算,使用的三角范数没有对应的蕴含算子,即运用的算子具有随机性,缺乏严格的逻辑基础,针对这一缺陷,Wang在文献[2]给出全蕴涵三I方法改进传统的CRI算法。此后,许多学者对三I方法进行了一系列研究,并取得了大量成果。文献[3]给出三I算法的统一形式。文献[4]讨论了模糊推理全蕴涵三I算法的连续性。

虽然模糊集已经成功应用于许多领域,但在描述信息的模糊性和不确定性方面仍然存在一些缺陷。所以Zadeh引入区间值模糊集[5]。随着区间值模糊集的提出,许多学者做了大量的理论算法研究并且广泛应用于各个领域。文献[6]研究了具有多个先行规则的区间值模糊推理算法。文献[7]研究区间值模糊推理CRI方法的鲁棒性。文献[8-10]分别将模糊推理全蕴涵、五蕴涵和相似度算法推广到区间值模糊集并取得了相关的研究成果。

直觉模糊集[11]作为模糊集的另一个扩展,迄今为止,对直觉模糊集的推理算法研究已经取得了很多研究成果。文献[12-13]将CRI方法、三I方法推广到直觉模糊集上。文献[14]利用构造的相似度讨论直觉三I算法的鲁棒性。

虽然在区间值模糊集与直觉模糊集的推理算法上取得大量研究成果,但这些推理算法之间的关系尚未得到研究。因此本文研究基于这两种模糊集的推理算法之间的关系。

1 预备知识

定义1.1[15]若映射T:[0.1]2→[0,1]满足交换律、结合律、单调性和边界条件,即T(x,1)=x,则T称为三角范数。若映射S:[0.1]2→[0,1]满足交换律、结合律、单调性和边界条件,即S(0,x)=x,则S称为三角余范。

定义1.2[15]若一个三角范数T,对任意的(x0,y0)∈[0,1]2,ε>0,存在δ>0,使得(x,y)∈(x0-δ,x0]×(y0-δ,y0]时,有T(x,y)>T(x0,y0)-ε成立,则T称为左连续的。

定义1.3[16]对任意a,b∈[0,1],设T是左连续三角范数,则T诱导的剩余蕴涵R为:

R(a,b)=sup{x∈[0,1]|T(a,x)≤b}。

例1.1[17]ukasiewicz三角范数TL及其剩余蕴涵RL:

TL(a,b)=(a+b-1)∨0,

RL(a,b)=(1-a+b)∧1。

定义1.4[11]非空论域X上的直觉模糊集定义为:

A={(x,μA(x),νA(x))|x∈X},

且μA(x)∈[0,1],νA(x)∈[0,1](0≤μA(x)+μA(x)≤1)

在本文中,我们用IFS(X)表示论域X上的所有直觉模糊子集的集合。设A,B∈IFS(X),包含、并和交运算关系定义如下:

1)A⊆B成立当且仅当μA(x)≤μB(x),νA(x)≥νB(x);

2)A∪L*B={(x,sup(μA(x),μB(x)),inf(νA(x),νB(x))|x∈X};

3)A∩L*B={(x,inf(μA(x),μB(x)),sup(νA(x)νB(x))|x∈X}。

设L*={(x1,y1)|(x1,y1)⊆[0,1]2,x1+y1≤1},在L*上序的关系定义为:如果x1≤x2,y1≥y2,则(x1,y1)≤L*(x2,y2)。此外,(x1,y1)∧L*(x2,y2)=(x1∧x2,y1∨y2),(x1,y1)∨L*(x2,y2)=(x1∨x2,y1∧y2).对于任意的(xi,yi)∈L*,sup(xi,yi)=(supxi,infyi),inf(xi,yi)=(infxi,supyi).L*上的最大、最小元分别是1*=(1,0)和0*=(0,1),容易证明(L*,∧L*,∨L*,0*,1*)是完备格[18]。

定义1.5[19]若映射TT,S:L*×L*→L*满足交换律、结合律、单调性和边界条件,即对于任意的x∈L*,满足TT,S(x,1*)=x,则TT,S称为直觉三角范数。

例1.2[19]若映射TT,S:L*×L*→L*满足TT,S((a1,a2),(b1,b2))=(T(a1,b1),S(a2,b2)),其中S为三角范数T对应的三角余范,则TT,S称为相关联的直觉三角范数。

如果T是左连续的三角范数且S为三角范数T对应的右连续的三角余范,则相关联的直觉三角范数TT,S是左连续的。

定义1.6[19]由左连续的相关联直觉三角范数TT,S诱导的直觉剩余蕴涵RT,S定义为

RT,S(a,b)=sup{η∈L*}|TT,S(η,a)≤b}。

引理1.1[13]设R为三角范数T诱导的剩余蕴涵,直觉剩余蕴涵RT,S有如下表现形式:

RT,S((a1,a2),(b1,b2))=(R(a1,b1)∧R(1-a2,1-b2),1-R(1-a2,1-b2))。

定义1.7[5]非空论域X上的区间值模糊集定义为BT,T={(x,[Bl(x),Br(x)])|[Bl(x),Br(x)]⊆[0,1],x∈X},在本文中,我们用IVFS(X)表示论域X上的所有区间值模糊子集的集合。设AT,T,BT,T∈IVFS(X),包含、并和交运算关系定义为:

1)AT,T⊆BT,T成立当且仅当Al(x)≤Bl(x),Ar(x)≤Br(x);

2)AT,T∪LIBT,T={(x,[sup(Al(x),Bl(x)),sup(Ar(x),Br(x))])|x∈X};

3)AT,T∩LIBT,T={(x,[inf(Al(x),Bl(x)),inf(Ar(x),Br(x))])|x∈X}。

设LI={[x1,y1]|[x1,y1]⊆[0,1],x1≤y1},在LI上序的关系定义为:如果x1≤x2,y1≤y2,则[x1,y1]≤LI[x2,y2],此外,[x1,y1]∧LI[x2,y2]=[x1∧x2,y1∧y2],[x1,y1]∨LI[x2,y2]=[x1∨x2,y1∨y2].对于任意的[xi,yi]∈LI,sup[xi,yi]=[supxi,supyi],inf[xi,yi]=[infxi,infyi].LI上的最大、最小元分别是1I=[1,1]和0I=[0,0],容易证明(LI,∧LI,∨LI,0I,1I)是完备格[20]。

定义1.8[19]若一个映射TT,T:LI×LI→LI满足交换律,结合律,单调性和边界条件TT,T(x,1I)=x,则TT,T称为区间值三角范数。

例1.3[21]若映射TT,T:LI×LI→LI满足TT,T((a1,a2),(b1,b2))=[T(a1,b1),T(a2,b2)],T为三角范数,则TT,T称为相关联区间值三角范数。

如果T是左连续的三角范数则相关联区间值三角范数TT,T是左连续的。

定义1.9[22]设TT,T是左连续的相关联区间值三角范数,则TT,T诱导的区间值剩余蕴涵RT,T定义为

RT,T(a,b)=sup{η∈LI|TT,T(η,a)≤b}。

引理1.2[22]设R为三角范数T诱导的剩余蕴涵,区间值剩余蕴涵RT,T有如下表现形式:

RT,T((a1,a2),(b1,b2))=[R(a1,b1)∧R(a2,b2),R(a2,b2)]。

引理1.3[23]设映射g:IFS(X)→IVFS(X),AB定义如下:

A={(x,μA(x),νA(x))|x∈X},B={(x,[μA(x),1-νA(x)])|x∈X},则格(IFS(X),∪L*,∩L*)和(IVFS(X),∪LI,∩LI)是同构的。

2 基于直觉模糊集和区间值模糊集全蕴涵三I算法的关系

定义2.1[13]直觉模糊推理全蕴涵三I模型:

RT,S(RT,S(A(x),B(y)),RT,S(A*(x),B*(y)))。

(1)

其中A,A*∈IFS(X),B,B*∈IFS(Y),且RT,S是由左连续相关联的直觉三角范数TT,S诱导的直觉剩余蕴涵,如果在论域Y(或X)上存在最小(大)的直觉模糊集B*(或A*)使得(1)达到最大值,则B*(或A*)称为求解直觉FMP(FMT)(记为IFMP(IFMT))问题的全蕴涵三I算法解。

定理2.1[13]设RT,S是由左连续的相关联直觉三角范数TT,S诱导的直觉剩余蕴涵,则

1)求解IFMP问题的三I算法解为

2)求解IFMT问题的三I算法解为

定义2.2[24]区间值模糊推理全蕴涵三I模型:

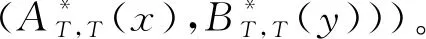
(2)

定理2.2[24]若RT,T是由左连续的相关联区间值三角范数TT,T诱导的区间值剩余蕴涵,则

1)求解IVFMP问题的三I算法解为

2)求解ZVFMT问题的三I算法解为

定理2.3若RT,S是由左连续的相关联直觉三角范数TT,S诱导的直觉剩余蕴涵,RT,T是由左连续的相关联区间值三角范数TT,T诱导的区间值剩余蕴涵,则剩余格(IFS(X),∩L*,∪L*,0*,1*,TT,S,RT,S)和剩余格(IVFS(X),∩LI,∪LI,0I,1I,TT,T,RT,T)是同构的。

证明:设映射g:IFS(X)→IVFS(X),(x1,x2)[x1,1-x2],根据引理1.3可得(IFS(X),∩L*,∪L*,0*,1*)≅(IVFS(X),∩LI,∪LI,0I,1I).

对于任意的m=(x1,x2),n=(y1,y2),可得，

g(TT,S(m,n))=

g(TT,S((x1,x2),(y1,y2)))=

g(T(x1,y1),S(x2,y2))=

[T(x1,y1),1-S(x2,y2)]=

[T(x1,y1),1-(1-T(1-x2,1-y2))]=

[T(x1,y1),T(1-x2,1-y2)]=

TT,T([x1,1-x2],[y1,1-y2])=

TT,T(g(x1,x2),g(y1,y2))=

TT,T(g(m),g(n)),

g(RT,S(m,n))=

g(RT,S((x1,x2),(y1,y2)))=

g(R(x1,y1)∧R(1-x2,1-y2),

1-R(1-x2,1-y2))=

[R(x1,y1)∧R(1-x2,1-y2),

R(1-x2,1-y2)]=

RT,T([x1,1-x2],[y1,1-y2])=

RT,T(g(x1,x2),g(y1,y2))=

RT,T(g(m),g(n))。

证明:设映射g:IFS(Y)→IVFS(Y),(y1,y2)[y1,1-y2]。

对于任意的m=(x1,x2),n=(y1,y2)

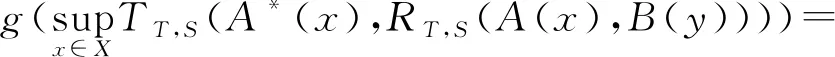
证明:设映射g:IFS(X)→IVFS(X),(x1,x2)[x1,1-x2]。

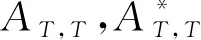
表1 A,A*和B的数据

表和BT,T的数据

表3 IFMP算法解B*和IVFMP算法解

表4 映射g作用下的B*对应的C值

3 结 论

本文研究了直觉模糊推理方法与区间值模糊推理方法之间的关系。证明了直觉模糊推理全蕴涵三I算法解与区间值模糊推理全蕴涵三I算法解是一一对应的关系。从数学的角度,证明了基于这两个模糊集的推理算法在本质上是等价的。然而,这两种方法都有各自的优点。在实际应用中,区间值模糊集可以有效减少模糊信息的损失,直觉模糊集可以从两个方面表征信息。直觉模糊推理方法和区间值模糊推理方法将在许多领域得到应用。