双激励十字型斜槽式纵扭复合振动压电超声换能器的设计

张 丹,许 龙,张海岛,高 敏

(中国计量大学 理学院,浙江 杭州 310018)

功率超声振动系统以其工艺简单、性能可靠、环保节能等优点，在超声清洁、超声马达、废水处理等领域得到广泛的应用[1-3]。然而,随着超声技术的发展,对超声技术的要求也越来越多样化,超声复合振动系统逐渐成为研究的热点。研究表明,复合振动模式下的超声切削与超声焊接能获得优于传统单一振动超声加工的工件表面质量及加工效率[4-5],被广泛适用于碳纤维、结构陶瓷等硬脆材料的超声加工[6-7]。

复合超声振动包括纵扭复合振动[8-9],纵弯复合振动[10]以及扭转弯曲复合振动[11]等。目前,实现纵扭复合超声振动的方法主要有:推挽式振动装置[12]、切向极化压电换能器[13]、螺旋沟槽式振动装置[14]、斜槽式纵扭振动装置[15]等。推挽式纵扭振动装置的功率可以很大,但纵-扭振动之间转换效率不高。切向极化压电换能器的理论设计成熟,但切向极化压电晶片的制作工艺复杂,很难研制出高性能的纵扭复合振动换能器。螺旋沟槽式振动装置的理论设计和计算比较复杂,不利于一般的工程设计应用。斜槽式纵扭振动装置通过对系统结构进行开槽或狭缝从而实现振动模式的转换,结构简单,振动模式容易简化合并,可用单相电源激励,在工程技术领域的应用越来越受到重视。但目前斜槽式纵扭振动装置仅能实现一维复合振动,随着超声应用对超声换能器各项性能参数要求的提高,如何实现多维纵扭超声辐射成为纵扭复合换能器亟需解决的关键技术问题。

本文基于对斜槽式纵扭复合振动装置的研究,设计了一种双激励十字型斜槽式纵扭复合振动压电超声换能器,使两组压电陶瓷晶堆协同工作,利用二维振动耦合与斜槽式纵扭振动模式转换原理,实现了y方向纵向超声振动激发和x方向的双向纵扭复合超声振动输出,使换能器具有大功率和二维双向纵扭复合超声振动输出特性,有助于解决现有纵扭复合超声换能器的功率容量较小和超声作用方向单一的不足,实现对现有的纵扭复合超声换能器的结构和振动性能的改进和提高。基于机电类比原理,建立了换能器的等效电路模型与共振频率方程。利用所得的共振频率方程解析计算了不同斜槽位置的双激励十字型斜槽式纵扭复合振动压电超声换能器的谐振频率,得到的结果与有限仿真得到的计算值基本吻合。同时,利用有限元法探讨了斜槽参数对换能器振动性能的影响特性。本文提出的双激励十字型斜槽式纵扭复合振动压电超声换能器有望在机器人关节[16]、多维超声旋转加工[17]、多维超声电机[18-19]等领域得到应用。

1 双激励十字型斜槽式纵扭复合振动压电超声换能器的结构与工作原理

图1为双激励十字型斜槽式纵扭复合振动压电超声换能器的几何示意图,该换能器由一个中心耦合立方体金属块、两组分别由两片压电陶瓷环片组成的压电陶瓷晶堆、四个外部金属圆柱前盖板和两根传振杆组成。a为中心耦合立方体金属块的边长,Lf为y轴方向压电陶瓷端外接的实心金属圆柱前盖板的长度,Lc为x轴方向两个外接实心金属圆柱前盖板的长度,Lm为空心传振杆的长度,四根金属圆柱的径向尺寸、压电陶瓷片的径向尺寸和传振杆的外径均与中心耦合块的边长相等。

图1 双激励十字型斜槽式纵扭复合振动压电超声换能器的几何示意图

图2为斜槽式传振杆的几何示意图。其内外半径分别为R1和R2,其中R2=a/2,斜槽与传振杆轴线的夹角为θ,斜槽前传振杆的长度为L1,其余部分的长度为L2。斜槽能将部分正应力转换为切应力,从而将纵波转换为横波,实现波的模式转换,继而产生扭转振动。近似认为L1部分的振动只有纵向振动,而L2的振动是纵向扭转复合振动[20]。为了简化计算,假定斜槽的宽度无限小,不影响换能器的质量,仅仅起到将纵向振动转变为扭转振动的作用。

图2 斜槽式传振杆的几何示意图

2 双激励十字型斜槽式纵扭复合振动压电超声换能器的等效电路

如图3,双激励十字型斜槽式纵扭复合振动压电超声换能器可以看作是由一个双激励L-L型夹心式压电激励器和两根斜槽式传振杆两部分组成,分别推出各部分的机电等效电路,利用换能器各组成部分机械上串联,电路上并联的连续边界条件,可得换能器整体振动的机电等效电路如图4。

图3 双激励十字型斜槽式纵扭复合振动压电超声换能器的结构模型图

其中,双激励L-L型夹心式压电激励器[21]由中心耦合质量块、压电陶瓷晶堆和四根外接金属圆柱前盖板组成。中心耦合质量块与压电陶瓷晶堆的等效电路分别如图4中Ⅰ、Ⅱ部分所示,y轴方向两个外接实心金属圆柱前盖板如图4中Ⅲ部分所示,x轴方向两个外接实心金属圆柱前盖板如图4中Ⅳ部分所示。各部分参数表达式分别为:

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

其中,Z0C=ρC·cC·SC,kC=ω/CC,Z0P,Z0Y,Z0X的表达式与Z0C形式相同,kP,kY,kX的表达式与kC形式相同,只需将C置换为P,Y,X即可。ρ,c和S分别表示为各部分组成材料的密度、纵波声速和横截面积。各参数下标C,P,Y和X分别表示：中心耦合质量块,压电陶瓷晶堆,y轴方向两个外接实心金属圆柱前盖板与x轴方向两个外接实心金属圆柱前盖板的材料参数。

对于斜槽式传振杆部分,其等效电路如图4的Ⅴ部分所示[15],各参数表达式分别为:

(9)

(10)

(11)

(12)

(13)

(14)

基于传输线路阻抗转移公式理论,可得传振杆输入端的机械输入阻抗Zi为:

Zi=jZ1tan(k1L1+α),

(15)

(16)

(17)

图4 双激励十字型斜槽式纵扭复合振动压电超声换能器的等效电路

通过传输线阻抗转移理论,可得双激励十字型斜槽式纵扭复合振动压电超声换能器的等效输入阻抗为

(18)

其中,

(19)

(20)

(21)

(22)

(23)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

当换能器的输入阻抗值为零时,可得到其谐振频率方程:

Zem=0。

(33)

3 数值仿真

图5 双激励十字型斜槽式纵扭复合振动压电超声换能器的纵扭振动模态Figure 5 Longitudinal torsional vibration mode diagram of dual-excited cross-shaped longitudinal-torsional composite vibration piezoelectric ultrasonic transducer with slanting slots

为了对比等效电路法与有限元法得出的结果,验证上文所提等效电路的可行性,分别用两种方法计算了不同斜槽位置的换能器的共振频率,计算结果如表1。在表1中,fm与fc分别表示等效电路法与有限元软件所得的换能器纵扭振动共振频率,相对误差Δ=|fm-fc|/fc。

表1 换能器的共振频率随L1的变化关系

4 分析讨论

由表1可见,等效电路法的计算结果与有限元仿真模拟结果基本一致,相对误差介于2.44%～4.13%之间,符合工程设计应用的要求,且换能器的共振频率随L1的增大而增大。由图5可见,该换能器利用纵向振动的耦合与振动模式的转换,很好地实现了多方向纵扭复合振动,有助于解决现有纵扭复合超声换能器存在的超声作用方向单一、超声辐射面积有限的不足。

有效机电耦合系数是反映换能器机电转换性能的重要参数,为了分析斜槽位置对换能器的有效机电耦合系数的影响规律,分别利用有限元法与等效电路法计算了不同斜槽位置换能器的有效机电耦合系数,结果如图6。可以看出,保持斜槽式传振杆的长度一定,随着L1的逐渐增大,换能器的有效机电耦合系数逐渐降低。由此可见,该换能器在合理设计结构尺寸时,可以实现双向纵扭复合振动的输出,也可以获得较高的机械转换效率。

图6 斜槽位置对有效机电耦合系数的影响规律

为了进一步分析斜槽结构参数对换能器振动性能的影响规律,设定传振杆输出端扭转与纵向幅值的比值为扭纵比,利用有限元法分别计算了斜槽角度、斜槽数量和斜槽长度对换能器的纵扭比的影响规律,结果分别如图7(a)、(b)和(c)。由图7可知,随着斜槽角度、斜槽数量和斜槽长度的增加,扭纵比均呈现逐渐增加的趋势,这是因为斜槽的角度、数量、长度参数会直接影响传振杆中斜槽能吸收纵波的横截面积,斜槽的截面积越大,则能吸收的纵波越多,从而产生更大的切向力分量,使扭转振动的幅度相应增加。

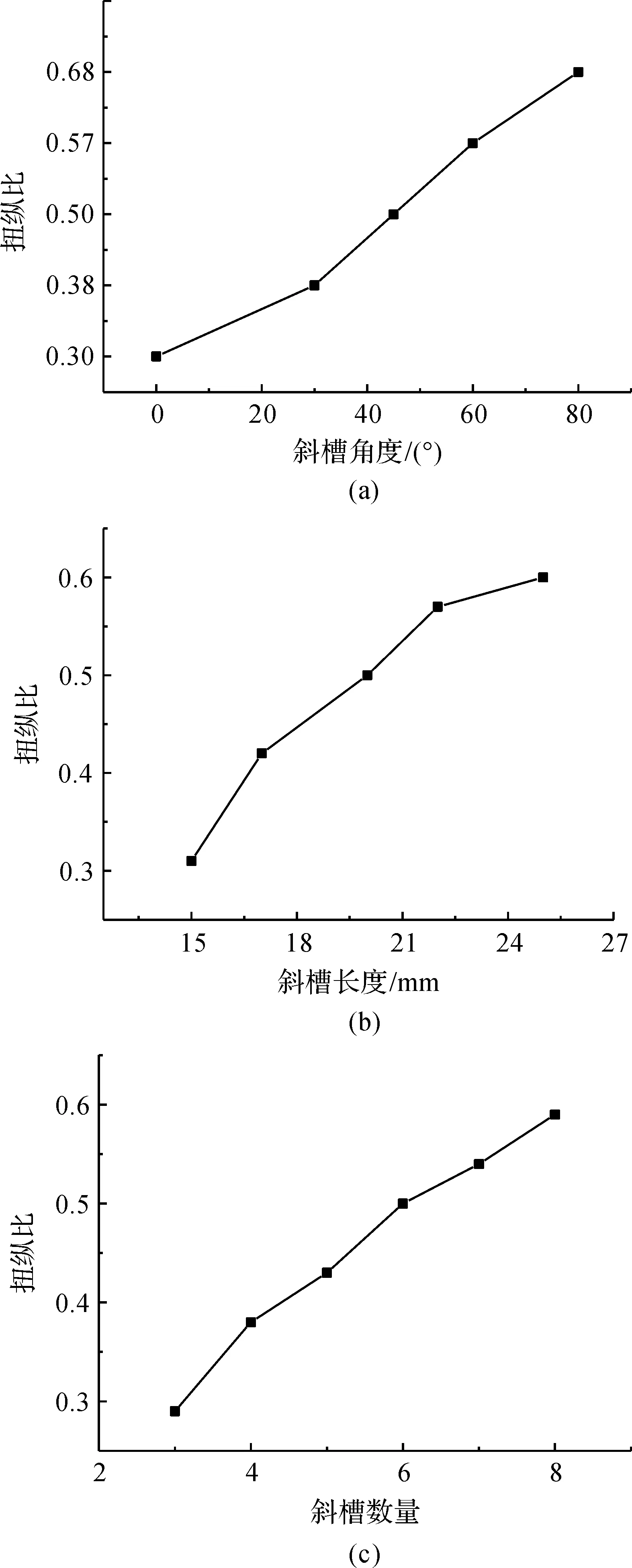
图7 斜槽各参数对扭纵比的影响规律

5 结 语

本文提出了一种双激励十字型斜槽式纵扭复合振动压电超声换能器,建立了其机电等效电路模型与共振频率方程,并通过模拟得到了换能器的振动模态图,探讨了斜槽参数对扭纵比的影响。研究表明,理论计算结果与仿真结果吻合较好,且换能器输出端的扭纵比随斜槽长度、角度与数量的增大而增大。本文提出的换能器利用二维振动耦合与斜槽式纵扭振动模式转换原理,实现了y方向纵向超声振动激发和x方向的双向纵扭复合超声振动输出,使换能器具有大功率和二维双向纵扭复合超声振动输出特性,这有助于解决现有纵扭复合超声换能器的功率容量较小和超声作用方向单一的不足,可望在超声马达、多维超声电机、多维超声旋转加工等行业获得重要应用。