基于岩石微破裂演化崩塌失稳预警室内试验研究

2022-07-18陈世万杨根兰

矿业安全与环保 2022年3期

杨贵，陈世万，余琪，杨根兰

(1.贵州大学资源与环境工程学院，贵州贵阳 550025； 2.喀斯特地质资源与环境教育部重点实验室, 贵州贵阳 550025)

采矿活动是诱发岩体崩塌的最主要因素，如 2017年8月发生的纳雍县张家湾镇普洒村的岩体崩塌，造成 26人遇难，9人失踪，主崩塌体失稳仅用时26 s，研究发现，该崩塌与煤矿地下采矿活动密切相关[1-2]。当前，一些学者针对岩体崩塌监测预警开展了广泛的研究。陈洪凯等[3]对拉剪型危岩发育过程进行了室内模拟试验研究，得出了拉剪型危岩在初期以张拉破坏为主，临近破坏时以剪切破坏为主的结论;唐红梅等[4]通过相似模型试验探讨了边坡开挖过程中的应力与位移变化规律，提出了岩质边坡以三维应力监测为主、位移监测为辅的监测优化方案。但是岩体崩塌的加速蠕变过程具有快速性和突发性，以监测变形为主的方法难以对岩体崩塌做到有效预警。鉴于此，杜岩等[5-6]进一步研究了基于动力学监测指标计算危岩体力学参数的方法，并应用固有振动频率对岩体损伤进行动态识别和定量判断。

实际上，岩体崩塌就是岩体内部裂纹扩展直至形成贯通面的过程，在岩石内部裂纹扩展过程中会有能量释放并伴随着弹性波的产生，释放的低频和高频弹性波分别为微震和声发射信号。微震技术已被广泛应用于岩石工程中，如冯夏庭等[7]应用微震监测分析了锦屏Ⅱ级水电站引水隧洞发生的即时型岩爆和时滞型岩爆的信号特征；DAI Feng等[8]分析了多个微震参数的演化规律，得出围岩大变形前的前兆信息；王创业等[9]通过获取花岗岩单轴压缩变形破裂全过程声发射时频域信号信息，结合频谱分析理论探讨了主频的演化规律；甘一雄等[10]通过花岗岩巴西劈裂试验，探讨了基于声发射RA(上升时间/振幅)与 AF(平均频率)值的参数指标描述岩石破坏剧烈程度的可行性与优势；李建功[11]深入研究了声发射传感器原位安装方法，并实现了对煤岩破裂信号的实时监测；潘懿等[12]研究了岩石单轴压缩试验的声发射事件率、声发射波形特征等参数的变化规律，认为声发射事件率的迅速增加、振幅的增大可作为岩石破坏的预警指标。

近年来，国内外学者也开展了微震监测在岩体崩塌监测方面的研究。李庶林等[13]通过矿山微震监测系统分析了某次爆破产生的山体崩塌的微震信号，认为崩塌前的剪切破裂信号可作为前兆信息；FENG L等[14]探讨了岩体破坏前落石撞击、弹跳和滚动累计能量等参数的变化规律，并基于此成功预警一次较大规模的崩塌；DIETZE M等[15]研究了微震定位岩质陡坡崩塌的准确性，并分析了崩塌发生过程中岩块崩落、撞击、碎裂和堆积过程中的微震信号特征；SENFAUTE G等[16]将危岩各个发育阶段与落石前15 h的微震频率特征相联系，判定微震信号频率突降可作为危岩失稳前兆参量。

为全面获得裂纹发展全过程低频和高频信号，同时验证专门针对岩体崩塌监测研发的无线微震传感器的可靠性，笔者采用无线微震监测与声发射监测系统监测裂纹发展过程的声信号；通过分级蠕变加载的方式，开展室内岩体崩塌模拟试验，对采集到的信号，采用自适应噪声完全集合经验模态分解(CEEMDAN)与小波相结合的联合去噪方法，获取岩石破裂全过程的信号，在此基础上，分析其时域波形参数(幅值、累计撞击数)和频域特征，提取前兆信息。

1 试验设备与方法

1.1 试样准备及试验设备

1.1.1 试样准备

试样由白云岩加工制作而成，原岩为贵州西北部寒武系白云岩，天然状态下呈灰白色，质地均匀，无肉眼可见裂纹。试样整体为140 mm×140 mm×50 mm的长方体样(见图1)，预制“凹岩腔”平面尺寸为直径50 mm的圆形，裂纹深度为25 mm。试样均取自于同一块原岩，尺寸误差小于2 mm。

图1 试样照片

1.1.2 试验设备

为排除压力机加载过程中产生的干扰信号，自主改造设计分级蠕变加载试验机，试验机为杠杆砝码加载式，杠杆比为12∶1，可提供最大10 kN荷载，满足本试验加载需求。监测系统为专门研发的无线微震监测系统，经实际工程及室内试验得出，本次试验采样频率设置为500 Hz，声发射监测仪器为美国PCI-2E5.40声发射监测系统，国产探头型号为PXR15M，中心频率为150 kHz。

1.2 试验方法

1)概化拉剪型岩体崩塌模型，并采用白云岩预制“凹岩腔”和裂纹，以此模拟张拉型岩体崩塌发育形态。

2)分级蠕变加载。为研究拉剪型岩体崩塌微震和声发射信号波形参数特征和频域特征，分为三级加载方式进行，基于线弹性断裂力学理论，根据试样I型裂纹断裂韧性，设计分级加载的荷载分别为1.2、1.5、1.8 kN。

3)试验数据采集。微震、声发射、应变片及位移传感器布置如图2所示。

图2 室内模拟试验装置

2 微震信号处理方法

2.1 微震信号识别

微震数据采集过程中放大器等不可避免地会产生电磁白噪声，采用谱熵法来判别白噪声与微震信号。谱熵是由香农熵发展而来的，广泛应用于故障检测、语音信号端点检测等信号识别领域[17-18]。白噪声与微震组合波形及谱熵图如图3所示。

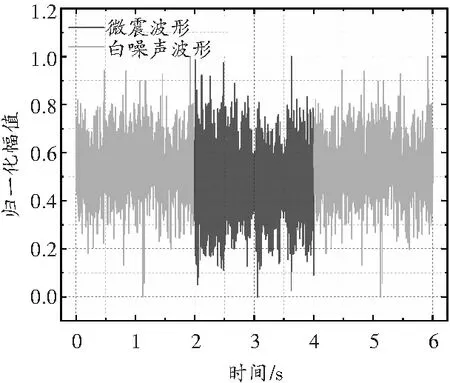
(a)组合信号

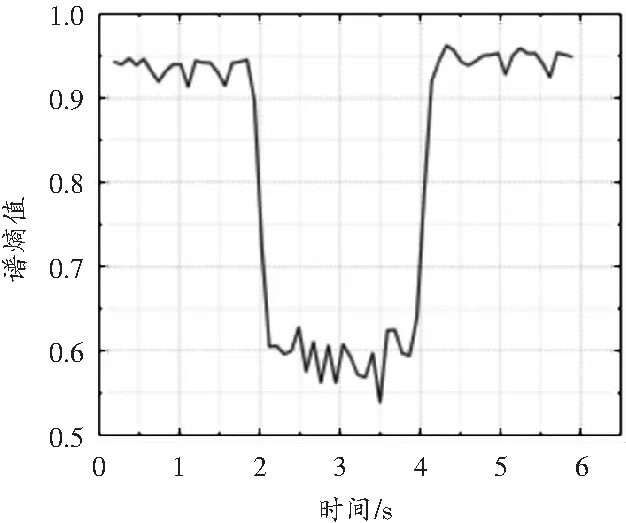
(b)组合信号谱熵图

将白噪声与微震信号组合在一起,利用谱熵检测微震信号的存在位置(见图3(a))。计算微震信号、白噪声和组合信号的谱熵值分别为0.595 8、0.997 5、0.617 1。由图3(b)可知，在白噪声序列的中间含有微震信号的区域，谱熵明显降低。这是因为微震信号的出现使得这段信号的不确定性下降所致。故判定该信号为微震信号，而非白噪声。

2.2 微震信号去噪

经过以上步骤，并不能剔除叠加在微震信号中的噪声，故还需对信号进行降噪处理。目前常用的信号滤波方法有傅里叶变换滤波、小波包滤波、小波阈值滤波，以及经验模态分解等[19]。小波分析去噪效果较好，但容易造成信号失真。相比小波分析，经验模态分解更具有自适应性，但会产生模式混叠现象[20-21]。故结合两者的优点，将自适应噪声完全集合经验模态分解(CEEMDAN)和小波分析相结合，以此对微震信号进行去噪处理。

2.2.1 CEEMDAN原理

CEEMDAN方法是对EEMD的改进，此方法不仅能降低经验模态分解(EMD)的模态混叠程度，更能在较少的试验次数下，对信号进行极小误差的重构[22]。定义运算符Ej(·)为EMD得到的第j个分量，CEEMDAN的实现步骤如下：

(1)

2)当j=1时，得到第一个残余量r1(t)：

(2)

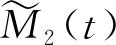
(3)

4)对于j=2,3,…,J，计算第j个残余量rj(t)：

rj(t)=rj-1(t)-Mj(t)

(4)

(5)

6)令j=j+1，返回到步骤4)，直到最后残余量不能再进行分解时方可终止分解：

(6)

即：信号X(t)经CEEMDAN分解成J个本征模态函数和一个残余分量：

(7)

2.2.2 小波阈值去噪原理

小波变换是傅里叶变换的发展与延拓，具有多分辨率的特点，广泛应用于信号处理领域[23]。假设一维信号为x(t)，满足平方可积，则小波基函数可表示为：

(8)

式中：t为时间；a为伸缩参数；τ为平移因子；ψ(t)为小波基函数；ψ*(t)是ψ(t)的共轭函数。

通过调整伸缩和平移因子的大小，选择合适的小波基函数及阶次对信号进行分解，再对每层高频系数阈值进行量化处理，最后由处理后的小波系数重构信号。

加载过程中出现的一段微震信号及振幅谱如图4所示。由图4可知，该信号振幅谱为单峰结构，频带较宽，能量主要集中在60 Hz左右。通过计算得到120～250 Hz频段信号幅值标准差为0.001 1，即该频段幅值大小相近，为高频噪声。

(a)含噪微震信号

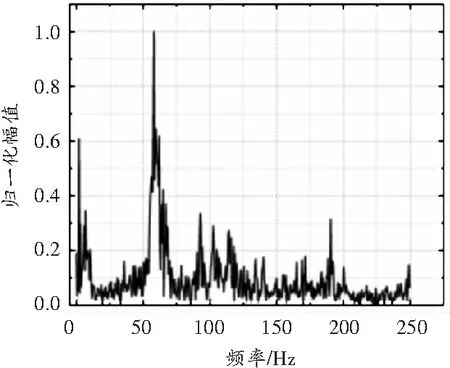
(b) 微震信号振幅谱

采用CEEMDAN法分解信号，在分解过程中，加入200组白噪声，标准差为0.2。信号经分解得到IMF1～IMF11共11个分量，其中前8个分量如图5所示。计算各分量的相关系数和方差贡献率，结合噪声呈现高频的特征及IMF6～IMF11的相关系数太小，最终选择IMF2、IMF3、IMF4和IMF5作为真实分量进行重构信号。

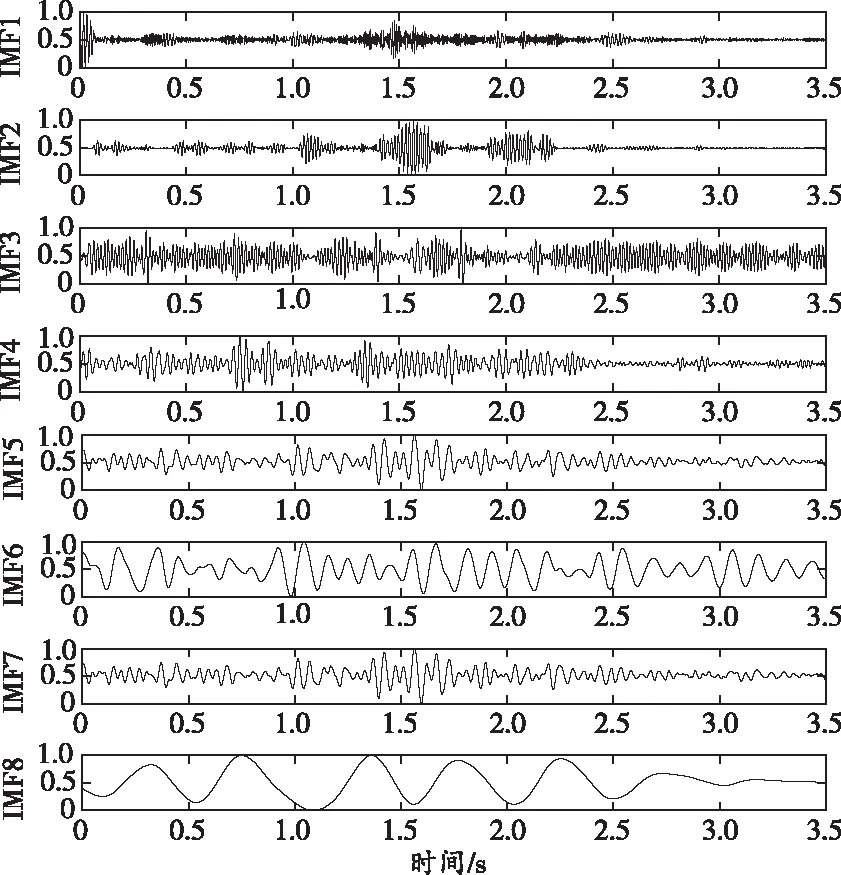
图5 CEEMDAN法分解得到的前8个分量

分别采用小波阈值和联合CEEMDAN—小波对微震信号进行降噪处理，小波阈值降噪中参数选择如下：sym8和db4小波基函数，无偏风险估计硬阈值(rigrsure)，分解阶次5阶。采用信噪比(SNR)和均方根误差(RMSE)2个指标来评估各算法的降噪性能，结果见表1。

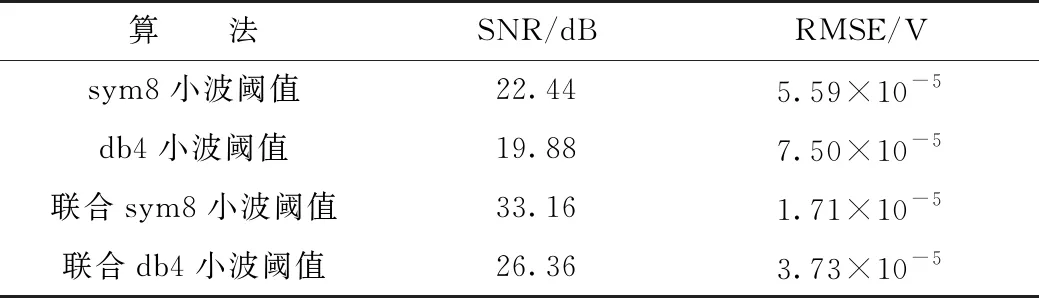
表1 各去噪算法效果对比

由表1可知，在选择sym8小波作为小波基函数的基础上，采用CEEMDAN—小波联合去噪的方法降噪效果最好，经该方法处理后的信号信噪比最大，均方根误差最小。联合去噪方法得到的重构波形及振幅谱如图6所示。

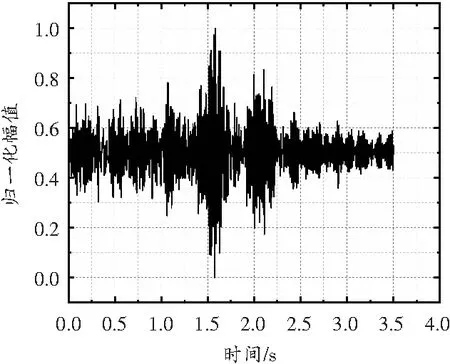
(a)联合去噪重构波形

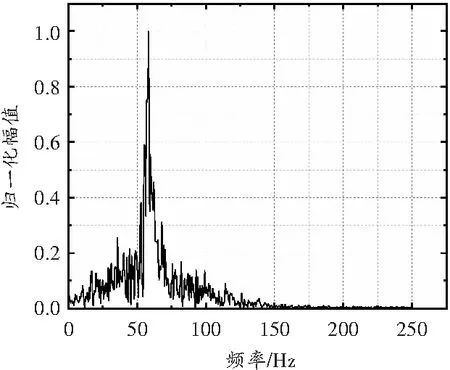
(b)联合去噪重构波形振幅谱

结合图6对比图4中的原始波形及振幅谱可知，联合降噪的方法不仅能减少信号的毛刺和不平滑现象，还能极大程度地保留低频信号，抑制高频噪声。

3 微震及声发射信号结果分析

3.1 微震时域波形参数分析

对微震监测系统采集到的全过程波形进行时域参数分析，可以看出各阶段微震信号幅值的变化情况。加载全过程的微震信号及过阈值曲线如图7所示。

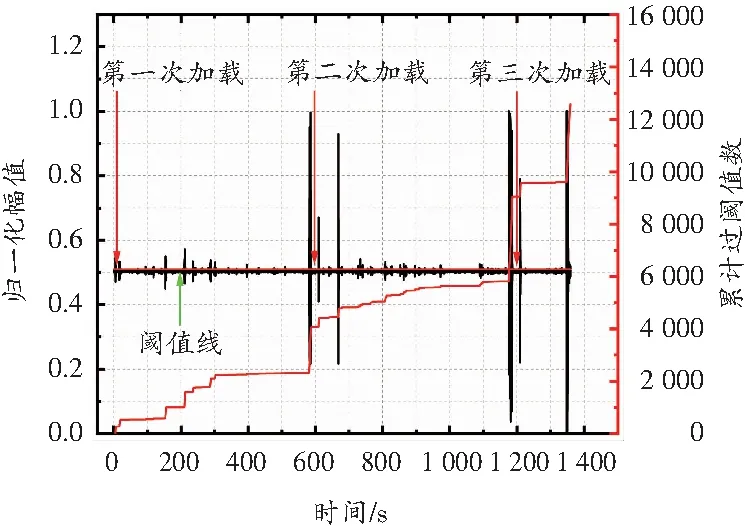
图7 全过程微震信号及累计过阈值数曲线

由图7可知，每次加载之后的数分钟内，都出现了幅值较大的突变信号，选取y=0.52作为阈值线，能更直观地看出各个阶段的幅值变化程度。随着加载的进行，幅值呈现阶梯状增加，在300～600 s时存在较为明显的平静期，证明加载前期并未出现较为明显的破裂，在接近破坏前，幅值达到最大值。

3.2 微震主频分析

由于时域分析不能反映微震信号的全部特点，因此引入快速傅里叶变换(FFT)对信号进行频域分析，采用2.2节信号去噪方法滤波后，以1 min为时间间隔划分时段，对每个时段的关键点波形做傅里叶变换处理,从而得到主频值，结果见图8。

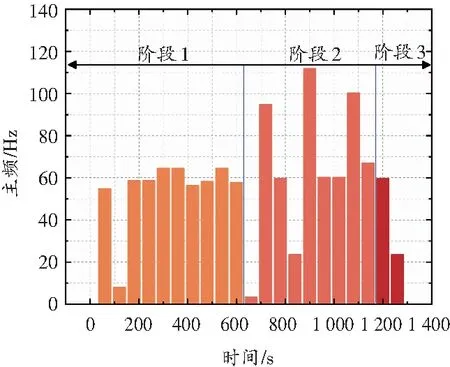
图8 主频随时间演化

由图8可知，每次加载时第1 min内的典型波形基本都呈现高频特征，加载至第2 min时，都出现了明显的低频信号，对应于图8中的120、660、1 260 s，每个加载阶段的过渡时间段主频变化并不明显。分析原因是每次加载过后，较短时间内都为内部的小裂纹扩展，所以呈现了高频特征，而到了中后期，一系列小裂纹聚合成大裂纹，出现了低频高能信号。

3.3 声发射信号及破裂机制分析

采用声发射技术对微震监测结果的可靠性进行验证。为保证参数分析的准确性，按照第2节的方法对波形进行白噪声判别，得到359个声发射信号。因声发射参数是依据门槛值来计算的，使得很多门槛值附近的微弱信号出现了上升时间和持续时间为0的情况，这样显然是不合理的。鉴于此，基于赤池信息准则[24](AIC)，编写程序提取波形的起始点，计算声发射参数。

图9为一段典型岩石破裂产生的声发射波形图，从中可以看出，AIC法能准确地捕捉到波形的起始点，保证了声发射参数计算的准确性。

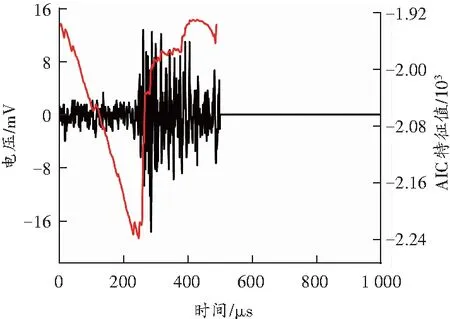
图9 AIC拾取声发射波形起始点

3.3.1 声发射时域参数分析

在声发射波形参数中，撞击计数和幅值能够直观地反映岩石内部破裂和强度变化情况。声发射荷载、幅值和累计计数随时间的分布情况见图10。

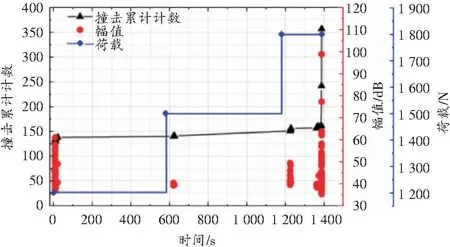
图10 声发射参数随时间分布情况

由图10可知，加载前期也能产生较多的信号，类似于单轴压缩试验中的压密阶段。分析原因是由预制裂纹过程中的损伤积累所致，随着加载的进行，岩石内部裂纹闭合，因此在中间阶段，几乎没有信号产生，类似于单轴压缩的弹性变形平静期阶段；随着进一步加载，内部小裂纹不断萌生和扩展，并伴随很多的应变能释放，故在临近破坏前几秒内，产生了大量的信号。

3.3.2 裂纹类型判据

国内外许多学者一致认为AF与RA的比值可用于判断裂纹是属于张拉型还是剪切型。日本JC MS-III B5706混凝土建筑规范[25]中，将分割线斜率(AF/RA)定义为k，将信号的AF/RA比值大于k的部分定义为张拉裂纹，反之为剪切裂纹，如图11所示。

图11 k值判断裂纹类型

OHNO K等[26]在研究混凝土弯曲试验中，发现将k=80作为分界线与矩张量分析结果较为相近。k的取值取决于材料的类型，笔者认为混凝土可被视为类岩石材料，两者的力学性质及破坏效应是极为相似的，所以本文亦将k=80作为判断裂纹类型的临界值。

3.3.3 RA-AF随时间分布

采用MATLAB编程计算微震和声发射各参数，研究RA-AF随时间的变化规律。按分级加载过程和声发射撞击几种分布时间，将信号按加载时间分段划分为t<10 s、10≤t<1 224 s、1 224≤t<1 373 s、t≥1 373 s共4个时段,4个时段RA与AF分布如图12所示。

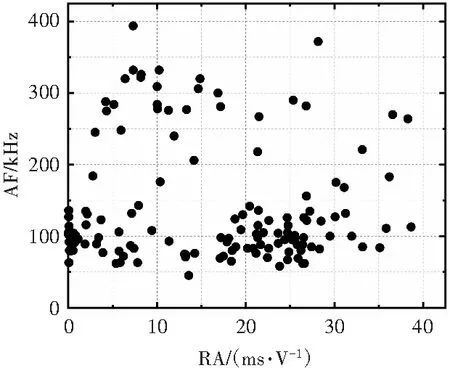
(a)t<10 s

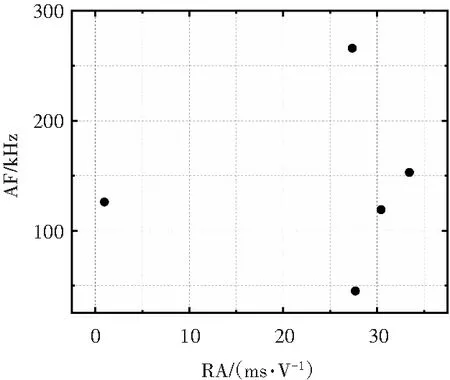
(b)10≤t<1 224 s

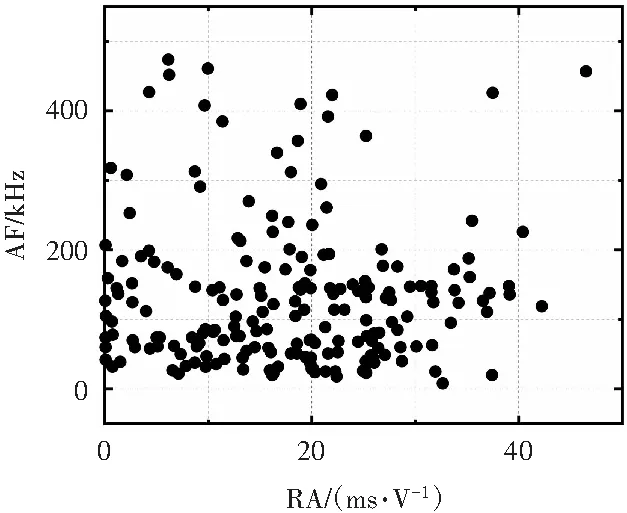
(d)t≥1 373 s

由图12可知，加载初期，信号的RA值与AF值都较大，RA主要集中在0～30 ms/V，AF集中在30～100 kHz，表示在此阶段张拉型微裂纹与剪切型微裂纹数量较为平均，两种破裂类型共同作用。随着加载的进行，信号产生较少，出现了一段相对平静期，证明在此阶段未出现显著破裂。临近破坏前1 min，信号开始增多，破坏前1 s内信号急剧增多，此时的信号对应较大的RA值(30～40 ms/V)，较小的AF值(50～80 kHz)，可见，此阶段相对于加载初期，张拉型破裂占比降低，剪切型破裂占比提高，以剪切型破裂为主导。

4 讨论

与传统的以变形监测为主的方法相比，声发射/微震监测方法具有显著的前兆信息和很高的灵敏度。采用应变片采集试验过程中的应变数据，结果如图13所示。

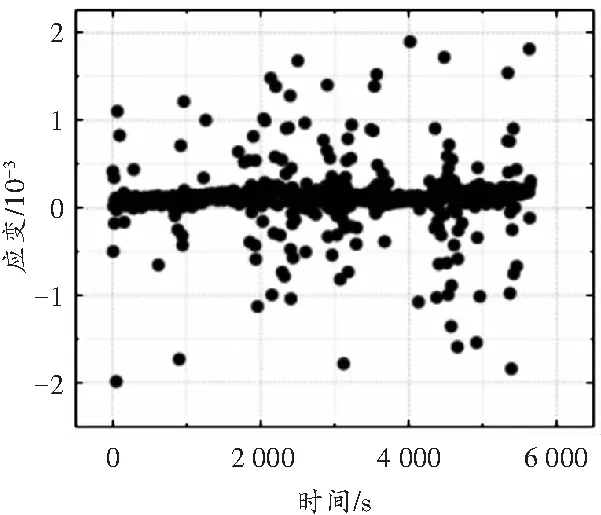
图13 应变随时间变化

由图13可知，应变值在很小的范围内波动，数据较为离散，且在低应力水平下的响应度很低，由于应变数据采集频率较低且破坏迅速，岩石破坏时的数据未能采集到，因此可认定为该尺度下是没有岩石破坏前兆信息的。但声发射和微震监测在这两方面表现都较好，根据图7和图10可知，微震和声发射信号与各个加载阶段对应性较好，破坏前的微震信号表现出低频特征，声发射信号剪切破裂占比出现突增。可见，相对于应变监测，声发射/微震监测对裂纹发展过程响应明显，在岩体崩塌监测预警方面具有较好的应用前景。