基于贝叶斯网络的煤矿顶板事故致因研究

秦 岩，盛 武

(安徽理工大学 经济与管理学院，安徽 淮南 232001)

顶板事故是煤矿安全生产中常见的事故之一,在我国,每年顶板事故发生的次数、造成的伤亡人数都居高不下，负面影响较大[1]。随着煤矿开采强度与深度的增加，煤矿顶板事故日益严重，给煤矿企业造成极大的经济损失和人员伤亡[2]。为了确保煤矿生产安全、降低顶板事故的发生率、维护煤矿工作人员的生命与财产安全[3]，基于顶板灾害事故的致灾因素，识别出煤矿顶板事故的关键影响因素，对避免顶板事故的发生具有重要的意义。

事故致因分析(Accident-Causing Theory)是从大量事故案例中提取信息，进行变量分析及事故形成原因的判定与诊断，探究事件发生的规律，能够为事故的预防与安全管理工作的改进从理论上提供科学详实的依据[4]。致因分析研究的常用方法有博弈论—TOPSIS法、层级分析法(AHP)、灰色系统理论、解释结构模型(SIM)、神经网络分析法等，杨君岐等[5]利用BP神经网络对商业银行风险进行了评估研究；王慧雯等[6]结合N-K模型和TOPSIS模型构建了煤矿顶板风险因素的评价模型；薛海腾等[7]运用改进AHP方法对煤矿瓦斯爆炸事故关键因素进行了分析。贝叶斯网络(Bayesian network,简称BN)模型是一种基于贝叶斯因果概率推理的概率网络模型[8]，该模型先利用先验数据构建初始模型，再通过参数学习对初始模型进行改进。目前，已有部分学者利用贝叶斯网络对煤矿事故进行分析研究，如陈兆波等[9]将HFACS与贝叶斯网络相结合构建了网络模型，对事故发生的深层次人为因素进行了推理研究，进一步提高了事故原因调查的可靠性；李世科[10]采用K-均值聚类与贝叶斯判别法对顶板灾害进行了评价，得出了更为准确的评价结果，同时还分析了方法的优越性;李贤功等[11]利用K2算法构建了顶板事故贝叶斯网络模型，分析了影响事故的因素。虽已有学者基于人、物、环、管4个方面对煤矿顶板事故进行了致因分析，但系统深入研究的文献较少。基于此，笔者在前人相关研究的基础上，结合煤矿顶板事故调查报告，从人为、设备、环境、管理4个方面选取事故致因变量，采用贝叶斯网络进行结构和参数学习，以及敏感性分析等，通过最大致因链找出关键因素，以期为精准识别顶板事故影响因素提供参考。

1 数据来源和变量选取

以2010—2020年为研究时段，收集整理国家煤矿安全监察局官网中的煤矿事故调查报告作为数据来源，共获取64起煤矿顶板事故案列分析调查报告。采用数据驱动思想，从人为、设备、环境、管理4个方面考虑变量。为满足建模需求，将属性变量转换为虚拟变量，并对变量中的连续变量进行离散化，各变量的设置如表1所示。

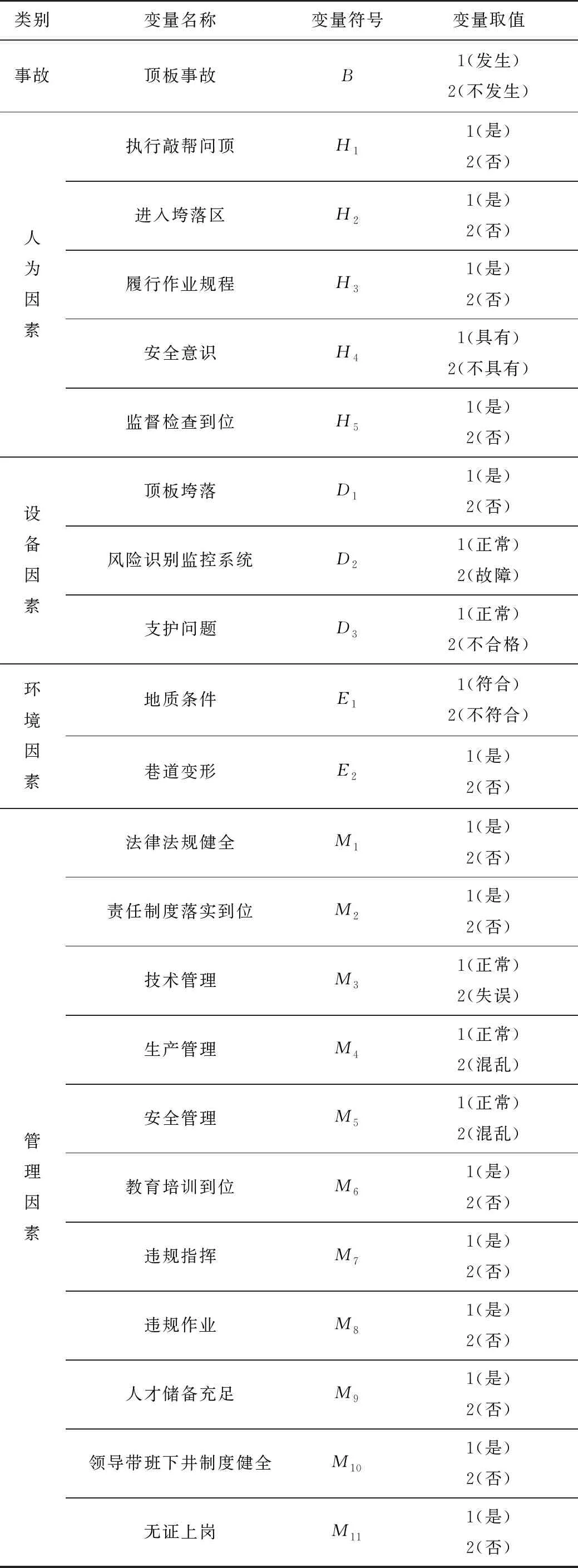
表1 煤矿顶板事故致因变量设置

2 贝叶斯网络原理

贝叶斯网络也被称为信念网络(Belief Network)，是基于多元统计分析技术的贝叶斯决策方法的一种统计推理方法，于1988年由Pearl[12]提出。贝叶斯网络是基于贝叶斯概率推理与图论的结合，也是主要解决不定性或不完全性的信息决策。同神经网络类似，其也是由节点圆圈、有向边组成的1个有向无环图(DAG)，通过节点之间传播新的信息，其中节点圆圈和有向边分别代表变量和变量之间的因果关系。贝叶斯网络如图1所示。

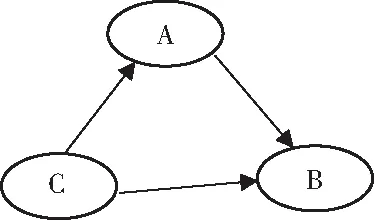
图1 贝叶斯网络

设事件样本A中，影响其发生的n个事件(A1,A2,…,An)。相关的贝叶斯表达式如式(1)所示：

(1)

式中：P(Ai)为事件的先验概率；P(B|Ai)为事件Ai发生条件下事件B发生的概率；P(Ai|B)为后验概率；i=1，2，…，n。

其节点的联合概率分布P(A)为：

(2)

式中：A为网络中的各个节点变量；Pa(Ai)为节点Ai的所有父节点。

3 变量相关性分析

为提高贝叶斯网络模型预测的精确度，通过降低数据维度、简化模型结构，利用SPSS 24.0软件对变量进行Pearson相关性分析，其计算公式如下：

(3)

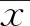
选出相关性较强的变量，筛选结果如表2所示。

由表2可知，不同节点之间相关程度不同，具有显著相关的节点较多，说明节点之间关系相关性较强。其中节点M5(安全管理)和B(顶板事故)的相关性最强，在0.01水平上达到0.568且呈负相关关系，说明节点M5(安全管理)相关程度越高，B(顶板事故)发生的概率越小；其次，M8(违规作业)和M7(违规指挥)相关程度在0.01水平上达到0.517且呈正相关关系，说明M8(违规作业)相关程度会随着M7(违规指挥)相关程度的变化而变化。

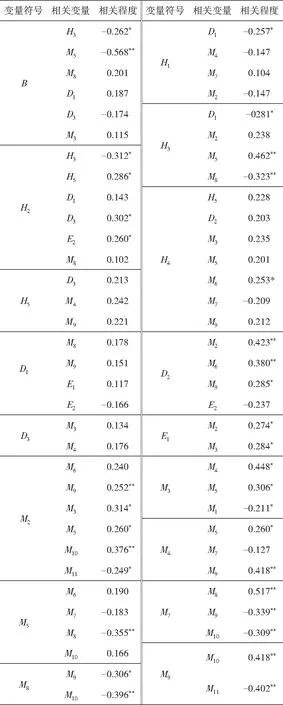
表2 节点变量相关性

4 贝叶斯网络模型构建

将处理后的结构化数据导入贝叶斯网络软件GeNie中，借助相关算法进行结构学习。在此基础上，结合节点相关性分析结果对贝叶斯网络模型进行调整与修正，最终构建的煤矿顶板事故致因贝叶斯网络模型如图2所示。

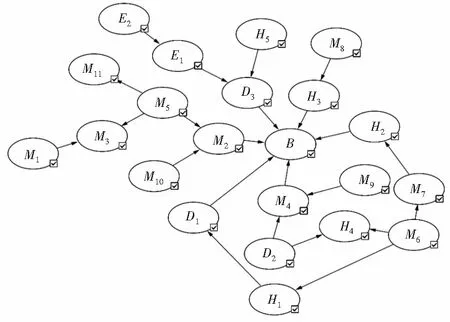
图2 煤矿顶板事故致因贝叶斯网络模型

由图2可以看出，贝叶斯网络模型从整体上反映了煤矿顶板事故的发生原因及各原因之间的因果关系，各节点间的连线箭头由因指向果且表明两变量之间的关系。节点B(顶板事故)是模型中的研究对象，与D1(顶板垮落)、D3(支护问题)、H2(进入垮落区)、M2(责任制度落实到位)、H3(履行作业规程)和M4(生产管理)均存在明显的内在因果逻辑关系。除此之外，其他节点与节点之间也存在密切的因果关系，研究其关系能够深入挖掘煤矿顶板事故发生的诱因，从源头找到最重要的影响因素。

5 贝叶斯网络模型验证与推理

5.1 模型验证

为了验证贝叶斯网络模型的可靠性和预测性，对网络模型进行有效交叉验证[13]。采用Leave One Out Cross验证方法对模型各节点的预测精准度进行有效性计算，验证结果如表3所示。由表3可以看出，在22个节点中，目标节点“顶板事故(B)”的预测精准度达到最高，为0.984；其次是节点“安全管理(M5)”的预测精准度，为0.953。从整体来看，大多数节点的预测精准度在0.7以上。这说明本文构建的贝叶斯网络模型具有较高的预测精准度，适宜对煤矿顶板事故的致因关系进行推理与分析。

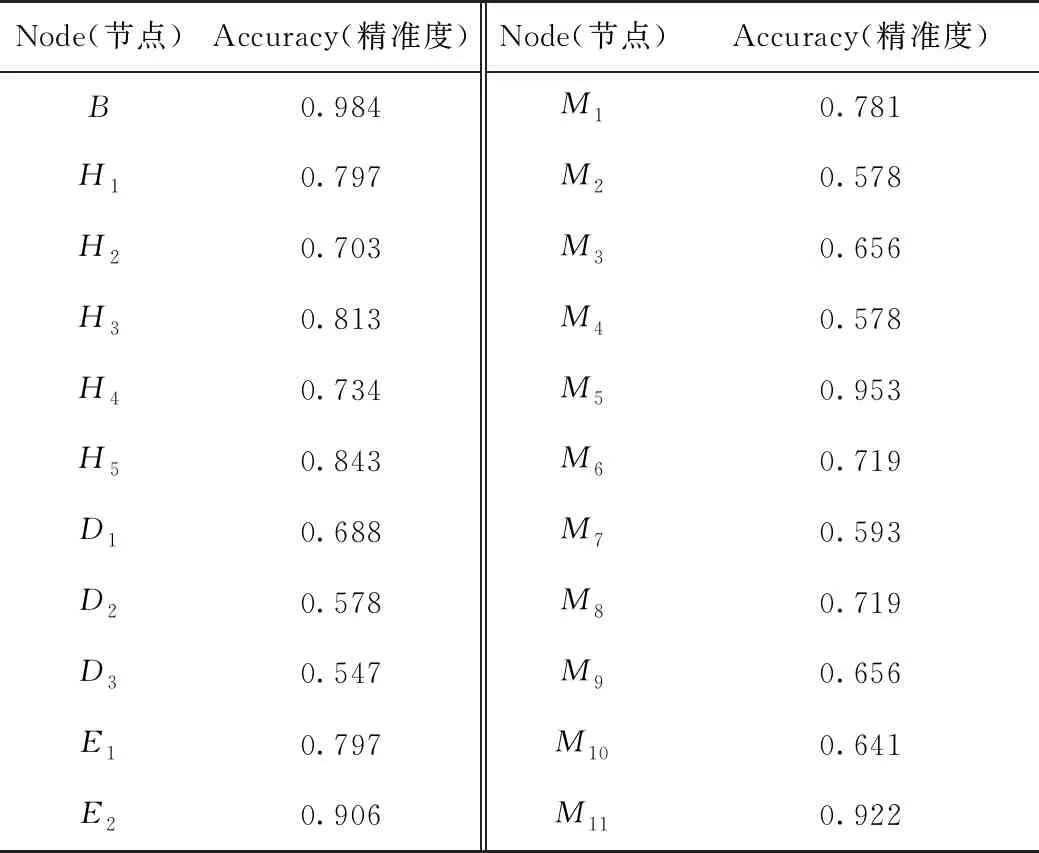
表3 模型交叉验证结果

5.2 参数学习

贝叶斯网络的参数学习是为了确定节点变量的条件概率分布情况，对模型节点变量间的依赖关系程度进行量化[14-16]。目前，主要的参数学习算法包括贝叶斯方法、期望最大化算法(EM)和最大似然估计算法(MLE)[17]等。在此，笔者选用期望最大化算法，主要因为期望最大化算法可在数据缺失的情况下对参数进行极大似然估计，能更好地应用于各类不完整数据的处理。其分为期望计算E-步和最大化计算M-步2个步骤[18]，具体算法见式(4)、式(5)。

1)E-步(Expectation-Step)：根据观测到的数据和当前的参数值，计算样本数据的对数似然期望公式为：

Q(Θ，Θ(t))=E[logP(X|Θ)|Θ(t),M]

(4)

式中：Θ为当前数据参数值；Θ(t)为上一迭代得到的参数估计值；E(x)为取变量x的数学期望；logP(X|Θ)为观测数据中事件发生的条件概率；X为要研究的事件；M为样本数据集。

2)M-步(Maximization-Step)：对E-步的发生概率期望进行最大化期望值计算Q(Θ，Θ(t))，即：

(5)

将E-步和M-步反复迭代，从而获取最优解。

在贝叶斯网络中，贝叶斯条件概率表是反映节点间关系的纽带，是进行贝叶斯网络推理的基础[19]。通过贝叶斯网络的参数学习可得出各节点间的条件概率，因节点数量较多且篇幅所限，仅着重分析关键词节点D3(支护问题)、M4(生产管理)和M3(技术管理)的条件概率分布。为此，将设置好的节点名称与状态进行数据匹配，其中“normal”表示节点状态取值为“正常”；“abnormal”表示节点状态取值为“不正常”；“yes”表示节点状态取值为“是”；“no”表示节点状态取值为“否”；“conformity”表示节点状态取值为“符合”。有关节点条件概率如表4～6所示。

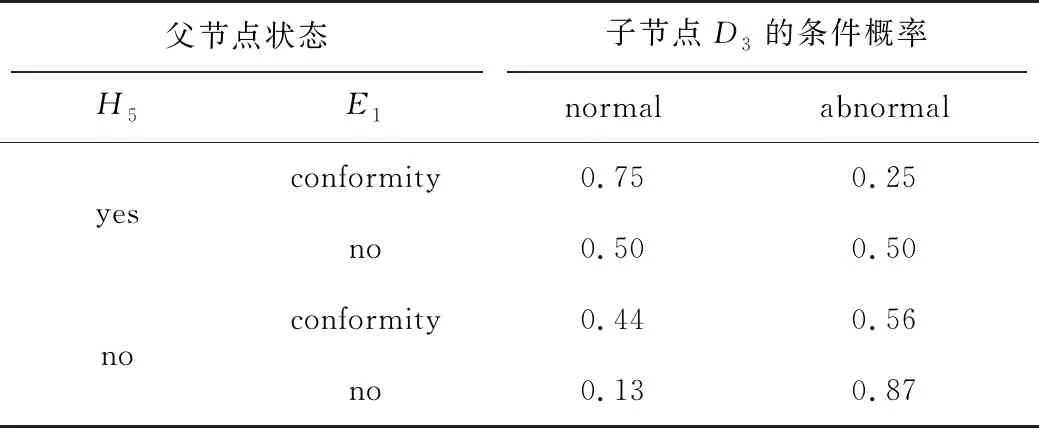
表4 节点D3的条件概率

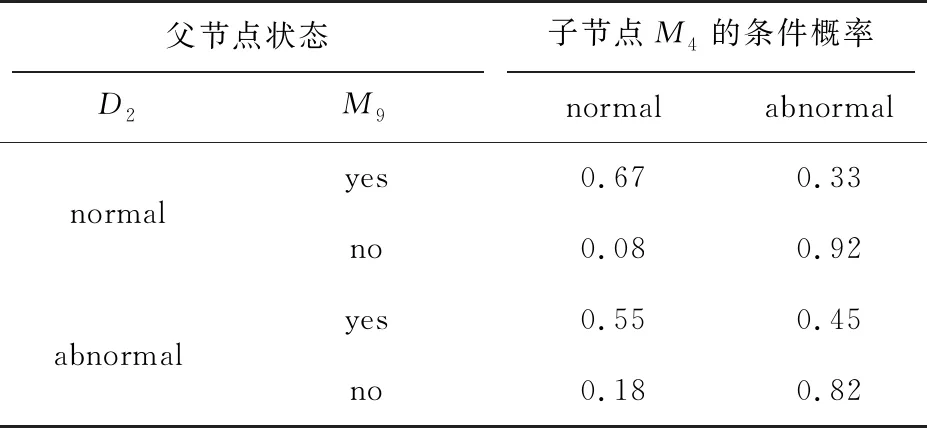
表5 节点M4的条件概率

表6 节点M3的条件概率

由表4可知，当人员监督检查不到位(H5取值为no)、环境地质条件不符合安全生产要求(E1取值为no)时，支护发生问题(D3取值为abnormal)概率最大，概率值为0.87。因此，在煤矿发生顶板事故的过程中，以上两种情况若同时发生，则有很大概率会导致顶板事故的发生。相反，当人员监督检查到位(H5取值为yes)、地质条件也符合要求(E1取值为conormity)时，支护不正常问题(D3取值为abnormal)的发生概率为0.25，煤矿顶板事故发生的概率则变小。同时，当人员监督检查到位(H5取值为yes)、而地质条件不符合要求(E1取值为no)时，与E1取值为conformity相比，支护问题不正常的概率增大了1倍。对比发现，地质条件不符合安全生产要求将会提高顶板事故发生的概率。

由表5可知，当风险识别监控系统正常(D2取值为normal)，人才储备不充足时(M9取值为no)，生产管理混乱(M4取值为abnormal)的概率值为0.92，这说明在煤矿生产过程中，要注重培养人才、提高员工管理能力或引进人才。

由表6可知，在法律法规健全(M1取值为yes)，安全管理处于正常状态(M5取值为normal)时，技术管理处于正常状态(M3取值为normal)的概率为0.88；反之，当法律法规不健全(M1取值为no)、安全管理处于混乱状态(M5取值为abnormal)时，技术管理则处于混乱状态(M3取值为abnormal)，概率高达0.93。这充分说明在开展顶板管理工作的过程中，应同时完善法律法规和安全管理规章制度，通过提高管理能力来预防顶板事故的发生。

5.3 贝叶斯网络模型节点逆向推理

贝叶斯网络模型节点逆向推理是在已知网络模型目标节点的情况下，计算其他节点变量的后验概率[20]。笔者构建了贝叶斯网络模型，对变量进行逆向推理，得出其他节点变量的后验概率值,更能准确地对事故态势进行评估与预测。在构建的贝叶斯网络模型基础上，将根节点“顶板事故(B)”设为证据节点，得出其他节点的后验概率分布。分析比较各节点后验概率值的大小，推断导致煤矿顶板事故发生的最可能原因，结果如表7和图3所示。

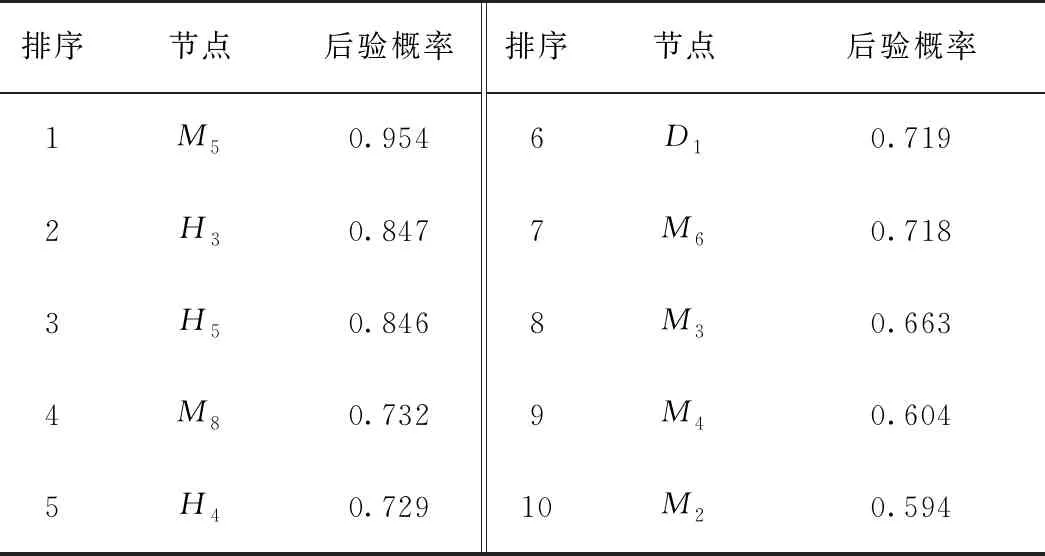
表7 煤矿顶板事故后验概率前10节点变量排名

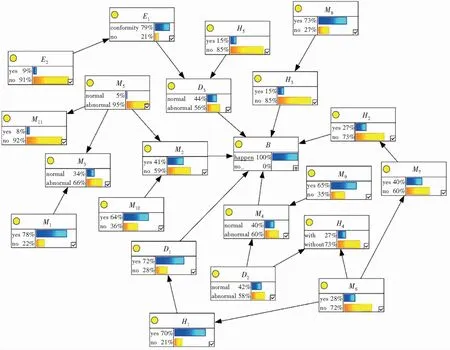
图3 贝叶斯网络模型节点逆向推理分布图

由表7和图3可知，在煤矿顶板事故已发生的情况下，煤矿企业各级安全管理混乱(M5取值为abnormal)，概率大于95%；其次为未履行作业规程(H3取值为no)，概率大于84%；节点监督检查不到位(H5取值为no)，概率大于84%；节点违规作业(M8取值为no)，概率大于73%；员工缺乏安全意识(H4取值为no)，概率接近73%；节点发生顶板垮落(D1取值为yes)和教育培训不到位(M6取值为no)，概率大于71%；技术管理失误(M3取值为abnormal)，概率大于66%；节点生产管理运行混乱(M4取值为abnormal)，概率大于60%；煤企责任制度落实不到位(M2取值为no)，概率大于59%。

5.4 节点敏感性分析和最大致因链分析

在贝叶斯网络模型中，对敏感性分析能够反映网络模型由局部参数发生变化而引起对目标节点的量化[21]，进而识别出模型中的敏感性因素，节点红颜色的深度与其敏感度呈正比关系，红色越深，则敏感性程度越高；同时，通过事故最大致因链寻找关键性风险因素，用箭头加粗风险致因链即最可能导致事故发生的关键风险路径。将节点B设定为目标节点，进行变量敏感性和事故最大致因链分析，结果如图4所示。

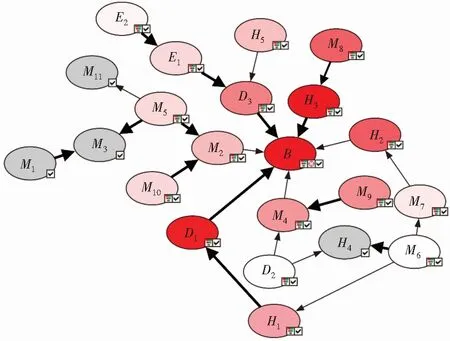
图4 贝叶斯网络模型节点变量敏感性和最大致因链分析

由图4可以看出，网络模型节点的敏感性程度不同，敏感性较高的节点有：H3(履行作业规程)、D1(顶板垮落)、H2(进入垮落区)、M8(违规作业)、D3(支护问题)、M4(生产管理)、H1(执行敲帮问顶)、M9(人才储备充足)，对这些因素进行重点防控，能够有效提高抵抗事故发生的能力。图4中造成煤矿顶板事故的致因链中，最长致因链为E2(巷道变形)→E1(地质条件)→D3(支护问题)→B(顶板事故)；其次为H1(执行敲帮问顶)→D1(顶板垮落)→B(顶板事故),M8(违规作业)→H3(履行作业规程)→B(顶板事故)。因此，应针对以上关键风险因素优先加以控制，降低最大致因链中各因素的发生概率。煤矿井下作业时应全面掌握矿区地质构造发育情况，严格履行安全生产和作业规章制度，及时对设备进行检修排除隐患，提高全员的煤矿安全防范意识，保障人员与财产安全，有效预防顶板事故的发生。

6 结论

1)经过整理和调查煤矿顶板事故的相关资料，采用数据驱动研究模式，从人为、设备、环境、管理4个方面选取致因变量，分析因素间相关关系，并交叉验证了贝叶斯网络模型的可靠性与精准度。

2)利用贝叶斯网络软件GeNie 构建事故模型，采用EM算法对贝叶斯分析模型进行参数训练，了解变量间的概率分布情况；运用逆向推理、敏感性和最大致因链分析，得出对顶板事故影响显著的致灾因素。

3)节点H3(履行作业规程)、D1(顶板垮落)、H2(进入垮落区)、M8(违规作业)的敏感性较强；其次，分析得到E2(巷道变形)→E1(地质条件)→D3(支护问题)→B(顶板事故)最长致因路径。根据致灾因素分析结果进行预防，是降低煤矿顶板事故发生的关键手段和有效方法。