双液滴撞击液膜的界面追踪法数值模拟

胡中全，李竞伦，徐猛，马自强，李培生

(1.南昌大学先进制造学院，江西 南昌 330031；2.西安交通大学能源与动力工程学院，陕西 西安 710049)

液滴撞击液膜的现象广泛存在于自然界和工业生产中，如3D打印技术、油-汽润滑系统[1-2]、喷雾燃烧、DNA微阵列和轴对称流聚集技术[3]等。迄今为止，国内外学者主要研究方向都集中在实心液滴或中空液滴撞击固体壁面或液膜。其中，陈烽等[4]对液滴撞击固体表面过程进行了实验研究，探究了液滴的物性和操作条件对撞击过程的影响，结果表明，铺展直径、面积和表面能随时间变化先增大后减小，而动能为先减小后增大。Yokoi[5]采用了CLSVOF(coupled level set and volume of fluid)方法研究水滴撞击水平固体壁面的飞溅现象，研究发现，壁面的接触角越大，液滴越容易飞溅。Vander Wal等[6]分析了不同液滴撞击固体壁面以及同种液滴撞击不同液膜，并定性分析了液膜黏度、表面张力以及撞击速度对撞击形态的影响，结果表明，撞击速度、液膜黏度和表面张力越小，其形态变化越剧烈。杨亚晶等[7]探究了液滴撞击液膜后相互作用的过程、穿越模式以及运动特性，并总结出随着韦伯数的增大，液滴与液膜之间出现的5种不同的穿越模式。裴毅强等[8]对单液滴撞击不同黏度液膜特性进行了研究，拟合出冠状形态的临界韦伯数与无量纲液膜厚度的关系式，以及无量纲冠顶高度和冠顶直径与入射液滴韦伯数的关系式。张莹等[9]对液滴撞击液膜动力学特性进行数值模拟，模拟显示在水平方向上，在撞击影响不到的区域里不存在压力的变化，而在射流形成处的颈部附近存在局部的压力差；液滴撞击液膜是其间的气体被压缩，在流体黏性和剪切力的作用下，压力高的气层中可产生卷吸现象。闫哲等[10]对中空液滴撞击液膜进行了数值研究，分析了不同液膜厚度、液壳厚度以及撞击速度对传热特性的影响，发现了平均热流密度的变化特性。Brasz等[11]对上升气泡破裂后产生射流的过程进行了模拟，得到了黏度、上升速度和气泡大小对射流尺寸的影响。林圣享等[12]探究了双液滴在下落过程中的不对称性和互相排斥性，得出在增大Re和Eo时，此类现象会更加明显的结论。

通过上述文献可知，在如今众多的多相流问题的研究中，国内外学者对液滴撞击壁面或液滴撞击液膜的此类问题使用的模拟方法多以格子-玻尔兹曼(LBM)方法[13-14]和液体体积法(VOF)为主，其中LBM方法能够有效地处理方腔对流换热问题，但处理相界面时存在精度不高和计算资源量较大的问题；而VOF方法很难计算出界面的曲率，界面重构复杂，易产生数值性破碎。而界面追踪法(FTM)以其对物理方程的独特理解，对运动界面进行重构，能够精准地捕捉运动界面而不发生非物理现象，相比于其他数值模拟方法，FTM是多相界面捕捉算法中精度最高的一种，在捕捉气液两相流、凝固及火焰传播等运动界面方面有明显的优势[15-17]。其中Ma等[18-20]使用FTM对气泡流系统进行了精确的数值模拟，Lin等[21]也使用界面追踪法对气泡振荡流动问题进行了更为深入的研究。本文基于FTM模拟了在不同韦伯数、无量纲液滴间距和无量纲液膜厚度下对双液滴撞击液膜时的形态演变、射流中心高度和卷吸气泡产生的影响，分析了在韦伯数数值较高的条件下射流中心发生断裂形成二次液滴的机理，这将为喷雾燃烧、细胞打印等领域提供一定指导意义。

1 物理模型与数值方法

1.1 气液两相流的Navier-Stokes方程

二维不可压缩流动的动量方程为

(1)

式中：ρ表示密度；u表示速度矢量；p表示压强；g表示重力加速度；μ表示黏度；σ表示表面张力系数；κ表示平均曲率；δ表示狄拉克函数；n表示界面处的法向量；xf表示界面位置。

1.2 界面追踪法(FTM)

在求解Navier-Stokes方程时，使用了二阶投影法[18-19]：

(2)

通过求取方程两边的散度，得到了压力泊松方程：

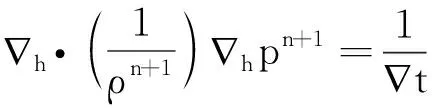
(3)

式(3)中下标h表示空间上的离散量，而上标n+1表示的是时间上的离散量，速度u*的定义如下：

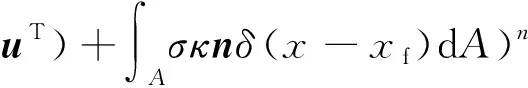
(4)

如图1所示，在界面追踪方法中，采用静态欧拉网格来求解流体流动过程物理参数，同时通过单独的拉格朗日网格明确地追踪界面，界面通过有序的点标记。

完成界面的标记之后，FTM界面标记点上的信息是通过网格上的信息来获取得，这个过程一般使用面积加权函数来实现，如图2所示，对固定网格上的信息进行二维线性插值就可以得到网格内界面标记点的信息，表达通式为：

(5)

在界面移动的过程中，为了确定气液多项流时时变化的密度和黏度，需要采用密度跳跃的方法，并引入Heaviside函数：

(6)

式中：φ为给定点到界面的位置；2α为两种流体之间过渡区域厚度绝对值。

5#支管设计流量时，5#与4#支管同时或依次关闭，最大压力88.4 m，发生在桩号23+294处。5#支管流量最小时，5#支管与4#支管300 s同时或依次关闭，最大压力108.4 m，发生在桩号23+294处。

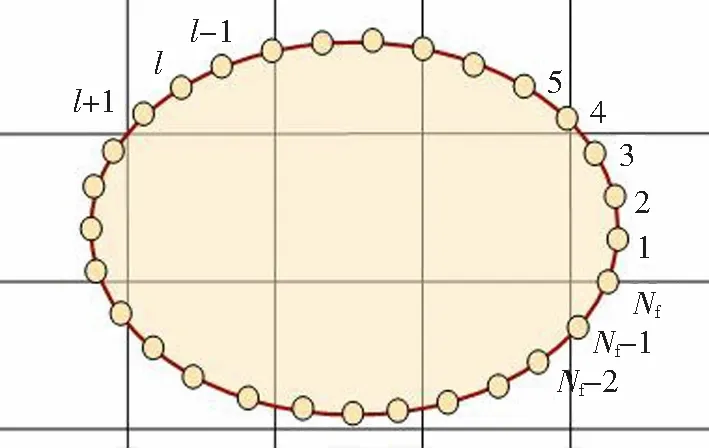
图1 FTM界面标记示意图Fig.1 FTM interface marking diagram

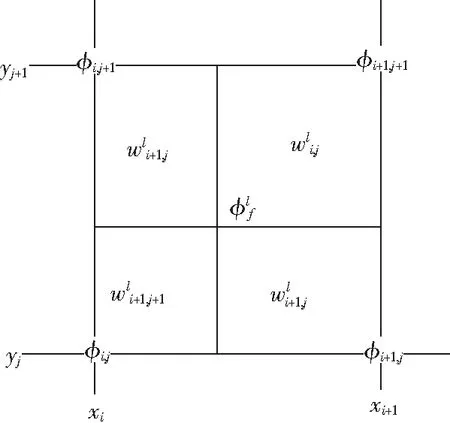
图2 面积权重函数示意图Fig.2 Schematic diagram of area weight function

1.3 表面张力

在模拟不相溶的多相流时，求解表面张力对精准追踪界面十分重要，所以使用的表面张力计算方程如下：

Fσ=σκnδ(x-xf)

(7)

式中：Fσ为表面张力。

取单位元上的表面张力为研究对象，则对于二维流动有：

(8)

对式(8)进行积分，可得到单位界面元的总表面张力：

(9)

式中：τ表示为界面上的切向量；s为界面元；l为界面上的节点。

1.4 物理模型

在对两液滴同时撞击液膜进行数据模拟时，计算域物理模型如图3所示，模型计算域尺寸设置为10D×5D，在此计算域中两直径为D的液滴以U的竖直速度同时撞击厚度为H的液膜。其中环境介质为空气，液膜与两液滴为相同液体。初始时刻，两液滴位于液膜上方，只考虑重力，其他质量力均不考虑。

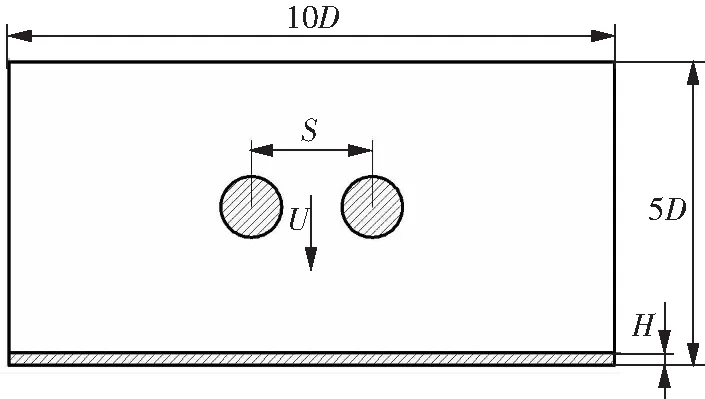
图3 物理模型Fig.3 Physical model

1.5 模型验证

多相流动中存在复杂的流动过程，使得数值模拟结果与试验结果保持一致显得极为关键。为了验证FTM数值模拟方法的准确性，取用与文献[9]中相同的物理参数，不同时刻的界面形态如图4所示，红蓝彩图为模拟结果，黑白线图为文献中的结果。可以看出，在液滴撞击液膜后，液滴直接融入液膜，并未激起水花，也没有液滴颈部毛细波的形成。模拟得到的液滴形态变化规律与文献中的结果一致，证明了该方法的适用性与准确性。

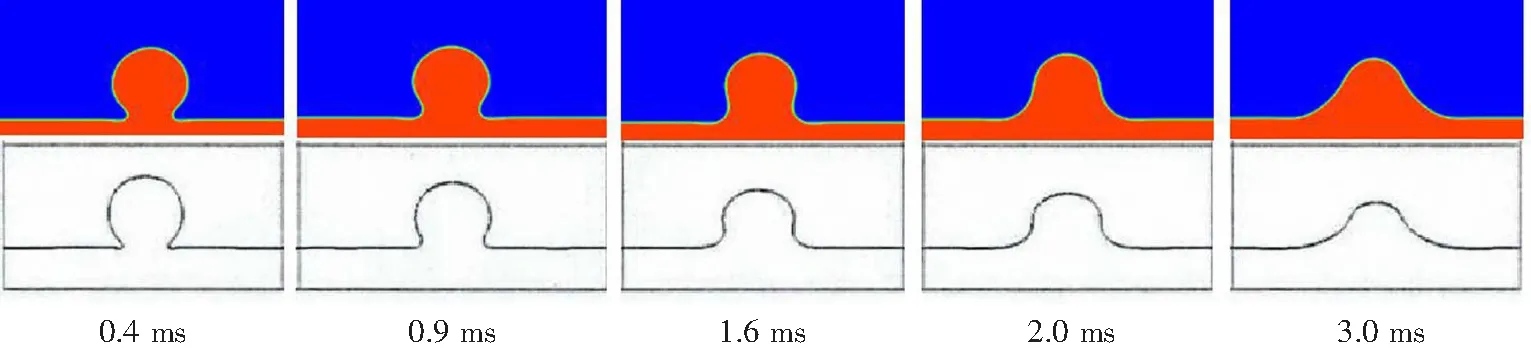
图4 FTM模拟与文献[9]中的结果对比图Fig.4 Comparison of FTM simulation with results in literature[9]

1.6 网格无关性验证

网格无关性验证结果如图5所示，当U=1.0 m·s-1，δ=0.2,无量纲时间为0.09时，在交错网格中，分别对在网格精度为260×130，520×260和840×420下生成的形态演变界面进行对比，结果发现网格精度为520×260时图像最为理想。因此本文会在520×260的网格精度下进行数值模拟。

2 数值结果与讨论

2.1 双液滴撞击液膜模拟

图6给出了We=271、δ=0.2时，双液滴撞击液膜的界面演化图。可以看出无量纲时间τ=0.002时，两个平行液滴同时开始接触并融入液膜；然后当τ=0.038时，液滴与液膜撞击融合过程中形成了较低的水花，同时液滴继续融入液膜，推动水花向外侧发展；接着τ=0.052，向中心发展的水花相遇，并且水花的底部开始融合，中心射流开始形成；τ=0.058时，向中心发展的水花已完全融合，中心射流形成，液滴基本融入液膜；最后τ=0.088时，液滴已完全融入液膜，中心射流在动能的驱动下继续向上发展，向两侧发展的水花形成完整的冠状水花。

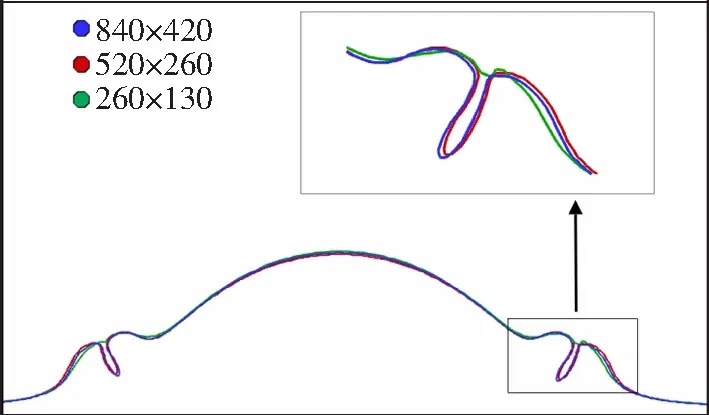
图5 网格无关性验证Fig.5 Grid independence verification

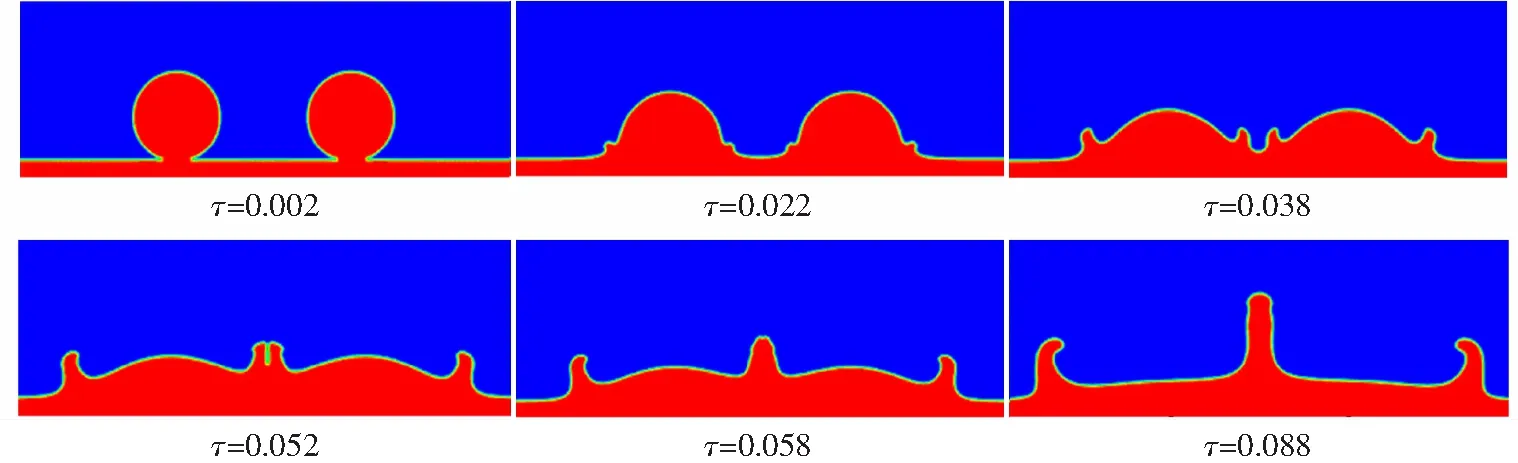
图6 We=271时双液滴撞击液膜的界面形态演化图Fig.6 The interface evolution diagram of double droplets impacting on the liquid film at We=271

2.2 中心射流的影响因素

图7给出了不同We数下中心射流的界面形态演化图。可以看到，液滴与液膜撞击融合过程中，向中心发展的水花相遇融合，中心射流开始形成。图中每一列图片对应的无量纲时间分别是τ=0.058、τ=0.078、τ=0.108、τ=0.182。可以看出，不同韦伯数下的中心射流界面形态有着显著差别。但其变化过程有一定的规律可循，那就是中心射流形成后，不断向上运动，随着射流的速度减慢，液体不断向上聚积，形成一个顶部大中部细的射流形状。还可以看出，当We=120时，气体被吸入液膜中形成巻吸气泡，这些气泡随着液体的运动进入中心射流。当We=482时，中心射流的形状更像一种伞形结构，其顶部液滴存在向两侧发展的趋势，最终破碎形成二次液滴。

图8为不同We数下无量纲中心射流高度随无量纲时间的变化曲线图。中心射流一开始以很快的速度发展，然后慢慢达到最高点，接着开始回落。可以得到，We数越大时，中心射流出现的时间越早，并且中心射流能够达到更高的极限高度。说明更大的We数能够促进中心射流的产生与发展。图9给出了We=271时，不同无量纲液滴间距下无量纲中心射流高度随时间的变化曲线。可以看出，随着无量纲间距的增大，中心射流出现得越晚，并且中心射流所能达到的最大高度也越低。两液滴间距越大，单一液滴撞击液膜所产生的水花运动至碰撞相融的时间也就越久，因此出现中心射流的时刻就越晚，单个液滴撞击时的动能大多转化为撞击水花形成与发展所需要的能量，并且动能在向内发展的过程中也在被消耗，中心射流的形成必然受到影响，因此，液滴间距越大，水花融合后形成的中心射流能够达到的最大高度就越低。

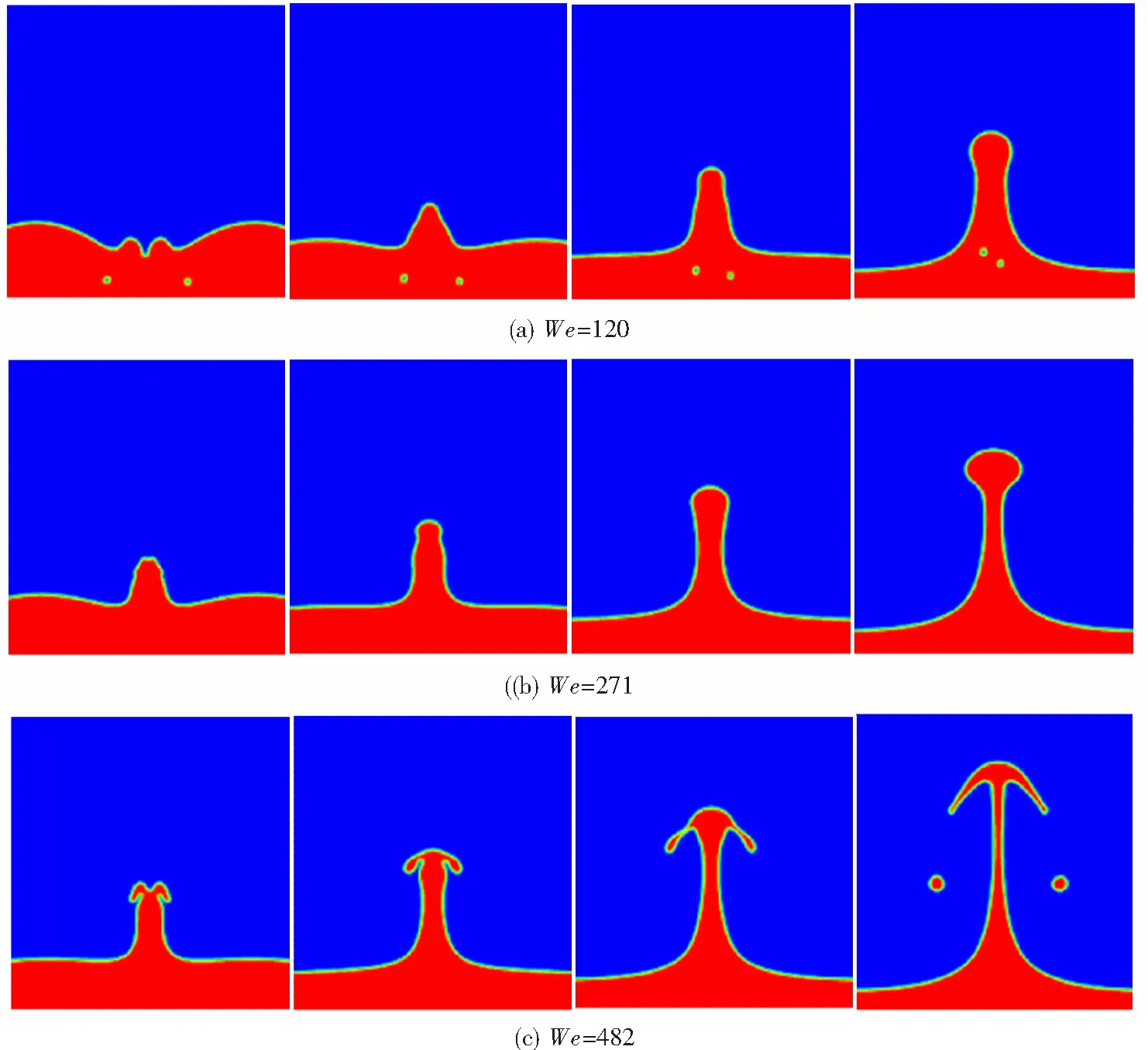
图7 不同We数下中心射流界面形态演化图Fig.7 Interface evolution diagram of the central jet under different We

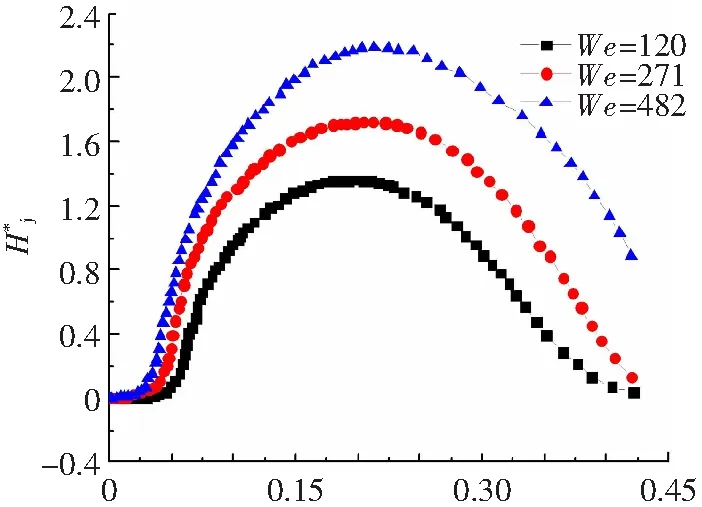
τ图8 不同We数下无量纲中心射流高度随无量纲时间的变化曲线Fig.8 Variation of the dimensionless height of the central jet with dimensionless time at different We

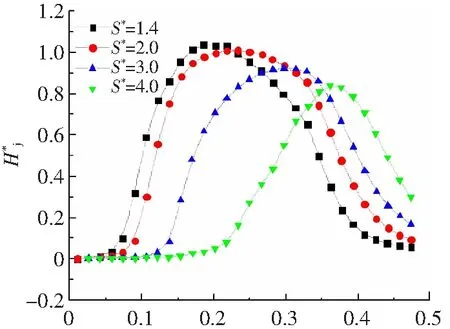
τ图9 不同无量纲液滴间距下无量纲中心射流高度随无量纲时间的变化曲线Fig.9 Variation of the dimensionless height of the central jet with dimensionless time at different dimensionless droplet spacing

2.3 卷吸气泡的形成和影响因素

本文对双液滴在不同We数下同时撞击水平液膜的过程进行了大量的模拟，最终发现，当We数在30～276这个范围内，才会出现液膜卷吸空气形成气泡的现象。图10绘制了不同液滴间距下气泡成型时间随We数增大的变化曲线，可以得到随着We数的增大，液膜卷吸空气形成气泡的时间逐渐缩短，说明更大的We数能够加快气泡的形成。图11给出了无量纲气泡尺寸随We数的变化曲线，可以看出，We数越大，生成的气泡尺寸就越大。这是由于流体的运动随着We的变大而加快，这样就能更快地封闭弧形气室，将更多的气体保留在液膜内，气泡的尺寸就越大。

We图10 气泡成型时间随We数的变化曲线Fig.10 Variation of bubble forming time with We

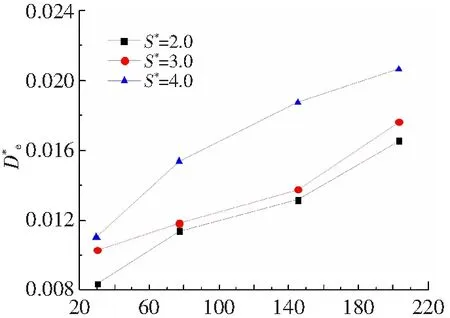
We图11 无量纲气泡尺寸随We数的变化曲线Fig.11 Variation of dimensionless bubble size with We

图12探究无量纲液滴间距对液膜卷吸空气形成气泡的影响，可以看出随着无量纲液滴间距的增大，卷吸气泡成形时间在减小。并且We数越小，气泡成型时间的减小越接近线性变化。液滴间距越大，两液滴之间的低压区范围就越大，在压力梯度的作用下，液滴会更快地封闭弧形气室并形成气泡。图13给出了无量纲卷吸气泡尺寸随无量纲液滴间距的变化曲线图，可以看出无量纲液滴间距越大，液膜卷吸气体所形成的气泡尺寸就越大。

2.4 中心射流的破碎和影响因素

图14给出了不同We数下中心射流破碎发生的时刻，可以看出，随着We的增大，中心射流发生破碎的时刻明显提前。这是由于在相同的液滴间距与无量纲液膜厚度下，We数越大，液滴撞击液膜的速度就越快，生成的水花向内扩散发生碰撞融合的速度也越快，这就致使中心射流发生破碎的时间越早。

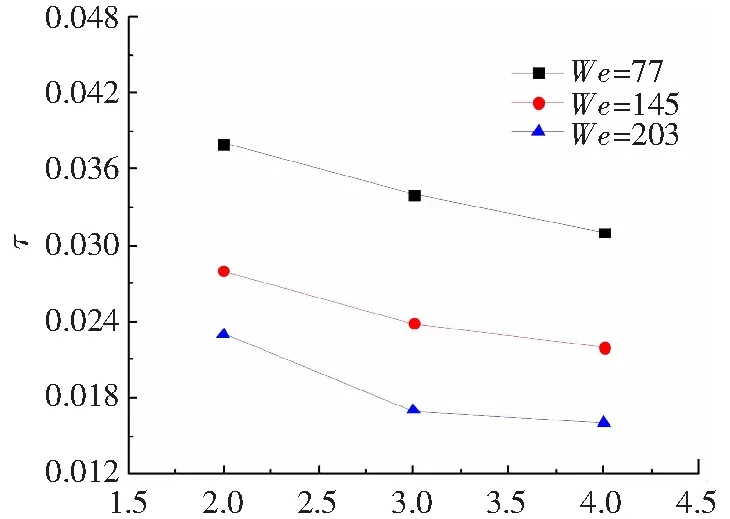
S*图12 气泡成型时间随无量纲液滴间距的变化曲线Fig.12 Variation of bubble forming time with dimensionless droplet spacing

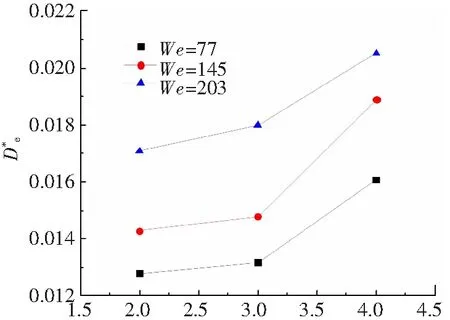
S*图13 无量纲气泡尺寸随无量纲液滴间距的变化曲线Fig.13 Variation of dimensionless bubble size with dimensionless droplet spacing

We图14 中心射流破碎时间随We数的变化曲线Fig.14 Variation of central jet breaking time with We

图15给出了不同液滴间距下，中心射流发生破碎时的We数阈值，可以得到，无量纲液滴间距越大，中心射流发生破碎现象的We数阈值就越小。液滴间距越大，向内侧发展的水花相融时顶部的液体向两侧发展的趋势更明显，中心射流也更容易发生破碎，因此当液滴间距增大时，中心射流在较小的We数情况下就能够发生破碎。中心射流发生破碎时We数的阈值随液滴间距的变化曲线将框图分为了两个区域，在曲线上的区域是中心射流能够发生破碎的区域，在曲线下的区域，则是中心射流不能发生破碎的区域。

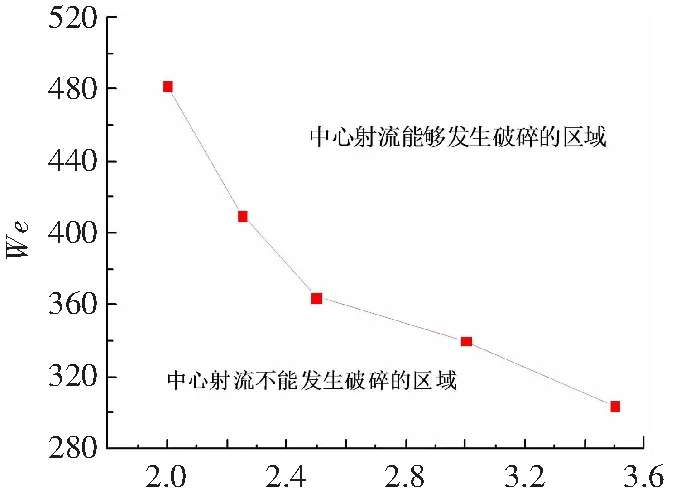
S*图15 不同无量纲液滴间距下中心射流发生破碎时We数的阈值Fig.15 Threshold value of We when the center jet is broken under different dimensionless droplet spacing

图16给出了无量纲液膜厚度δ分别为0.18,0.20和0.21时不同液滴间距下二次液滴成型时与中心撞击轴线的无量纲距离。由图可以看出随着无量纲液滴间距的增大，二次液滴成型时液滴越远离中心撞击轴线。这说明增大撞击时无量纲液滴间距，有利于液滴的飞溅，能够扩大液滴的分散范围。图17给出了二次液滴的无量纲体积随无量纲液滴间距变大的变化情况，可以看出无量纲液滴间距越大，形成的二次液滴体积越小。液滴之间的距离越远，水花向内传播就需要越多的时间，从而消耗更多的动能，导致破碎的水花只能形成较小的液滴。

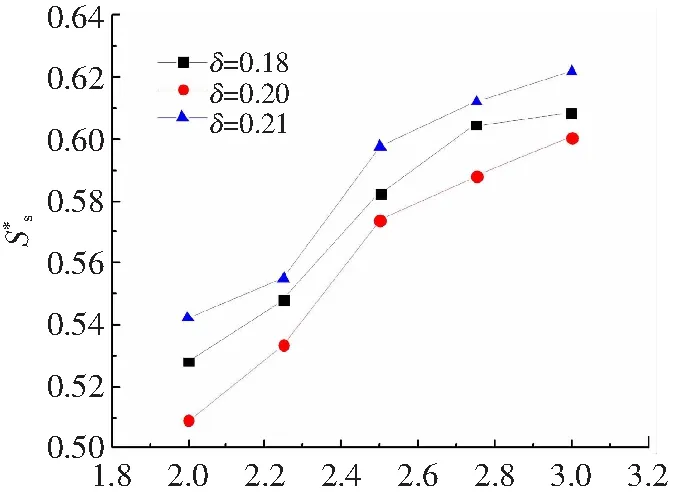
S*图16 不同无量纲液滴间距下二次液滴成型时与中心轴线的无量纲距离Fig.16 Dimensionless distance between the secondary droplet and the central axis when the secondary droplet is formed under different dimensionless droplet spacing

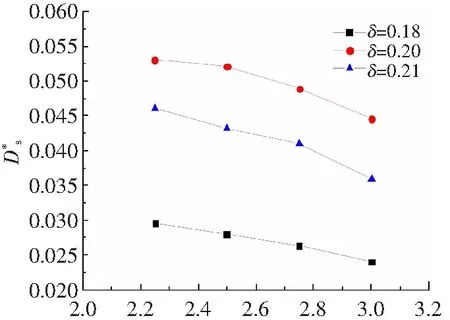
S*图17 不同无量纲液滴间距下二次液滴的无量纲大小Fig.17 Dimensionless size of secondary droplets under different dimensionless droplet spacing

3 结论

本文采用FTM方法研究了双液滴-液膜撞击系统产生的形态变化，讨论了双液滴-液膜撞击系统中中心射流的产生以及破碎，二次液滴的形成，液膜卷吸空气形成气泡等现象，并研究了不同参数对这些现象产生的影响。主要结论如下：

(1)We数越大，中心射流的发展速度就越快，中心射流能够达到更高的高度上限；更大的液滴间距，滞后了中心射流的出现时间，抑制了中心射流能够达到的最大高度。

(2)只有当We数在30～276的范围内，双液滴撞击液膜时才会出现液膜卷吸气体并形成气泡的现象；并且We数和无量纲液滴间距对气泡的生成都有促进作用，We数和无量纲液滴间距越大，气泡的成型时刻越早，形成的气泡体积也越大。

(3)在相同无量纲液膜厚度下，We数越大，液滴撞击液膜的速度就越快，中心射流就会越早发生破碎；液滴撞击液膜时的液滴间距越大，中心射流发生破碎时的We数阈值就越小；无量纲液滴间距越大，二次液滴成型时液滴距离中心撞击轴线越远，这有利于液体的飞溅扩散；但是液滴撞击时无量纲液滴间距越大，形成的二次液滴体积越小。